基于R-LWE的密文域多比特可逆信息隐藏算法
柯 彦 张敏情 苏婷婷
(网络与信息安全武警部队重点实验室(武警工程大学) 西安 710086) (武警工程大学电子技术系 西安 710086) (15114873390@163.com)
基于R-LWE的密文域多比特可逆信息隐藏算法
柯 彦 张敏情 苏婷婷
(网络与信息安全武警部队重点实验室(武警工程大学) 西安 710086) (武警工程大学电子技术系 西安 710086) (15114873390@163.com)
密文域可逆信息隐藏是一种以密文为载体进行信息嵌入与提取,同时能够对嵌入信息后的密文进行无失真解密并恢复出原始明文的信息隐藏技术,具有隐私保护与信息隐藏双重功能,在密文域数据处理与管理中具有较好的应用前景.因此,提出了一种基于R-LWE(ring-learning with errors)的密文域多比特可逆信息隐藏方案.首先使用R-LWE算法对载体明文进行快速高强度加密,然后通过对单位比特明文在密文空间映射区域的重量化以及对应密文的再编码,实现了在密文中嵌入多比特隐藏信息;嵌入信息时,根据加密过程中的数据分布特征来进行嵌入编码,保证了加解密与信息提取的鲁棒性;解密与提取信息时,先计算量化系数,而后采用不同的量化标准分别进行解密或信息提取,实现了解密与提取过程的可分离.分析方案的正确性时,首先推导方案出错的概率,说明了算法中引入的噪声的标准差对方案正确性的影响,然后结合理论分析与实验得出了保证方案正确性的噪声标准差的取值区间;通过推导嵌入后密文的分布函数,分析密文统计特征的变化,论证了密文中嵌入隐藏信息的不可感知性.实验结果表明:该文方案不仅能够实现嵌入后密文的无差错解密与秘密信息的可靠提取,并且单位比特明文在密文域能够负载多比特隐藏信息,密文嵌入率最高可达到0.2353 bpb.
信息安全;可逆信息隐藏;密文域;多比特嵌入;环上带误差的学习
传统的信息隐藏算法在嵌入过程中会给原始载体带来永久性失真,不能适用于嵌入信息后需要无失真恢复出原始载体的应用场合,如云环境下隐私数据标注、远程医学诊断、司法取证等对载体失真较为敏感的应用领域,因此可逆信息隐藏技术被提出,要求嵌入信息后可以无差错恢复出原始载体[1].随着网络的普及尤其是云服务的兴起,隐私保护与信息安全需求日益增强,数据往往以密文的形式进行传输与存储,因此面向密文载体的可逆信息隐藏技术受到广泛的关注.密文域可逆信息隐藏是指用于信息嵌入的载体是经过加密的,嵌入后仍然可以无差错解密并恢复出原始载体的一种信息隐藏技术,主要用于加密数据的管理与认证、加密域隐蔽通信[2]或其他安全保护.例如,远程医学诊断中为了保护患者隐私,通常加密传输或存储医学图像,同时为了对密文图像进行归类与管理,需要以可逆方式嵌入患者的私人信息甚至病历、诊断结果、病理图等隐私数据;云环境下,用户需要先对数据进行加密以确保云服务不泄露数据隐私,同时为了使云端或用户能够直接在密文域完成数据的检索或聚类,需要可逆嵌入一些额外的备注信息而不能影响用户解密原始数据;另外,在密文传输过程中,通过以可逆方式嵌入校验码或Hash值,可以实现不解密情况下数据的完整性与正确性检验等.综上,密文域可逆信息隐藏对于信息安全与隐私保护可以起到双重保险的作用,是当前密文域数据处理与信息隐藏技术的研究重点之一[3-4].
当前密文域可逆信息隐藏的技术难点主要在于实现秘密信息的大容量嵌入、载体数据恢复得完全可逆、信息提取与解密过程的可分离以及嵌入信息的不可检测性等方面.针对上述难点,该领域研究者们提出了多种解决方案,主要可分为部分加密和全局加密2类.部分加密算法是在加密前保留载体部分特征用于数据嵌入,而将载体剩余部分进行加密,如文献[5]是在压缩过程中利用部分DCT系数携带额外信息而将其余系数加密;文献[6]提出在H.264AVC格式视频的压缩过程中加密部分特征,而剩余部分特征用于数据嵌入;文献[7]利用树型哈尔变换域中的部分系数的位层实现信息嵌入.部分加密算法能够较好地保证载体恢复的可逆性与秘密信息的嵌入率,但是保留载体部分原始特征容易导致原始信息泄露,威胁载体信息安全,因此当前密文域可逆信息隐藏技术研究的重点在于全局加密类算法.
全局加密算法是对载体信息全部加密,数据嵌入过程完全在密文域上进行,不会造成原始信息泄露.全局加密算法中的一类算法是通过引入密文域信息处理技术实现密文域嵌入,如同态技术[8-9]与熵编码[10]等.文献[8-9]用公钥密码加密载体数据,利用同态加密嵌入信息,能够在密文域直接进行操作实现嵌入,具有良好的可逆性;文献[2]利用双层嵌入的方法在明文数据中嵌入信息,并设计了一种修正的全同态加密算法对载密数据进行加密,最后在密文域上提取隐藏信息,该算法能够可分离地进行载密数据解密与隐藏信息提取,并且在密文域同态嵌入的基础上进一步引入密码学中可证明安全理论论证了所提方案的安全性.但是上述文献中引入全同态加密后造成算法的计算复杂度过大,执行效率与秘密信息嵌入率较低.文献[10]引入熵编码技术在密文编码过程中嵌入信息,能够达到完全可逆,执行效率与嵌入率有了很大提高,但是由于算法的可逆性是基于解码过程的可逆性,因此解密与信息提取过程不可分离.而当前全局加密的另一类重要算法主要是基于图像处理与加密、密文数据压缩等技术来实现密文域嵌入,该类算法计算复杂度较小、执行效率较高:文献[1]首次将图像加密技术和信息隐藏结合一体,提出密文图像中的可逆信息隐藏算法,操作简单且满足一定的可逆性要求,但是信息提取需要先进行图像解密,隐写荷载与可逆恢复质量受加密算法与图像内容限制较大;在此基础上,文献[11]通过改进失真函数提升了这种方案的可逆性能,而文献[12-13]通过改进嵌入技术进一步提高了嵌入容量,但是嵌入量提高后的载体图片解密失真会有所增大;之后文献[14]提出在加密的JPEG比特流中嵌入可逆信息以及文献[15]提出基于邻域像素平均差值的密文域可逆信息隐藏算法对文献[1]进行改进,但仍然存在嵌入容量与可逆性相互制约的问题;文献[16]引入随机扩散的方法有效利用了文献[1]中的像素空域关联性,通过设计精确预测的算法在降低解密差错的同时提高了嵌入容量.但是上述算法[1,11-16]均不能实现载体解密恢复与信息提取过程的可分离,为此,文献[17]提出可分离的加密图像隐藏算法,利用矩阵运算的方法把加密的图像的 LSB 进行压缩腾出空间嵌入信息,在接收方分3种情况:使用隐藏密钥可以提取嵌入数据、使用解密密钥可以对携秘密文图像直接解密,2个操作可以单独执行;同时使用隐隐藏密钥与解密密钥可基本实现载体的完全恢复.文献[17]的方案操作简单,适用于更多的应用场景,但是图像载体恢复是基于像素间相关性,因此使用解密密钥直接对携秘密文解密时,由于可参考的像素点有限,造成解密存在一定失真;文献[18]使用压缩传感的方法实现了解密与信息提取可分离,将加密后图像与隐藏信息2部分数据压缩成原始密文图片的大小,压缩过程即完成了密文域额外信息的嵌入,解密与信息提取过程可分别在解压后独立进行,能够较好地保证载体恢复的可逆性,但是嵌入量受密文内容与压缩方式限制,而且解密恢复与提取过程都依赖于无损解压,因此解密过程会导致隐藏信息暴露.此外,现有的密文域可逆信息隐藏算法在安全性,即保证密文嵌入前后统计特征不变与嵌入数据的不可感知性方面的相关研究还比较少.
通过上述分析可知,构造完全可逆、高嵌入率且解密与信息提取可分离的密文域可逆嵌入算法是该领域研究与技术应用的重点.而当前全局加密类算法使用的加密系统多数为对称密码系统,与公钥密码系统相比,对称密码密钥生成与管理难度大,适用的加密场景有限,为此文献[19]提出基于格上的LWE(learning with errors)公钥加密的可逆隐写方案,在可逆性、可分离性、执行效率与隐写安全性方面都有着较好的保证.本文主要针对文献[19]进行嵌入过程编码算法的优化,以及执行效率与嵌入量上的改进.
在文献[19]中,首先对LWE算法加密过程中引入噪声的标准差进行约束来产生可控冗余,然后对密文进行再编码实现在密文的可控冗余中嵌入额外数据,1 b明文在密文域可最大负载1 b秘密信息,解密恢复与信息提取的正确性基本达到了100%,并且在信息提取与解密过程中使用不同的量化标准实现了解密与信息提取的可分离.但是当明文长度增加时,为保证加密安全性,密钥长度也相应增长,造成密文扩展率较高.设格空间向量长度为m,文献[19]中一次可加密与嵌入的数据长度为O(m),安全密钥长度为O(m2),1 b明文对应密文域空间为O(m2),因此文献[19]的加密与嵌入方案依然存在大量的计算冗余与空间冗余可用于提高信息嵌入效率.由此,本文基于文献[19]的算法进行3方面的改进:
1) 对加密与嵌入的执行效率进行改进,引入环上更高效的环上带误差的学习(ring-learning with errors, R-LWE)[20]加密算法,设环上多项式向量维数为m,多项式长度为n,在与文献[19]相同时间复杂度与加密强度的情况下本文方案一次可加密与嵌入的数据长度为O(mn),由于R-LWE算法[20]中没有详细给出R-LWE加密系统的参数取值,本文结合理论分析与实验仿真对方案中加密与嵌入过程的参数取值进行了详细地讨论说明;
2) 文献[19]中要求加密过程对噪声标准差进行约束来控制噪声波动规模以保证方案的正确性,本文通过改进嵌入编码方式,充分利用噪声的原始分布进行重新编码来嵌入额外信息而不需要对噪声分布标准差进行额外的约束,有效保证了原始加密的鲁棒性与方案的正确性;
3) 通过对密文域进行重量化,并划分子区域,可对应嵌入多进制数据构成的秘密信息,当秘密信息为B进制数据时,1 b明文在密文域最大可负载logBb额外信息.实验结果表明与文献[19]相比,本文在运行效率提高、计算复杂度不变的前提下,信息嵌入量提升到1 b明文,在密文域可负载4~8 b秘密信息.
最后,本文在安全性分析中通过理论分析与仿真实验结果说明了方案嵌入后的密文服从均匀分布,符合传统加密数据的统计分布特性.
1 相关技术
1.1 (R)LWE问题与分析
2005年,Regev首次提出了LWE问题[21].其复杂性可以归约到格上的判定性最短向量问题(gap version of shortest vectors problem, GAP-SVP)和最短无关向量问题(shortest linearly independent vectors problem, SIVP)[22],上述2种格中困难问题已经被证明是NP困难的,而LWE问题可以看作随机线性码的解码问题,或者格上的有限距离解码问题(bounded distance decoding problem, BDD),其困难性可以归约到标准格中困难问题的最困难情况[23].而且已知求解LWE问题的算法都运行在指数时间内,能够抵抗量子攻击,因此LWE问题具有可靠的理论安全性.此外,各类媒体的数据量极大,而格是一种线性结构,LWE算法中的运算基本都是线性运算,加密速度比目前广泛使用的基于大整数分解难题和离散对数难题的公钥密码高出很多,可以很好地适用于媒体数据量极大的云环境.但是随着格空间向量长度m的增大,为保证加密安全性, LWE算法需要相当大的密钥长度,通常是m2阶,并且方案密文数据的扩展与计算复杂度也随之增大,实用性降低.2007年,Kawachi等人针对Regev等人的LWE算法,提出格上的多比特加密算法[24],通过约束[21]等算法中噪声分布的标准差,使密文域中可容纳的噪声有效波动区间数从2个增加到2n个,实现明文可一次加密位数为O(lbn),但是与原LWE算法相比,文献[24]损失了一定的加密安全性与加解密鲁棒性.2010年,Lyubashevsky等人提出LWE环上的代数变种R-LWE[20],并证明其困难性也可以归约到标准格中困难问题的最困难情况,与Regev与Kawachi等人的算法相比,Lyubashevsky的R-LWE算法通过运算结构的改进,在保持加密强度与加解密鲁棒性不变的情况下加密效率更高,密钥长度更小.
Lyubashevsky的R-LWE算法可有效应用于密文域可逆信息隐藏,因为R-LWE算法加密后的数据扩展携带大量信息冗余,该部分冗余对于没有私钥的攻击者来说不包含任何有用信息,但是对于拥有私钥的用户来说可嵌入隐藏信息.本文主要工作为在数据加密与嵌入前的预处理过程中,通过引入流密码进行随机置乱,保持了嵌入前后R-LWE算法加密的困难性;通过对1位二进制明文在密文空间映射区域的重量化与对应密文的再编码来嵌入1位多进制数据,实现了单位比特明文可在密文域负载多比特隐藏信息;通过在密文域重量化过程中划分子区域,并根据加密过程中的数据分布进行再编码保证了加解密过程的鲁棒性,而对影响R-LWE算法加解密正确性的各关键参数(如噪声标准差)没有额外的约束,保证了嵌入后密文的无差错解密与嵌入信息的可靠提取;最后,在解密与信息提取过程中,分别采用不同的量化标准实现了提取与解密过程的可分离.
文献[24]是当前基于格进行多比特加密的代表算法,通过控制噪声标准差缩小噪声波动区间,使原算法中1 b明文对应的密文空间可容纳多个噪声波动,从而满足多比特明文在一次加密过程中可以映射在不同的噪声波动区间,实现一次加密多比特明文,但是对噪声标准差的约束会直接造成LWE算法的加密强度与加解密鲁棒性降低.而本方案主要通过对密文域空间的重量化与密文数据的再编码实现多比特信息嵌入,嵌入编码根据加密过程中的数据分布进行,对加密过程中引入噪声的标准差没有额外约束,充分保证了原R-LWE算法的加密强度与鲁棒性,本文在第3节具体分析了算法的正确性与安全性.最后,本文方案是在载体数据按比特位加密的过程中嵌入信息,与载体种类无关,适用于文本、图片、音频等载体.
1.2 Lyubashevsky的R-LWE加密算法[20]
Lyubashevsky的R-LWE算法是格上基于R-LWE问题的经典公钥密码算法,本节介绍R-LWE算法过程,并对算法正确性进行说明.
设多项式向量维数d=O(lbq),f(x)=xn+1,q>2n2,多项式环Rq=q[x]〈f(x)〉,r∈q.
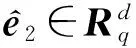

结合图示对上述算法的正确性进行简要说明:
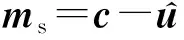

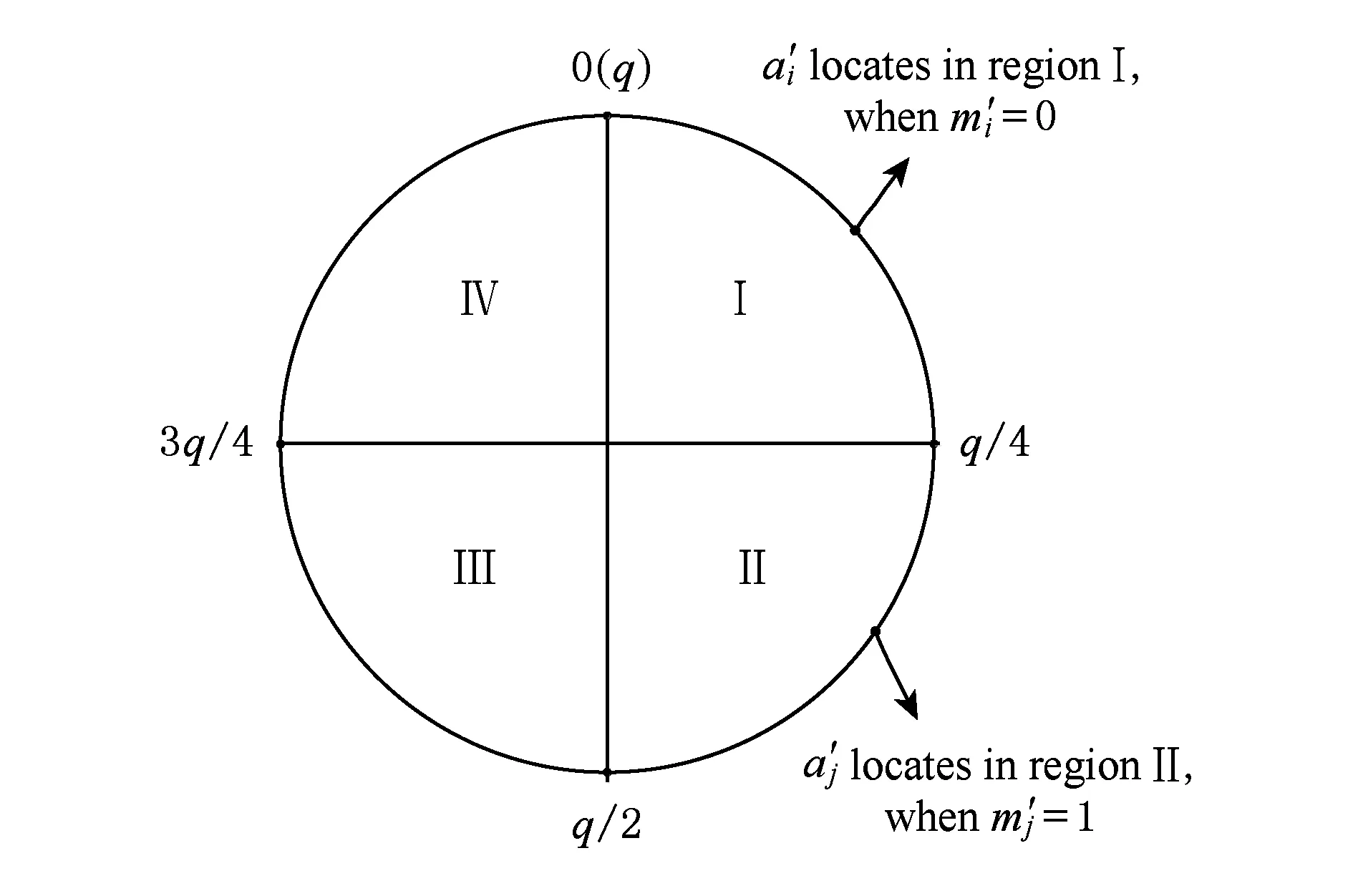
Fig. 1 The distribution of integers in q.图1 整数域q的取值分布
2 本文算法介绍
2.1 设计思想

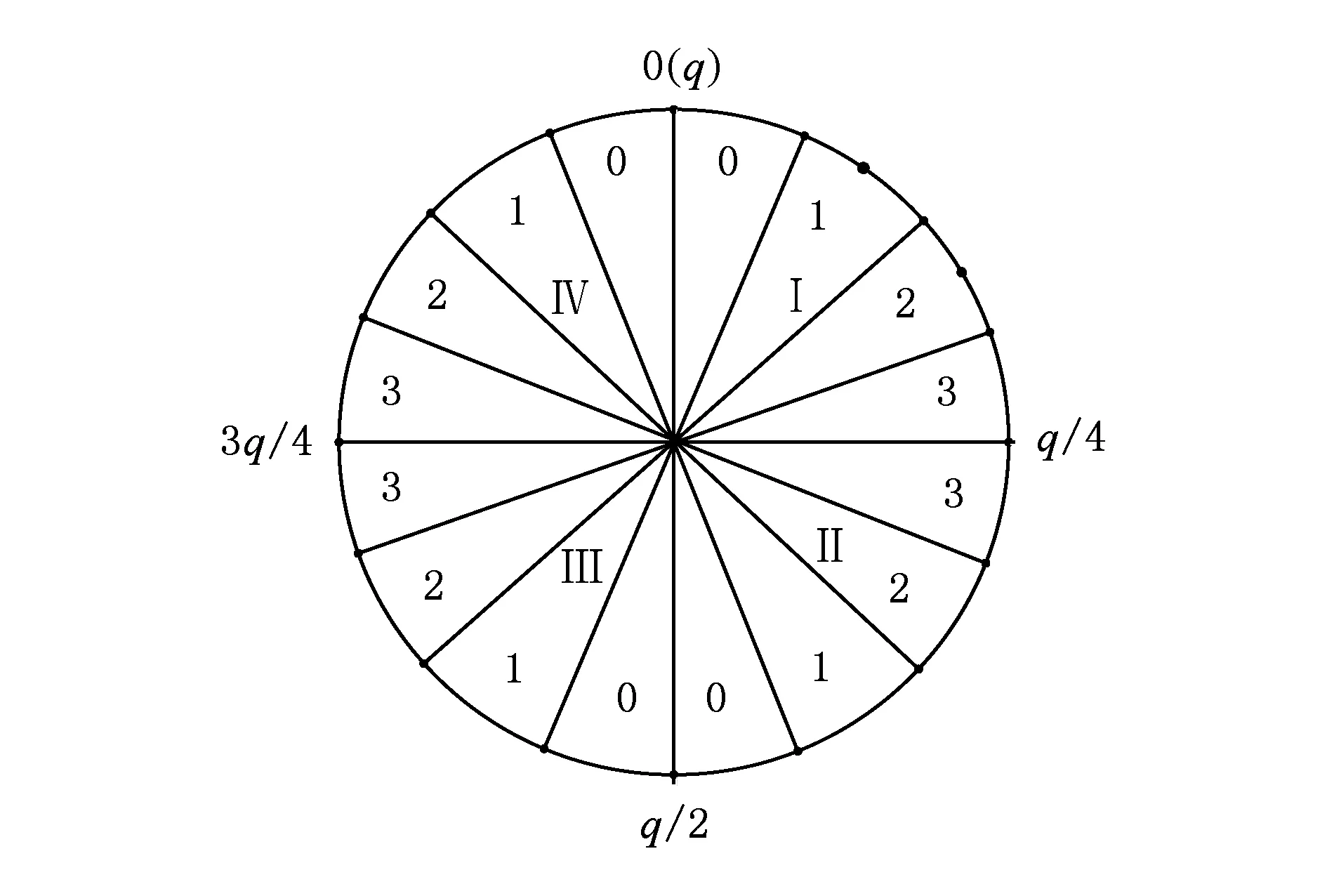
Fig. 2 The partition of integers in q.图2 整数域q的区域划分
算法主要包括参数设置、数据预处理、加密并嵌入数据、数据解密与信息提取等过程.图3为算法的系统架构与流程框架,图3(a)中随机序列作为用户私钥的一部分,用于预处理及解密或数据提取后的信息恢复,因此通常要求与系统参数及加密公私钥一同更新.由图3系统架构可见,算法主要应用于公钥加密系统下的秘密通信双方,隐藏密钥的持有者才能进行密文域的嵌入提取及密文管理.如果通信双方以外的可信第三方(如云服务器端)要进行数据嵌入与提取,可以通过事先协商系统参数并相应调整密钥(隐藏密钥与解密密钥)的分配策略来实现.

Fig. 3 Brief framework of proposed scheme.图3 算法框架示意
算法过程中使用函数L来返回输入值x所在子区域的编号.
定义1. 函数L:y=L(x),y∈{0,1,…,B-1},
x∈q,表示q中元素x位于子区域y.则:
(1)
下面详细介绍算法过程.
2.2 本文算法过程
2.2.1 参数设置
选取安全参数k>1、模数q,构造多项式环Rq=q[x]〈f(x)〉,生成多项式f(x)=xn+1,n=2k,所有运算在多项式环Rq上进行.多项式向量维数d=O(lbq),噪声的分布为χ,其中α=1poly(n);
2.2.2 数据预处理
设明文信息为p∈{0,1}n,隐藏信息为二进制序列mh.将p与随机二进制序列r1异或生成用于加密的序列s1=[m0,m1,m2,…,mn-1],mi∈{0,1};mh与随机二进制序列r2异或得到序列s2:
s1=r1⊕p,
(2)
s2=r2⊕mh,
(3)
将s1编码为系数为二进制数的环多项式m用于加密,m=m0+m1x+…+mn-1xn-1,mi∈{0,1};将s2编码为系数为B进制数的环多项式w用于嵌入,w=w0+w1x+…+wn-1xn-1,wi∈{0,1,2,…,B-1}.
2.2.3 加密与信息嵌入
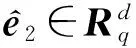

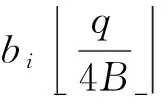
(4)
其中,
(5)
bi=wi-L(hi),
(6)
βibi∈{-1,1},其符号决定嵌入过程中密文ci改变的正负;bi∈{-B+1,-B+2,…,-1,0,1,…,B-1},bi的绝对值表示嵌入过程中原始密文ci偏移|bi|个量化步长.
2.2.4 解密与信息提取
(7)
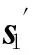
(8)

(9)
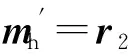
(10)
3 算法分析与仿真实验
3.1 正确性分析

Fig. 4 The distribution of integers in q.图4 整数域 q 的取值分布
方案的正确性主要包括嵌入后密文的正确解密与嵌入信息的正确提取2方面.本节首先分析影响方案正确性的相关参数.
完成上述加密与嵌入过程后,用户即可实现可分离的解密得到原始明文或提取隐藏信息:
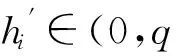
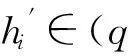
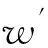
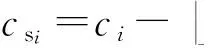
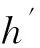
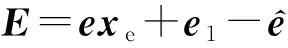
(11)
则方案出错的概率为
P(|Ei|>q4)=Pr(|Ei|σ>q4σ)≤
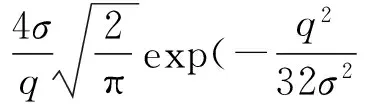
(12)
由式(12)可知,当标准差α足够小时σ越小,噪声产生的波动Ei较小,方案出错的概率接近于0.在LWE算法中α通常取O(1lbn)[23].另一方面LWER-LWE问题求解的困难性依赖于噪声的存在,如果α太小,噪声分布在均值0附近偏差很小,噪声波动区间的过小影响方案的安全性.为了保证加密强度,引入噪声的波动范围要足够大,R-LWE算法中通常要求lbn[20].因此系统参数确定的情况下,噪声分布的标准差对方案的正确性与安全性起着关键作用.文献[20]中算法通过理论证明了R-LWE算法的安全性与正确性,但是关于相关参数对方案性能的影响只是进行了理论上的分析,在实用过程中的各关键参数的取值范围并未具体说明,本文在参考理论分析的基础上通过对大量数据进行加密与信息隐藏测试,进一步确定不同加密情况下噪声分布标准差α的合理取值.
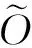
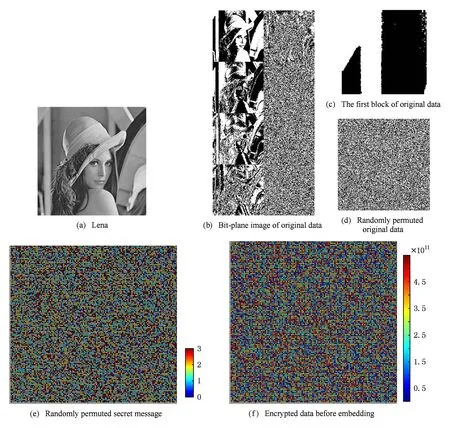
为直观反应实验结果,以k=11,B=4,n=211加密Lena图像的前214b数据并嵌入216b信息,检验标准差α=8.204 2×10-6时方案的正确性为例来介绍实验过程.结合图5对实验过程进行说明如下:

Fig. 5 Experiment the image Lena by the proposed scheme with k=11,B=4,n=211.图5 本文算法对Lena图像的实验过程(k=11,B=4,n=211)
其中图5(a)为实验载体图像Lena;按位平面分离为二值序列得到位分离图5(b);将位分离图分为128×128的互不重叠的二值数据块,选取其中第1个块作为明文数据进行加密,明文用二值图像表示如图5(c);将明文随机置乱如图5(d);随机选取4进制数据作为隐藏信息如图5(e);加密后的原始密文如图5(f);对原始密文进行嵌入得到携秘密文如图5(g);直接从携秘密文中提取到的隐藏信息如图5(h);直接将携秘密文进行解密并逆置乱得到解密结果如图5(i);通过逐比特位作差法分别对比解密数据与明文数据、秘密信息与提取信息结果如图5(j),表明解密与提取信息无差错;将图像Lena的位分离图中剩余数据块重复上述过程(当明文数据长度小于n时,填充0或1),得到完整的位分离图,按位填充于各像素,最终恢复得到实验图像如图5(k).表明实验中所选的α=8.204 2×10-6满足系统参数k=11时密文的正确解密与秘密信息的正确提取,正确率基本达到100%.
重复进行加密与信息隐藏测试,记录标准差可取值的上限αmax.表1为实验得到的保证方案正确性的标准差上限值αmax及满足加密安全需要的下限值αmin.根据αmax与αmin得到α取值区间[λ αmin, ν αmax](λ>1,ν<1).根据该区间继续对标准测试图片、文本、音频等数字载体进行实验,结果表明:α在该区间取值可有效保证方案的正确性,其解密与提取隐藏信息的正确率基本达到100%.
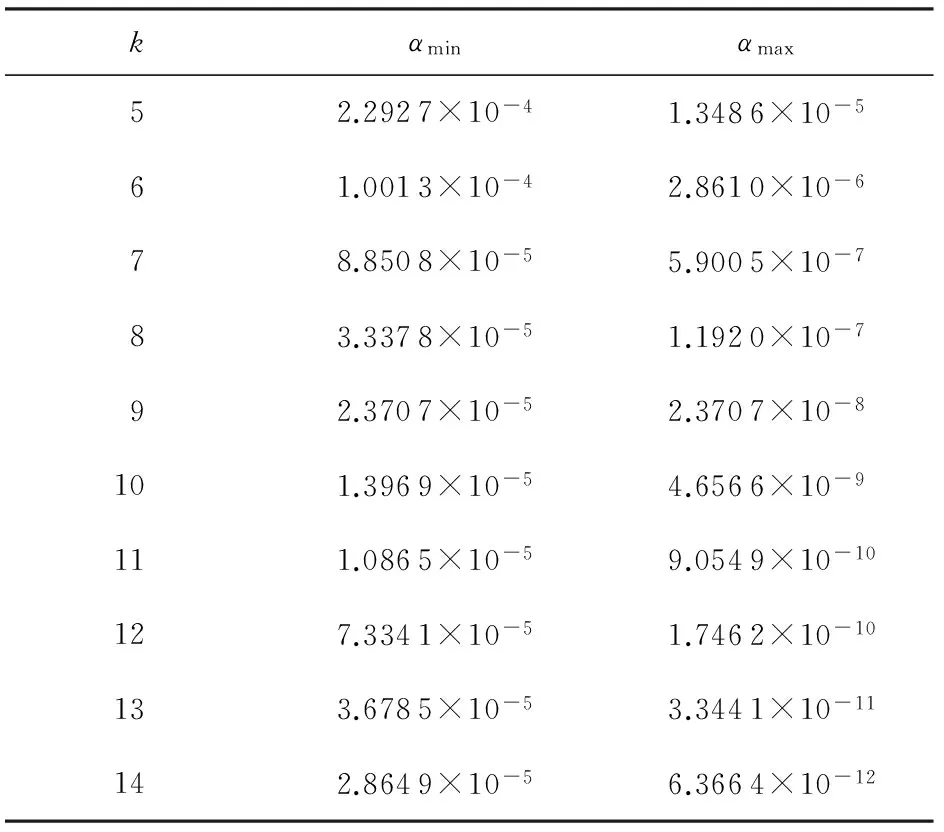
Table 1 Ranges (αmin,αmax) of α with k∈[5,14]
可逆隐写算法的评价标准中峰值信噪比(peak signal-noise ratio,PSNR)用来评价与原始载体信息相比较,恢复后载体的质量或失真情况.PSNR值越大,表示图像失真越小.对于大小M×N的256级灰度图像PSNR:
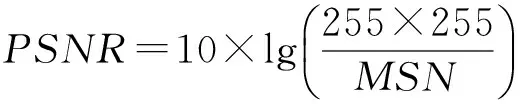
(13)
其中,MSE表示恢复图像像素矩阵I′与原始图像像素矩阵I的均方误差(mean squared error,MSE):
(14)
一般,当PSNR>35 dB时,人眼视觉就无法感知图像的失真[26].图6为使用密文域可逆信息隐藏算法[1]及可分离算法[17]对标准图像库中图像Lena,Man,Lake,Baboon进行实验得到的直接解密恢复图像的PSNR.
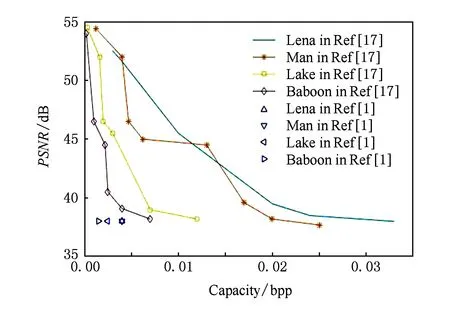
Fig. 6 PSNR comparison of the methods in Ref [1,17].图6 文献[1,17]中算法载体直接恢复的PSNR
PSNR取值基本在35 dB~60 dB,与当前大多数算法的可逆恢复效果相近,表明数据嵌入会在直接解密得到的图像中引入失真,只是将失真控制在人眼无法感知的程度,且嵌入量越大失真越大.而本文算法解密恢复的正确率基本保持在100%,将解密结果代入式(13)(14)得到直接解密恢复图像的PSNR值如表2所示,说明可完全保证可逆性.
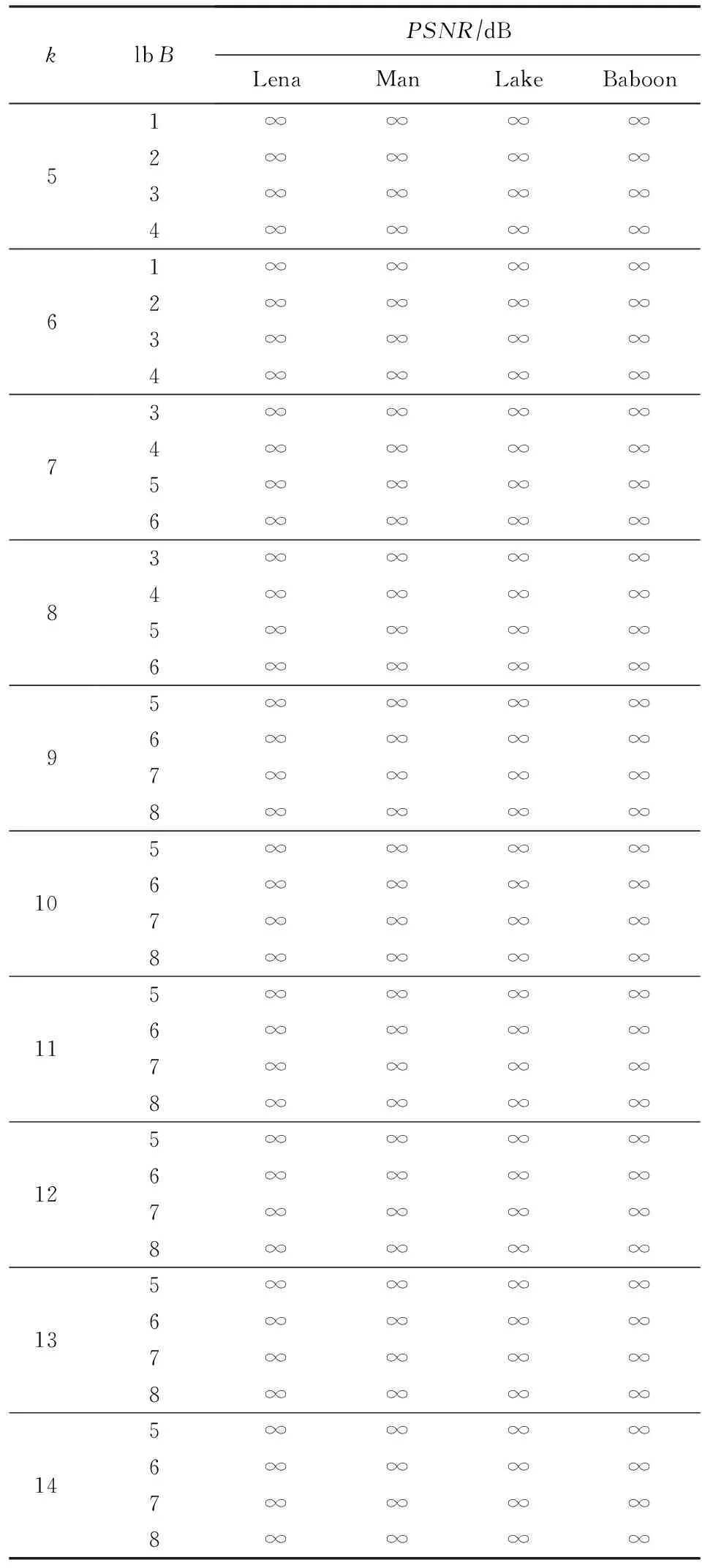
Table 2 PSNR of the Proposed Scheme
3.2 安全性分析
密文域可逆信息隐藏的安全性主要是保持加密的安全性与嵌入信息的不可感知性2方面,其中不可感知性是可逆隐写算法的重要评价指标与实现密文域隐蔽通信的重要保证[2,19].在保持加密安全性方面,图像加密及公钥密码算法安全性的关键指标之一是加密数据符合均匀分布[27],因此为保证嵌入过程不造成加密信息泄露,嵌入后的密文数据也应服从均匀分布;在不可感知性方面,相关的研究还比较少,现有算法主要是分析载体嵌入信息前后的峰值信噪比(PSNR),即嵌入前后载体数据的改变量.但是对于密文来说,因为公钥加密算法要求明文的极小改变也将扩散到整个密文空间,嵌入前后的PSNR不能有效说明密文数据的变化是由于明文不同还是嵌入了额外信息,而且隐写分析技术在对密文进行隐写分析时通常不能获得原始密文,当前主要是对载体数据进行概率统计上的分析建模、提取特征,通过对特征分类来判断是否隐藏信息[28],因此对于密文域隐写的安全性,不能简单通过嵌入前后密文数据的改变量来说明,而是要求保持嵌入前后密文数据统计特性不变[19].综上,本文在安全性分析中,着重分析密文在嵌入后的分布函数与统计特征.首先,推导嵌入后密文的分布函数如下:
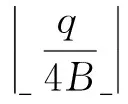
P[Ei∈(0,q4)]=Fσ(0)=
P[Ei∈(3q4,q)]=1-Fσ(0)=12.
(15)
又当Ei∈(0,q4)时,qq3q),βi=1;
当Ei∈(3q4,q)时,qq3q,q),βi=-1.
故:
P(βi=1)=P(βi=-1)=12.
(16)
函数L(e)∈{0,1,…B-1},e∈q,表示q中元素e所在的子区域,记将正态分布下函数L值为y时的概率为PL(y).则可得:
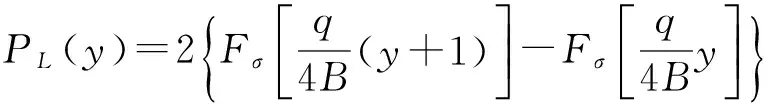
y∈{0,1,…,B-1}.
(17)
方案中秘密信息多项式w的系数经随机置乱,则:
P(wi=0)=P(wi=1)=…=
P(wi=B-1)=1B,
(18)
又bi=wi-L(hi),bi∈{-B+1,-B+2,…,0,…,B-1},wi,L(hi)∈{0,1,…,B-1},记bi取值为x时的概率为Pb(x),根据离散卷积公式得到bi的分布律如下,表3具体列举了bi取不同值时各变量的取值情况及其分布律:

Table 3 Distribution Ratio of bi
由上可推得隐写前后密文产生不同改变量时的概率,
P(βi=-1)Pb(-λ),
(19)
P(βi=1)Pb(-λ),
(20)
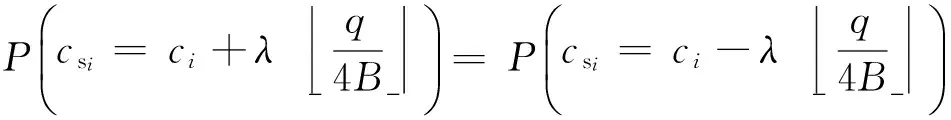

Table 4 Distribution Ratio of λ
设原始密文ci~U(0,q),其分布函数符合均匀分布,记为Fc(x)=xq,x∈(0,q),嵌入后密文的分布函数记为Fcs(x):
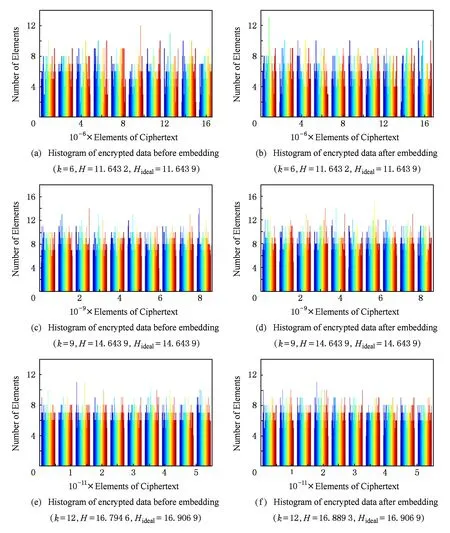
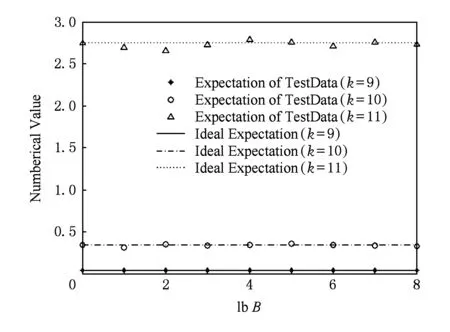
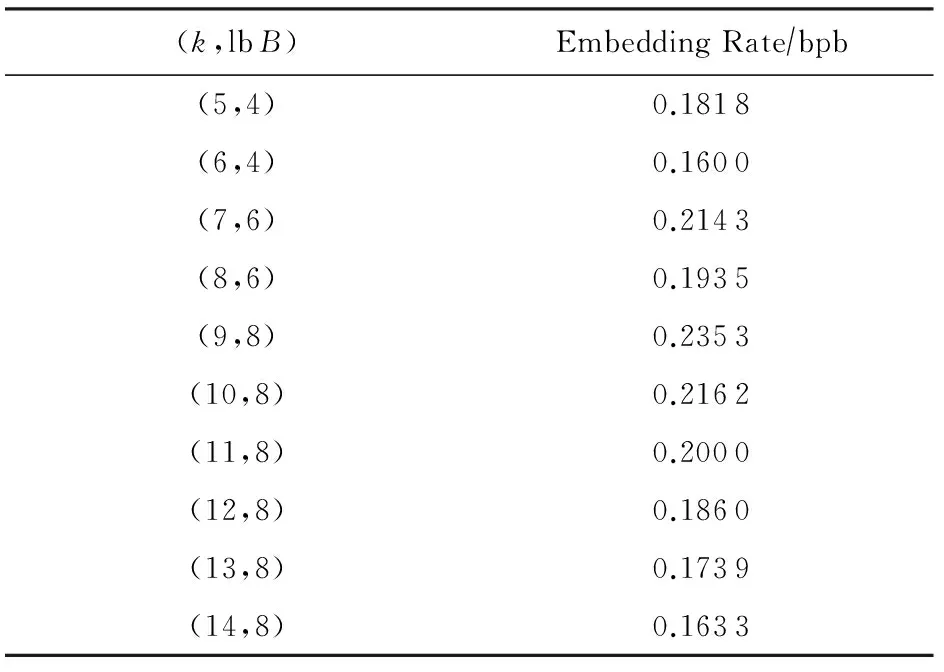
Fcs(x)=P(csi (21) 由式(21)可知,嵌入信息后密文数据的分布函数与原始密文分布函数一致,服从q上的均匀分布. 下面通过实验分析说明嵌入信息后密文的统计特征.实验参数设置如下:k=6,9,12,q=64n3+1,n=2k,B=8;参数d,r影响方案的密钥安全,根据剩余Hash引理[25],保证公钥接近均匀分布的一个充分条件就是私钥的取值空间要远远大于公钥的取值空间,即(r+1)d n≫qn,又因为d越大密文扩展率越大,公钥长度也成倍增加,在满足安全性的前提下,为节省公钥存储空间,取d=lbq,r=64.α从3.1节得到的区间取值:α∈[λαmin,ναmax](λ>1,ν<1).对多组大量样本数据进行加密,1 b明文在加密域携带3 b数据,如图7所示嵌入前后密文分布直方图,图7中颜色渐变用于区分不同组的样本数据.计算各组样本实验结果的信息熵,记为H,对应加密域中元素等概率分布时的最大信息熵记为Hideal,结果如图7所示. 由图7可以看出信息嵌入后密文直方图没有出现明显变化,而且嵌入过程的再编码相当于对密文进行粗粒度的随机置乱,因此对密文数据直方图的分布特性基本不会发生破坏.B取其他值进行实验,结论与上述一致.对上述直方图中数据计算平均信息熵,结果表明嵌入后密文数据的信息熵不低于原始密文,基本接近于加密域中元素等概率分布时的最大信息熵. Fig. 7 Histograms and information entropy of encrypted data before embedding and those after embedding.图7 信息隐藏前后密文数据分布直方图与平均信息熵值 Fig. 8 Relationship between expectation of test data and ideal expectation.图8 不同嵌入量下密文期望与理想期望关系 由实验结果可见:在误差允许范围内,不同嵌入量下的密文数据期望与所在密文域的理想期望基本一致,表明在嵌入信息后密文的统计期望未发生明显变化. 3.3 嵌入容量分析 在嵌入容量方面,文献[17]中载荷约为0.0328 bpp,即8 b大小的像素可嵌入0.0328 b信息;文献[13]通过翻转第6LSB位的方式实现了载荷的有效提升,约0.06 bpp;文献[29]将LDPC编码引入密文域可逆隐写,将载荷提升到0.1 bpp.已有针对于图像载体的密文域可逆信息隐藏算法的嵌入率受到像素内容或加密方式的限制较大,有效载荷基本不超过0.5 bpp,文献[10]使用熵编码实现通用密文域可逆信息隐藏,在完全可逆的情况下嵌入量基本达到0.169 bpb,即1 b密文可携带0.169 b秘密信息;文献[19]在LWE算法加密后数据的冗余部分嵌入信息, 1 b明文在密文域最大可负载1 b隐藏信息.与文献[19]相比,本文方案当选择B进制数作为秘密信息时,1 b明文在密文域最大可负载lbBb隐藏信息,本文方案的密文嵌入率的情况具体分析如下. Fig. 9 Embedding rates in different settings of proposed scheme.图9 不同系统设置下的密文嵌入率 如图9所示为根据表3中实验结果得出在不同的安全参数k的取值时,单位比特密文的嵌入率随lbB取值变化的情况.结合3.1节、3.2节分析与图9可知,系统安全参数k不变时,嵌入率随lbB增大而提高;lbB不变时,k越大加密强度越大,一次可加密的明文与嵌入信息量增多,但密文扩展较大,嵌入率降低.因此在实际应用中可根据加密与信息嵌入的现实需要选择合适的安全参数k与嵌入信息进制数B.但是参数B不能无限增大,原因是随着B值的增大,方案中q划分子区域的量化步长q不断缩小,造成嵌入过程对加密数据的修改粒度越细,由3.2节中分析可知算法安全性依赖于预处理过程中嵌入数据的随机性,因此预处理过程中随机数生成器的安全性对加密数据的影响随着量化步长的缩小而加强.如果随机数生成器生成数据的随机性低于R-LWE算法加密结果的随机性,随着B的增大,量化步长小于安全性需要的噪声波动的最小值时,嵌入后密文数据的安全性会降低.而高强度的随机数生成器会影响方案的执行效率,综合考虑当前随机数生成算法的安全性与运行效率,B的取值不能无限取大. 本文实验中相关参数的选择充分保证了量化步长大于噪声波动的安全性需要的下限,如表5所示为不同系统设置时的密文最大嵌入率,表5中第1列表项(k,lbB)列举了嵌入率最大时的系统安全参数k与秘密信息的进制数B. Table 5 Hightest Embedding Rates in Different Settings of Proposed Scheme / bit per bit of ciphertext 表5 不同系统设置下单位密文最大嵌入率/bpb 根据实验结果,密文嵌入率可达到0.1600 bpb以上,其中k=6,lbB=4时密文嵌入率最小,为0.1600 bpb;当k>9时,1 b明文在密文域可最大负载8 b秘密信息,其中k=9,lbB=8时单位密文的最大嵌入率达到0.2353 bpb,此时方案的加密执行效率与嵌入率达到最理想状态. 本文提出了基于R-LWE的密文域多比特可逆信息隐藏算法,通过对密文域的分区量化以及加密数据的重编码来嵌入多比特额外信息,提高信息嵌入率的同时保证了携秘密文的可逆解密与嵌入信息的无失真提取.理论分析与仿真实验说明了方案的正确性、安全性以及在嵌入容量上的有效保证.当前基于(R-)LWE的公钥加密算法广泛用于构造多种应用场景下的密码方案,如数字签名、属性加密,满足可信第三方密文处理的代理重加密[30]、全同态加密[31]等,未来可将本方案的嵌入技术应用于上述基于(R-)LWE的加密环境与密码应用中,进一步扩展密文域可逆信息隐藏的应用场景.但是本方案随着算法加密规模的增大,算法的密文扩展仍然较大,未来工作需要进一步精确嵌入容量的有效范围,改进信息嵌入的编码方式来更好地利用密文扩展,提高密文域隐藏信息的嵌入率. [1]Zhang Xinpeng. Reversible data hiding in encrypted image[J]. IEEE Signal Processing Letters, 2011, 18(4): 255-258 [2]Chen Jiayong, Wang Chao, Zhang Weiming, et al. A secure image steganographic method in encrypted domain[J]. Journal of Electronics & Information Technology, 2012, 34(7): 1721-1726 (in Chinese)(陈嘉勇, 王 超, 张卫明, 等. 安全的密文域图像隐写术[J]. 电子与信息学报, 2012, 34(7): 1721-1726) [3]Yin Zhaoxia. Privacy protection oriented image steganography[D]. Hefei: Anhui University, 2014 (in Chinese)(殷赵霞. 面向隐私保护的数字图像隐写方法研究[D]. 合肥: 安徽大学, 2014) [4]Barni M, Kalker T, Katzenbeisser S. Inspiring new research in the field of signal processing in the encrypted domain[J]. IEEE Signal Processing Magazine, 2013, 30(2): 16 [5]Zhao Bin, Kou Weidong, Li Hui, et al. Effective watermarking scheme in the encrypted domain for buyer-seller watermarking protocol[J]. Information Sciences, 2010, 180(23): 4672-4684 [6]Lian Shiguo, Liu Zhongxuan, Ren Zhen, et al. Commutative encryption and watermarking in video compression[J]. IEEE Trans on Circuits and Systems for Video Technology, 2007, 17(6): 774-778 [7]Cancellaro M, Battisti F, Carli M, et al. A commutative digital image watermarking and encryption method in the tree structured Haartransform domain[J]. Signal Processing: Image Communication, 2011, 26(1): 1-12 [8]Kuribayashi M, Tanaka H. Fingerprinting protocol for images based on additive homomorphic property[J]. IEEE Trans on Image Processing, 2005, 14(12): 2129-2139 9]Memon N, Wong P. A buyer-seller watermarking protocol[J]. IEEE Trans on Image Processing, 2001, 10(4): 643-649 [10]Abdul Karim M S, Wong K. Universal data embedding in encrypted domain[J]. Signal Processing, 2014, 94(2): 174-182 [11]Hong Wien, Chen Tungshou, Wu Hanyan. An improved reversible data hiding in encrypted images using side match[J]. IEEE Signal Processing Letters, 2012, 19(4): 199-202 [12]Yu Jie, Zhu Guopu, Li Xiaolong, et al. Digital Forensics and Watermarking: An Improved Algorithm for Reversible Data Hiding in Encrypted Image[M]. Berlin: Springer, 2014: 384-394 [13]Wu Xiaotian, Sun Wei. High-capacity reversible data hiding in encrypted images by prediction error[J]. Signal Processing, 2014, 104(11): 387-400 [14]Qian Zhenxing, Zhang Xinpeng, Wang Shuozhong. Reversible data hiding in encrypted JPEG bitstream[J]. IEEE Transaction on Multimedia, 2014, 16(5): 1486-1491 [15]Liao Xin, Shu Changwen. Reversible data hiding in encrypted images based on absolute mean difference of multiple neighboring pixels[J], Journal of Visual Communication and Image Representation, 2015, 28(4): 21-27 [16]Li Ming, Xiao Di, Peng Zhongxian, et al. A modified reversible data hiding in encrypted images using random diffusion and accurate prediction[J]. ETRI Journal, 2014, 36(2): 325-328 [17]Zhang Xinpeng. Separable reversible data hiding in encrypted image[J]. IEEE Trans on information forensics and security, 2012, 7(2): 826-832 [18]Xiao Di, Chen Shoukuo. Separable data hiding in encrypted image based on compressive sensing[J]. Electronics Letters, 2014, 50(8): 598-600 [19]Zhang Minqing, Ke Yan, Su Tingting. Reversible steganography in encrypted domain based on LWE[J]. Journal of Electronics & Information Technology, 2016, 38(2): 354-360 (in Chinese)(张敏情, 柯彦, 苏婷婷. 基于LWE的密文域可逆信息隐藏[J]. 电子与信息学报, 2016, 38(2): 354-360) [20]Lyubashevsky V, Peikert C, Regev O. On ideal lattices and learning with errors over rings[J]. Journal of the ACM, 2013, 60(6): Article 43(1)-43(23) [21]Regev O. On lattices, learning with errors, random linear codes and cryptography[J]. Proceeding of the Annual ACM Symposium of Theory of Computing, 2009, 56(6): 84-93 [22]Yu Weichi. Lattice basis reduction theory and applications in crypto scheme designing[D]. Chengdu: South West Jiao Tong University, 2005 (in Chinese)(余位驰. 格基规约理论及其在密码设计中的应用[D]. 成都: 西南交通大学, 2005) [23]Regev O. The learning with errors problem[C] //Proc of the 25th Annual IEEE Conf on Computational Complexity (CCC 2010). Los Alamitos, CA: IEEE Computer Society, 2010: 191-204 [24]Akinori K, Keisuke T, Keita X. Multi-bit cryptosystems based on lattice problems[G] //LNCS 4450: Proc of Int Conf on Public Key Cryptograghy (PKC2007). Berlin: Springer, 2007: 315-329 [25]Rückert M, Schneider M. Estimating the security of lattice-based cryptosystems[EB/OL]. (2010-10-06) [2016-08-10]. http://eprint.icur.org/2010/137.pdf [26]Zeng Xiao, Chen Zhenyong, Chen Ming, et al. Invertible image watermarking based on zero coefficient index[J]. Journal of Computer Research and Development, 2010, 47(7): 1304-1312 (in Chinese)(曾骁, 陈真勇, 陈明, 等. 基于零系数索引的可逆图像水印[J]. 计算机研究与发展, 2010, 47(7): 1304-1312) [27]Peng Zaiping, Wang Chunhua, Lin Yuan. A novel four-dimensional multi-wing hyper-chaotic attractor and its application in image encryption[J]. Acta Physica Sinica, 2014, 63(24): 240506-1-240506-10 (in Chinese)(彭再平, 王春华, 林愿. 一种新型的四维多翼超混沌吸引子及其在图像加密中的研究[J]. 物理学报, 2014, 63(24): 240506-1-240506-10) [28]Wang Ran, Xu Mankun, Ping Xijian, et al. Steganalysis of spatial images based on segmentation[J]. Acta Automatica Sinica, 2014, 40(12): 2936-2943 (in Chinese)(汪然, 许漫坤, 平西建, 等. 基于分割的空域图像隐写分析[J]. 自动化学报, 2014, 40(12): 2936-2943) [29]Zhang Xinpeng, Qian Zhenxing, Feng Guorui, et al. Efficient reversible data hiding in encrypted image[J]. Journal of Visual Communication and Image Representation. 2014, 25(2): 322-328 [30]Xagawa K, Tanaka K. Proxy re-encryption based on learning with errors (mathematical foundation of algorithms and computer science)[J]. Rims Kokyuroku, 2010, 1691: 29-35 [31]Gentry C. Fully homomorphic encryption using ideal lattices[C] //Proc of the 41st ACM Symp on Theory of Computing (STOC2009). New York: ACM, 2009: 169-178 Ke Yan, born in 1991. MEn candidate. His main research interests include information security, reversible data hiding and cryptography, etc. Zhang Minqing, born in 1967, PhD, professor, PhD supervisor. Her main research interests include cryptography and information security (api_zmq@126.com). Su Tingting, born in 1989. MEn. Her main research interests include information security and network security (suting0518@163.com). A Novel Multiple Bits Reversible Data Hiding in Encrypted Domain Based on R-LWE Ke Yan, Zhang Minqing, and Su Tingting (KeyLaboratoryofNetworkandInformationSecurityUndertheChinesePeopleArmedPoliceForce(EngineeringUniversityofPAP),Xi’an710086) (DepartmentofElectronicTechnology,EngineeringUniversityofPAP,Xi’an710086) Reversible data hiding in encrypted domain is one kind of information hiding techniques which can both extract secret messages and decrypt the embedded ciphertext to restore the original cover vehicle losslessly, possessing privacy protection and data hiding dual function. It is a potential technique in signal processing and data management of the encrypted domain fields. This paper proposes a novel scheme of multiple bits reversible data hiding in encrypted domain based on R-LWE (ring-learning with errors). Multi-band data can be embedded by quantifying the encrypted domain and recoding in the redundancy of cipher text without degrading the hardness of R-LWE algorithm; the embedding recoding method is based on the data distribution during encryption, which maintains the robustness of R-LWE algorithm; By dividing the integer domain into the sub-regions and introducing different quantifying rules, the processes of extraction and decryption can be separated. By deducing the error probability of the scheme, parameters in the scheme which is directly related to the correctness of the scheme is mainly discussed, and reasonable ranges of the parameters are obtained by experiments. When analyzing the security, the probability distribution function of the embedded cipher text is deduced and the statistic features of cipher data are analyzed, which both prove the embedded data isn’t detective. Experimental results have demonstrated that the proposed scheme can not only keep fully reversibility of vehicle recovering and lossless extraction of secret message, but realize that one bit original data can load multiple-bit additional data in encrypted domain, achieving an embedding capacity of 0.2353 bit per every bit of the encrypted data. information security; reversible data hiding; encrypted domain; multiple bits embedding; ring-learning with errors (R-LWE) 2016-06-16; 2016-08-11 国家自然科学基金项目(61379152,61403417) TP309.7 This work was supported by the National Natural Science Foundation of China (61379152,61403417).
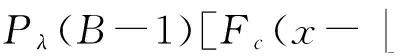
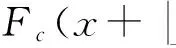
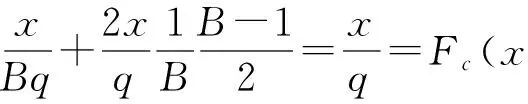
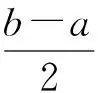

4 结束语



