一个LWE上的短公钥多位全同态加密方案

陈智罡 宋新霞 赵秀凤

1(浙江万里学院电子与计算机学院 浙江宁波 315100)2(浙江万里学院基础学院 浙江宁波 315100)3(信息工程大学三院 郑州 450001) (zhig.chen@foxmail.com)



一个LWE上的短公钥多位全同态加密方案

陈智罡1宋新霞2赵秀凤3

1(浙江万里学院电子与计算机学院 浙江宁波 315100)2(浙江万里学院基础学院 浙江宁波 315100)3(信息工程大学三院 郑州 450001) (zhig.chen@foxmail.com)

目前全同态加密的效率亟待提高，为了提高全同态加密的效率，提出一个LWE(learning with errors)上的短公钥多位全同态加密方案.方案中从离散高斯分布上选取LWE样例，并且将高斯噪音与之相加，导致LWE样例从 2nlogq下降到n+1，使得方案的公钥长度变短.详细给出了该方案的噪音增长分析与安全性证明；此外，对目前密钥交换技术进行了优化，并且针对多位全同态加密，给出了密钥交换优化版本的形式化描述；最后，针对目前全同态加密的实践应用，给出了分析全同态加密具体安全参数的方法.分析了该方案与BGH13方案的具体安全参数，数据显示该方案的具体参数长度要优于BGH13方案.

全同态加密；学习错误问题；多位明文；具体安全参数；格密码

全同态加密能够在不知道密钥的情况下对密文进行任意计算，这种特殊的性质使得全同态加密有广泛的应用需求，例如在云计算数据隐私安全、多方计算、密文检索等.第1个全同态加密方案是由Gentry在2009年提出的[1]，此后人们提出了一些基于不同困难问题的全同态加密方案[2-7]以及对全同态加密效率改进的一些方法[8-11].

目前全同态加密的效率是阻碍其发展的主要问题，而低效率的主要原因之一是其密文尺寸过大.例如LWE(learning with errors)上的加密方案，出于安全性考虑，其密文中包含“噪音”，每次同态计算将引起密文噪音的增长，尤其是密文乘法计算使得密文噪音增长非常快.当噪音超过正确解密所允许的界后，将无法执行同态操作.因此，为了能够执行更多的密文同态操作，必须设置大的参数使得密文有足够的空间容纳噪音，这直接导致了密文尺寸的剧增.

LWE上的加密都是按位加密，即一次加密一位.为了提高全同态加密的计算效率，人们提出了“密文打包(packed ciphertext)”的方法[12]，即将多个明文装入到一个密文中.该方法使得对密文执行一次同态操作，相当于并行对多个明文执行同样的操作.对于环LWE上的全同态加密，由于其环上的特殊性质，可以使用中国剩余定理实现“密文打包”的方法[12]，并且获得了性能上的极大提升[8].此外，Brakerski等人提出了LWE上全同态加密实现“密文打包”的方法[9]，该方案称之为BGH13.

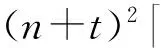
1 预备知识

1.1 基本概念

1.2 LWE问题

LWE问题最早由Regev引入[14]，随后产生了其变种问题环LWE问题[15].LWE问题有3个参数：维数n≥1、整数模q≥2以及一个或q上的概率分布χ.对于一个向量s∈，LWE分布As,χ如下方式获得：随机均匀地选择一个向量a∈以及一个噪音项e←χ，输出(a,b=〈a, s〉+emodq) ∈×q.LWE搜索问题是：给任意数量的独立样例(ai,bi) ←As,χ去发现s.在密码学应用中，更感兴趣的是LWE判定问题：从LWE分布As,χ与均匀分布中分别取出任意相同数量的独立样例，以不可忽略的优势区分LWE分布As,χ与均匀分布.

格上标准困难问题可以归约到LWE问题，目前有2种类型的归约：量子归约[14]与经典归约[16-17].此外，如果向量a取自于分布χ，LWE问题仍然是困难的[18].

1.3 层次型同态加密

一个同态加密方案HE=(Keygen,Enc,Dec,Eval)包含4个多项式时间算法.关于全同态加密的定义，可以参考文献[1,5,19].

有2种类型的全同态加密方案：1)层次型全同态加密方案.该方案的参数依赖于乘法电路深度，方案能够同态执行任意多项式深度的电路.2)“纯”的全同态加密方案.该方案能够执行任意深度的电路.任何一个层次型全同态加密方案 ，都可以通过同态解密技术以及循环安全假设，转换成“纯”的全同态加密方案.

定义1.L-同态.如果一个同态加密方案HE满足如下条件，则称之为L-同态.对于L=L(λ), 如果对于任意深度为L的算术电路f(建立在GF(2)之上)以及任意输入m1,m2,…,ml有：

Pr[HE.Decsk(HE.Evalevk(f,c1,c2,…,cl))≠

f(m1,m2,…,ml)]=negl(λ),

其中,(pk,evk,sk)←HE.Keygen(1λ) 以及ci←HE.Encpk(mi).

定义2. 紧凑性、全同态、层次型全同态加密.如果一个同态加密方案的解密电路独立于所计算的函数，则称之为是紧凑的. 对于任意多项式L，如果一个紧凑的同态加密方案是L-同态，则称之为全同态加密.对于一个全同态加密方案，如果在密钥生成算法中还需要输入1L，则该方案是层次型全同态加密.

2 基本加密方案

当前所有的全同态加密方案都是建立在基本加密方案之上的.本文方案是建立在Lindner和Peikert提出的加密方案之上[13]，但是我们将其改造为多位明文的加密方案，使其一次加密更多的信息.下面我们描述该方案，更重要的是分析其加密噪音和解密噪音.

该方案基于LWE问题，整数q≥2，维数n1和n2，高斯分布D表示为χ，以及随机均匀矩阵了进一步约减公钥尺寸，可以使用系统中共用的信任源生成A.如果系统中没有信任源，可以在密钥生成阶段生成A，即作为公钥的一部分.

1) SecretKeygen(1n2).随机选择一个矩阵S←χt×n2，输出密钥sk=S′←(I|-S)，其中I是t×t单位矩阵.因此密钥sk是一个t×(t+n2)的矩阵，其中每一行可以看成是一个密钥，用于解密多位消息中的一位.

2) PublicKeygen(A,sk).随机选择E←χn1×t,计算B=AST+E∈,输出公钥pk=B.

3) Enc(A,pk,m).为了加密多位消息m∈，随机选取e1←χn1,e2←χt以及e3←χn2,输出:

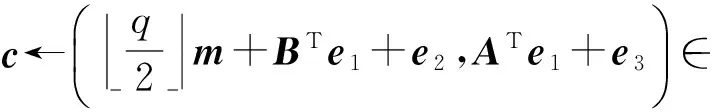
4) Dec(sk,c).计算v←S′c modq，输出:

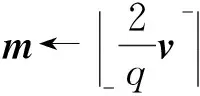
出于安全考虑，加密时引入了噪音，而正确解密依赖于噪音值.下面我们分析加密和解密的噪音值.

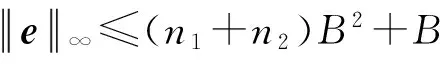
成立.

证明. 由解密定义可知:

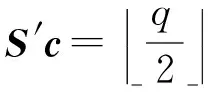
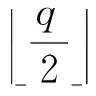
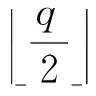
证毕.

我们称e是密文c中的噪音,以上引理给出了“新鲜”密文中的噪音值的上界.

引理2. 解密噪音.随机选择一个矩阵S←χt×n2，令c∈是一个向量,使得：

该解密形式与Regev加密方案[14]的解密形式相同，我们略去其证明.注意，为了恢复消息，|e|应该小于12，因此正确解密的条件是2. 由于2，我们这里取噪音的上界为.下面我们研究该方案的同态性.

3 同态操作

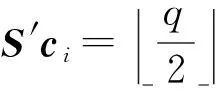
文c1和c2的加法或乘法计算结果c满足:

或

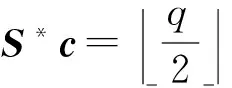
其中,e的值是小的，m1⊙m2表示向量按相应的位乘积，则称密文c在密钥S+下获得了加法同态性，或者密文c在密钥S*下获得了乘法同态性.

3.1 加法同态性

第3节中的基本加密方案本身具有加法同态性.根据定义有:

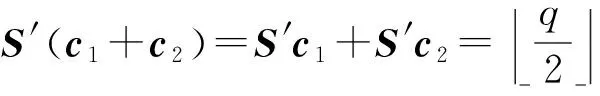
e1+e2(modq).

3.2 乘法同态性

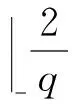
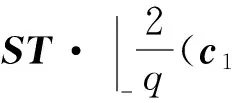
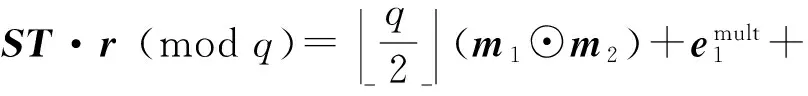
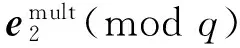
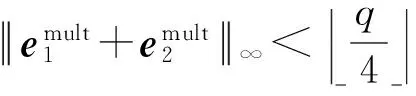
3.3 密钥交换

尽管通过上述乘法定义获得了乘法同态属性，但是它导致了密文与密钥的维数扩张，因此需要使用密钥交换技术[3-4]，将一个高维密文(对应于高维密钥)转换为一个正常维数的密文(对应于正常维数的密钥).但是LWE上密钥交换的效率是不高的.为了约减密钥交换过程中的噪音增长，需要将密文表示为二进制的形式，这导致了密钥交换矩阵的维数扩张.这里我们将引入一个提高密钥交换效率的技巧，并且针对多位全同态加密，对优化的密钥交换过程进行了形式化.

此外，如果仅仅是将密钥ST中的每一行对应的密钥交换矩阵放在一起，形成一个新的密钥交换矩阵的话，这将导致密钥交换的结果是一堆正常维数的密文，而不是一个密文.因此，这里我们需要解决这个问题，必须整体生成一个密钥交换矩阵，使得密钥交换的结果是一个正常维数的密文.

密钥交换包含2个算法:SwitchKeyGen算法用于生成密钥交换矩阵；SwitchKey算法用于将对应于密钥S1的密文转换为对应于密钥[I|S2]的密文.注意在SwitchKeyGen算法中，第2个参数输入的是S2，而不是[I|S2].

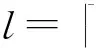
我们称W是密钥交换矩阵.下面我们证明上述密钥交换过程的正确性.

引理3. 令S1,S2,q,A,W是如上在Switch-KeyGen中描述的参数.令c1∈ns，c2←SwitchKey(W,c1)，则有[I|S2]c2=et+S1c1(modq)，其中et=2-lEc1+[I|S2]ew是密文c2中的噪音.

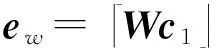
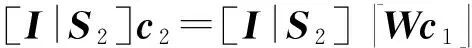
[I|S2]Wc1+[I|S2]ew(modq)=

2-lEc1+[I|S2]ew+S1c1(modq)=

et+S1c1(modq).

由此得证.

证毕.

下面证明密钥交换的安全性.

引理4. 选取S1←χt×ns,生成S2←SecretKeygen(1nt)和W←SwitchKeyGen(S1,S2).假设判定性LWE问题是困难的，则W与(t+nt)×ns上的均匀分布是计算上不可区分的.

证毕.

4 层次型全同态加密方案

深度为L的层次性全同态加密，电路的每一层有一个独立的密钥.同态计算从第L层到第1层，最后一层第0层仅仅是做密钥交换.注意每一次执行同态操作后，需要将密文计算的结果转换为下一层电路的密文(即该密文对应于下一层电路的密钥)，而每一次同态操作前需要2个密文拥有相同的密钥，即“站”在电路的同一层上，否则需要将高层级密文转换为低层级密文.

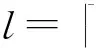
2) FHE.KeyGen(n1,n2,L).对于i=L,L-1,…,1,0，做如下操作:

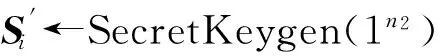
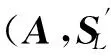
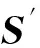
④ 当i=0时,忽略此步.生成Wi→i-1←Switch-KeyGen(STi,Si-1).令pk2={Wi→i-1}.

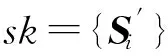
3) FHE.Enc(pk1,m).消息m∈，执行Enc(pk1,m).

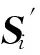
5) FHE.Add(pk2,c1,c2).执行下列步骤：

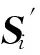
② 否则，如果密文c1,c2有不同的密钥，则调用FHE.RefreshNextLevel算法将高层级密文转换为低层级密文，直到2个密文拥有相同的密钥.然后执行步骤①.

6) FHE.Mult(pk2,c1,c2).执行下列步骤：

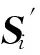
② 否则，如果密文c1,c2有不同的密钥，则调用FHE.RefreshNextLevel算法将高层级密文转换为低层级密文，直到2个密文拥有相同的密钥.然后执行步骤①.

7) FHE.RefreshNextLevel(i,c,Wi→i-1).计算c′=c⊗(1,0,…,0)，输出SwitchKey(Wi→i-1,c′).

下面证明上述方案的安全性.

引理5. 令参数n1,n2,q,χ使得判定性LWE问题是困难的，L是多项式深度.对于任意消息m∈，有(pk1,pk2,sk)←FHE.KeyGen(n1,n2,L),c←FHE.Enc(pk1,m),则(pk1,pk2,c)分布与均匀分布是计算上不可区分的.

证明. 由于pk2={WL→L-1,WL-1→L-2,…,W1→0}和pk1={BL}，考虑分布(BL,WL→L-1,WL-1→L-2,…,W1→0,c)，使用文献[3]中的混合证明方式.首先，根据引理4，W1→0与均匀分布是不可区分的.然后所有Wi→i-1按照降序的方式用均匀分布替换.最后剩下(BL,c)，由于(BL,c)是基本加密方案的公钥和密文，所以(BL,c)是与均匀分布不可区分的.因此，联合分布 (pk1,pk2,c)与均匀分布在计算上是不可区分的.

证毕.

5 噪音分析

同态加法和乘法增长了密文的噪音，尤其是同态乘法极大地增长了噪音.同态加法的噪音就是2个密文的噪音之和，下面重点分析同态乘法的噪音增长.

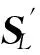
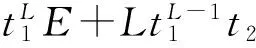
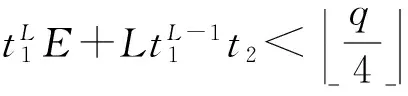
(2)

则结果密文可以正确解密，即可以同态执行深度为L的电路，因此获得了一个层次型全同态加密方案.

6 具体安全参数

由于全同态加密方案的具体安全参数能够反映方案的性能以及在实践应用中非常重要[24-25]，下面我们分析方案的具体安全参数，并且将我们的方案与BGH13方案的参数进行分析比较.选取BGH13方案作为比较的对象，是因为该方案与我们的方案是属于同一类型的全同态加密，具有可比性.

6.1 参数属性

表1列出了我们方案和BGH13方案的参数属性，参数长度用位表示.我们方案的LWE样例的个数是n1，而BGH13方案的样例个数是N=2nlogq. 假设电路深度是L，因此有L+1个密钥和L+1个密钥交换矩阵.注意，密钥交换矩阵视为公钥的一部分，称为计算公钥.如果假设循环安全，计算公钥的个数将是1而不是L+1.本文并不做循环安全假设.显然在我们方案中，公钥长度要小于BGH13方案公钥的logq倍.

Table 1 Some Properties of Two Schemes

6.2 具体参数

目前分析LWE上加密方案的具体安全参数的方法，采用的是区分攻击.区分攻击意味着敌手能够以不可忽略的优势区分LWE实例与均匀实例.区分攻击的本质是在格Λ⊥(A)上发现一个非零的短向量.根据文献[18]，使用目前已知的格基约减算法发现一个长度为β的短向量，需要是δ=2(log2β)(4n log q).对于随机的LWE实例，计算一个root-Hermite因子为δ的约减基的时间(单位为秒)至少为：log(time)≥1.8logδ-110[13].因此给定安全等级λ、模q以及高斯参数r，维数n的下界为

n≥log(qr)(λ+110)7.2.

表2列出了安全等级λ=80，高斯参数r=8，对于不同的模q，其相应的维数最小值.

层次性全同态加密方案需要提前给出所需计算的电路深度L，然后根据电路深度L，从式(2)计算出所需的模q，该模q使得执行深度为L的电路计算后，噪音增长不会超过正确解密的界，从而保证同态性的获得.BGH13方案中没有给出具体的噪音增长分析，我们采用第5节噪音增长分析的方法，获得了执行深度为L的电路计算后，噪音增长为

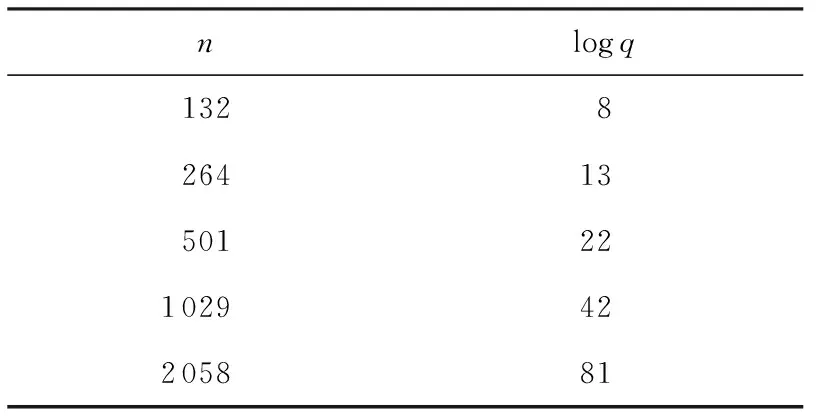
Table 2 Minimal Values of Dimension n

(3)

其中,t3=4(n+t)logq，t4=2(n+t)2Blog3q，“新鲜”密文的噪音是E′=2nBlogq.

表3、表4给出了安全等级是80位，在电路深度L取值0,1,5,10时，模q和维数n的具体取值.注意，公钥长度、密钥长度以及密文长度都是用千比特为单位.数据显示在相同安全等级λ和电路深度L下，我们方案的模q和维数n小于BGH13方案的，其原因是我们方案的噪音增长要小于BGH13方案，从式(2)和式(3)的比较即可知道.由于公钥长度、密钥长度以及密文长度都依赖于模q和维数n的值，而我们方案的公钥和密钥长度的参数属性都比BGH13方案小logq倍，所以直接导致了表3中公钥长度、密钥长度以及密文长度的具体值都要小于BGH13方案.

Table 3 The Sizes of Parameters in Our Scheme

Table 4 The Sizes of Parameters in BGH13

7 结 论

本文提出了一个短公钥的多位全同态加密方案，详细给出了该方案的噪音增长分析与安全性证明.此外，对目前密钥交换技术进行了优化，并且针对多位全同态加密，给出了密钥交换优化版本的形式化描述.最后，针对目前全同态加密的实践应用，给出了分析全同态加密具体安全参数的方法.分析了本文方案与BGH13方案的具体安全参数.数据显示本文方案的具体参数长度要优于BGH13方案.

[1]Gentry C. Fully homomorphic encryption using ideal lattices[C] //Proc of the 41st Annual ACM Symp on Theory of Computing (STOC). New York: ACM, 2009: 169-178

[2]van Dijk M, Gentry C, Halevi S, et al. Fully homomorphic encryption over the integers[G] //LNCS 6110: Advances in Cryptology (Eurocrypt 2010). Berlin: Springer, 2010: 24-43

[3]Brakerski Z, Vaikuntanathan V. Efficient fully homomorphic encryption from (Standard) LWE[C] //Proc of the 52nd IEEE Annual Symp on Foundations of Computer Science. Los Alamitos, CA: IEEE Computer Society, 2011: 97-106

[4]Brakerski Z, Gentry C, Vaikuntanathan V. (Leveled) Fully homomorphic encryption without bootstrapping[C] //Proc of the 3rd Innovations in Theoretical Computer Science Conf. New York: ACM, 2012: 309-325

[5]Brakerski Z. Fully homomorphic encryption without modulus switching from classical gapsvp[G] //LNCS 7417: Advances in Cryptology (Crypto 2012). Berlin: Springer, 2012: 868-886

[6]López-Alt A, Tromer E, Vaikuntanathan V. On-the-fly multiparty computation on the cloud via multikey fully homomorphic encryption[C] //Proc of the 44th Symp on Theory of Computing. New York: ACM, 2012: 1219-1234

[7]Gentry C, Sahai A, Waters B. Homomorphic encryption from learning with errors: Conceptually-simpler, asymptotically-faster, attribute-based[G] //LNCS 8042: Advances in Cryptology (Crypto 2013). Berlin: Springer, 2013: 75-92

[8]Gentry C, Halevi S, Smart N. Fully homomorphic encryption with polylog overhead[G] //LNCS 8042: Advances in Cryptology (Eurocrypt 2012). Berlin: Springer, 2012: 465-482

[9]Brakerski Z, Gentry C, Halevi S. Packed Ciphertexts in LWE-Based Homomorphic Encryption[G] //Public-Key Cryptography (PKC 2013). Berlin: Springer, 2013: 1-13

[10]Alperin-Sheriff J, Peikert C. Faster bootstrapping with polynomial error[G] //LNCS 8616: Advances in Cryptology (CRYPTO 2014). Berlin: Springer, 2014: 297-314

[11]Hiromasa R, Abe M, Okamoto T. Packing messages and optimizing bootstrapping in GSW-FHE faster bootstrapping[G] //LNCS 9020: Public-Key Cryptography (PKC 2015). Berlin: Springer, 2015: 699-715[12]Smart N P, Vercauteren F. Fully homomorphic SIMD operations[J]. Designs, Codes and Cryptography, 2014, 71(1): 57-81

[13]Lindner R, Peikert C. Better key sizes (and attacks) for LWE-based encryption[G] //LNCS 6558: Topics in Cryptology (CT-RSA 2011). Berlin: Springer, 2011: 319-339

[14]Regev O. On lattices, learning with errors, random linear codes, and cryptography[C] //Proc of the 37th Annual ACM Symp on Theory of Computing. New York: ACM, 2005: 84-93

[15]Lyubashevsky V, Peikert C, Regev O. On ideal lattices and learning with errors over rings[G] //LNCS 6110: Advances in Cryptology (Eurocrypt 2010). Berlin: Springer, 2010: 1-23

[16]Peikert C. Public-key cryptosystems from the worst-case shortest vector problem: Extended abstract[C] //Proc of the 41st Annual ACM Symp on Theory of Computing. New York: ACM, 2009: 333-342

[17]Brakerski Z, Langlois A, Peikert C, et al. Classical hardness of learning with errors[C] //Proc of the 45th Annual ACM Symp on Theory of Computing. New York: ACM, 2013: 575-584

[18]Micciancio D, Regev O. Lattice-based cryptography[G] //Post-Quantum Cryptography. Berlin: Springer, 2009: 147-191

[19]Gentry C, Halevi S, Smart N. Homomorphic evaluation of the AES circuit[G] //LNCS 7417: Advances in Cryptology (CRYPTO 2012). Berlin: Springer, 2012: 850-867

[20]Chen Zhigang, Wang Jian, Zhang Zengnian, et al. A fully homomorphic encryption scheme with better key size[J]. China Communications, 2014, 11(9): 82-92

[21]Chen Zhigang, Song Xinxia, Zhang Yanhong. A fully homomorphic encryption scheme based on binary-LWE and analysis of security parameters[J]. Journal of Sichuan University: Engineering Science Edition, 2015, 47(2): 75-81 (in Chinese)(陈智罡, 宋新霞, 张延红. 基于Binary-LWE噪音控制优化的全同态加密方案与安全参数分析[J]. 四川大学学报: 工程科学版, 2015, 47(2): 75-81)

[22]Chen Zhigang, Wang Jian, Chen Liqun, et al. Review of how to construct a fully homomorphic encryption scheme[J]. International Journal of Security and its Applications, 2014, 8(2): 221-230

[23]Chen Zhigang, Wang Jian, Chen Liqun, et al. A regev-type fully homomorphic encryption scheme using modulus switching[J/OL]. Scientific World Journal, 2014 [2016-06-01]. https://www.hindawi.com/journals/tswj/2014/983862/abs/

[24]Yang Xiaoyuan, Zhou Tanping, Zhang Wei, et al. Application of a circular secure variant of LWE in the homomorphic encryption[J]. Journal of Computer Research and Develoment, 2015, 52(6): 1389-1393 (in Chinese)(杨晓元, 周潭平, 张薇, 等. 具有循环安全性的同态加密方案的设计[J]. 计算机研究与发展, 2015, 52(6): 1389-1393)

[25]Liu Mingjie, Wang An. Fully homomorphic encryption and its applications[J]. Journal of Computer Research and Develoment, 2014, 51(12): 2593-2603 (in Chinese)(刘明洁, 王安. 全同态加密研究动态及其应用概述[J]. 计算机研究与发展, 2014, 51(12): 2593-2603)

Chen Zhigang, born in 1972. Associate professor at Zhejiang Wanli University. Received his PhD degree from Nanjing University of Aeronautics and Astronautics. His main research interests include fully homomorphic encryption and lattice-based cryptography.

Song Xinxia, born in 1973. Associate professor at Zhejiang Wanli University. Received her MSc degree in mathematic theory from Zhejiang Normal University. Her main research interests include cryptography and algebra.

Zhao Xiufeng, born in 1977. Associate professor. Received her PhD degree from Shandong University. Her main research interests include cryptography protocols and fully homomorphic encryption.

A Multi-Bit Fully Homomorphic Encryption with Better Key Size from LWE

Chen Zhigang1, Song Xinxia2, and Zhao Xiufeng3

1(CollegeofElectronicandComputer,ZhejiangWanliUniversity,Ningbo,Zhejiang315100)2(CollegeofJunior，ZhejiangWanliUniversity,Ningbo,Zhejiang315100)3(TheThirdSchool,InformationEngineeringUniversity,Zhengzhou450001)

The efficiency of fully homomorphic encryption is a big question at present. To improve the efficiency of fully homomorphic encryption, we use the technique of packed ciphertexts to construct a multi-bit fully homomorphic encryption based on learning with errors (LWE) problem. Our scheme has a short public key. Since our fully homomorphic encryption scheme builds on the basic encryption scheme that chooses learning with errors samples from Gaussian distribution and add Gaussian error to it, which results in that the number of learning with errors samples decrease from 2nlogqton+1. We prove that our fully homomorphic encryption scheme is feasible and its security relies on the hardness of learning with errors problem. In addition, we adapt the optimization for the process of key switching from BGH13 and formal this new process of key switching for multi-bit fully homomorphic encryption. At last, we analyze the concert parameters and compare these parameters between our scheme and BGH13 scheme. The data show that our scheme has smaller public key by a factor of about logqthan the one in BGH13 scheme.

fully homomorphic encryption; learning with errors (LWE); multi-bit plaintext; concert security parameters; lattice-based cryptography

2016-06-16；

2016-08-17

浙江省自然科学基金项目(LY17F020002)；NSFC-浙江两化融合联合基金项目(U1509219)；宁波市自然科学基金项目(2016A610226)

TP309

This work was supported by the Natural Science Foundation of Zhejiang Province of China (LY17F020002), the NSFC-Zhejiang Joint Fund for the Integration of Industrialization Informatization (U1509219), and the Ningbo Natural Science Foundation (2016A610226).