活用课本例题功能，提升数学核心素养

◇　贵州　邹世海(特级教师)

(作者单位：贵州省遵义四中)



活用课本例题功能，提升数学核心素养

◇贵州邹世海(特级教师)

如何贯彻课标理念,摈弃品种繁多的教辅资料,减轻学生负担？本文就实践中充分利用课本资源,挖掘例题功能,通过一题多解、多题一解训练,增强思维发散、收敛、类比、创造等数学核心素养,在高效中完成数学学习活动作如下探索和思考．

下面采取多阶段、多层次、多解法解答本题．

1)初级层次——生生互动,八仙过海各显神通,旨在掌握通法,夯实基础．(可以让中等偏下层次的4位同学上台展示、交流)

方法1作差比较法．因为a、b∈R*,

a3+b3-(a2b+ab2)=(a+b)(a2-ab+b2)-

ab(a+b)=(a+b)(a-b)2>0.

方法2作商比较法．因为a、b∈R*,

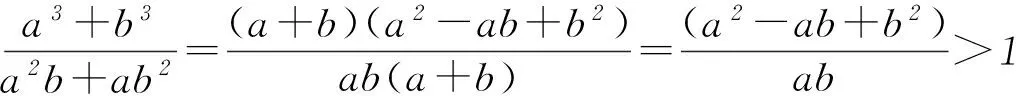
方法3分析法．欲证a3+b3>a2b+ab2,只需a3+b3-(a2b+ab2)>0,只需(a+b)(a2-ab+b2)-ab(a+b)>0,只需(a+b)(a-b)2>0,显然成立．

方法4综合法．因为a、b∈R*,所以

(a+b)(a-b)2>0,

所以(a+b)(a2-ab+b2)-ab(a+b)>0,

a3+b3-(a2b+ab2)>0,a3+b3>a2b+ab2.

2)中级层次——师生互动,通过启发、引导,挖掘潜能,实现超越与飞跃．

方法5基本不等式法.

因为a、b∈R*,由基本不等式,所以

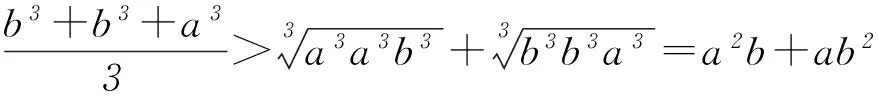
课本练习a、b∈R*,a>b,求证:

a5+b5>a3b2+a2b3.

3)高级层次——数学思想渗透,培养创造性思维,进一步提升核心素养,让优秀思维得到升华．

方法6数形结合构造法.从三维量a3、b3联想正方体体积,从三维量a2b、b2a联想长方体体积,创造性构建几何模型.令AB=a,PK=b,则V正方体AC1=a3,V正方体PF=b3,V长方体AR=a2b,V长方体XF=V长方体JN=ab2.

由整体大于局部可解．

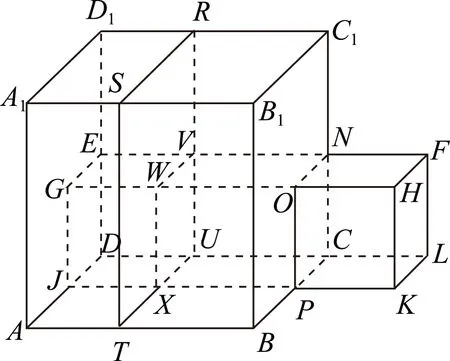
图1

方法7排序不等式法．因为a、b∈R*,a>b,所以a2>b2.由顺序和大于乱序和、大于倒序和可解．

反思:通过层层递进式的一题多解,在开放与民主的课堂里,让学生沉浸于智慧的挑战、快乐地发现与数学美的享受之中,将学生的思维一步步引向深入，体会和感受数学的乐趣,进而得到核心素养的提升．

(作者单位：贵州省遵义四中)