抓住例题本质灵活解中考题

马育伟

抓住例题本质灵活解中考题

马育伟

苏科版九年级《数学》上册第129页有这样一个问题.

【原题】有一个质地均匀的正十二面体，12个面上分别写有1～12这12个整数，投掷这个正12面体.

（1）朝上一面的数有哪些？它们发生的可能性相同吗？

（2）朝上一面的数是奇数与朝上一面的数是偶数，发生的可能性相同吗？

（3）朝上一面的数是4的倍数与朝上一面的数是6的倍数，发生的可能性相同吗？

【思路点拨】投掷这个正12面体时，每个面向上是等可能的事件，因此朝上一面可能为1～12这12个整数中的某个，每个面发生的可能性是相同的.而1～12中有6个奇数和6个偶数，所以朝上一面的数是奇数与朝上一面的数是偶数发生的可能性相同，但在1～12中有3个4的倍数和2个6的倍数，因此它们发生的可能性不相同。

【自主解答】（1）朝上一面的数有1、2、3、4、5、6、7、8、9、10、11、12，它们发生的可能性相同.

（2）朝上一面的数是奇数与偶数发生的可能性相同.

（3）朝上一面的数是4的倍数与6的倍数，发生的可能性不相同.

【点评】课本中的这一问题是“中考课堂”的一个例题，即在中考考题中常常会出现的考题类型.概率统计题作为初中数学的核心内容，要求学生充分理解事件的等可能性及发生某一事件的可能性大小求法——求概率的常用方法是先计算随机事件发生的总可能情况数A及发生某一事件的可能情况数B，而概率的确定就是的值.

变式1（2013·福建厦门）有一个质地均匀的正12面体，12个面上分别写有1～12这12个整数（每个面上只有一个整数且每个面上的整数互不相同）.投掷这个正12面体一次，记事件A为“向上一面的数是2或3的整数倍”，记事件B为“向上一面的数是3的整数倍”，请你判断等式“P（A）=+P（B）”是否成立，并说明理由.

【思路点拨】投掷这个正12面体时，每个面向上是等可能的事件，因此朝上一面可能为1～12这12个整数中的某个，而2的整数倍为2、4、6、8、10、12共6种，3的整数倍为3、6、9、12共4种，根据这一性质易得答案.

【自主解答】不成立.

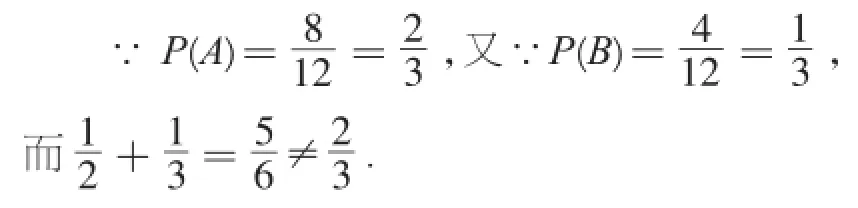
∴等式不成立.

【点评】本题的关键是分别求出事件A与事件B的概率，然后验证等式是否成立.

变式2（2013·江苏无锡）小明与甲、乙两人一起玩“手心手背”的游戏.他们约定：如果三人中仅有一人出“手心”或“手背”，则这个人获胜；如果三人都出“手心”或“手背”，则不分胜负.那么在一个回合中，如果小明出“手心”，则他获胜的概率是多少？（请用“画树状图”或“列表”等方法写出分析过程）

【思路点拨】本题中虽然有三人玩“手心手背”的游戏，但已经确定了小明出“手心”，故只需考虑甲、乙两人出“手心”或“手背”的情况后再去分析小明获胜的概率是多少.

【自主解答】用列表法解题如下：

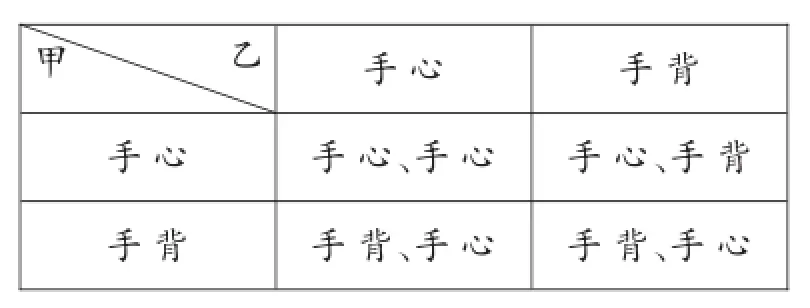
甲乙手心手背手心手心、手心手背、手心手背手心、手背手背、手心

∵小明出“手心”，甲、乙两人出“手心”或“手背”的所有可能有4种情况，而两人都出“手背”只有1种可能，

【点评】本题的关键是能分清题意，是在限定小明出“手心”的条件下的三人游戏，故不要考虑小明出“手背”的情况.

变式3（2016·江苏无锡）甲、乙两队进行打乒乓球团体赛，比赛规则规定：两队之间进行3局比赛，3局比赛必须全部打完，赢满2局的队为获胜队，假如甲、乙两队之间每局比赛输赢的机会相同，且甲队已经赢得了第1局比赛，那么甲队最终获胜的概率是多少？（请用“画树状图”或“列表”等方法写出分析过程）

【思路点拨】本题中虽然甲、乙两队之间进行3局比赛，但已经确定了甲队赢得了第1局比赛，故只需考虑甲、乙两队第2、3局比赛情况后再去分析甲队获胜的概率是多少.

【自主解答】根据题意画出树状图如下：

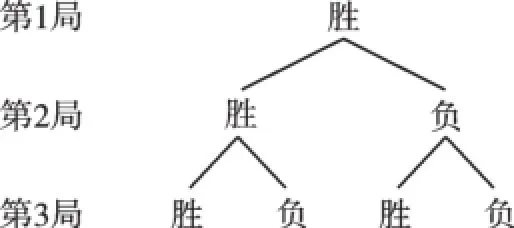
一共有4种情况，确保两局胜的有3种，

【点评】本题的关键是能分清题意，是已知第一局甲胜的情况下求后两局甲获胜情况，故不要考虑第一局甲负的情况.

（作者单位：江苏省无锡市硕放中学）