感受“轴对称”的洪荒之力

张文珠 浦叙德

感受“轴对称”的洪荒之力

张文珠 浦叙德

在图形世界中，有着“点”的灵动、“线”的洒脱、“面”的恢弘，其中，有一类图形变换，看上去成双成对，在图形世界中独放异彩.在此，让我们以“将军饮马”为模型，感受一下“轴对称”带给我们的“洪荒之力”吧！

数学模型

传说亚历山大城有一位精通数学和物理的学者海伦，一位罗马将军专程去拜访他，向他请教一个问题.如图1，将军每天从军营A出发，先到河边l饮马，然后再去河岸同侧的B地开会，应该怎样走才能使路程最短？从此，这个被称为“将军饮马”的问题广泛流传，据说海伦略加思索就解决了它.

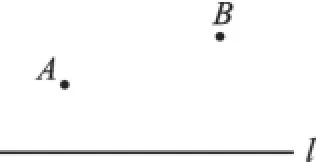
图1

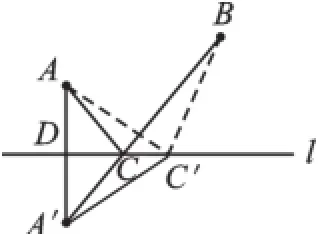
图2

解决方法

如图2，过点A作关于l的对称点A′，连接A′B，与l相交于C，则C点就是饮马的地方，经过C点走，行走路程最短，为AC+CB=A′C+CB= A′B的长度.

如果将军在点C外任一点C′处饮马，所走的路程就是AC′+C′B，连接A′C′，由于AC′+ C′B=A′C′+C′B＞A′B.可见，在C点外任何一点C′处饮马，所走的路程都要远一些.

这里有两点需要说明：（1）由作法可知，河流l相当于线段AA′的中垂线，所以AC=A′C，AC′=A′C′，理论依据为“线段垂直平分线上的点到线段两个端点的距离相等”；（2）A′C′+C′B＞A′B的理论依据为“两点之间线段最短”.

方法总结

1.审题确定关键要素：定点（A、B）、动点（C）、对称轴（l）；2.根据动点（C）所在直线确定对称轴（l）；3.画出定点（A）关于对称轴（l）的对称点（A′）；4.连接所画对称点（A′）和另一个定点（B），所得线段（A′B）的长度即为最短距离.

这是“将军饮马”模型的解决方法，其解题核心是借助“轴对称”的性质将线段“化折为直”.但数学的魅力在于它的变化莫测，题中定点和动点的个数、位置的变化都会影响解题，但“万变不离其宗”，接下来让我们看一看由此模型带来的演变和拓展吧！

例1如图3，在△ABC中，AC=BC，∠ACB= 90°，D是BC边中点，E是AB边上一动点，要使EC+ED值最小，请画出满足该条件的点E的具体位置.

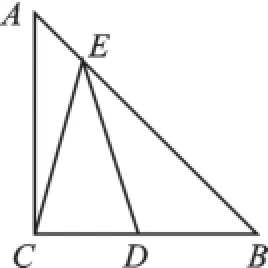
图3

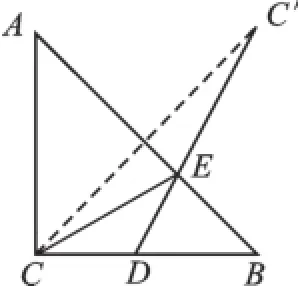
图4

解析：如图4，在线段EC、ED端点中，E为动点，C、D为定点；动点E所在直线AB为对称轴；在定点C、D中任取一点C作关于直线AB的对称点C′；连接所作对称点C′与另外一定点D，线段C′D的长度即为EC+ED的最小值，C′D与对称轴AB的交点即为点E.

说明：动点的作用是确定对称轴，一定点的作用是确定该定点的对称点，另一定点的作用是连接它与所作对称点得一线段，该线段即为“最短距离”；动点的具体位置为连线和对称轴的交点.本题关键首先是利用“轴对称”的性质“化折为直”，其次是依据“两点之间，线段最短”.

例2如图5，在等边△ABC中，AD是BC边上的中线，M是AD上一动点，E是AC边上一动点，如果使ME+MC值最小，请在图中画出动点E和M的具体位置.

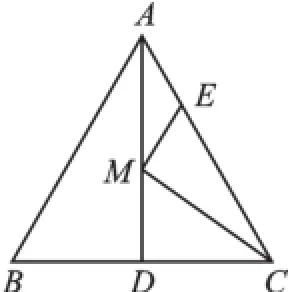
图5

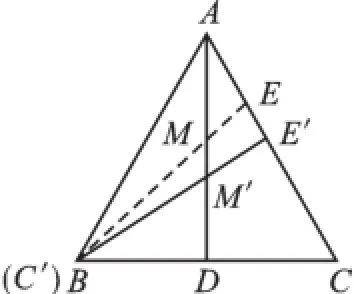
图6

解析：如图6，线段ME、MC端点中的M、E为动点，C为定点；动点M、E所在直线AD或AC为对称轴，但定点C在AC上，所以确定直线AD为对称轴；作定点C关于直线AD的对称点C′

（由等边三角形的轴对称性可知点C′与点B重合）；连接所作对称点C′与另外一动点E，得一线段（如图C′E），因为点E在AC边上滑动，所以当C′E⊥AC时，C′E才是最短的，此时E在E′处，C′E′的长度即为ME+MC的最小值，垂足E′即为动点E的具体位置，C′E′与AD的交点M′即为动点M的具体位置.

说明：例2与例1不同之处在于首先出现2个动点，因此在对称轴的确定上需根据定点C的位置确定（若以直线AC为对称轴，则定点C的对称点为本身，从而无法深入解题）；其次例1连接的是两定点，而本例连接的是一定（C′）一动（E），因此解题关键在于利用“轴对称”的“化折为直”，再利用“点线之间，垂线段最短”.

例3如图7，在四边形ABCD中，∠BAD= 120°，∠B=∠D=90°，在BC、CD上分别找一点M、N，使得△AMN的周长最小，并求此时∠AMN+∠ANM的度数.

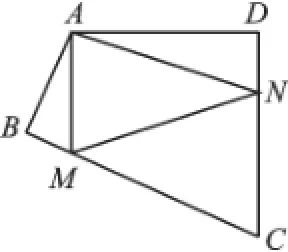
图7

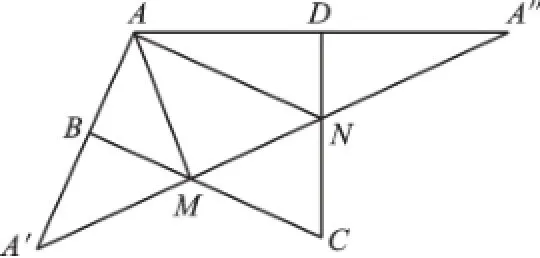
图8

解析：如图8，△AMN三顶点中M、N为动点，A为定点；动点M、N所在直线BC、DC为对称轴；作定点A关于直线BC的对称点A′，作定点A关于直线CD的对称点A″；连接所作对称点A′与A″，线段A′A″的长度即为△AMN周长的最小值，A′A″与BC、DC的交点即为动点M、N的具体位置；利用三角形和轴对称的相关性质求得∠AMN+∠ANM的度数为120°.

说明：例3与例1、例2的不同在于△AMN周长为三边长之和，是求AM+AN+MN的最小值，因此在“化折为直”的宗旨下，作了两次轴对称，将三条线段拼在了一条线段A′A″上，因为点A′、A″均为定点A的对称点，所以本题的理论依据为“点点之间，线段最短”.

以上3例均是围绕“将军饮马”模型而展开的，似变非变，各放异彩.同学们在学习本章内容、解决相关问题时，如果充分利用“轴对称”的“洪荒之力”，必定会在“将军饮马”模型类题目的解决中所向披靡，百战百胜！

（作者单位：江苏省无锡市新吴区第一实验学校、江苏省无锡市新吴区教师发展中心）