基于改进DFT相位差的正弦波频率估计*
王晓峰,邢敏捷,刘 歌,赵汝鹏
(1.空军航空大学 信息对抗系,长春 130022;2.解放军93175部队,长春 130051)
基于改进DFT相位差的正弦波频率估计*
王晓峰**,邢敏捷2,刘歌1,赵汝鹏1
(1.空军航空大学 信息对抗系,长春 130022;2.解放军93175部队,长春 130051)
针对基于离散傅里叶变换(DFT)相位差的正弦波频率估计方法对频偏敏感的问题,提出了一种改进DFT相位差频率估计方法。首先推导了DFT相位差法频率估计的均方误差,然后提出了基于Rife插值的改进DFT相位差频率估计方法,较好地解决了正弦波频率估计对频偏敏感的问题。仿真实验结果表明,改进方法在各种频偏下均能取得较高的估计精度,估计性能接近克拉美罗限(CRLB)。
正弦波频率估计;频偏敏感;DFT相位差;Rife插值
1 引 言
正弦波信号频率估计在雷达、通信、声纳以及电子对抗等诸多涉及信号处理的领域有着广泛的应用,且经常作为其他复杂信号处理的基础工具,具有十分重要的研究价值[1-5]。文献[6]给出了加性高斯白噪声背景下正弦波频率的最大似然估计,估计性能接近克拉美罗限(Cramer-Rao Lower Bound,CRLB),是最优估计,但该方法需要进行一维搜索,计算量太大,无法工程实现[7]。基于离散傅里叶变换(Discrete Fourier Transform,DFT)的快速傅里叶变换(Fast Fourier Transform,FFT)计算速度快,适合于实时处理,特别是随着硬件技术的迅速发展,基于DFT的频率估计方法获得了广泛应用,但DFT算法栅栏效应导致的频偏严重影响了频率估计精度。文献[8]提出利用信号FFT的最大两根谱线进行插值估计正弦波频率,即Rife算法。但Rife算法没有考虑到噪声的影响,在信噪比较低且信号实际频率接近FFT量化频率点时,容易出现插值方向的错判,影响频率估计精度。为此,相继出现了基于Rife算法的各种改进正弦波频率估计方法[9-12],但这些方法均没有有效解决频偏对Rife算法频率估计性能的影响。文献[13]利用DFT相位直接估计信号频率,但存在相位模糊问题。为解决DFT相位估计信号频率时的相位模糊问题,文献[14]提出了基于DFT相位差的频率估计算法,该方法通过计算两段DFT谱线峰值处的相位差完成频率估计,但当信号频率位于两根DFT量化谱线之间时,噪声将严重影响DFT的相位提取,进而导致频率估计错误。
针对上述文献研究的不足,本文提出一种基于Rife插值的改进DFT相位差频率估计方法,介绍了DFT相位差法频率估计原理,推导了DFT相位差法频率估计的均方误差,最后结合Rife插值思想给出了一种改进的DFT相位差频率估计方法。理论分析表明改进方法能够较好地解决频偏对正弦波频率估计的影响。仿真实验结果验证了改进估计方法的有效性。
2 DFT相位差频率估计
2.1算法原理
频率为f0,初始相位为φ0,幅值为a的正弦波信号可以表示为
s(n)=a·exp[j(2πf0Tn/N+φ0)],n=0,1,…,N-1。
(1)
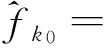
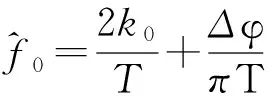
(2)
2.2性能分析
DFT最大谱线处幅值的输出信噪比可近似为[7]
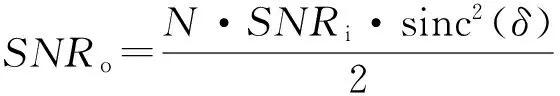
(3)
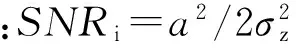
被噪声污染信号r(n)的DFT最大谱线处的相位φk0可以表示为[14]
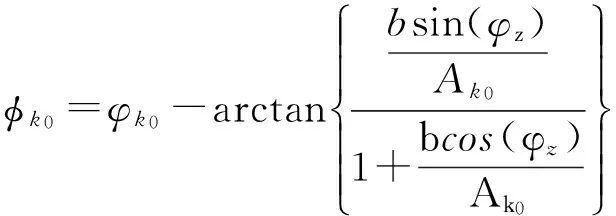
(4)
式中:φk0为信号s(n)的DFT最大谱线处相位;Ak0为DFT最大谱线幅值;φz为噪声DFT相位。式(4)第二项即为噪声产生的相位误差。
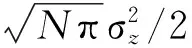
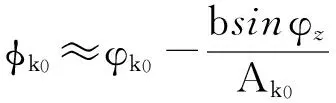
(5)
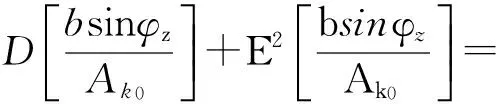
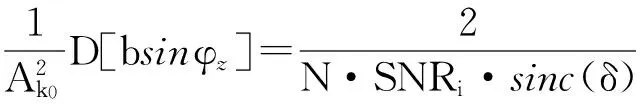
(6)
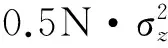
综上所述,DFT相位差频率估计均方误差可近似为
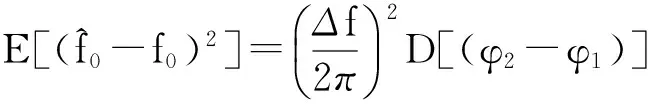
(7)
根据噪声DFT的不相关特性[6],上式可写为
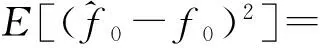
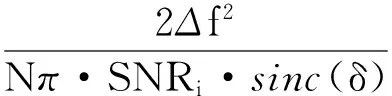
(8)
结合sinc函数特性可知,当信号频率位于DFT某个离散频率附近时,频偏δ的绝对值较小,DFT相位差频率估计具有较高的估计精度,但是当信号频率位于两个离散频率的中心区域时,频偏δ的绝对值较大,DFT相位差法频率估计误差较大,而实际应用中DFT最大谱线对应频率与实际频率的频偏是不可控因素。
3 改进频率估计方法
文献[8]提出利用信号频谱的最大两根谱线进行插值对正弦波频率进行估计:
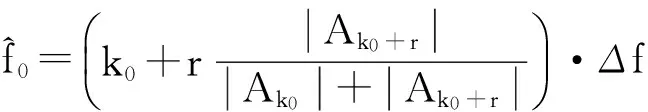
(9)
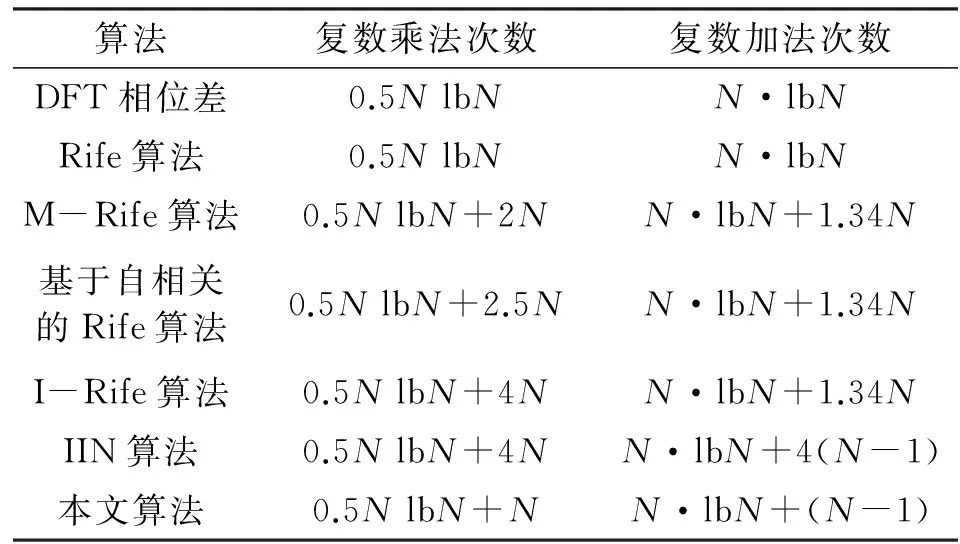
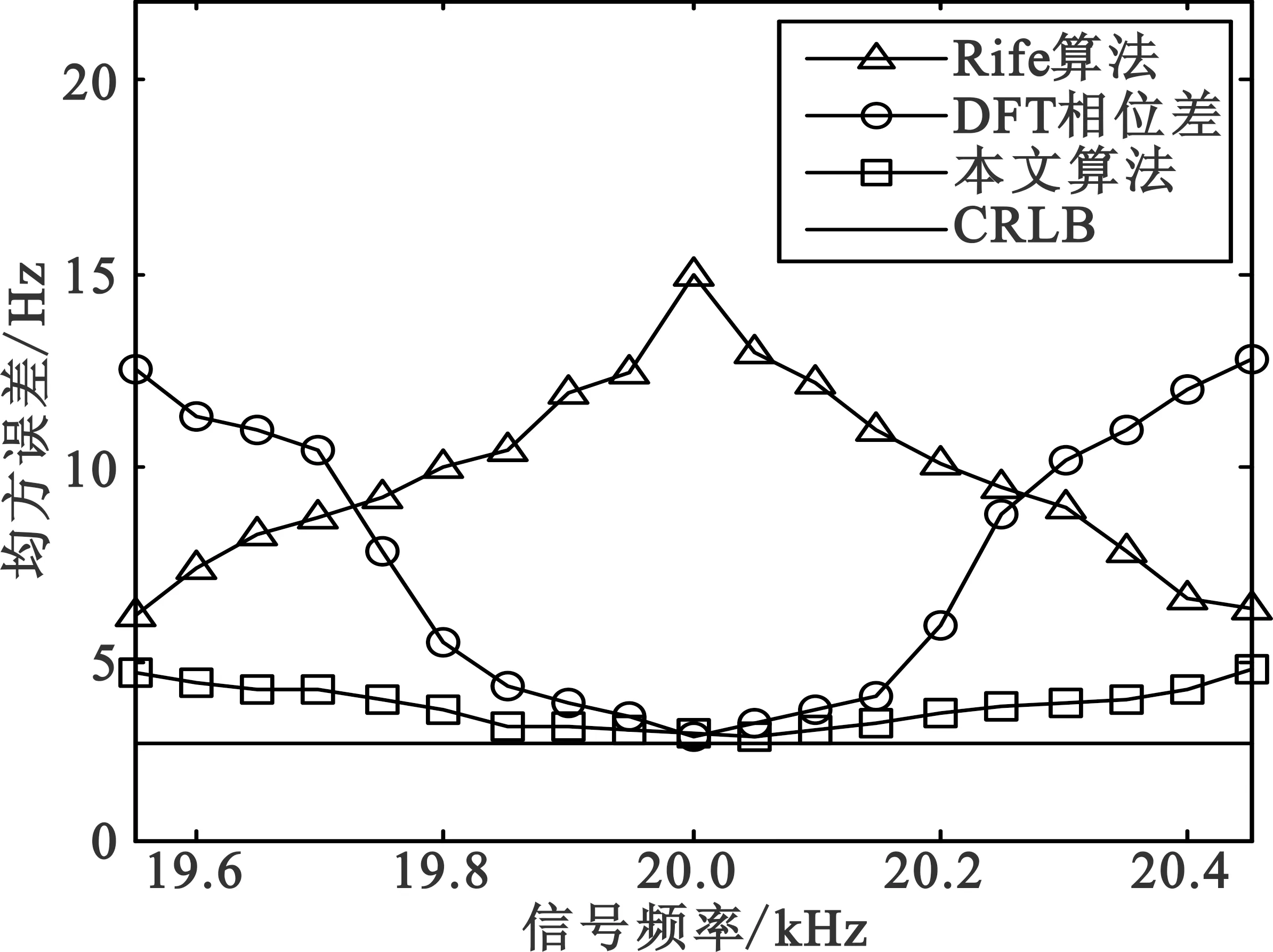
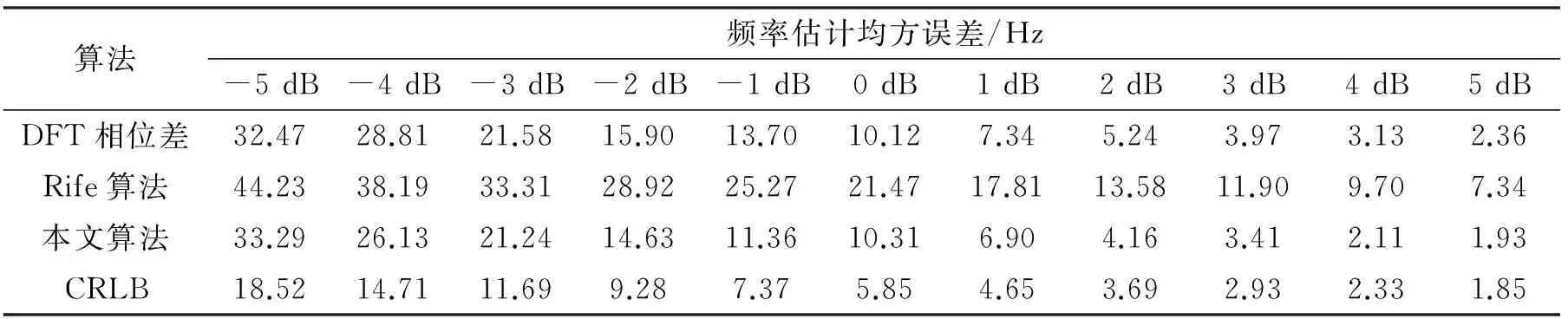
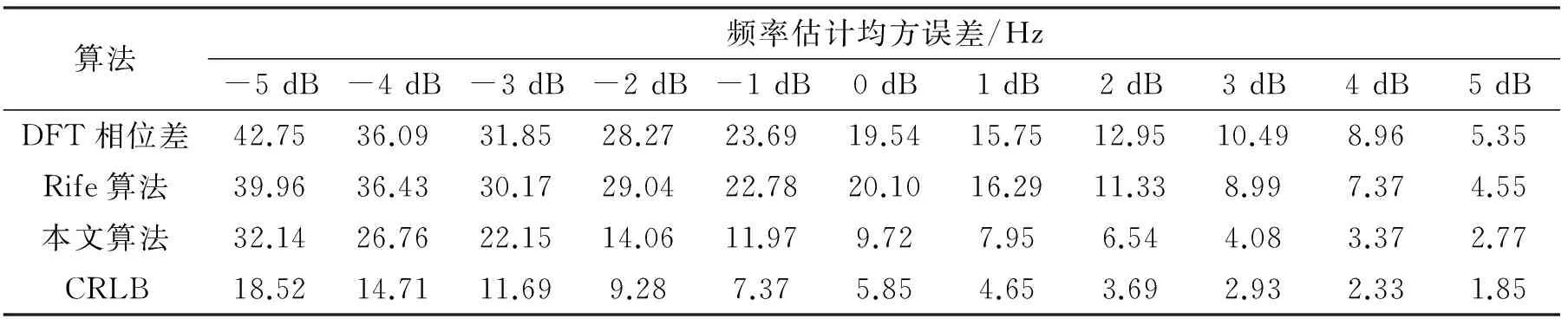
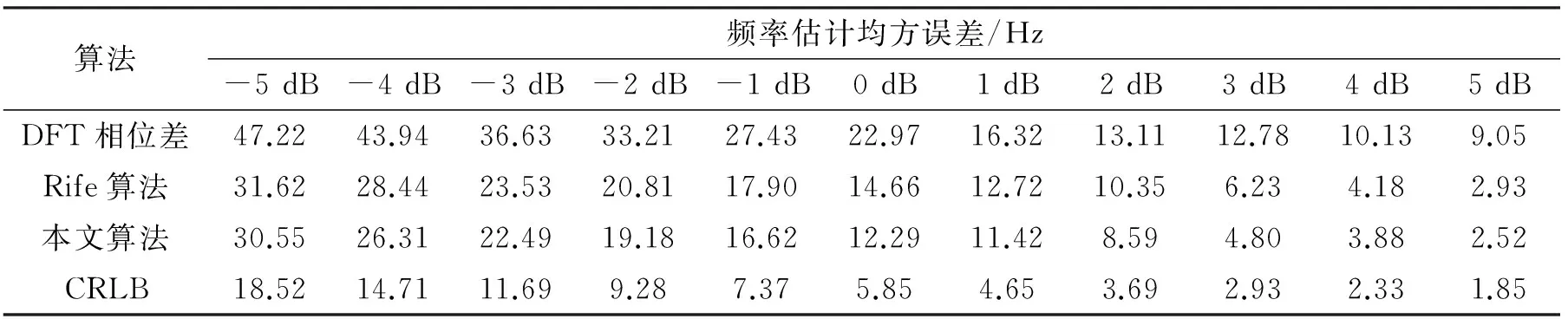
当Ak0+1 (1)将序列分为两个长度相同的序列s1(n)和s2(n),分别计算其N/2点DFT并搜索出最大频谱对应的量化频点k0。 (2)利用Rife插值计算信号频移的量化频率单位δ0: (10) (3)将序列s1(n)和s2(n)频移δ0个量化单位后,利用频谱细化技术分别计算 综上所述,随着新时期的发展,银行理财业务将逐渐多元化发展,满足人民在传统存储的基础上开展灵活的投资,银行必须把握我国经济及国民经济较为深厚的机遇,发挥自身特点,积极与保险、证券等行业跨行业、跨机构开展合作,并在银监会的监管下,合理设计及销售产品,标准化管理,公开、透明的信息披露,为消费者提供可靠的金融投资环境,吸引众多投资资金,推动银行改革升级。 (11) (12) (4)分别提取S1(k0+δ0)和S2(k0+δ0)的相位,计算相位差 Δφ=angle[S2(k0+δ0)]-[S1(k0+δ0)]。 (13) (5)计算信号频率的估计值 (14) 进行Rife插值时,若信号频率位于两个离散频率的中心区域,Ak0和Ak0+r的值较为接近,Rife插值能够很好地将信号频率搬移至k0附近,提高DFT相位差法的估计精度;若信号频率与k0较为接近,Ak0将远远大于Ak0+r,此时计算所得δ0将非常小,即频率搬移后的信号频率仍然位于k0附近。改进DFT相位差频率估计方法对频率与DFT最大谱线位置的相对关系不敏感,较好地解决了频偏对频率估计的影响。 4.1复杂度分析 基于改进DFT相位差的频率估计方法除需要作两次N/2点的FFT外,还需计算两次单点DFT和利用反正切函数计算一次相位。两次N/2点的FFT共需要N/2·lbN次复数乘法和N·lbN次复数加法,两次单点DFT共需要N次复数乘法和N-1次复数加法。在采样点数N较大的情况下,反正切的计算量可以忽略。各基于DFT的正弦波频率估计算法的计算复杂度如表1所示。由表1可知,本文估计算法的计算复杂度略大于DFT相位差法和Rife算法,远小于其他Rife修正算法,能够满足实际应用要求。 表1 各基于DFT的正弦波频率估计算法计算复杂度 4.2仿真分析 为验证基于改进DFT相位差的频率估计性能,将其与DFT相位差法、Rife算法以及频率估计的CRLB进行对比仿真。仿真中信号采样点数N=1 024,采样频率为1 024 kHz,DFT谱线间隔为1 kHz,信噪比为3 dB。正弦信号频率由(19.5,20.5)kHz均匀地选取19个频率值,即频偏δ∈(-0.5,0.5)。每个频率点作500次蒙特卡洛仿真实验,并计算均方误差,仿真实验结果如图1所示。 图1 不同频偏下频率估计性能对比 为进一步验证基于改进DFT相位差的正弦波频率估计方法的性能,在不同信噪比下对其进行仿真验证,并与DFT相位差法、Rife算法以及CRLB进行比较。仿真实验中信号采样点数N=1 024,采样频率为1 024 kHz,DFT谱线间隔为1 kHz,信噪比步进1 dB,每个信噪比下进行500次蒙特卡洛仿真实验。表2~4分别是信号频率为19.9 kHz(δ=0.1)、20.3 kHz(δ=0.3)和20.45 kHz(δ=0.45)时的频率估计均方误差。 表2 δ=0.1时的频率估计性能 表3 δ=0.3时的频率估计性能 表4 δ=0.45时的频率估计性能 实验结果表明,本文算法在各信噪比下的频率估计性能均优于DFT相位差法和Rife算法,对各种频偏具有较好的适应性,较好地解决了频偏对正弦波频率估计的影响,估计性能接近CRLB。 本文研究了正弦波信号的频率估计问题,首先推导了DFT相位差频率估计的均方误差,然后针对DFT相位差频率估计不适用于频偏较大的问题,提出了基于改进DFT相位差的正弦波频率估计方法。改进方法较好地融合了DFT相位差分法和Rife算法的优点,能够适应各种频偏,频率估计性能接近CRLB,且算法计算简单,具有较好的工程应用价值。 [1]YAMADA T. High-accuracy estimations of frequency,amplitude,and phase with a modified DFT for asynchronous sampling[J].IEEE Transactions on Instrumentation and Measurement,2013,62(6):1428-1435. [2]FU H,KAM P Y. Phase-based,time-domain estimation of the frequency and phase of a single sinusoid in AWGN—the role and applications of the additive observation phase noise model[J].IEEE Transactions on Information Theory,2013,59(5):3175-3188. [3]RAMASAMY D,VENKATESWARAN S,MADHOW U.Compressive parameter estimation in AWGN[J].IEEE Transactions on Signal Processing,2014,62(8):2012-2027. [4]高瑞令,吴晓富,颜俊,等. 改进的 DFT 正弦信号频率估计[J].信号处理,2014,30(9):1072-1077.GAO Runling,WU Xiaofu,YAN Jun,et al.Frequency estimator based on autocorrelation with low SNR[J].Journal of Signal Processing,2014,30(9):1072-1077.(in Chinese) [5]侯盼卫,杨录. 基于自相关检测法和能量重心法的正弦信号频率估计算法[J].科学技术与工程,2014(3):97-102.HOU Panwei,YANG Lu. Frequency estimation algorithm of sinusoid signal based on autocorrelation detection and energy centrobaric correction method[J].Science Technology and Engineering,2014(3):97-102.(in Chinese) [6]RIFE D C,BOORSTYN R R. Single tone parameter estimation from discrete time observation[J].IEEE Transactions on Information Theory,1974,20(5):591-598. [7]ABATZOGLOU T J.A fast maximum likelihood algorithm for the frequency estimation of a sinusoid based on Newton's method[J].IEEE Transactions on Acoustics,Speech,and Signal Processing,1985,33(1):77-89. [8]RIFE D C,VINCENT G A. Use of the discrete Fourier transform in the measurement of frequencies and levels of tones[J].Bell System Technical Journal,1970,49(2):97-228. [9]黄超,索继东,于亮. 基于自相关函数相位的正弦信号频率估计新算法[J].电讯技术,2014,54(1):63-67. HUANG Chao,SUO Jidong,YU Liang.A novel algorithm for estimation of sinusoid frequency based on argument of sample autocorrelation function [J].Telecommunication Engineering,2014,54(1):63-67.(in Chinese) [10]周龙健,罗景青,房明星. 基于IIN算法和Rife算法的正弦波频率估计算法[J].数据采集与处理,2013,28(6):839-842. ZHOU Longjian,LUO Jingqing,FANG Mingxing.Frequency estimation of sinusoid wave based on IIN algorithm and Rife algorithm[J].Journal of Data Acquisition and Processing,2013,28(6):839-842.(in Chinese) [11]孙宏军,徐冠群. 基于相角判据的Rife算法的涡街信号处理方法[J].仪器仪表学报,2013,34(12):2860-2866. SUN Honjun,XU Guanqun. Modified Rife frequency estimation algorithm based on phase criterion for vortex signal processing[J].Chinese Journal of Scientific Instrument,2013,34(12):2860-2866.(in Chinese) [12]刘福东,陈智远. 基于Rife算法的频率估计及其FPGA实现[J].工业控制计算机,2014(4):89-90.LIU Fudong,CHEN Zhiyuan. Frequency estimation based on Rife algorithm and its implementation on FPGA[J].Industrial Control Computer,2014(4):89-90.(in Chinese) [13]刘渝. 快速高精度正弦波频率估计综合算法[J].电子学报,1999,27(6):126-128. LIU Yu.A fast and accurate single frequency estimator synthetic approach[J].Acta Electronica Sinica,1999,27(6):126-128.(in Chinese) [14]齐国清,贾欣乐. 基于DFT相位的正弦波频率和初相的高精度估计方法[J].电子学报,2001,29(9):1164-1167. QI Guoqing,JIA Xinle. High accuracy frequency and phase estimation of single tone based on phase of DFT[J].Acta Electronica Sinica,2001,29(9):1164-1167.(in Chinese) 王晓峰(1987—),男,河北承德人,2015年获博士学位,现为讲师,主要研究方向为信号与信息处理; WANG Xiaofeng was born in Chengde,Hebei Province,in 1987. He received the Ph.D.degree in 2015. He is now a lecturer. His research concerns signal and information processing. Email:wxf870516@126.com 邢敏捷(1977—),女,吉林长春人,2009年获硕士学位,现为工程师,主要研究方向为通信与信息系统; XING Minjie was born in Changchun,Jilin Province,in 1977.She received the M.S. degree in 2009. She is now an engineer.Her research concerns communication and information system. 刘歌(1991—),女,山东威海人,2014年获学士学位,现为硕士研究生,主要研究方向为雷信号处理; LIU Ge was born in Weihai,Shandong Province,in 1991. She received the B.S.degree in 2014. She is now a graduate student. Her research concerns radar signal processing. 赵汝鹏(1993—),男,广东湛江人,2015年获学士学位,现为硕士研究生,主要研究方向为雷达信号处理。 ZHAO Rupeng was born in Zhanjiang,Guangdong Province,in 1993. He received the B.S.degree in 2015. He is now a graduate student.His research concerns radar signal processing. Sinusoidal Signal Frequency Estimation Based on Improved DFT Phase Difference WANG Xiaofeng1,XING Minjie2,LIU Ge1,ZHAO Rupeng1 (1.Information Countermeasure Department,Aviation University of Air Force,Changchun 130022,China;2.Unit 93175 of PLA,Changchun 130051,China) The frequency offset sensitivity problem of discrete Fourier transform(DFT) phase difference method in sinusoid wave frequency estimation is studied.An improved DFT phase difference frequency estimation method is presented. Firstly,the mean-squared error(MSE) of DFT phase difference method is deduced.And then,an improved DFT phase difference frequency estimation method based on Rife interpolation is proposed. The improved method has well solved the problem of sensitivity to frequency offset. The computer simulation results indicate that the improved method has higher estimation accuracy in any frequency offset,and its estimation performance is close to Cramer-Rao lower bound(CRLB). sinusoidal signal frequency estimation;frequency offset sensitivity;DFT phase difference;Rife interpolation 10.3969/j.issn.1001-893x.2016.10.012 2016-03-25; 2016-05-25Received date:2016-03-25;Revised date:2016-05-25 TN911.6 A 1001-893X(2016)10-1129-05 引用格式:王晓峰,邢敏捷,刘歌,等.基于改进DFT相位差的正弦波频率估计[J].电讯技术,2016,56(10):1129-1133.[WANG Xiaofeng,XING Minjie,LIU Ge,et al.Sinusoidal signal frequency estimation based on improved DFT phase difference[J].Telecommunication Engineering,2016,56(10):1129-1133.] **通信作者:wxf870516@126.comCorresponding author:wxf870516@126.com1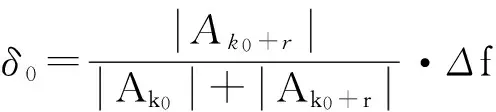
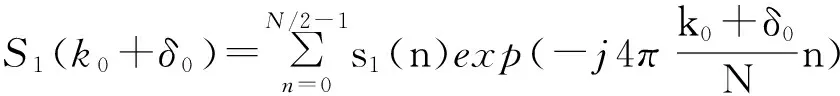
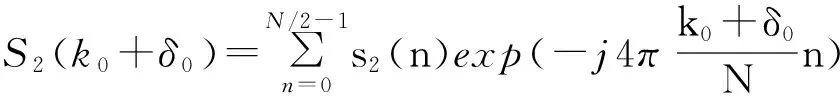
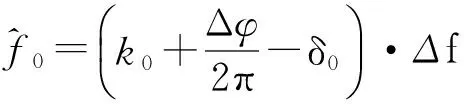
4 性能分析及仿真验证
5 结 论


