抗冲激干扰的稀疏惩罚约束遗漏最小均方算法*
晏国杰,林 云
(重庆邮电大学 移动通信技术重庆市重点实验室,重庆 400065)
抗冲激干扰的稀疏惩罚约束遗漏最小均方算法*
晏国杰**,林云
(重庆邮电大学 移动通信技术重庆市重点实验室,重庆 400065)
当被识别系统是稀疏系统时,传统的遗漏最小均方(LLMS)自适应算法收敛性能较差,特别在非高斯噪声环境中,该算法性能进一步恶化甚至算法不平稳收敛。为了解决因信道的稀疏性使算法收敛变慢的问题,对LLMS算法的代价函数分别利用加权1-norm和加权零吸引两种稀疏惩罚项进行改进;为了优化算法的抗冲激干扰的性能,利用符号函数对已改进的算法迭代式作进一步改进。同时,将提出的两个算法运用于非高斯噪声环境下的稀疏系统识别,仿真结果显示提出的算法性能优于现存的同类稀疏算法。
稀疏系统识别;自适应算法;冲激干扰;收敛性
1 引 言
最小均方(Least-Mean Square,LMS)自适应算法[1]由于具有结构简单和计算复杂度低的特点[2],已经被广泛应用在各工程领域,如控制工程、通信工程、雷达信号处理、干扰消除、有噪声源控制(Active Noise Control,ANC)、生物医学工程、波束成形、语音回声信道等[3-4]。而当输入信号是特征分散较大的时,其传统的LMS自适应算法收敛较慢。为了解决这个问题,Guitlin等利用输入信号特征分散较大这一特点在文献[5]中提出了改进的LMS算法,即遗漏的最小均方(Leaky Least-Mean Square,LLMS)自适应算法。在输入信号的特征分散度较大情况下,LLMS算法的确解决了LMS算法收敛慢的缺陷。
在实际的工程应用中遇到的系统并不总是分散的(稠密的),而有可能是稀疏系统(大部分抽头系数为零或其绝对值小到可以忽略的,只有很少部分活跃抽头的系数较大)。例如:在稀疏的网络回声消除系统中,由于时延效应的影响,在总时隙为64~128 ms的响应中,其活跃的时隙大概只有8~12 ms[6]。当系统是稀疏的时候,LLMS算法收敛性较差。为了解决这个问题,应该研究稀疏的LLMS算法。稀疏的LLMS算法目前研究相对较少,现有的稀疏的LLMS算法主要有Zero-Attracting Leaky Least-Mean-Square(ZA-LLMS)[7]和Weighted Zero-Attracting Leaky-LMS(WZA-LLMS)[8]。在噪声为高斯干扰的情况下,以上两种算法虽然增加了计算抽头系数矢量的一范数的计算复杂度,但是在一定程度上解决了当系统是稀疏的时候LLMS算法收敛慢的问题。在实际的工程应用中,非高斯冲激干扰(包括冲激干扰、冲激干扰和高斯干扰的混合)也是经常遇到的。在非高斯干扰的环境中,以上存在的稀疏类的LLMS算法的性能严重恶化,甚至使算法不能收敛。
本文为了解决稀疏抗非高斯冲激干扰的问题,提出了两个改进的稀疏LLMS算法,即加权零吸引的符号遗漏最小均方算法(Reweighted Zero-Attracting Sign Least Mean Square,RZASLLMS)和基于加权一范数的符号遗漏最小均方算法(Reweighted1-norm Sign Least Mean Square,RL1-SLLMS)。首先,为了利用系统稀疏性这一先验知识,在传统的LLMS算法的代价函数的右边分别加上稀疏约束惩罚函数项(即加权的零吸引项和加权的抽头系数矢量的一范数项),从而使传统的LLMS算法在识别稀疏系统时的收敛速度得到提高。其次,由于符号函数能防止误差因冲激干扰突然剧增而具有抗冲激噪声的性能,被广泛应用于各种自适应算法中[9-10]。受符号函数这一特性的启发,对上一步改进得到的两个迭代方程做进一步修正:分别将两个迭代方程中的误差项用自变量为误差的符号函数代替,以此降低因误差突增而带来算法性能恶化的程度。经过以上两步改进之后就可以分别得到提出的两个算法的迭代方程了,并对提出的算法给出相应的计算复杂度分析。同时,将提出的两个算法运用于稀疏系统识别的Matlab仿真并且与现有的遗漏类算法对比。由于WZA-LLMS的算法性能优于ZA-LLMS的性能,实验只将对WZA-LLMS算法、传统的LLMS算法与提出的算法进行对比。
2 传统的遗漏最小均方自适应算法
2.1系统模型
首先定义一个线性系统识别模型:
d(n)=xT(n)wo+v(n)。
(1)
式中:d(n)表示期望信号;列矢量x(n)=[x(n),x(n-1),…,x(n-L+1)]T为输入信号;wo为待估计系统的抽头系数列矢量;v(n)是背景加性噪声;L是滤波器长度。滤波器的输出可以表示为y(n)=xT(n)w(n),估计误差可表示为
e(n)=d(n)-xT(n)w(n) 。
(2)
式中:w(n)=[w0,w2,…,wL-1]T是wo在第n次迭代的估计列矢量。
2.2遗漏最小均方(LLMS)自适应算法
传统的LLMS算法的代价函数定义如下[11-13]:
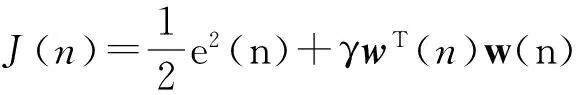
(3)
式中:γ>0为遗漏因子。
由负梯度方向可推导其迭代式如下:
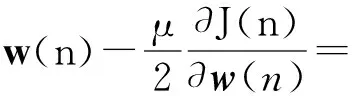
(1-μγ)w(n)+μe(n)x(n)。
(4)
式中:2>μ>0为算法迭代步长。
3 符号最小均方自适应算法SLMS
SLMS算法作为一种抗冲激干扰的算法,其表达式为[14]
w(n+1)=w(n)+μsgn(e(n))x(n)。
(5)
式中:sgn(·)表示符号函数。
3.1提出的RZASLLMS算法
源于Reweighted Zero-Attracting LMS(RZA-LMS)[15]算法的思想,为了使传统的LLMS算法具有稀疏识别性,在传统遗漏的最小均方算法的代价函数的基础上增加稀疏约束惩罚函数项,即
JRZA(n)=J(n)+λRZAJRZA1(n)=
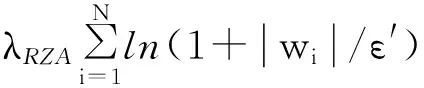
(6)
式中:λRZA>0是一个为了调节估计误差与稀疏控制项的权衡因子。再由负梯度方向可得
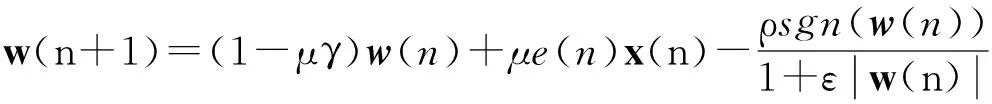
(7)
为了减小因冲激噪声而使误差发生突变给算法收敛性带来的不利影响,利用符号函数对式(7)进一步改进可得RZASLLMS算法的表达式:
w(n+1)=(1-μγ)w(n)+
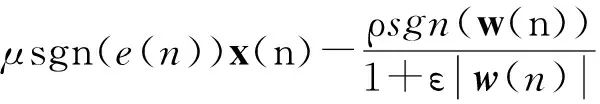
(8)
式中:ρ=μλRZA/ε′,ε=1/ε′,一般ε=20[14]。
3.2提出的RL1-SLLMS算法
由文献[14]知加权的一范数在估计稀疏信道方面有较好的性能,因此,为了增加LLMS算法的稀疏识别性,可以用加权的一范数改进LLMS算法的代价函数为
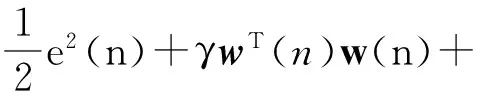
λRL1‖f(n)w(n)‖1。
(9)
式中:λRL1>0与λRZA一样是权衡因子;符号‖·‖1表示向量的一范数;而f(n)被定义[14]为
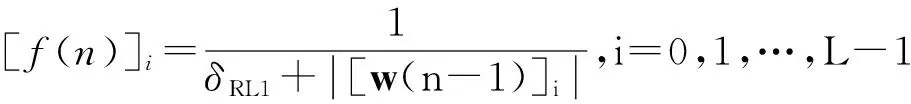
(10)
式中:1>δRL1>0,例如δRL1=0.05,因此,[f(n)]i>0满足i=0,1,…,L-1。
由式(9)负梯度方向迭代有
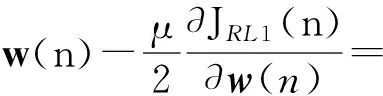
(1-μγ)w(n)+μe(n)x(n)-
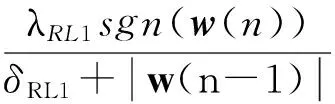
(11)
为了使算法具有抗冲激干扰性,对式(11)进一步改进如下:
w(n+1)=(1-μγ)w(n)+μsgn(e(n))x(n)-
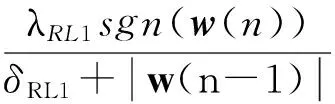
(12)
式中:δRL1>0防止算法初始迭代时除零。
4 提出算法的计算复杂度分析
表1是对LLMS、WZALLMS、RZASLLMS和RL1-SLLMS算法在一次迭代中计算复杂度的对比分析,其中L表示滤波器长度。在统计运算次数时,将加法和减法的计算次数归纳在一起,乘法和除法的计算次数归纳在一起,符号函数的计算次数单独归纳为一项。从表中可以看出传统的LLMS算法计算复杂度是最小的,WZALLMS、RZASLLMS和RL1-SLLMS算法由于都增加了稀疏约束惩罚项,所以都在LLMS算法的基础上增加了2L次加法运算和2L次乘法运算。WZALLMS、RZASLLMS和RL1-SLLMS算法的计算复杂度保持基本相同,其原因是这3个算法都是在LLMS算法的代价函数上增加类似的稀疏约束项进行处理的。而对于提出的RZASLLMS和RL1-SLLMS算法之所以比WZALLMS算法多一次符号函数的运算,是因为提出的算法为了抗冲激干扰对测量误差使用了符号函数。
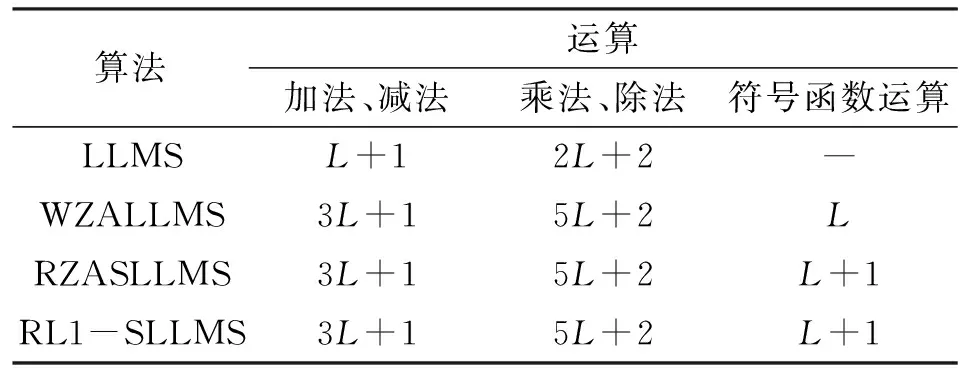
表1 LLMS、WZALLMS、RZASLLMS和RL1-SLLMS算法在一次迭代中的计算复杂度的分析
总之,提出的RZASLLMS和RL1-SLLMS算法虽然与传统的LLMS算法相比计算复杂度相对有些增加,但是与WZALLMS算法相比每一次迭代只增加了一次符号函数的计算。
5 仿真结果
下面对提出的算法做仿真实验分析。由于大部分真实环境的噪声是高斯干扰,而对于另一些情况,如电子设备中的人为噪声、自然现象中的照明高峰等可以描述为非高斯干扰模型[16]。所以实验分为两个部分:第一部分主要验证提出的算法在一般的高斯干扰环境下的稀疏自适应系统识别有良好的均方偏差性能,在被识别系统稀疏程度不同情况下,与现有算法对比;第二部分主要是将噪声换成冲激噪声,与现有算法的对比,同时进一步在语音信道中进行验证。在整个仿真实验过程中,性能学习追踪的归一化均方误差(Normalized Mean Square Deviation,NMSD)表达式为
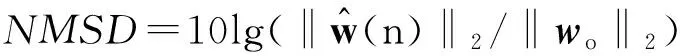
所有的仿真实验的输入信号都是零均值的随机序列通过x(n)=0.9x(n-1)+b(n)产生的,b(n)是零均值、方差为1的高斯噪声。为了避免实验结果的偶然性,所有实验结果都是计算机重复100次独立仿真得到的平均结果。
5.1在高斯干扰下的性能
在输入信号中加入10 dB的零均值的高斯噪声。输入信号通过一个抽头系数为32个的稀疏滤波器,其中2个抽头系数为1,其他的均为0,并定义其稀疏度为2/32。仿真结果如图1所示。所有算法的步长取μ=0.002,遗漏因子取λ=0.000 1[8],λRZA=0.02,ε=20,δRL1=0.05,λRL1=0.000 05[14]。从图1中可以看出,提出的RZASLLMS和RL1-SLLMS算法归一化均方偏差曲线比传统的LLMS算法低,而与WZALLMS算法的归一化学习曲线相差不大。当迭代到5 000次时,系统由wo变到-wo,提出的算法和WZALLMS算法依然保持良好的健壮性。因此,本文提出的两个改进算法优于LLMS算法,和已存在的WZALLMS有相同的稀疏识别性。
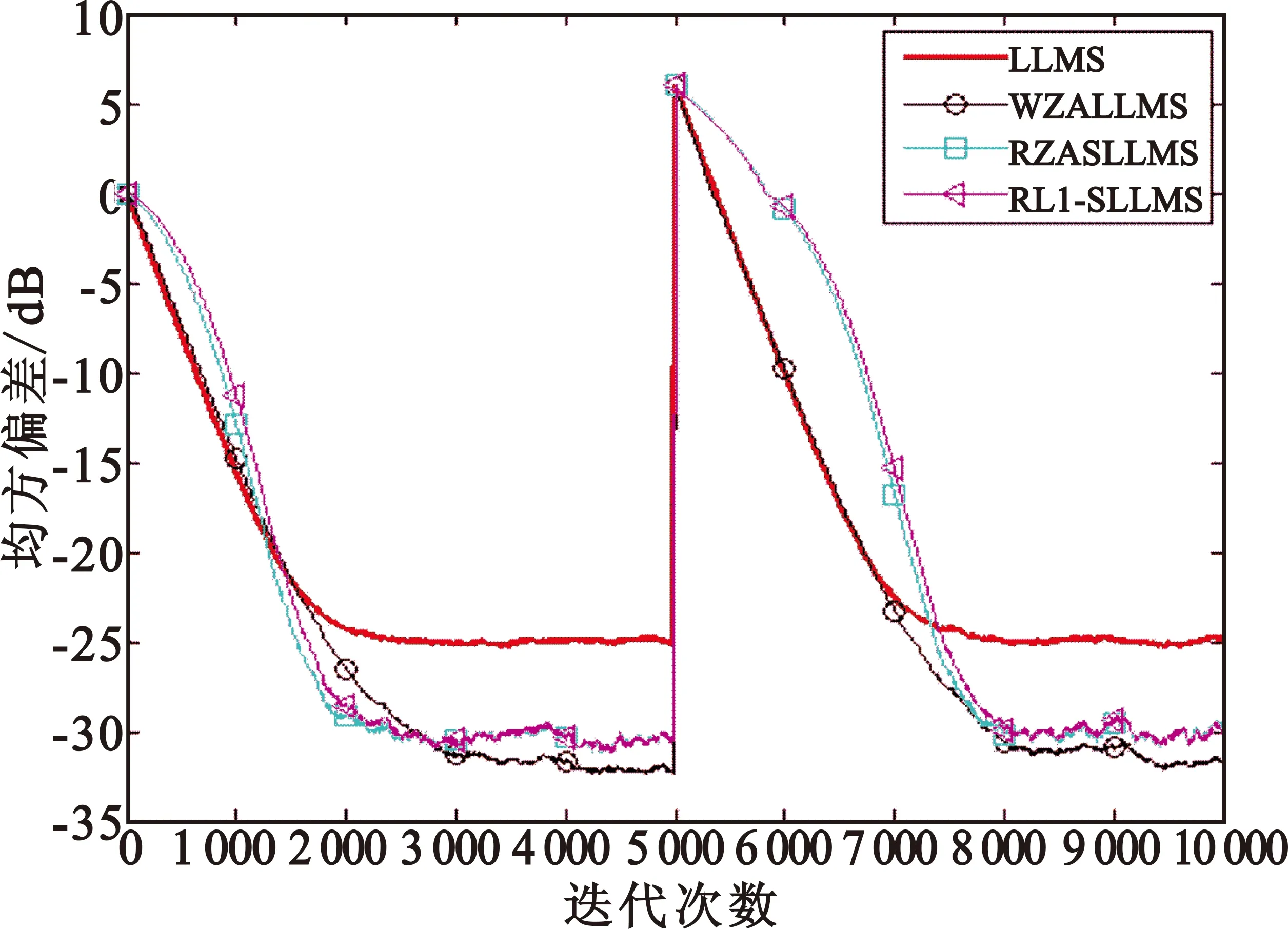
图1 在高斯干扰环境下4种算法的学习曲线比较
为了进一步证实本文提出的算法具有稀疏识别性,在环境噪声与上面实验保持一致的情况下,比较在不同稀疏度(2/32,4/32,6/32,8/32,10/32)算法的性能。如图2,各算的平稳时的NMSD的取值均是在保持相同的收敛速度的前提。从图2中可以看到WZALLMS和提出的RZASLLMS、RL1-LLMS算法的归一化的均方偏差随着稀疏度的增加逐渐向LLMS算法靠拢,这是因为随着稀疏度增加,系统越来越分散,稀疏的自适应算法WZALLMS、 RZASLLMS、RL1-LLMS的收敛性就越来越接近LLMS算法了。除此之外,LLMS算法的曲线基本保持水平,这是因为其步长一直没有改变。由于符号算法自身有收敛慢的特点[9-10],所以正如图1和图2所示,提出的算法的均方偏差稍微高于WZALLMS算法。虽然RZASLLMS和RL1-SLLMS算法与WZALLMS算法相比牺牲了少于1 dB的均方偏差,但是与之前的LLMS算法相比具有良好的收敛性。同时,正如接下来的实验要分析的,提出的算法拥有以上算法不具有的抗冲激性能。
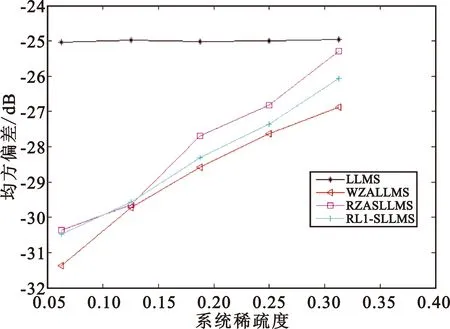
图2 不同稀疏度下的各算法的平稳时的NMSD学习曲线
5.2非高斯干扰下的性能
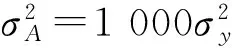
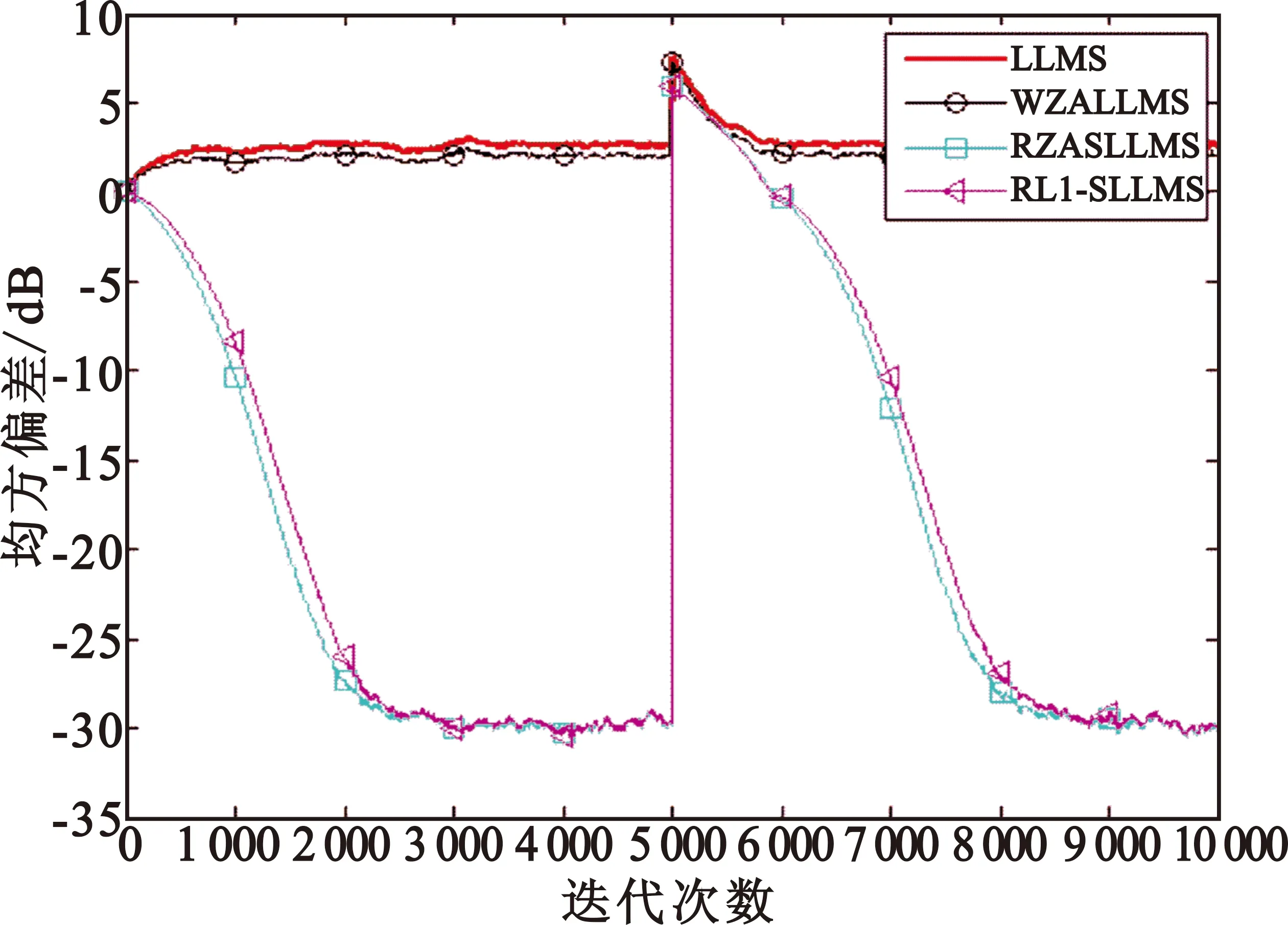
图3 在非高斯干扰下各算法的学习曲线对比
为了进一步验证提出的算法在稀疏系统识别的实用性,下面将实验信道换成如图4所示的随机产生稀疏语音回声信道。利用这个信道做两次仿真,一次仿真的噪声是高斯的,一次为非高斯干扰,其结果分别如图5和图6所示。
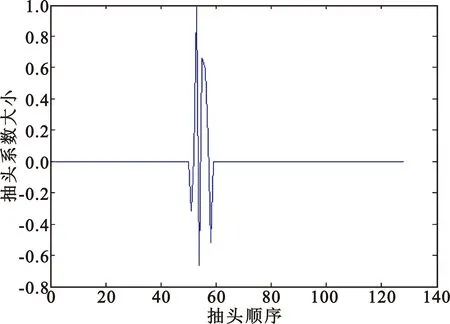
图4 随机产生抽头数为128个的稀疏语音信道

图5 高斯干扰环境下的语音信道识别
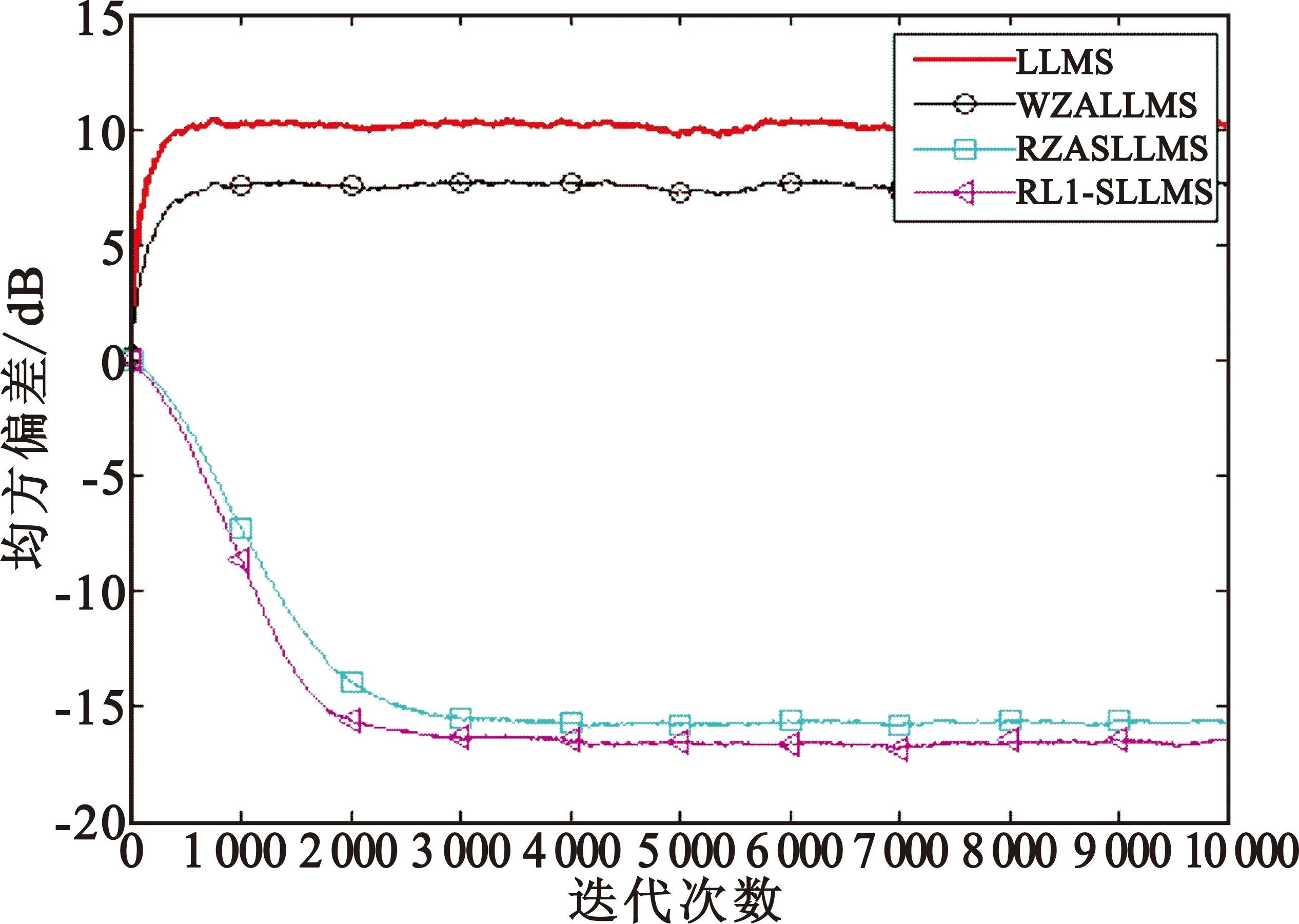
图6 非高斯干扰环境下的语音信道识别
从图5可以知道,在稀疏度较高的语音信道中提出的RZASLLMS、RL1-LLMS算法比现有的LLMS和 WZALLMS算法收敛更快。同时,从图6更可以看出提出的算法在非高斯干扰下的语音信道识别中有更强的健壮性。
6 结束语
本文针对传统的LLMS算法在识别稀疏系统时收敛速度慢的问题和不能抗冲激干扰的问题,首先利用两种不同的一范数加权因子对传统的LLMS算法的代价函数进行改进,使传统的LLMS算法具有稀疏识别性;然后又利用符号算法的思想对算法的迭代方程作进一步改进,使提出的算法具有抗冲激干扰的性能。由仿真结果得知,提出的两个算法的收敛性不仅在高斯干扰环境下明显优于LLMS算法,而且在噪声为非高斯冲激干扰环境中也明显优于LLMS算法和WZALLMS算法的收敛性能。因此,提出的RZASLLMS、RL1-SLLMS算法虽然牺牲了很小的计算复杂度,但是解决了LLMS算法不能识别稀疏系统的问题和WZALLMS算法不能抗冲激干扰的问题,具有很好的工程意义。下一步的研究工作是将本文提出的算法运用到冲激干扰环境下稀疏度时变的自适应系统识别问题中。
[1]HAYKIN S.Adaptive filter theory[J].Englewood Clilfs,NJ:Prentice Hall Co.,1991:231-238.
[2]叶挺,朱赛男.新变步长自适应算法及其时延估计性能[J].电讯技术,2014,54(6):775-779.
YE Ting,ZHU Sainan.A new variable step-size LMS adaptive filtering algorithm and its performance in time delay estimation[J].Telecommunication Engineering,2014,54(6):775-779.(in Chinese)
[3]FARHANG-BOROUJENY B.Adaptive filters:theory and applications[M].New York:John Wiley & Sons,2013:9-20.
[4]KADAGE M R,PATIL M S N.A new LMS for beamforming in mobile communication[J].International Research Journal of Engineering and Technology,2015,2(5):1-5.
[5]GITLIN R D,MEADORS H C,WEINSTEIN S B. The tap-leakage algorithm:an algorithm for the stable operation of a digitally implemented,fractionally spaced adaptive equalizer[J].Bell System Technical Journal,1982,61(8):1817-1839.
[6]DAS B K,CHAKRABORTY M. Sparse adaptive filtering by an adaptive convex combination of the LMS and the ZA-LMS algorithms[J].IEEE Transactions on Circuits and Systems I:Regular Papers,2014,61(5):1499-1507.
[7]SALMAN M S. Sparse leaky-LMS algorithm for system identification and its convergence analysis[J].International Journal of Adaptive Control and Signal Processing,2014,28(10):1065-1072.
[8]SALMAN M S,JAHROMI M N S,HOCANIN A,et al.A weighted zero-attracting leaky-LMS algorithm[C]//Proceedings of 2012 20th International Conference on Software,Telecommunications and Computer Networks(SoftCOM).Split,Croatia:IEEE,2012:1-3.
[9]PALEOLOGU C,BENESTY J,CIOCHINA S. Sparse adaptive filters for echo cancellation[J].Synthesis Lectures on Speech and Audio Processing,2010,6(1):34-36.
[10]SEO J H,JUNG S M,PARK P G. Proportionate sign subband adpative filtering algorithm for network echo cancellers[J].Journal of Advances in Computer Networks,2015,3(2):99-105.
[11]MAYYAS K A,ABOULNASR T. Leaky lms:a detailed analysis[C]//Proceedings of 1995 IEEE International Symposium on Circuits and Systems.Seatlle,Washington,USA:IEEE,1995:1255-1258.
[12]KAMENETSKY M,WIDROW B.A variable leaky LMS adaptive algorithm[C]//Proceedings of the Thirty-Eighth Asilomar Conference on Signals,Systems and Computers.Pacific Grove,CA:IEEE,2004:125-128.
[13]MAYYAS K,ABOULNASR T. Leaky LMS algorithm:MSE analysis for Gaussian data[J].IEEE Transactions on Signal Processing,1997,45(4):927-934.
[14]GUAN G,XU L,MA W,et al.Robust adaptive sparse channel estimation in the presence of impulsive noises[C]//Proceedings of 2015 IEEE International Conference on Digital Signal Processing(DSP).Singapore:IEEE,2015:628-632.
[15]CHEN Y,GU Y,HERO III A O. Sparse LMS for system identification[C]//Proceedings of 2009 IEEE International Conference on Acoustics,Speech and Signal Processing.Taipei:IEEE,2009:3125-3128.
[16]WU Z,PENG S,MA W,et al.Minimum error entropy algorithms with sparsity penalty constraints[J].Entropy,2015,17(5):3419-3437.
[17]SHI L,LIN Y.Convex combination of adaptive filters under the maximum correntropy criterion in impulsive interference[J].IEEE Signal Processing Letters,2014,21(11):1385-1388.

晏国杰(1989—),男,贵州铜仁人,现为硕士研究生,主要研究方向为稀疏自适应信号处理;
YAN Guojie was born in Tongren,Guizhou Province,in 1989. He is now a graduate student. His research concerns sparse signal processing.
Email:guojieyancqupt@foxmail.com
林云(1968—),男,四川南充人,现为副教授、硕士生导师,主要研究方向为压缩感知技术及稀疏信号处理。
LIN Yun was born in Nanchong,Sichuan Province,in 1968. He is now an associate professor and also the instructor of graduate students.His research concerns compressing sense and sparse signal processing.
Email:lycqupt@sina.com
Sparse Penalty Constraint Leaky Least Mean Square Algorithms against Impulsive Interference
YAN Guojie,LIN Yun
(Chongqing Key Laboratory of Mobile Communications Technology,Chongqing University of Posts and Telecommunications,Chongqing 400065,China)
The leaky least mean square(LLMS) adaptive filtering algorithm converges slowly when the identified system is sparse. Especially when the noise is non-Gaussian impulsive interference,the performance of LLMS algorithm deteriorates severely.To solve the problem that the convergent rate becomes slower because the system is sparse,the cost function of the conventional LLMS algorithm is improved by the two penalty functions,the reweighted zero-attracting(the log-sum penalty) and reweighted1-norm(RL1),respectively. To address the problem of the impulsive interference,the iterative functions are improved by introducing the sign function. Simultaneously,the simulations are made for the proposed algorithms to prove to be better performances compared with existing leaky-style algorithms in the case of impulsive interference.
sparse system identification;adaptive filtering algorithm;impulsive interference;convergence
10.3969/j.issn.1001-893x.2016.10.016
2016-01-15;
2016-04-18Received date:2016-01-15;Revised date:2016-04-18
TN912.3
A
1001-893X(2016)10-1153-06
引用格式:晏国杰,林云.抗冲激干扰的稀疏惩罚约束遗漏最小均方算法[J].电讯技术,2016,56(10):1153-1158.[YAN Guojie,LIN Yun.Sparse penalty constraint leaky least mean square algorithms against impulsive interference[J].Telecommunication Engineering,2016,56(10):1153-1158.]
**通信作者:guojieyancqupt@foxmail.comCorresponding author:guojieyancqupt@foxmail.com

