基于改进仿电磁学ELM在相机标定中的应用

王 琥，胡立坤，谭 颖

(广西大学电气工程学院， 广西南宁530004)



基于改进仿电磁学ELM在相机标定中的应用

王 琥，胡立坤，谭 颖

(广西大学电气工程学院， 广西南宁530004)

针对相机标定时难以建立精确的数学模型以及极限学习机(ELM)在隐层节点数少时逼近精度低的问题，提出了基于改进仿电磁学(EM)优化ELM的双目视觉相机标定方法。在标定过程中，采用极限学习机精确逼近图像坐标与世界坐标间的非线性关系，利用改进EM策略，包括使用自适应步长以及空间解收缩，优化ELM的输入权重和隐层偏置，提高ELM的收敛速度和泛化能力。实验结果表明，改进EM-ELM优化算法的收敛速度快于PSO的，且用更少的隐层节点数取得较高的标定精度。

相机标定；仿电磁学；极限学习机

0 引 言

相机标定是机器视觉中最底层且最关键的技术，标定技术的精确性决定机器视觉的效果。标定技术的主要原理是计算出相机的内部参数和外部参数，即二维图像信息与世界三维空间信息之间的映射关系。随着机器视觉被广泛应用于各行业，标定技术成了学者们的研究热点。如今的相机标定技术主要分为两大类，一类为直接式(显式)标定，另一类为间接式(隐式)标定。直接式标定方法主要有线性法、两步法[1]、改进两步法，张正友法[2]等，其主要过程是：在忽略高阶因素影响的前提下建立相机的数学模型，进而求解出模型中待解的未知参数。求解参数方法有最小二乘法、智能算法(如差分算法[3])逼近等。此类标定方法计算步骤比较繁琐，而且由于受到径向畸变和切向畸变参数的影响，其标定精度有所降低。间接式标定法主要有两类，一类为利用现有的智能算法，如BP算法[4]、神经网络算法[5-7]、支持向量机(SVM)算法[8]等逼近拟合二维图像信息和世界三维空间信息之间的关系；另一类为采用智能算法对神经网络算法进行优化，再用其逼近拟合二维图像信息和世界三维空间信息之间的关系。第二类方法可以避免测定相机复杂的几何模型和光学参数，故能够更大程度地提高相机的标定精度。文献[9]基于神经网络标定的基础上，利用智能算法(PSO)优化神经网络的权重与阈值，通过对比未优化神经网络方法的标定结果验证了此算法对于提高相机的标定精度的有效性。文献[10]在最小二乘支持向量机(LSSVM)回归的基础上，利用粒子群优化LSSVM，使LSSVM具有更好的泛化能力，同时提高相机的标定精度。文献[11]采用ELM对机械臂进行控制，验证了ELM泛化能力强于RBF。文献[12]采用ELM处理分类问题，证明了ELM训练速度高于SVM。

在隐式相机标定法中，评判算法的实用性的关键因素除标定精度外，更重要的是算法的效率和质量。在泛化能力上，SVM优于神经网络；在训练时间上，神经网络消耗的总时间明显低于SVM[13]。极限学习机(ELM)在保持强泛化能力的同时其消耗的总时间也较少，可以同时兼顾训练时间和泛化能力，是一种基于单隐层前馈神经网络学习方法。为了保持ELM的泛化能力和学习速度的同时减小系统的隐层节点数，本文提出了基于仿电磁学优化的极限向量机(EM-ELM)相机标定方法,利用ELM优良的非线性泛化能力，逼近二维图像坐标和世界三维空间坐标的映射函数，并使用仿电磁学算法优化ELM的输入权重以及阈值，从而达到高精度标定的目的。

1 基于EM的ELM算法

1.1 极限学习机(ELM)

极限学习机是黄广斌等[14]于2006年提出的一种基于前馈型单隐层神经网络的新型监督性学习算法。相比于传统的神经网络算法，极限学习机能够快速解析网络输出权值，从而降低计算量和搜索空间，使得神经网络的学习速度和泛化能力得以提高，因而具有很强的非线性逼近能力。极限学习机的网络模型可表示为：

(1)

式中，N为隐层节点数，βi为连接隐层和输出层的输出权值，g为激励函数，ωi为连接输入层和隐层的输入权值，bi为隐层的偏置(阈值)，oj为网络的输出，M为训练的样本数。

(2)

令：

(3)

则式(2)可改写为矩阵形式，即：

Hβ=Y，

(4)

式中，Y为期望输出向量，H为ELM的隐层输出矩阵。

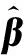
(5)

式中，H+为H的Moore-Penrose广义逆。因此，ELM的训练过程如下：

Step 1 选取隐层节点数和激励函数，随机设定输入层权值以及偏差；

Step 2 计算隐层输出矩阵H；

1.2 仿电磁学算法(EM)

EM算法[15]由Birbil和Fang于2003首次提出，是一种模拟电荷间的排斥和吸引作用的计算优化技术。仿电磁学算法由于自身具备记忆和反馈的特点，能够避免算法的搜索迂回，从而提高了算法的收敛速度。仿电磁学算法(EM算法)和PSO算法都属于并行处理算法，但EM算法的收敛速度更快。

仿电磁学算法的搜索原理：随机产生符合优化目标函数的带电粒子群，带电粒子通过动力方程式进行迭代更新，以适应度为依据判定带电粒子的优劣，从而求解出个体最优值和全局最优值。动力方程式为：

(6)

其中，

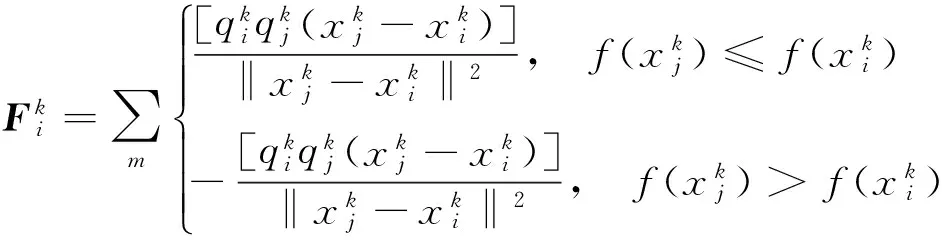
1.3 改进EM

基本的EM算法主要分为三个步骤，即局部搜索、适应度评价、更新粒子。为了精简局部搜索步骤，借鉴文献[16]，通过使用自适应迭代步长代替耗时较长的局部搜索，即前期搜索采用较大步长，当出现评价指标停止不前次数达到8次的时候，按式(7)对迭代步长进行缩减，即：

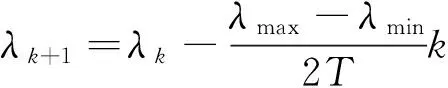
(7)

式中，T为总迭代次数，k为当前迭代次数。

搜索空间的大小势必影响搜索的进度，为了达到快速搜索最优解，搜索空间同时按照式(8)、式(9)进行调整。

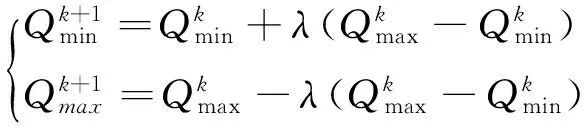
(8)

(9)

式(9)中，Qbest为当前最优解空间。

1.4 EM优化ELM算法

当ELM的隐层节点数与训练样本数一致时，ELM才能以零误差逼近样本。然而，在实际应用中，ELM的隐层节点数远远低于样本数，因此，ELM的逼近精度有所下降。为了能在提高精度的同时使用较少的隐层节点数来逼近训练样本。本文使用仿电磁学算法对ELM的输入权值和隐层节点偏置(阈值)进行寻优。

解域的确定：ELM的输入权值和隐层节点偏置的取值范围为[-1,1]，因此，带电粒子解域范围为[-1,1]。

EM优化ELM的学习流程：

Step 1 导入训练样本，即包括摄像头获取的图像二维坐标和世界三维空间坐标的样本，同时，对所有样本进行归一化处理。

Step 2 建立EM-ELM神经网络结构，主要包括设定神经网络的隐层节点数和激活函数。一般激活函数选择S(sigmoid)函数。

Step 3 初始化EM参数，包括待优化参数(输入权值、偏置)的带电粒子个数、初始电荷量、最大迭代步数以及终止条件等参数。初始电荷量范围为粒子解域范围即[-1,1]。

Step 4 计算每个带电粒子的适应度。优化的目的在于提升神经网络的逼近能力和精度，因此，适应度优化目标函数选取为三维空间坐标的实际输出和期望输出的均方根误差，即ELM输出的测试误差值，即：

(10)

其中，XR,YR,ZR代表网络实际输出的三维坐标信息，XE,YE,ZE代表实际标定测量的三维坐标信息。

Step 5 根据EM的动力方程式(6)进行带电粒子的更新。

Step 6 判断是否达到终止条件(最大迭代步数或精度要求)，否则进入Step 4继续搜索。

2 标定实验

2.1 实验样本的获取

图1 标定板Fig.1 Calibration board

极限学习机的输入样本为双目相机获取的左右图像坐标[ul,vl],[ur,vr]。为了提高精确度，世界坐标的标定采用电控三维精密平台，输出的样本为标定在世界坐标下的坐标，即[XE,YE,ZE]。实验用的双目摄像头采用深圳显微公司生产的CCD摄像头，其分辨率为1600×1200。标定板采用如图1所示的圆形标定板。标定板采用12×12的圆点方阵，相邻两圆点的实际距离为10.0 mm，标定点即为每个黑圆点的圆心。通过电控三维精密平台的平移，在不同的方位拍摄6对图像(如图2所示)即为拍摄后的一对标定图。而后,使用MATLAB平台对获取的图像进行图像处理，包括图像增强、去噪、边缘检测、利用霍夫变换提取圆心所在的图像坐标信息。由于相机同处于一水平线，因此左右图像圆心在阵列位置一一对应匹配于标定板的阵列相应位置，即双目匹配。总共提取864标定点，训练样本采用5对图像组，即720个标定点，其余的144个标定点作为测试样本。

(a) 左图像

(b) 右图像

图2 标定图像

Fig.2 Calibration image

2.2 ELM的训练优化

设定ELM神经网络的输入节点为4个，隐层节点数为6，输出节点为3个，结构图如图3所示，迭代最大次数为T=100，种群个数为25，激励函数为S函数。由于受S函数灵敏区限制，样本按式(11)归一化处理，即：

x′=(x-xmin)/(xmax-xmin)，

(11)

优化适应度函数采用式(10)为依据，误差越小，优化精度越高。

2.3 实验结果与分析

仿真平台为MATLAB 2014a，PC处理器为Intel(R) Core(TM) i5-3470 @3.2 GHz。为了可以有效地进行对比，本研究共进行3组实验，分别为ELM，PSO-ELM和EM-ELM。

为了进行有效比较，PSO参数的设置与EM一致，即设定输入节点为4，隐层节点数为6，输出节点为3，迭代最大次数为T=100，种群个数为25，粒子位置与速度的范围为[-1,1]，优化适应度函数采用式(10)。

未使用优化方法的ELM，经过多次实验，可得如图4所示的结果，误差的计算采用式(10)。从图4中可见，由于阈值和输入权重是随机的，因此，每次运行结果所得测量误差有所不同，测量误差值的波动范围为[15，70]。

图3 ELM神经网络结构

Fig.3 Structure of ELM neural network

图4 第P次拟合与误差的关系

Fig.4 Relation betweenPth training and error

经过优化后的ELM算法不仅可以降低测量误差，同时也减小误差的波动。最大迭代步数与误差关系如图5所示，可见，当迭代步数增加时，逼近误差随之下降，收敛至一定的数值。表明粒子群算法和仿电磁学算法在优化极限学习机的泛化能力是可行的、有效的，且标定精度有所提高。EM-ELM算法在迭代次数达到12次左右，其误差收敛到最小，而PSO-ELM算法在迭代次数达到40左右才收敛，表明基于仿电磁学的极限学习机标定的收敛速度更快。由于粒子群算法无记忆和反馈特性，在此类优化上容易陷进局部最优，因此，在第20～35迭代过程中出现了停滞，陷入局部最优，且PSO在相同隐层节点数下训练100次的总耗时比EM的多，如表1所示。

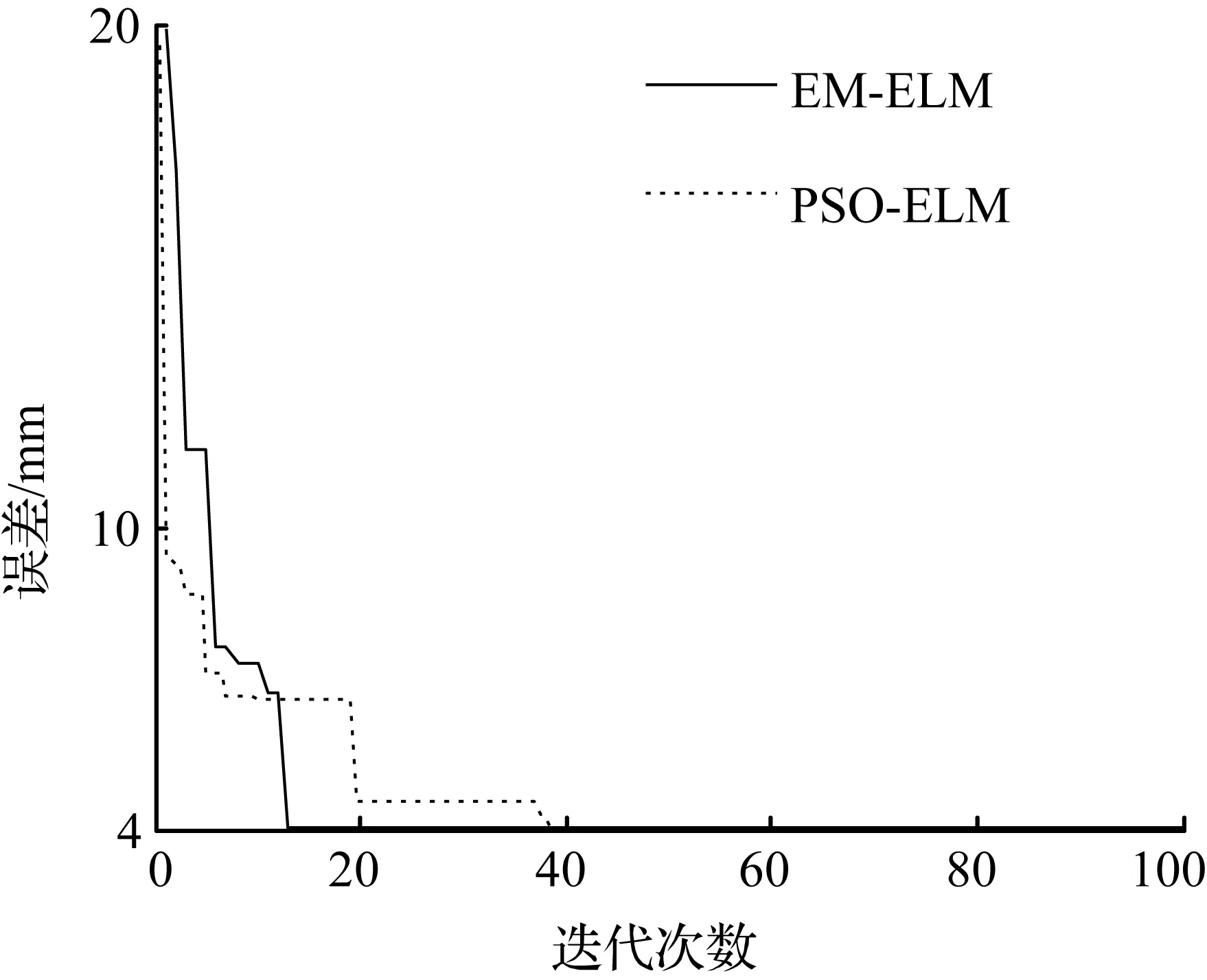
图5 迭代次数与误差的关系Fig.5 Relation between interaction and error

隐层节点数PSO/sEM/s322.6721.75622.8821.95923.3922.431123.7522.662225.8723.924027.6226.02

通过选取不同的隐层节点数，对比ELM、PSO-ELM和EM-ELM算法的逼近误差，训练100次可得如表2所示的结果。由表2可知，隐层节点数越少，极限学习机的逼近能力越差，极限学习机只能单纯通过提高隐层节点数来提高逼近精度，而仿电磁学或PSO优化后的极限学习机可以在同等的隐层节点数下在一定程度上提高极限学习机的逼近精度。

表2 ELM与EM-ELM的测量误差

图6 视觉系统平台Fig.6 Vision system platform

为了验证其精确性和实用性，结合EM-ELM算法、CCD双目摄像机，以及电控平台构成如图6所示的系统进行验证。由PC端的MATLAB软件对CCD相机进行图像采集控制和图像处理，将检测到的图像坐标输入至EM-ELM网路中，计算出目标物体在世界坐标系[XE,YE,ZE]的位置。

表3 不同隐层节点数EM-ELM测量值

通过三维电控平台测3组不同的数据，第一组：A=[XE1,YE1,ZE1]=[140,60,150]；第二组：B=[XE2,YE2,ZE2]=[60,140,50]；第三组：C=[XE3,YE3,ZE3]=[0,80,100]；将3组数据作为真实值，由标定好的CCD双目相机获取图像坐标。采用经过训练优化后的网络对图像获取的数据进行计算，得出测量值。真实值与测量值如表3所示。由表3可见，随着隐层节点数增加，误差可控在1 mm内，计算所需的时间较小，优化后的网络应用在机器视觉伺服回路中的延迟干扰不大，可满足机器视觉要求。

通过以上实验以及分析可知：优化后的网络在同样的精度要求下所需的隐层节点数较少；当隐层节点数达到11个左右，优化后的网络误差在1 mm以内。当训练数据采用的是基于摄像机坐标系下的数据，则只要左右相机的相对位置不变，训练好的网络计算结果是基于相机坐标系的，因此有利于移植双目相机应用于别的场合。但此标定策略仅限制于小范围空间的标定，如点焊机器人、臂展较短的工业机器人作业等小范围高精度场所。

3 结 语

本文提出了基于仿电磁学算法优化下的极限学习机相机标定方法，采用改进EM优化ELM的输入权重和隐层偏置，提高了ELM的收敛速度和泛化能力。优化算法的收敛速度比PSO更快，标定精度更好，并有效解决了相机标定中由于建模不准确如不考虑非线性项等因素而带来的误差，以及当隐层节点数较少时ELM逼近精度不够的问题。

[1] TSAI R Y.A versatile camera calibration technique for high-accuracy 3D machine vision metrology using off-the-shelf TV cameras and lenses[J]. IEEE Journal on Robotics & Automation, 1987, 3(4):323-344.

[2] ZHANG Z Y.A flexible new technique for camera calibration[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2000, 22(11): 1330-1334.

[3] 李国进,李占海,陈双,等.基于差分演化算法的摄像机高精度标定[J]. 广西大学学报(自然科学版), 2014,39(2):387-392.

[4] 李晶，袁峰，丁振良.基于BP神经网络的外姿态测量系统线阵CCD标定[J]. 仪器仪表学报, 2010, 31(5):1138-1141.

[5] CHEN B, WANG W, QIN Q.Stereo vision calibration based on GMDH neural network.[J]. Applied Optics, 2012, 51(7):841-845.

[6] 宗晓萍，徐艳，郝雷.基于神经网络的视觉伺服机器人摄像机标定[J]. 仪器仪表学报, 2006, 27(z1): 814-816.

[7] AHN B, PARK J, KWEON I S.Real-time head orientation from a monocular camera using deep neural network[J]. Lecture Notes in Computer Science, 2015, 9005:82-96.

[8] 刘胜,傅荟璇,王宇超.基于分割区间LS-SVM的摄像机标定[J]. 计算机工程, 2009, 35(24):179-181.

[9] 周东凯,李刚,王学琨.基于PSO-ELM的双目视觉摄像机标定[J]. 广西大学学报(自然科学版), 2014,39(6):1285-1290.

[10]刘金颂，原思聪，江祥奎,等 基于PSO和LSSVM回归的摄像机标定[J]. 光电工程, 2010, 37(5): 47-51.

[11]乃永强，李军.基于极限学习机的机械臂自适应神经控制[J]. 信息与控制, 2015, 44(3):257-262.

[12]RONG H J, ONG Y S, TAN A H, et al.A fast pruned-extreme learning machine for classification problem[J]. Neurocomputing, 2008, 72(13): 359-366.

[13]申丰山，王黎明，张军英.基于SVM技术的精简极速学习机[J]. 华中科技大学学报(自然科学版), 2014,42(6): 107-110.

[14]HUANG G B, ZHU Q Y, SIEW C K.Extreme learning machine: Theory and applications[J]. Neurocomputing, 2006,70(1-3): 489-501.

[15]BIRBIL S, FANG S C.An electromagnetism-like mechanism for global optimization[J]. Journal of Global Optimization, 2003, 25 (3): 263-282.

[16]吴杰康，郭壮志.基于仿电磁学算法的梯级水电站多目标短期优化调度[J]. 中国电机工程学报, 2010,30(31): 14-21.

(责任编辑 裴润梅)

Application of ELM via improved electromagnetism-like mechanism in camera calibration

WANG Hu, HU Li-kun, TAN Ying

(College of Electrical Engineering, Guangxi University, Nanning 530004,China)

Due to the difficulties of establishing accurate mathematical model for camera calibration and low approximation accuracy by using extreme learning machine (ELM) with less hidden layer node, a binocular vision calibration method that ELM with improved electromagnetism-like mechanism(EM) is proposed. The ELM model is used to describe the non-liner relation between the stereo image point and the 3D geometry while the improved EM with space reduction and self- adaptive steps is used to optimize the input weights and hidden layer bias of ELM. Then the convergence speed and generalization ability of ELM are improved. The experimental results show that the improved EM-ELM algorithm has faster convergence speed than PSO, and better calibration accuracy with fewer hidden layer nodes.

camera calibration; electromagnetism-like mechanism; extreme learning machine

2016-05-03；

2016-05-25

广西自然科学基金资助项目(2012GXNSFBA053144)

胡立坤(1977—)，男，湖北襄樊人，广西大学教授，博士;E-mail：hlk3email@163.com。

王琥，胡立坤，谭颖.基于改进仿电磁学ELM在相机标定中的应用[J].广西大学学报(自然科学版)，2016，41(5)：1500-1507.

10.13624/j.cnki.issn.1001-7445.2016.1500

TP391

A

1001-7445(2016)05-1500-08