千佛崖组复杂致密砂岩储层参数计算方法研究

程 丽 冯明刚 王 昆 李素兰

（中国石化勘探分公司研究院，四川 成都 610041）

千佛崖组复杂致密砂岩储层参数计算方法研究

程 丽 冯明刚 王 昆 李素兰

（中国石化勘探分公司研究院，四川 成都 610041）

千佛崖组储层主要发育低孔、低渗致密储层，储层岩石类型及储集空间类型复杂，且储层流体性质多样，导致精确计算储层岩石矿物组分及物性参数面临困难。通过岩心刻度测井资料，针对不同岩性及不同类型储层，形成了基于岩石物理体积模型和多参数数理统计分析为基础的孔隙度计算模型；建立了以岩心孔渗关系为基础的渗透率计算模型；明确了千佛崖组地层岩电参数及地层水参数取值，建立了适合本区千佛崖组的饱和度计算方法。将所建模型计算的储层参数与岩心分析数据进行对比分析表明，测井计算精度较高，能够满足该区储层参数计算的精度要求。

复杂致密砂岩 储层类型 储层参数计算 千佛崖组

0 引言

千佛崖组主要为滨浅湖—三角洲沉积环境，地层以泥页岩为主，局部发育细—粉砂岩、粉砂质泥岩、炭质泥岩等。储层主要发育于千佛崖组二段致密砂岩段，储层岩石类型复杂，包括岩屑长石砂岩、岩屑石英砂岩和粉砂岩等，孔隙类型主要为粒间黏土矿物晶间微孔隙和长石粒内溶孔。岩心物性资料分析表明孔隙度在0.9%～7.2%，平均孔隙度为3.5%，渗透率为0.001～2.65 mD，为低孔低渗致密砂岩储层。近年来，继元坝地区X9井在千佛崖组测试获得工业油气流之后，川东北元坝、川东南涪陵区块中多口井在侏罗系千佛崖组（凉高山组）地层钻遇良好油气显示，目前在巴中和涪陵地区部分井又测试获得工业油气流，展示了千佛崖组地层良好的勘探前景［1-3］。为满足勘探生产及储量参数研究需要，本次研究选取巴中地区具有丰富取心资料的关键井，利用岩心刻度测井资料，通过地质与测井相结合的方法，对千佛崖组致密砂岩储层参数进行敏感性分析及数理建模，优选出适合千佛崖组储层参数计算的模型。综合分析认为，本次研究所建模型计算得出的储层参数与岩心分析数据较为吻合，计算精度满足《石油天然气储量计算规范（DZ/T0217-2005）》的要求，有力地支撑了勘探生产工作。

1 储层类型

根据常规测井与FMI成像测井资料分析认为，千佛崖组储层主要分布在千二段岩屑砂岩及油气显示活跃的泥岩段。储层岩性以细—粉砂岩、泥质粉砂岩和粉砂质泥岩为主。按照储层的岩性组合特征可将储层分为孔隙型储层、裂缝—孔隙型储层、裂缝型储层以及泥岩裂缝型储层。

孔隙型储层。岩性以细砂岩为主，基质孔隙较发育，裂缝不发育。其在电测曲线呈低自然伽马值（43～65 API）、低密度（2.52～2.65 g/cm3）、相对高中子（5%～18%）、相对高声波时差（大于55 μs/ft）、相对低电阻率（70～450 Ω·m）块状基质孔隙储层特征。

裂缝—孔隙型储层。岩性主要为细砂岩，储层类型以孔隙型为主，局部有裂缝发育。其电测曲线呈中—低自然伽马值（小于50 API）、低密度（2.48～2.64 g/cm3）、高中子（5%～10%），高声波时差（54～70 μs/ft）、相对低电阻率（100 Ω·m左右）特征。其中声波时差伴有一定跳波现象；双侧向电阻率局部有一定差异；FMI成像图可见裂缝特征。

裂缝型储层。岩性主要为细—粉砂岩，常规测井及偶极声波衰减变密度图可见裂缝特征明显。电测曲线呈中低自然伽马值（45～70 API）；三孔隙度曲线与电阻率曲线呈尖刺状特征，且对应性较好。其中声波时差明显增大（75～98 μs/ft），密度相应降低（2.43～2.65 g/cm3），中子相应增大（13%～35%）；电阻率值为相对低阻特征，裂缝发育段在斯通利波衰减变密度图上可见明显的“人字形”干涉条纹。

泥岩裂缝型储层。岩性主要为粉砂质泥岩、泥岩。电测曲线呈中高自然伽马值（60～90 API）；声波时差明显增大，密度相应降低，中子相应增大；电阻率值在高骨架值背景下呈块状降低特征；当裂缝发育时，声波时差明显跳跃增大；裂缝较发育。

2 测井建模的技术方法

针对千佛崖组致密砂岩储层，主要采用两种方法建模：一种是以地质资料为基础，首先对岩心、薄片以及钻、录、测井资料进行分析，开展四性关系研究，通过测井曲线敏感性分析法，优选出与储层参数相关性较好的测井曲线，并以此进行数理拟合建立区域性经验公式；另一种是在测井岩石矿物模型和体积模型的基础上，结合地质特征和测试资料情况完善解释模型参数，建立响应方程式来求储层参数。最终运用两种方法建立的不同测井解释模型对研究区关键井进行常规测井资料精细处理，并结合岩心分析资料对处理结果进行对比分析，优选出最合适的测井解释模型。

3 储层参数计算

3.1 测井资料分析

巴中地区千佛崖组地层的测量项目较齐全井有6口井，其中取心井有3口，取心收获率均为100%。在利用岩心刻度测井数据建立储层参数计算模型前，根据小岩心样分析密度值与测井密度曲线的对应关系，结合岩性描述资料对取心井进行岩心归位，以确保本次研究所建模型的可靠性。具体资料情况见表1。总体而言，测井及岩心资料较为丰富，能够满足储层参数建模及参数计算精度分析的要求。

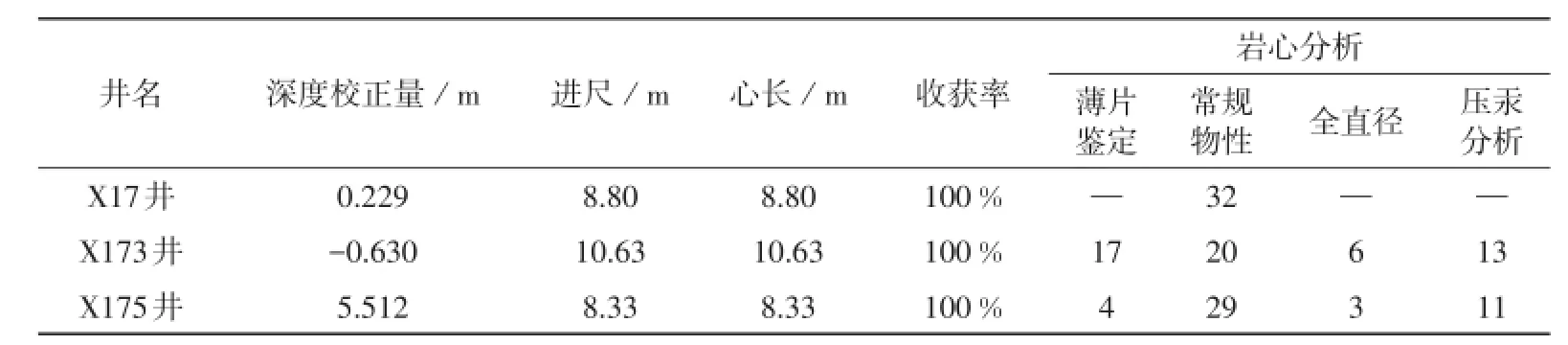
表1 研究区千佛崖组（凉高山组）钻井取心及分析化验资料统计表

3.2 孔隙度计算

千佛崖组储层类型多样，不同岩性不同储层类型的储集层需根据具体情况选择合适的孔隙度计算模型。细砂岩 — 粉砂岩类裂缝型储层和泥岩裂缝型储层由于受裂缝影响，常规测井曲线计算的孔隙度不能完全反映储层孔隙大小，一般结合成像测井进行半定量评价［4］。因此笔者仅针对细砂岩类基质孔隙发育的孔隙型储层进行孔隙度计算。主要通过岩心刻度常规测井资料，进行敏感性参数分析，采用多参数数理统计分析及岩石物理体积模型［5］来优选孔隙计算模型。

3.2.1 敏感性参数分析

千佛崖组细砂岩类孔隙型储层基质孔隙储层发育，三孔隙度曲线中，岩性密度曲线与岩心孔隙度相关性最好，相关系数为0.847；因此，针对细砂岩类孔隙型储层可采用密度体积模型和将岩性密度作为敏感参数通过拟合法进行数理建模，确定对应细砂岩地层孔隙度计算模型。

3.2.2 数理统计建模

采用三孔隙度曲线（岩性密度、声波时差、补偿中子）与岩心孔隙度的线性相关关系可建立研究区敏感参数拟合法计算孔隙度公式为：

式中，POR为密度孔隙度，%；ω（X）为敏感曲线测井值；a、b为地区经验参数。

考虑到不同地区岩性密度不仅与地层孔隙度大小有关，其特征值大小还受地层泥值含量等其他地层参数影响，拟合建模公式中参数a、b各不相同，利用拟合数理建模法计算的孔隙度没有考虑不同地区泥质及矿物成分的影响，不能完全反映地层特征，局限性较强，适用性较差。

3.2.3 岩石物理体积模型

千佛崖组细砂岩类孔隙型储层采用岩性密度体积模型，排除泥质的影响，其计算细砂岩地层孔隙度计算精度较高（式2）。而对于泥质含量较高的粉砂岩地层该模型应用效果较差，采用声波时差体积模型计算精度较高（式3）。

体积密度计算孔隙度公式：

式中，PORD为密度孔隙度，%；DEN、Dgma分别为密度测井值、岩石密度骨架值；Df、Dsh分别为流体密度值及泥岩密度测井值；Vsh为泥质含量，%。

声波时差计算孔隙度公式：

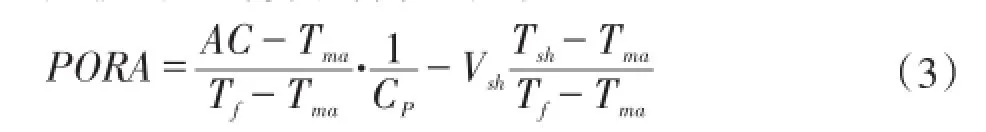
式中，PORA为声波孔隙度，%；AC、Tma分别为声波时差测井值、岩石声波骨架值；Tf、Tsh分别为流体声波时差值、泥岩声波时差值，μs/ft；CP为压实校正系数。

3.3 渗透率计算

地层渗透率是指岩层在一定压差下流体的渗流能力。它是评价油层好坏的重要指标之一。渗透率主要受到粒度中值、黏土含量、孔隙度和束缚水饱和度等地质因素的综合影响［5-6］，目前较为常用的渗透率计算方法是Timur公式和岩心孔渗关系法。其中，Timur公式主要是根据孔隙度和束缚水饱和度来确定；岩心孔渗关系法是通过分析岩心渗透率与其主要影响因素的关系来建立区域性的渗透率计算模型，计算公式及其经验参数随研究区域不同有所差异。针对研究区千佛崖组地层特点，分别采用孔隙度和束缚水饱和度法（Timur公式）和数理建模法进行渗透率计算研究。

3.3.1 孔隙度和束缚水饱和度确定渗透率

影响渗透率的主要地质因素中，孔隙度与束缚水饱和度的影响情况相反：岩石比表面越大，即表明其孔隙越小，孔隙结构越复杂，孔隙表面对流体流动的阻滞作用越大，渗透率越小。因此，孔隙度和束缚水饱和度这种相关关系可以确定渗透率，较为常用的即Timur公式（式4）：

式中，Swb为束缚水饱和度，%；φ为孔隙度，%；K为绝对渗透率，mD；C为地区经验参数，一般取0.136。

3.3.2 岩心分析资料建立渗透率计算模型

该渗透率模型建立在岩心物性分析的基础上，通过岩心渗透率与岩心孔隙度交会分析，采用数理建模计算公式作为储层渗透率的计算模型。不同地区的经验公式及参数各不相同，该方法仅针对区域有岩心分析资料的情况可采用关键因素进行数理建模，形成经验计算模型。

图1为X17、X173以及X175井千佛崖组细砂岩孔隙型储层岩心孔隙度与岩心渗透率交会图，从图1可知，渗透率为0.006～0.087 mD，储层渗透率主要分布在0.001～0.087 mD。其相关关系如下：

式中，y为渗透率，mD；x为孔隙度，%；R为相关系数。

图1 X17、X173以及X175井千佛崖组细砂岩孔隙型储层岩心孔隙度与岩心渗透率交会图

3.4 应用效果检验

3.4.1 孔隙度计算成果检验

细砂岩类孔隙型储层以基质孔隙为主，岩石类型及矿物含量变化较小，岩性对密度测井值的影响相对稳定，在井眼条件较好的情况下密度曲线一定程度上主要反映地层孔隙发育情况，因此针对千佛崖组细砂岩类孔隙型储层采用密度体积模型（式2）计算的地层孔隙度精度较高，能够满足《石油天然气储量计算规范（DZ/T0217-2005）》的要求。

图2 X173井细砂岩类孔隙型储层段测井孔隙度与岩心孔隙度对比分析图

如图2为X173井细砂岩类孔隙型储层段测井孔隙度与岩心孔隙度对比分析图，其中测井计算孔隙度与岩心孔隙度大小及变化趋势相符，仅局部有4个岩屑砂岩样点的孔隙度与测井孔隙度匹配性较差，其对应自然伽马高值，测井计算孔隙度受岩性和泥质含量影响，可将其视为奇点。去掉奇点后的测井孔隙度与岩心孔隙度交会图显示相关性较好，相关系数为0.865。同理X17井细砂岩孔隙型储层采用密度体积模型计算的孔隙度精度较高，与岩心孔隙度相关系数为0.936。

在泥质含量相对较高的粉砂岩、泥质粉砂岩地层，局部容易出现井扩现象，此时密度曲线受影响较大，而声波时差曲线受井眼条件影响较小，且在千佛崖组泥质粉砂岩地层与岩石颗粒及泥质含量响应较为敏感，一定程度上可以反映地层岩性及孔隙特征。应用声波体积模型处理计算该类地层孔隙度与岩心孔隙度较吻合，可以满足研究区解释精度的要求。

图3为F4井泥质粉砂岩地层测井孔隙度与岩心孔隙度对比分析图，图3a为F4井千佛崖组泥质粉砂岩类低孔地层测井解释成果图，由图3a可以看出，测井计算孔隙度与岩心孔隙度整体上较为吻合，仅局部裂缝相对发育，去掉受裂缝影响较大2个岩样点后，测井孔隙度与岩心孔隙度整体相关性较好。如图3b测井孔隙度与岩心孔隙度交会图显示，相关系数R达到0.845，能够满足孔隙度计算精度的要求。

3.4.2 渗透率计算成果检验

图4为X175井通过岩心拟合方法（式5）建立的新模型计算的渗透率精度分析图与采用常规渗透率Timur公式（式4）计算的渗透率精度对比分析图。其中，Timur公式在千佛崖组致密砂岩地层应用效果较差，计算渗透率的精度较低，仅能达到反映储层渗透率变化趋势的程度。分析其原因可知，研究区千佛崖组地层非均质性较强，储层具有复杂性，影响渗透率的因素众多，尤其局部裂缝的发育对渗透率的影响较大。而Timur公式主要是根据孔隙度和束缚水饱和度来确定渗透率，该计算模型难以囊括所有的影响因素。而运用岩心数据拟合方法新建的渗透率计算模型处理精度可以得到明显提高，该方法能够较为客观地反映页岩在地下的真实渗透率特征。需要注意的是岩心孔渗关系法计算得到的渗透率主要表征基质渗透率，裂缝对储层渗透率的影响仍难以确定，但在孔隙型储层应用该方法进行渗透率估算，效果相对较好。

图3 F4井泥质粉砂岩地层测井孔隙度与岩心孔隙度对比分析图

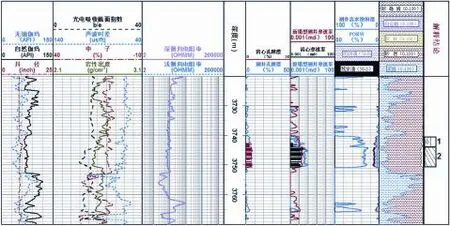
图4 X175井千佛崖组新老模型计算的渗透率对比图

根据计算成果统计，X175井细砂岩孔隙型储层岩心分析渗透率平均值为0.016 mD，测井计算的渗透率平均值由原渗透率模型计算的0.245 mD，变为0.017 mD。多口井处理成果表明，新建立的渗透率模型能更好地反映储层渗透率情况。

4 结论

千佛崖组岩性复杂、非均质性较好，岩石颗粒变化直接影响储层特征参数计算模型，分岩性建立孔隙度、渗透率计算模型，大幅提高了孔隙度、渗透率的计算精度，能够有效解决千佛崖组储层参数的计算难题。

1）孔隙度计算方面。细—粉砂岩类孔隙型、裂缝—孔隙型储层用体积密度模型计算孔隙度精度高；泥质含量较高的泥质粉砂岩类地层采用声波时差模型处理地层岩性及孔隙性效果较好；裂缝型储层及泥岩裂缝型储层需结合岩心、FMI成像、偶极声波等特殊资料综合定性识别和半定量评价。

2）渗透率计算。研究认为致密砂岩渗透率计算采用孔隙度和束缚水饱和度关系应用效果较差，运用岩心分析的岩屑砂岩孔隙度与渗透率建立模型计算效果较好；对于涪陵地区泥质含量较高的地层由于渗透率分布规律差，不可采用该方法。

［1］蒋裕强，漆麟，汪泽成，等.四川盆地侏罗系油气成藏条件及勘探潜力［J］.天然气工业，2010，30（3）：22-26.

［2］郭彤楼，李宇平，魏志红.四川盆地元坝地区自流井组页岩气成藏条件［J］.天然气地球科学，2011，22（1）：1-7.

［3］张闻林，陈义才.川西北部地区侏罗系气藏成藏特征［J］.天然气工业，2007，27（10）:15-19.

［4］吴兴能，刘瑞林，雷军，等.电成像测井资料变换为孔隙度分布图像的研究［J］.测井技术，2008，32（1）：53-56.

［5］雍世和，张超谟.高等学校教材：测井数据处理与综合解释［M］.山东：中国石油大学出版社，2007.

［6］洪有密.测井原理与综合解释［M］.北京：中国石油大学出版社，2008.

（编辑：卢栎羽）

B

2095-1132（2016）05-0010-05

10. 3969/j. issn. 2095-1132. 2016. 05. 003

修订回稿日期：2016-09-06

程丽（1985-），女，硕士，工程师，从事测井解释及储量研究工作。E-mail：colfigo@sina.com。