n维超平形体的体积比

英起志

（江苏商贸职业学院，江苏南通226011）

n维超平形体的体积比

英起志

（江苏商贸职业学院，江苏南通226011）

文章给出了n维超平形体体积比的计算公式，得出了它的渐进性质，并计算了部分超平形体的体积比。

n维超平形体；正方体；John椭球；体积比；渐进性质

在Rn中，我们通常把含有非空内点的紧致凸集称为凸体，多胞形（polytope）是一类基本的凸体，它是由有限个超平面围成的凸体。而n-超平形体（n-dimensionalparallelotope）是一种特殊的多胞形，它是2维平行四边形、3维平行六面体到高维空间的推广，后者可以分别叫做2-parallelotope和3-parallelotope，超矩形（orthotope）和超正方体（hypercube）都是特殊的超平形体。

凸体的体积比是凸体的重要特征之一，Rn中凸体K的体积比vr（K）定义为

其中ε是包含于K的椭球，vn（K）和vn（ε）分别表示K和ε的体积。1948年，Fritz John在著名的John椭球定理中证明了对于Rn中的任意凸体都包含体积最大的椭球，被称为凸体的John椭球。R Howard在文献［1］中证明了凸体的John椭球是唯一的。如果一个凸体的John椭球是欧氏单位球，则称该凸体处于“John位置”，任何凸体都可以在仿射变换的作用下使之处于John位置。R Howard在文献［1］中还证明了对于中心对称的凸体Cn，存在椭球E（Cn的John椭球），使得

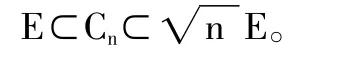
有了John椭球的概念，Rn中凸体K的体积比可以重新定义为

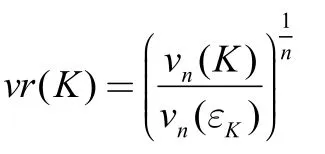
其中εK为凸体K的John椭球。仿射不变性是凸体体积比的重要性质。

引理1设Pn为n维超平形体，则其体积比

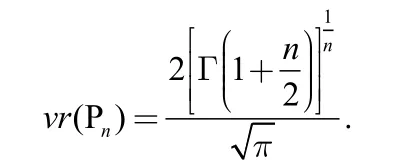
证明不失一般性，设n维超正方体Qn=［-1，1］n，Qn是一个中心在原点，边长为2的n维超正方体，其体积vn（Qn）=2n。Qn的 John椭球为Rn中的欧氏单位球，记为体积比的仿射不变性，vr（Pn）=vr（Qn），又

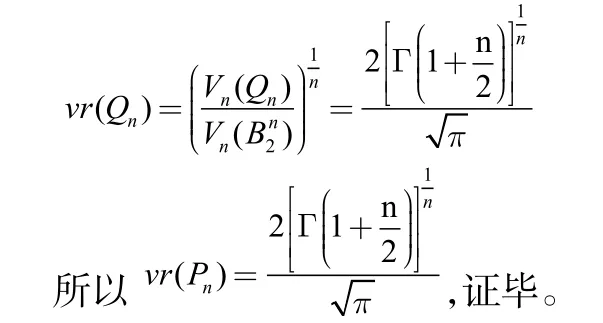
Keith Ball在文献［2］中证明了对于Rn中的所有中心对称凸体，n维超正方体的体积比最大。因此，对于Rn中的任意中心对称凸体cn，有。

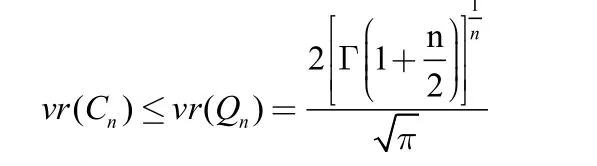
由体积比的仿射不变性，利用引理1可以求出任意维超平形体（包括超矩形、超正方体）的体积比。此外，结合体积比的定义，在已知超平形体的体积的条件下，可以求出其John椭球的体积。

定理1设Pn为n维超平形体，则当n→+∞时，vr（Pn）→+∞，且随着n的增加，vr（Pn）是严格单调递增的。

证明由引理1和Stirling公式（当t→+∞时，Γ（1+t）～

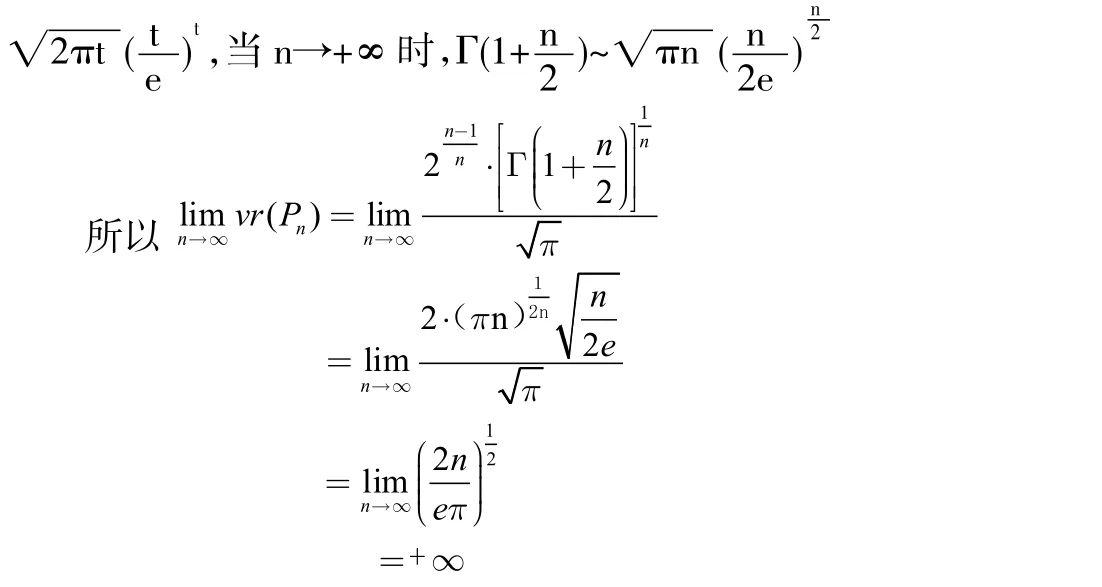
所以1997年，G.D.Anderson和S.-L.Qiu证明了函数f（x）=）上单调递增，2006年，张素玲等在文献［3］中将该函数的单调递增区间扩展到（0，+∞）。下面利用这一重要性质，证明当n增加时，vr（Tn）是严格递增的。

把vr（Pn）看作是关于n的函数，不难发现，当n＞4时，它是单调递增的。又通过计算易知vr（P1）＜vr（P2）＜vr（P3）＜vr（P4）。因此，对任意的正整数n，（Pn+1）＞vr（Pn），证毕。

部分n维超平行体的体积比的值见表1。

［1］R Howard.The John ellipsoid theorem［J］.University of South Carolina，1997.

［2］Keith Ball.Volume ratios and a reverse isoperimetric inequality［J］.Journal of the London Mathematical Society，1991，44:351-359.

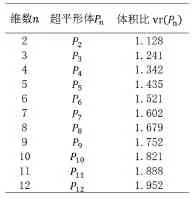
表1　超平行体的体积比（保留3位小数）

［3］张素玲，陈超平，等.关于伽玛函数的单调性质（英文）［J］.大学数学，2006（04）：50-55.

［4］Keith Ball.Ellipsoids of maximal volume in convex bodies［J］.Geometriae Dedicata，1992，41：241-250.

［5］Keith Ball.Volumes of sections of cubes and related problems［J］.Geometric Aspects of Functional Analysis，1989，13 76:251-260.

［6］John F.Extremum problems with inequalities assubsidiary conditions［M］.Courant Anniversary Volume.New York:Interscie nce，1948：187-204.

［7］英起志.凸体体积比的相关性质［J］.上海大学学报自然科学版，2008，14（4）：373-376.

A formula was given to calculate the volume ratios of n-parallelotope，the asymptotic property of the volume ratios was observed，and some values of volume ratios of n-parallelotope were calculated.

n-parallelotope；hypercube；John ellipsoid；volume ratio；asymptotic property

O186.5

A

2096-000X（2016）22-0253-02

英起志（1983-），男，江苏连云港人，江苏商贸职业学院，数学教研室主任，讲师，硕士，研究方向为高职数学教学、凸体几何。