关于正项级数收敛性判别法的几点说明
邓小宇
(贵州财经大学,贵州贵阳550025)
关于正项级数收敛性判别法的几点说明
邓小宇
(贵州财经大学,贵州贵阳550025)
由于正项级数收敛性的判断方法较多,学生掌握起来比较困难。因此,文章就正项级数收敛性判别的几种方法作几点简要的说明,帮助学生解决在做题过程中存在的一些问题。
正项级数;比较判别法;比较判别法的极限形式;比值判别法
正项级数收敛性判别法是高等数学中无穷级数的一个重点和难点。但是,由于正项级数收敛性的判断方法较多,判断正项级数收敛时,学生总是难以选择合适的方法进行判断。因此,文章就正项级数常用的几种收敛性判断方法,做几点说明。
一、正项级数的比较判别法
选择正项级数判别法时,应满足以下条件:
1.正项级数的通项应该容易放大或容易缩小。
2.放大或缩小后的通项构成的正项级数应当是常见的调和级数、等比级数或P-级数,或者该级数的收敛性是比较容易判断的。
3.放大后的通项构成的正项级数必须为收敛的正项级数,缩小后的通项构成的正项级数必须为发散的级数。
二、正项级数的比较判别法的极限形式
1.选作用于比较的已知级数一般为等比级数或P-级数。一般情况下,当正项级数通项中变量n位于幂指函数的指数位置时,选择等比级数与之作比较;当正项级数通项中变量n的位置出现在幂指函数的底数位置时,选择P-级数与之作比较。
2.当正项级数的通项是n→∞时的无穷小量,而其等价无穷小量又容易找到,则可通过等价无穷小量关系找到与之作比较的已知级数。
三、正项级数的比值判别法
一般情况下,当正项级数的通项中含乘积因子n!或an时,可
选择比值判别法。此时,根据比值判别法的判断依据该极限值会比较容易求解。

解:因为通项中含有n!和3n的乘积因子。因此,选择比值判别法,即:
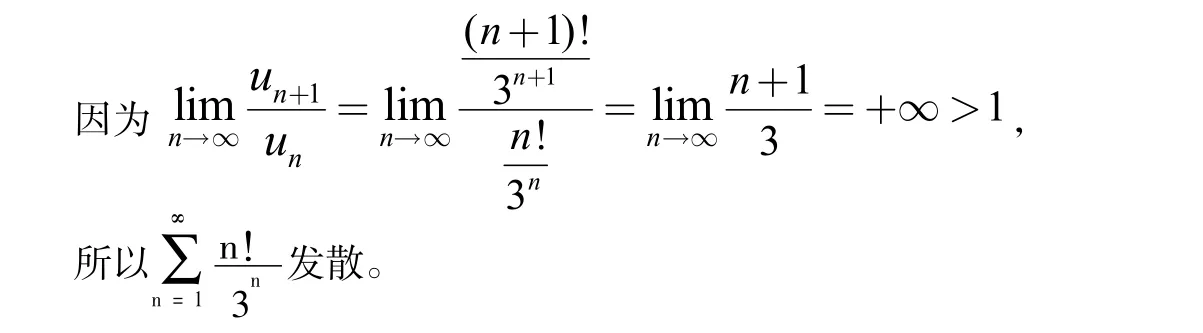
有时对于一个正项级数收敛性的判断,方法可能不止一个。此时,选择比较简单的一种判别法。而有时对于一个正项级数收敛性的判断,往往需要几种判别方法的综合运用。


正项级数收敛性的判断题型灵活多样,在这里我们不能穷尽其所有题型。学生只能是多做题、多思考、多总结,才能掌握好正项级数收敛性的判断方法。
[1]吴传生.经济数学——微积分[M].高等教育出版社,2014.
[2]同济大学数学系.高等数学[M].高等教育出版社,2011.
It is difficult for students to grasp so many convergence of positive series test.Therefore,this paper briefly introduces several methods of positive series of convergence criterion,to help students solve some problems that exist in the study.
series of positive terms;comparative judgment method;the limit form of comparative judgment method;the ratio test
O13
A
2096-000X(2016)22-0263-02
邓小宇(1978,11-),女,贵州毕节市人,贵州财经大学数学与统计学院,副教授,研究方向:数学教育。

