斯特潘—玻尔兹曼定理的简单热力学推导
艾志伟 吴昊
(武汉大学 物理与技术学院,湖北武汉430072)
斯特潘—玻尔兹曼定理的简单热力学推导
艾志伟 吴昊
(武汉大学 物理与技术学院,湖北武汉430072)
斯特潘-玻尔兹曼定理是肤色系统中最为重要的定理之一,描述了辐射系统的能量密度和热力学温度之间的关系。同时,在大学物理之中斯特潘-玻尔兹曼定理也有着相当重要的地位。在文中主要就斯特潘-玻尔兹曼定理的简单热力学推导进行分析,希望以此来对斯特潘-玻尔兹曼定理有着更加深刻的认识。
斯特潘-玻尔兹曼定理;简单热力学;推导
大学物理包括力、热、电、磁、光以及近代物理几个部分组成,是理工农医学生必修重要基础课程。目的培养学生的创新能力和实践能力、提高学生的科学素质打下基础的极其重要的教学环节。作为上课的老师应该把教材上的内容讲解清楚透彻,教材上的内容由于篇幅限制不可能把所有内容都一一俱到。比如近代物理黑体辐射斯特潘-玻尔兹曼定理一般教材上只是给出公式,没有具体的推导过程。少数教材说明了根据热力学理论或统计物理知识可以推导该公式。非物理专业学生很难推导斯特潘-玻尔兹曼定理。文章用三种简单的热力学方法,推导了黑体辐射斯特潘-玻尔兹曼定理,以帮助学生理解。
引言
斯特潘-玻尔兹曼定理(Stefan-Boltzmann's law)描述了一个辐射系统的能量密度与其热力学温度之间的关系,是辐射理论中最初也是最重要的定理之一。这个定理最初是由斯洛文尼亚物理学家约瑟夫·斯特潘(Josef Stefan)在整理法国科学家杜龙(Pierre Louis Dulong)和珀替(Alexis Thérèse Petit)的实验结果后给出的。他的学生玻尔兹曼(Ludwig Boltzmann)将他的结论拓展到灰体辐射,利用辐射场作为热机的工作物质,得到了我们现在称为斯特潘-玻尔兹曼定理的结论。斯特潘利用这条定理,第一次较精确地给出了太阳表面温度为5700K。
现今,这条定理是利用普朗克黑体辐射定理推导出的,但是它的一种表达形式,即辐射场的体能量密度与其热力学温度的四次方成正比这种关系,也可以采用多种比较初等的热力学方法得到。
推导过程中,需要应用:

这个前提条件,其中ρ是辐射场压强,u(T)是辐射场的内能密度。这个关系可以从经典热力学[1],统计力学[2]或者电动力学[3]得到。
一、推导过程
下面我们采用三种简单的热力学方法来推导斯特潘-玻尔兹曼定理,其核心思想都是采用了热力学第二定律。
证明一:
我们以辐射场作为工作物质,构造一个卡诺热机。热机的两个热源,选择两个平衡态辐射源,温度分别是T1,T2,其中T1的温度比较高。卡诺循环是由两个等温过程和两个绝热过程组合起来的循环。在循环的第一步,进行等温膨胀过程,热机从温度T1的辐射场吸热,在辐射压强ρ1下等温膨胀,与辐射场热平衡。
由式(1)可以看出,对热辐射来说,温度T不变,则其内能密度u(T)就不变,所以辐射压强ρ也不变。换句话说,对辐射场而言,相图上的等温线就是等压线。于是当辐射场体积从V1增加到V2时,其对外做功为:
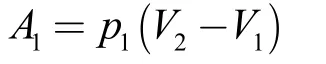
在这个等温过程中,辐射场内能密度不变,但是体积从V1增加到V2,则其总内能增加了:
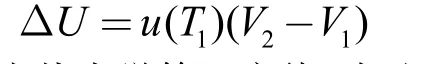
由热力学第一定律,在这个过程中,热机从热源T1吸收的热量是:
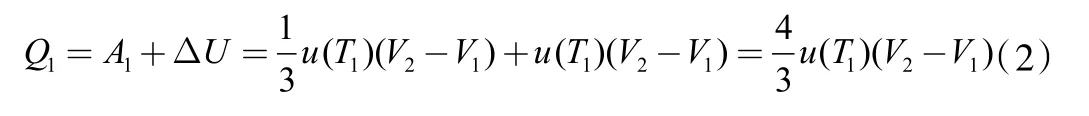
假定这个循环中,热源温度T1和T2只相差一个非常微小的量dT,其体积改变量也是一个小量dV=V2-V1,于是,在这个循环过程中,热机对外做的功,就是这个循环过程所包围的面积,可以近似看作一个平行四边形的面积,即是:
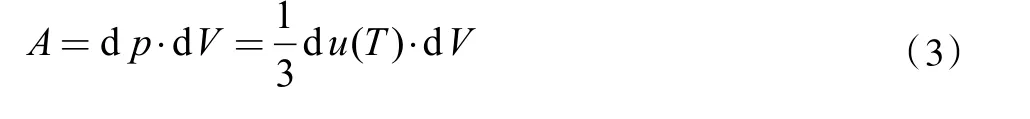
代入式(2)的结果,这个热机的效率是:
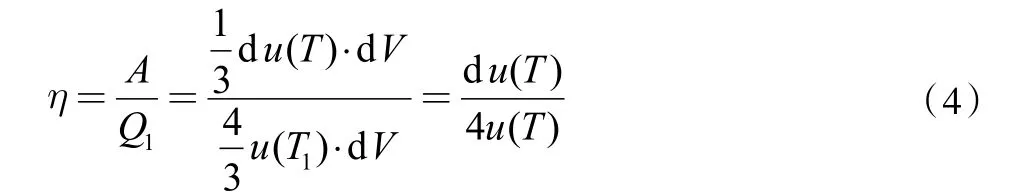
由卡诺定理,我们知道,一个卡诺热机的效率是[1]:

对比式(4)和式(5),可以看到:
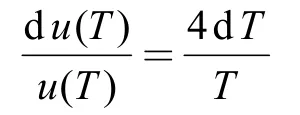
积分后,考虑当热力学温度T=0 K时,辐射场能量密度为零,就有:
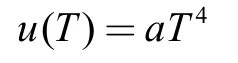
即是,辐射场的体能量密度与其热力学温度的四次方成正比。其中a是积分常数,也称为斯特潘-玻尔兹曼常数。
这个推导过程,应用了卡诺定理。卡诺定理是热力学第二定律的一个重要推论。利用卡诺定理,可以证明许多有用的理论,比如相变理论中重要的克拉伯龙方程。
证明二:
由卡诺定理,我们可以得到一个关系式[4]:

利用这个式子,可以简单的证明斯特潘-玻尔兹曼定理。
一个辐射场的内能,可以表达为单位体积内能,即内能密度乘以其体积,即是:

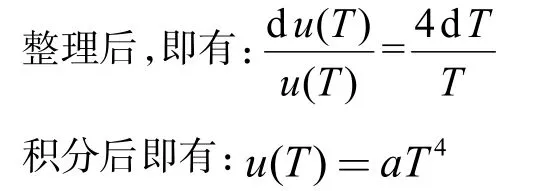
证明三:
上述两种证明方式都应用了卡诺定理,我们知道,卡诺定理是可以从热力学第二定律导出的,所以,应用热力学第二定律,也可以直接给出斯特潘-玻尔兹曼定理。
由热力学第二定律的微分形式:
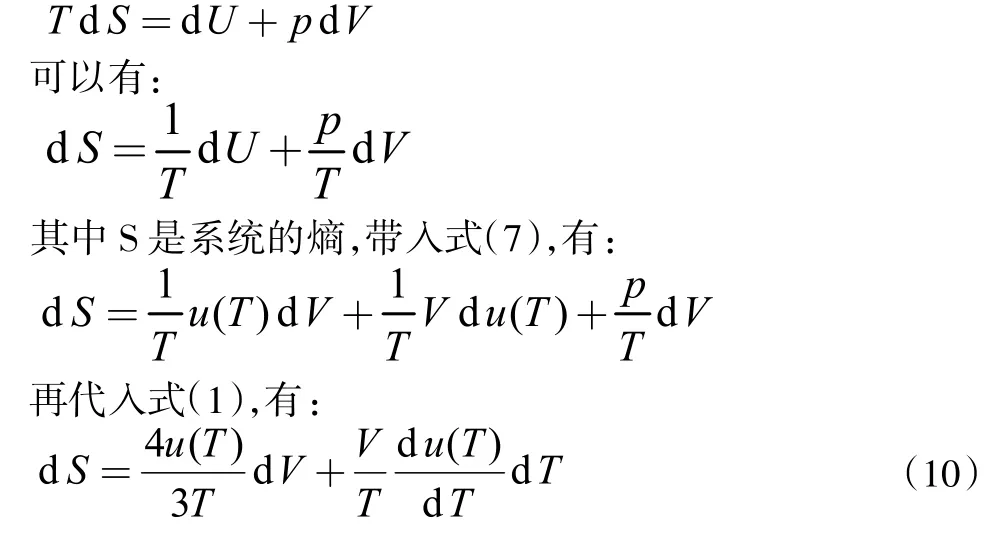
将S看作是T和V的函数,进行全微分,有:

对比式(10)和式(11),有:

将式(12)对T求偏微分,有:
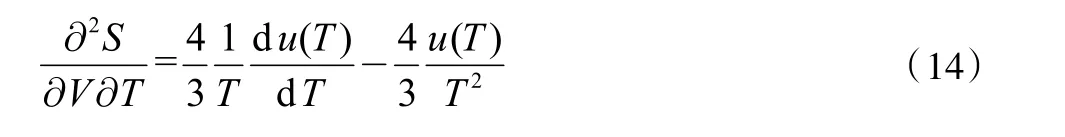
同样的,将式(13)对V求偏微分,有:

对于热力学函数S来说,其二阶偏微分满足:

二、结束语
在文章中,我们用三种不同方式证明了辐射场的能量密度和其热力学温度的四次方成正比。其中斯特潘-玻尔兹曼常数(a=5.67×10-8W·m-2·K-4)在我们的推导中是以一个积分常数形式出现的,不能给出具体数值,而根据普朗克黑体辐射定理,可以给出这个常数具体的数值。需要说明的是,斯特潘-玻尔兹曼定理有很多种证明方式,我们在这儿给出的,是其中最为简单、最容易被学生理解的几种热力学方式。掌握这几种方式推导的过程,可以有助于学生更好的理解如何应用热力学第二定律和卡诺定理去解决一些问题,也能够加深他们对黑体辐射中斯特潘-玻尔兹曼定理的理解和掌握。
[1]杨素琴.平衡辐射场压强的探讨[J].雁北师范学院学报,2004,20(2):11-13.
[2]佟华.空腔辐射中辐射压强与辐射能量密度之间关系[J].吉林师范大学学报(自然科学版),2005(3):123-124.
[3]袁德荣.介质表面辐射压强的研究[J].湖北大学学报(自然科学版),1998,20(1):36-39.
[4]李椿,章立源,钱尚武.热学(第二版)[M].2008.
Stefan-Boltzmann law system is one of the most important theorems in the color system,describes the relationship between the energy density and the thermodynamic temperature radiation system.At the same time,in the university physics Stefan-Boltzmann law also has a very important position.In this paper mainly the simple thermodynamic derivation Stefan-Boltzmann law is analyzed,hoping to more profoundly understand the Stefan-Boltzmann law.
Stefan-Boltzmann law;Simple Thermodynamics;deduction
G642
A
2096-000X(2016)22-0088-02
艾志伟(1966,10-),男,汉族,职称:讲师,学历:博士,研究方向:半导体器件方面研究工作。

