共射-共集反馈放大器高频响应仿真与分析

赵鑫，王江涛，杨一军，陈得宝，李峥，方振国，李素文

（淮北师范大学物理与电子信息学院，安徽淮北235000）

共射-共集反馈放大器高频响应仿真与分析

赵鑫，王江涛，杨一军，陈得宝，李峥，方振国，李素文

（淮北师范大学物理与电子信息学院，安徽淮北235000）

对共射-共集电压并联负反馈放大电路采用方框图法计算基本放大器和反馈放大器的源互阻增益，结果的正确性经高频小信号等效电路在EWB软件下的仿真和MATLAB结点电压法下的数值解得以验证.软件分析显示，开、闭环的上限频率之比是反馈放大器的源反馈深度，满足单极点开、闭环上限频率间关系，说明电路中有上限频率远小于其它的主极点.采用开路时间常数法讨论下各结电容对上限频率的影响，得到无论开、闭环状态，容量较小的共射电路集电结电容都因回路电阻大，造成极点上限频率低，在频率响应中起主要作用的结论.以上分析方法可用于讨论多极点系统中的各极点频率，以便针对性调整电路参数，改善系统频率特性.

共射-共集；上限频率；MATLAB；EWB

0 引言

共发射极放大电路放大能力强，共集电极电路有很强的带负载能力，组合后的电路兼有两种电路的优点，引入电压负反馈后可以使输出电压更加稳定，带负载能力进一步提高.上限频率是放大器重要参数之一，拓展频带宽度可以采用多种方法，采用组合电路是常用的手段之一，引入负反馈则可提高上限频率.目前组合电路和单管复合类型的频率响应，以及探讨反馈放大器性能方面都屡见报道［1-5］，但关于反馈放大器频率响应方面的迄今尚未见到.本文借助仿真软件，构建了共射-共集（common emitter and common collector）电压并联负反馈放大电路，理论上计算了多级放大器的静态电流、交流参数、开闭环源增益.有开、闭环的源增益与软件仿真结果相一致，且开闭环增益满足反馈放大器中的基本关系.经分析各结电容极点对上限频率的影响，得到共射组态中集电结电容回路电阻高，时间常数大，由其极点确定的上限频率远小于其它，是电路的主极点的结论.在该结论下，闭环上限频率扩展的倍数就是增益下降的倍数，满足增益带宽积不变.上述分析方法为讨论多极点反馈放大器的频率响应提供一种有效途径.

1 组合放大电路和高频等效电路

共射-共集组合放大电路如图1所示，电键位于P为反馈放大器，位于Q则为考虑反馈网络负载效应的基本放大器.T1、T2管基极电流IB1、IB2可分别用下式表示其中VBB=RB2VCC/（RB1+RB2），RB=RB1//RB2，VBE（on）=0.7 V.取β1=β2=β=50，将图1电路中各电阻值代入式（1）和式（2），计算可得IB1=18.481 μA，IB2=19.601 μA.输出端加载示波器启动仿真，无失真现象，表明动态范围在放大区.

图1 共射-共集组合放大电路

与图1相对应的简化高频小信号等效电路如图2所示.由rb′e=26 mV/IB和gm=β/rb′e计算有：rb′e1= 1.406 8 kΩ；rb′e2=1.326 5 kΩ；gm1=35.541 mS；gm2=37.694 mS.图2中rbb′1、rbb′2是基区体电阻，小功率管多在几十到几百欧［3］（此处取rbb′1=rbb′2=100 Ω）.Cb′c是集电结反偏时的势垒电容，多在2～10 pF［7］（不失一般性，取5 pF）；Cb′e是发射结电容，与晶体管特征频率fT关系为

小功率管的特征频率典型值在100～1 000 MHz之间［7］（此处取200 MHz），由式（3）得Cb′e1=23.283 pF，Cb′e2= 24.996 pF.

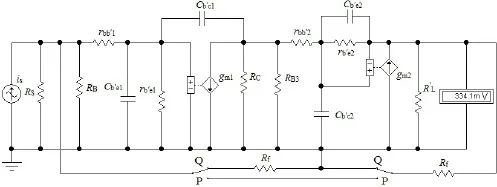
图2 共射-共集简化高频等效电路

2 源互阻增益

在电压并联负反馈情况下，增益内涵为互阻增益.中频下的极间电容视为开路，根据图2，中频开环互阻增益Arsm可表示为

其中

分别是第一和第二级放大电路的中频电压增益，而R′L=RE3//Rf//RL，代入数据可得Arsm=-334.21 kΩ.利用闭开环增益间普遍成立的基本关系，可得中频源闭环互阻增益Arfsm

其中kfg是互导反馈系数，有kfg=-1/Rf；Fs是源反馈深度，有Fs=1+kfgArsm.代入数据有Arfsm=-101.13 kΩ，Fs= 3.304 9.

3 仿真分析

3.1 EWB仿真

对图1基本电路、图2等效电路分别切换电键于M、N位置，启动仿真，读出输出电压vo，比电流源is，可得闭、开环下的源增益，具体见表1.可以看到仿真结果和理论计算一致性很好，说明电路设计合理，各管都工作于线性度很好的线性区.采用文献［1］方法，启动交流仿真，切换电键可分别得开、闭环的上限频率fH和fHf，具体见表1.

表1 开闭环增益、上限频率一览

3.2 MATLAB分析

对图2等效电路利用MATLAB编程，可求各结点电压，输出结点电压对电流源的比值，即为Arsm.在s域中列写结点方程编程运行后有如下结果.

（1）中频开、闭环源互阻增益.在f=1 kHz时，开环下得vo=v5=-334.21 mV，即Arsm=-334.21 kΩ，较式（4）计算略小，这是取f=1 kHz所致.修改参数知，频率越低，相差越小，当f=0转为直流后，电容完全断开，两者没有任何差别.将式（8）、（12）分别增加一项-v5/Rf和-v1/Rf，这时对应为闭环s域结点方程.运行程序后Arfsm=-101.126 kΩ，与利用反馈放大器基本关系式（7）所计算结果相同.

（2）幅频特性.使用for循环语句，取f步长为100 Hz，分别做出|Ars|和|Arfs|对f关系曲线，结果如图3所示.可以看到，|Ars|和|Arfs|都随频率增大减小，且|Ars|较|Arfs|减小更快些.

图3 MATLAB环境下幅频特性

（3）上限频率.分别采用if语句，增加频率，使得|Ars|、|Arfs|不断减小，当其下降到|Arsm|或|Arfs|的0.707倍时，结束循环，显示当前频率.运行有fH=85.8 kHz、fHF=284 kHz.

4 讨论

（1）组态对上限频率影响.令T1管结电容为0，仅共集电极组态结电容影响频率特性，运行程序可以得到共集组态开闭环上限频率，具体见表2.同理可得共发射极组态上限频率.由表2知，共集电路上限频率远大于共射，电路的频率特性表现为单极点.由图2不难得知，频率升高，容抗减小，使得vb′e2减小，致使g′m2vb′e2减小，造成Ars下降，但容抗减小的同时又会使得T2管基极电流增大，缓减了Ars的下降，且没有密勒倍增效应［3］，故上限频率远较共射大.

表2 不同组态上限频率一览

代入fH可以求得283.56 kHz，与列写闭环结点方程的MATLAB分析结果284 kH吻合很好，说明满足单极点近似条件.同样，将表2中共射和共集组态的fHf对fH做比，与Fs=3.304 9的结果很接近，说明增益带宽积保持不变ArsmfH=ArfsfHf.

（3）上限频率的近似估算.在极点数为N的多极点系统中，上限频率fH可近似表示为

（2）开、闭环上限频率.开闭环上限频率在单极点条件下为

其中fHk是第k级的上限频率.当某级的上限频率较其它小于4倍，则该极点为主极点，电路的上限近似为该级的上限频率.在求任意一个结电容C对应的时间常数τ时，应将其它电容理想化，做开路处理（开路时间常数法），然后求该电容所在回路的等效电阻R，则时间常数τ=CR，上限频率f=1/（2πτ）［8］.根据电路理论，此上限频率就是该电容对应的极点频率.

R的求法很多，解析表达式可以通过断开C，分析断开处各电阻间关系得到；数值解可以编写结点方程，做C断开处电压与流入电流的比获得，也可以用EWB直接仿真.本文在EWB环境下，断开电容，在断开处加VS=10 V直流电压源，同时串入直流电流表，测得流入电流Is，R=VS/Is即为等效电阻.将各级的结电容进一步细化，按上述过程得到的各结电容极点上限频率，如表3所示.

表3 各极点对应的等效电阻、上限频率

由表3可以看到，无论开闭环状态，Cb′c1极点对应的上限频率远小于其它，原因是它的回路电阻R很大，使得τ很大，超过其它结电容的4倍，成为电路的主极点，近似认为它的上限频率就是整个电路的上限频率.开、闭环上限频率的计算表明，式（14）与直接采用主极点表示的相对误差都是0.41%，属非常好的近似.另外，无论是组合或其它组态电路，它们的主极点开、闭环上限频率都满足反馈放大器频率响应的基本关系.

5 结束语

在得到组合电路开、闭环互阻增益满足反馈放大器基本关系的基础上，对反馈放大器频率响应进行了探讨.结果表明：无论开闭环，都有T1集电结电容所在回路电阻很大，造成时间常数远大于发射结，构成主极点，对上限频率起主要作用，满足闭环上限频率较开环扩展Fs倍关系.上述开路时间常数法适用于分析上限频率，不难推广，在分析下限频率时则采用短路时间常数法，可为分析各种多极点系统的频率响应提供一种有效方法.

［1］杨一军，王江涛，陈得宝，等.基于MATLAB的共基-共集高频响应仿真与分析［J］.安徽理工大学学报（自然科学版），2015，35（3）：21-25.

［2］赵鑫，邹峰，陈得宝，等.共基复合管放大电路高频响应的分析和仿真［J］.淮北师范大学学报（自然科学版），2015，36（3）：26-29.

［3］杨一军，陈得宝，方振国.差分-共基负反馈放大器的理论计算与微变等效电路仿真［J］.淮北师范大学学报（自然科学版），2013，34（4）30-33.

［4］杨一军，陈得宝，王江涛，等.基于POS的负反馈电路参数自适应优化及仿真分析［J］.计算机工程与科学，2014，36（7）：1404-1408.

［5］杨一军，陈得宝，方振国，等.基于微变等效电路的差分—共基负反馈放大器的仿真与分析［J］.北京电子科技学院学报，2014，22（6）：74-76.

［6］谢嘉奎，宣月清，冯军.电子线路（线性部分）［M］.4版.高等教育出版社，1999：228.

［7］康华光，陈大钦.电子技术基础（模拟部分）［M］.4版.高等教育出版社，1999：121，124.

［8］童诗白，华成英.模拟电子技术基础［M］.4版.高等教育出版社，2006：244.

The Simulation and Analysis of High Frequency Response of Common Base-Common Emitter Feedback Amplifier

ZHAO Xin，WANG Jiangtao，YANG Yijun，CHEN Debao，LI Zheng，FANG Zhenguo，LI Suwen
（School of Physics and Electronic Information，Huaibei Normal University，235000，Huaibei，Anhui，China）

The theoretical calculation of source transimpedance gain between basic amplifier and feedback amplifier of the common base-common emitter parallel voltage negative feedback amplifier circuit is carried out by the diagram method.The correctness of the results is validated by the numerical solution of the high frequency small-signal equivalent circuit using EWB and MATLAB respectively.Software analysis indicates that the ratio between open and close loop cut-off frequency gives the feedback depth of feedback amplifier，and it meets with the conditions of single pole.This illustrates that there exists upper limit frequency which is smaller than other main pole far away.The time constant open circuit method is used to analyze the junc⁃tion capacitance′s effect on upper limit frequency.And we get the conclusion that despite open loop or close loop state，common emitter junction capacitance with small capacity plays a main role in frequency response，for it has large loop resistance.Above mentioned method can be applied to analyze poles frequency in multi⁃ple pole system，so as to make corresponding adjustment on circuit parameters and enhance the frequency property of the system.

CE-CC；upper limit frequency；MATLAB；EWB

TN 721

A

2095-0691（2016）03-0038-05

2016-03-21

安徽省高等学校自然科学研究一般项目（KJ2016B005）；安徽省教育厅质量工程项目（2012gxk057）；重大教改项目（2014zdjy060）；名师工作室（2015msgzs138）；一般教研项目（2014jyxm166，2015jyxm163）；淮北师范大学重点教研项目（Jy14120）；淮北师范大学一般教研项目（Jy15126）

赵鑫（1980-），女，安徽萧县人，讲师，研究方向：电子信息处理；通讯作者：杨一军（1956-），男，教授，浙江宁波人，研究方向：电子技术.