酉求根MUSIC算法在双基地MIMO雷达中的应用
刁鸣, 李永潮,高洪元
(哈尔滨工程大学 信息与通信工程学院,黑龙江 哈尔滨 150001)
酉求根MUSIC算法在双基地MIMO雷达中的应用
刁鸣, 李永潮,高洪元
(哈尔滨工程大学 信息与通信工程学院,黑龙江 哈尔滨 150001)
研究双基地多输入多输出(MIMO)雷达多目标波离角(DOD)和波达角(DOA)的联合估计问题,提出一种酉求根多重信号分类(MUSIC)算法。该算法在求根MUSIC算法基础上,利用协方差矩阵的中心Hermite对称性质,通过酉变换将协方差矩阵的复数运算转为实数,进行实值特征分解得到噪声子空间,对比原协方差矩阵和实值协方差矩阵的特征对应关系,得出酉求根MUSIC谱函数,分两步分别估计目标DOA和DOD,且计算结果自动配对。相对于传统求根MUSIC算法,该算法只进行协方差矩阵的实值特征分解而不需要进行复数运算,因此大大降低了计算量,而且在不降低阵列孔径的条件下无需空间平滑即具有解相干能力。计算机仿真证明了该算法的有效性。
多输入多输出雷达;波离角;波达角;酉求根MUSIC算法;实值协方差矩阵
多输入多输出(multiple-input multiple-output, MIMO)雷达是由国外学者将通信领域的MIMO思想引入雷达领域所提出的一种新体制雷达[1]。 MIMO雷达通过多个发射阵元同时发射相互正交的波形,且利用多个接收阵元同时接收目标的回波信号,具有可利用波形分级和空间分级增益,以及更高的自由度等优点,因而受到了广泛的关注。有关MIMO雷达的波离角(DOD)和波达角(DOA)估计的研究是研究热点之一,相关研究主要围绕经典测向算法展开[2-10]。文献[2-6]研究了基于ESPRIT的相关算法,文献[2-4]基于双基地MIMO雷达,分别提出了EPSRIT算法[2]、共轭EPSRIT算法[3]和酉ESPRIT算法[4],算法的效率和性能都得到一定的提升,但只有酉ESPRIT算法具有解相干能力,其他算法的性能在存在相干信源时急剧恶化。文献[5-6]基于单基地MIMO雷达分别提出了采用非圆信号的ESPRIT算法和降维酉EPSRIT算法。文献[7]利用最大似然的方法估计MIMO雷达的波达方向,该方法虽然可以用于相干信源的角度估计,但计算量非常大。文献[8-10]则研究了MUSIC算法在双基地MIMO雷达中的应用,文献[8]将二维谱峰搜索MUSIC算法转换为只需一维搜索的降维MUSIC算法,分别估计出DOA和DOD,计算量显著降低,但不具备解相干能力;文献[9]提出了基于MIMO雷达的求根MUSIC方法,通过将传统求根MUSIC算法应用于MIMO雷达,分两步分别估计出DOD和DOA,避免了计算量巨大的谱峰搜索,其计算量相对于文献[8]的方法有所降低,但计算效率仍有待提升,且当目标相关或相干时性能严重恶化,算法失效。考虑到实际噪声环境的复杂性,文献[10]研究了基于双基地MIMO雷达的四阶累积量,提出了可以用于色噪声环境下的估计方法,该方法需要二维谱峰搜索,计算量巨大,且只能估计相互独立的信源。
针对双基地MIMO雷达中现有角度估计算法计算量大及无法估计相干信源的问题,提出一种酉求根MUSIC方法。该方法将信号协方差矩阵进行实值化处理,将复运算转换为实运算,构造实值求根方程,分两步分别估计DOA和DOD,结果自动配对。
1 双基地MIMO雷达数据模型
图1所示为双基地MIMO雷达模型。
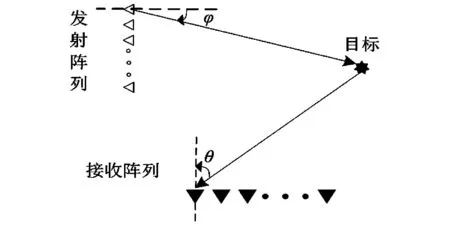
图1 双基地MIMO雷达示意图Fig.1 Structure of bistatic MIMO radar
考虑如图1所示双基地MIMO雷达,发射阵列和接收阵列分置,均为阵元间距为半波长的均匀线阵,分别由M个和N个全向的阵元组成。M个发射阵元同时发射M种具有相同载频和带宽的正交波形,接收端通过匹配滤波器将M种波形分开。 假设在同一距离存在P个相互独立的远场信源,第t个快拍接收端全部匹配滤波器的输出信号为

(1)
式中:A=[a1a2… aP] 为MN×P维的目标导向矢量矩阵,ar(θp)=[1 e-jπsin θp… e-j(N-1)πsin θp]T为接收导向矢量,at(φp)=[1 e-jπsin φp… e-j(M-1)πsin φp]T为发射导向矢量,ap=ar(θp)⊗at(φp)为第p个目标的导向矢量,⊗表示Kronecker积,θp表示第p个目标的波达方向,即DOA,φp表示第p个目标的波离方向,即DOD;s(t)=[s1(t)s2(t) …sP(t)]T表示为P×1维信号反射复幅度向量,sp(t)=βpej2πfdt,βp表示幅度,fd表示多普勒频移;n(t)表示MN×1维的复高斯白噪声向量,其均值为零,协方差矩阵为σ2IMN,其中σ2表示噪声功率,IMN表示MN×MN维的单位矩阵。
由L个快拍构成的数据矩阵为

(2)
式中:X=[x(1)x(2) …x(L)]表示MN×L维接收快拍矩阵,S=[s(1) s(2) … s(L)]为P×L维回波矩阵,N=[n(1) n(2) … n(L)]为MN×L维噪声矩阵。
2 实值协方差矩阵的构造
由L个快拍的数据矩阵X计算协方差矩阵的最大似然估计可得
(3)
式中:R5=E[s(t)sH(t)]=SSH为回波矩阵的协方差矩阵。只有当R5为对角矩阵时,R才具有中心Hermite对称性质[12],即
(4)
式中:JMN表示MN×MN维的交换矩阵,其副对角线位置上的元素均为1,其他位置上的元素均为0;(·)*表示复共轭;JMN满足JMN2=IMN。当Rs不是对角矩阵时,常使用R的前后向平均形式RFB[4,11,12],用来增强其中心Hermite对称性质和增加虚拟快拍数,RFB可表示为
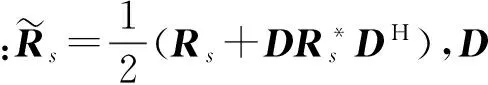
D=diag(exp[j(N-1)πsinθ1+j(M-1)πsinφi],
(6)
且D满足
(7)
由于任意的中心Hermite对称矩阵经过酉变换均可以得到实值矩阵[12]。因此对中心Hermite对称矩阵RFB进行实值变换,可以获得实值协方差矩阵:
(8)
式中:QMN为一稀疏的酉转换矩阵,满足如下性质:
(9)
(10)
根据以上性质可以将QMN根据MN的奇偶不同选取如下不同形式[12]:
(11)
(12)
考虑式(5),RU可进一步改写为
(13)
对比式(8)和式(13)发现,RU有两种构成方式,一种可以直接使用协方差矩阵R进行酉转换,然后取其实部,另一种为使用协方差矩阵的前后向平均形式RFB进行酉变换获得,二者均可用于实值协方差矩阵的构造。
3 酉求根MUSIC算法
对协方差矩阵的前后向平均RFB和实值协方差矩阵RU进行特征分解可得:
(14)
(15)
式中:EFB和VFB分别代表RFB的信号子空间和噪声子空间,EU和VU分别代表RU的信号子空间和噪声子空间,EFB和EU为MN×P维矩阵,VFB和VU为MN×(MB-P)维矩阵,ΣS和ΠS分别为由RFB和RU的P个大特征值构成的特征值矩阵。
下面通过分析RFB和RU的特征方程来获得二者的信号子空间和噪声子空间之间的关系。RFB的特征方程可表示为
(16)
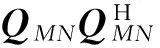
观察式(17)可知,RFB和RU具有相同的特征值,且其对应特征向量,即特征子空间之间的关系可表示为
(18)
(19)
由传统root-MUSIC的原理可以求得双基地MIMO雷达的求根多项式:
(20)

基于式(20)所示求根多项式以及式(18)、(19)所示的关系式,双基地MIMO雷达的酉求根(URM)多项式可表示为
(21)
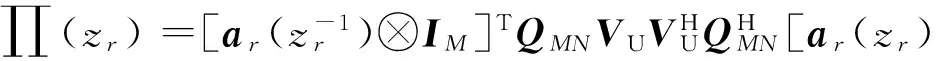
(22)
所得的所有根中,P对离单位圆最近的根zr(p)|p=1,…,p即为对应的DOA,实际计算时不妨取位于单位圆内的离单位圆最近的P个解作为DOA的估计值。
将由式(22)求得的每个zr(p)分别代入式中,可得对应DOD的求根多项式:
(23)
再次利用信号子空间和噪声子空间的正交关系,令
(24)
所得的根中离单位圆最近的一对根zt(p)即为与相应DOA对应的DOD。不妨与DOA的选取类似,取位于单位圆内的根作为DOD的估计值。
DOA和DOD与zr(p)和zt(p)的转换关系式为
(25)
(26)
由式(25)、(26),可估计出第p个目标的DOA和DOD,且无需额外的配对算法即可进行自动配对。
4 仿真实验和结果分析
为了证明所提方法的有效性和优越性,分别在不同场景下进行了系统的计算机仿真实验。
定义均方误差公式为
(27)
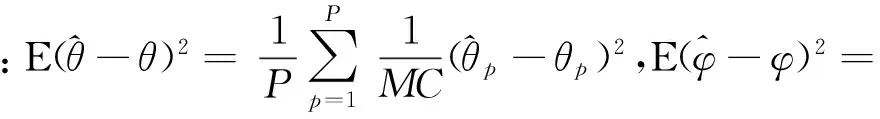
考虑一双基地MIMO雷达,其结构如图1所示,发射阵元数M=8,接收阵元数N=6。假设在同一距离单元内存在P=3个远场点目标,其收发角分别为(φ1,θ1)=(5°,-10°),(φ2,θ2)=(27°,8°),(φ3,θ3)=(13°,25°),快拍数为L=100。
实验13个目标相互独立时,分别在信噪比SNR=10 dB和SNR=0 dB的情况下进行100次蒙特卡罗仿真,图2(a)、(b)分别给出了所提算法的三个目标在SNR=10 dB、SNR=0 dB时的角度估计计算结果。可以看出,所提算法的角度估计结果正确,且在信噪比较低的情况下仍能有效配对。
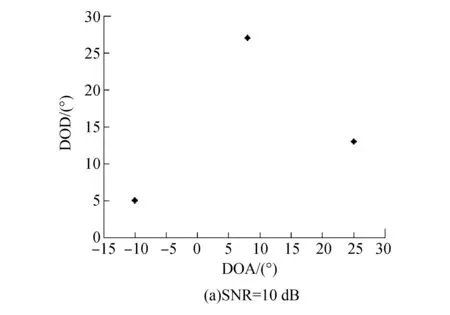

图2 文中所提URM算法在不同SNR下的角度估计Fig.2 Angel estimation of the URM algorithm proposed in the paper versus SNR
实验23个目标相互独立,信噪比SNR由-5 dB变化至30 dB,间隔为5 dB。图3给出了所提算法与文献[9]中所提出的PRF算法、文献[4]中的酉ESPRIT算法和文献[2]中的ESPRIT算法的RMSE随信噪比的变化趋势。可见,所提算法的偏差更小,更稳定,在信噪比较低的情况下优势明显。
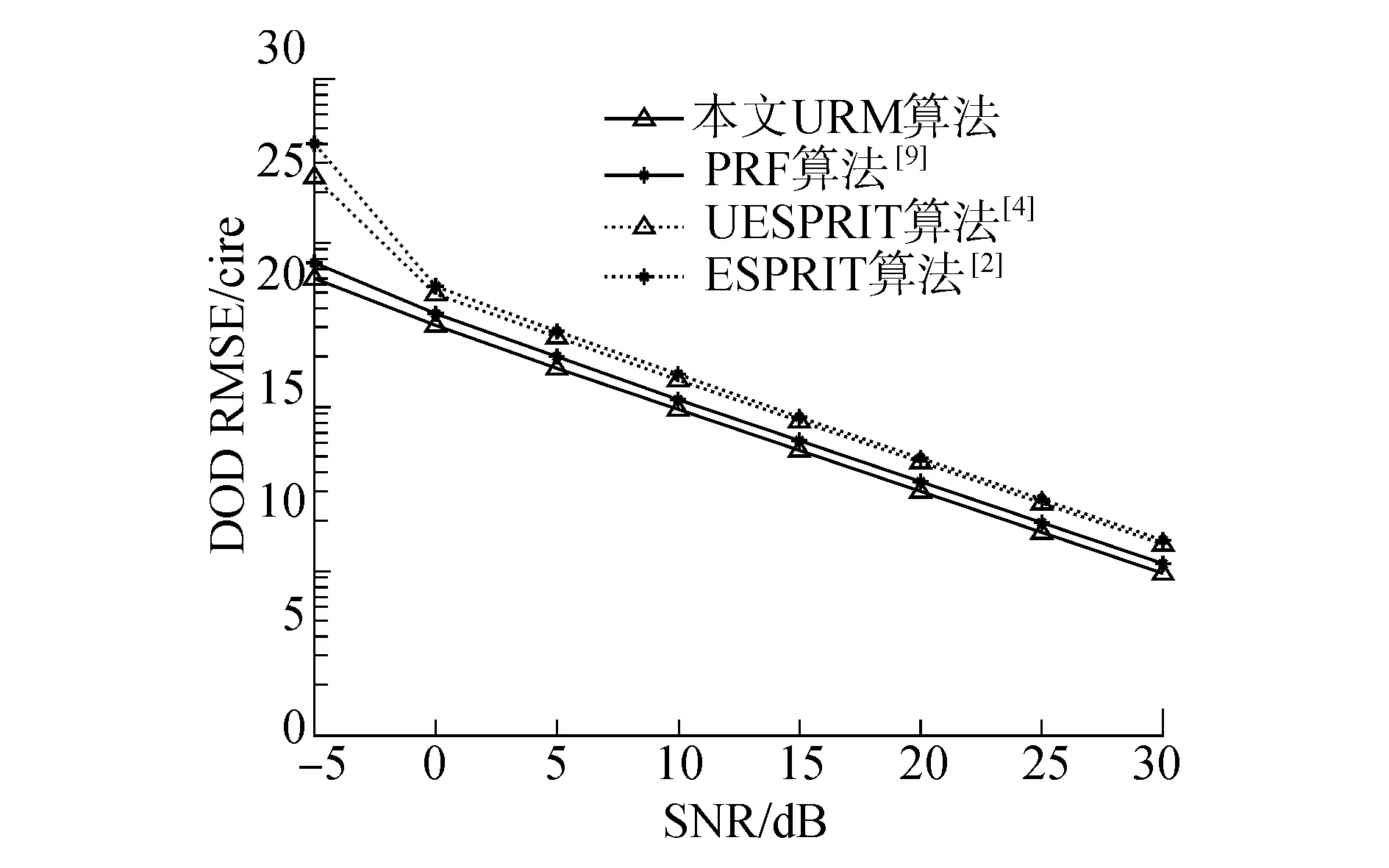
图3 基于独立信源的均方误差随信噪比的变化Fig.3 The RMSE for independent sources versus SNR
实验3第2个和第3个目标相干时,进行100次蒙特卡罗仿真。图4分别给出了所提算法与PRF算法[9]、酉ESPRIT算法[4]的角度估计结果。可以看出,所提算法仍能成功估计和配对,其解相干能力得到证实,而文献[9]中的方法配对失效,文献[4]中方法虽具一定的解相干能力,但性能较差。



图4 基于相干信源的不同算法估计结果Fig.4 Angel estimations in different algorithms based on independent sources
实验4本次实验系统的对比分析了所提算法和文献[4]中算法的解相干能力。本实验中假设存在P=5个远场点目标,分别位于(φ1,θ1)=(-25°,-27°),(φ2,θ2)=(23°,-13°),(φ3,θ3)=(-6°,5°),(φ4,θ4)=(33°,21°)和(φ5,θ5)=(-14°,35°),其中第1个和第2个目标相干,第4个和第5个目标相干。图5给出了所提算法与文献[4]中的酉ESPRIT算法的RMSE随信噪比的变化趋势。可以看出,所提算法的性能优于文献[4]中的酉ESPRIT算法,结果与实验3中的结果吻合。

图5 相干信源的均方误差随信噪比的变化Fig.5 The RMSE for coherent sources versus SNR
实验5文中所提URM方法由于采用了酉变换,将协方差矩阵转化为实值矩阵,较之复数矩阵大大降低了运算量,因此其复杂度比文献[4,9]中的方法都较低。1次复数乘积相当于4次实数乘积,而酉变换将复数运算转换为实数运算,因此大大缩短运算时间。在计算机仿真中,记录下文中所提URM算法和文献[4、9]在相同条件下的计算运行时间进行对比,如图6所示。

图6 相同条件下几种算法运行时间结果Fig.6 Running time in the same conditions
5 结论
1)提出了一种基于双基地MIMO雷达的酉求根MUSIC算法,根据中心Hermite对称矩阵的性质,采用酉变换将协方差矩阵变换为实值矩阵,对实值协方差矩阵进行分解得到噪声子空间,因此降低了计算量。
2)文中所采用的实值处理与空间平滑具有相似效果,但不会降低阵列孔径,算法的解相干能力得到提升。
3)对所提算法和以往算法进行了复杂度分析和实验仿真分析,结果表明,该方法不仅在信号相互独立时估计性能优于现有算法,而且具有良好的解相干能力,符合测向的实际要求。
[1]FISHLER E, HAIMOVICH A, BLUM R S, et al. MIMO radar: an idea whose time has come[C]//Proceedings of the IEEE Radar Conference. Philadelphia, PA, USA: IEEE, 2004: 71-78.
[2]CHEN Duofang, CHEN Baixiao, QIN Guodong. Angle estimation using ESPRIT in MIMO radar[J]. Electronics letters, 2008, 44(12): 770-771.
[3]YANG M L, CHEN B X, YANG X Y. Conjugate esprit algorithm for bistatic MIMO radar[J]. Electronics letters, 2010, 46(25): 1692-1694.
[4]ZHENG Guimei, CHEN Baixiao, YANG Minglei. Unitary ESPRIT algorithm for bistatic MIMO radar[J]. Electronics letters, 2012, 48(3): 179-181.
[5]胡彤, 张弓, 李建峰, 等. 非圆实信号MIMO雷达中基于实值ESPRIT的角度估计[J]. 航空学报, 2013, 34(8): 1953-1959.
HU Tong, ZHANG Gong, LI Jianfeng, et al. Angle estimation in MIMO radar with non-circular signals based on real-valued ESPRIT[J]. Acta aeronautica et astronautica sinica, 2013, 34(8): 1953-1959.
[6]文才, 王彤. 单基地MIMO雷达降维酉ESPRIT算法[J]. 系统工程与电子技术, 2014, 36(6): 1062-1067.
WEN Cai, WANG Tong. Reduced-dimensional unitary ESPRIT algorithm for monostatic MIMO radar[J]. Systems engineering and electronics, 2014, 36(6): 1062-1067.
[7]张娟, 张林让, 刘楠. MIMO雷达最大似然波达方向估计方法[J]. 系统工程与电子技术, 2009, 31(6): 1292-1294.
ZHANG Juan, ZHANG Linrang, LIU Nan. Maximum likelihood DOA estimation of MIMO radar[J]. Systems engineering and electronics, 2009, 31(6): 1292-1294.
[8]ZHANG Xiaofei, XU Lingyun, XU Lei, et al. Direction of departure (DOD) and direction of arrival (DOA) estimation in MIMO radar with reduced-dimension MUSIC[J]. IEEE communications letters, 2010, 14(12): 1161-1163.
[9]BENCHEIKH M L, WANG Yide, HE Hongyang. Polynomial root finding technique for joint DOA DOD estimation in bistatic MIMO radar[J]. Signal processing, 2010, 90(9): 2723-2730.
[10]徐定杰, 李沫璇, 王咸鹏, 等. 色噪声环境下双基地MIMO雷达收发角度估计[J]. 哈尔滨工程大学学报, 2013, 34(5): 623-627.
XU Dingjie, LI Moxuan, WANG Xianpeng, et al. Joint DOD and DOA estimation for bistatic MIMO radar in colored noise[J]. Journal of Harbin engineering university, 2013, 34(5): 623-627.
[11]PESAVENTO M, GERSHMAN A B, HAARDT M. Unitary root-MUSIC with a real-valued eigendecomposition a theoretical and experimental performance study[J]. IEEE transactions on signal processing, 2000, 48(5): 1306-1314.
[12]HAARDT M, NOSSEK J A. Unitary ESPRIT: how to obtain increased estimation accuracy with a reduced computational burden[J]. IEEE transactions on signal processing, 1995, 43(5): 1232-1242.
本文引用格式:
刁鸣, 李永潮,高洪元. 酉求根MUSIC算法在双基地MIMO雷达中的应用[J]. 哈尔滨工程大学学报, 2016, 37(9): 1292-1296.
DIAO Ming,LI Yongchao,GAO Hongyuan. Unitary root-MUSIC algorithm for bistatic MIMO radar[J]. Journal of Harbin Engineering University, 2016, 37(9): 1292-1296.
Unitary root-MUSIC algorithm for bistatic MIMO radar
DIAO Ming,LI Yongchao,GAO Hongyuan
(College of Information and Communication Engineering,Harbin Engineering University,Harbin 150001,China)
In this paper, we investigate the estimated joint direction of departure (DOD) and direction of arrival (DOA) for bistatic multiple-input multiple-output (MIMO) radar, and propose a unitary root-MUSIC algorithm. Based on the traditional root-MUSIC algorithm, the proposed algorithm uses the centro-Hermitian property of a covariance matrix to transform complex operations into real numbers in a covariance matrix by unitary transformation. We conduct a real-valued eigen decomposition to obtain the noise subspace. We then analyzed the inner relationship between the original covariance matrix and the real-valued covariance matrix to obtain the unitary root-MUSIC polynomial. We estimated the DOA and DOD in two steps with an automatic pairing. Compared with the conventional root-MUSIC, the proposed algorithm greatly reduces computational complexity in the eigen analysis stage of the root-MUSIC because it exploits the eigen decomposition of a real-valued covariance matrix. It can also address decoherence without using space smoothing, in the condition of not debasing the array aperture. Our simulation results verify the effectiveness of the proposed algorithm.
MIMO radar; DOD; DOA; unitary root-MUSIC algorithm; real-valued covariance matrix
2015-10-27.
时间:2016-09-07.
国家自然科学基金项目(61571149).
刁鸣(1960-), 男, 教授, 博士生导师.
刁鸣,E-mail: diaoming@hrbeu.edu.cn.
10.11990/jheu.201510065
TN911.7
A
1006-7043(2016)09-1292-05
网络出版地址:http://www.cnki.net/kcms/detail/23.1390.u.20160907.1042.002.html

