杭长客专轨道控制网区段搭接方式探讨

柳培清

(中铁第四勘测设计院集团有限公司，湖北 武汉 430079)



杭长客专轨道控制网区段搭接方式探讨

柳培清

(中铁第四勘测设计院集团有限公司，湖北 武汉 430079)

高铁建设因为要求精度高、施工时间长、投入大，往往一条线路分为几个甚至几十个标段进行施工，轨道控制网的测设不可能一次性完成，只有施工进行一部分，测设一部分，合理的区段搭接方式是保证高速铁路平稳运行的基础。本文通过对杭长客专江西段轨道控制网测设搭接段典型数据的总结、分析，对比余弦法、置平法和四参数法的结果，认为余弦法更适合在国内高铁轨道控制网测段搭接中推广使用。

轨道控制网；区段搭接；数据处理

杭长客运专线是我国“四纵四横”客运网主骨架之一——沪昆客运专线的一部分，是一条承担区域间长途旅客为主、城际旅客为辅，同时兼顾与南北方向高速铁路之间转换客流的东西向客运专线。线路东起杭州东站，西至长沙南站，全长927 km，横贯浙江、江西、湖南3省，途经杭州、南昌、长沙3个省会城市和金华、衢州、上饶、鹰潭、新余、宜春、萍乡7个地级市以及浙江绍兴、江西抚州、湖南株洲3个地级市所辖部分区县。

一、几种搭接方式分析

目前工程实际中，全部按规范要求的搭接方式对搭接数据进行处理，即在搭接区段独立平差满足坐标较差≤±3 mm要求后，约束连续的1～3对CPⅢ进行平差计算，使用这种搭接方式的缺点是：①强行约束部分点位，可能由于点位兼容性不好，从而导致搭接区段平顺性差；②由于强行约束连续点位，而规范要求与CPⅢ点联测方向改正数不大于3″，如图1所示。

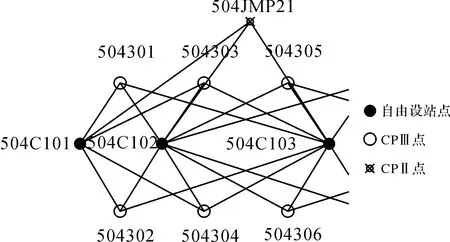
图1　区段搭接

当同时约束504301和504302这对点时，由于504C101与504C102站距离这两个CPⅢ点较近，一般为30 m左右，而504C103站距离较远，一般为120 m左右，由于X、Y坐标变化量(毫米级)相对于边长(米级)很小，其关系为

ΔX1=S1cos ΔL

(1)

式中，ΔX1为横向坐标变化量；S1为测站至目标CPⅢ点边长；ΔL为角度改正数。

计算出当504301、504302与原搭接点坐标较差增量差大于1 mm时，距离目标较近的504C101和504C102测站至504301、504302的角度改正ΔL就会超过4″，而距离目标较远的504C103站，当角度改正数ΔL为4″时，504301、504302两点的横向坐标已经变化超过4 mm，因此，本文认为规范关于轨道控制网角度限差的要求应以实际点位偏差为准，而不应该对长、短边全部采用一样的标准，这样不仅会导致短边精度过高，同样导致长边精度过低，无法真实反映测量精度。

为提高搭接段精度与轨道的平顺性，保证搭接段成果的唯一性，本文将对置平法、四参数法和余弦法3种搭接方式进行分析、对比。

1. 置平法

在轨道控制网进行区段搭接时，可以将搭接区段独立平差的结果分别作为两个刚体来看待，如何使两个刚体能够进行最优的匹配就是置平法要解决的问题。置平法就是在不改变搭接区域前后两段网形及精度的基础上，通过坐标转换的方式最终实现前后段的最佳匹配，因此其本质就是对搭接区段两次独立平差的坐标进行三参数转换。

如图2所示某点在原坐标系统坐标为(x,y)，通过平移(Δx,Δy)，然后旋转角度α后，在新坐标系中坐标为(x′,y′)，计算公式为

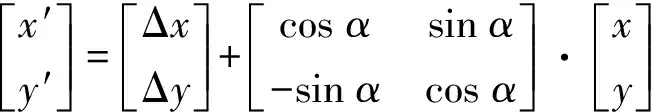
(2)

当搭接点超过2个以上时，就可以根据最小二乘法，求出转换参数(Δx,Δy)和α的无偏最优解，然后通过对搭接段坐标进行置平处理即三参数坐标转换，即可得到区段搭接后的唯一成果。

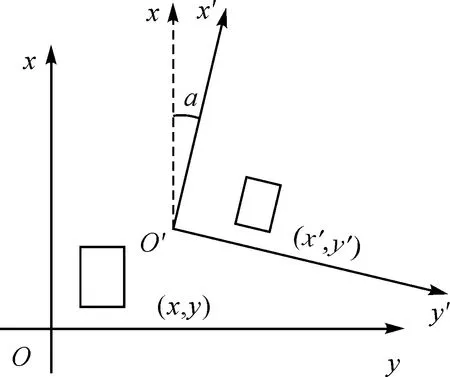
图2　坐标转换

2. 四参数法

根据规范要求，轨道控制网分段时需要至少预留6对CPⅢ点进行搭接处理，因此可以通过对置平法进行改进得到四参数法，即在旋转α、平移(Δx,Δy)的基础上增加尺度参数k，计算公式为

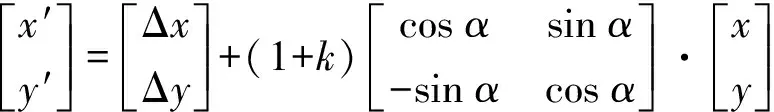
(3)

可以通过对搭接段连续的1～3对点作为转换基准，利用最小二乘法得到转换参数(Δx,Δy)、α和k的无偏最优解，然后通过对搭接段进行四参数坐标转换即可得到搭接后的唯一解。

3. 余弦法

余弦法是一种区段搭接的新方法，通过模拟几何中余弦函数图形对轨道控制网搭接段进行搭接处理，使用该搭接方式可以使搭接区段具有更好的平顺性，如图3所示。

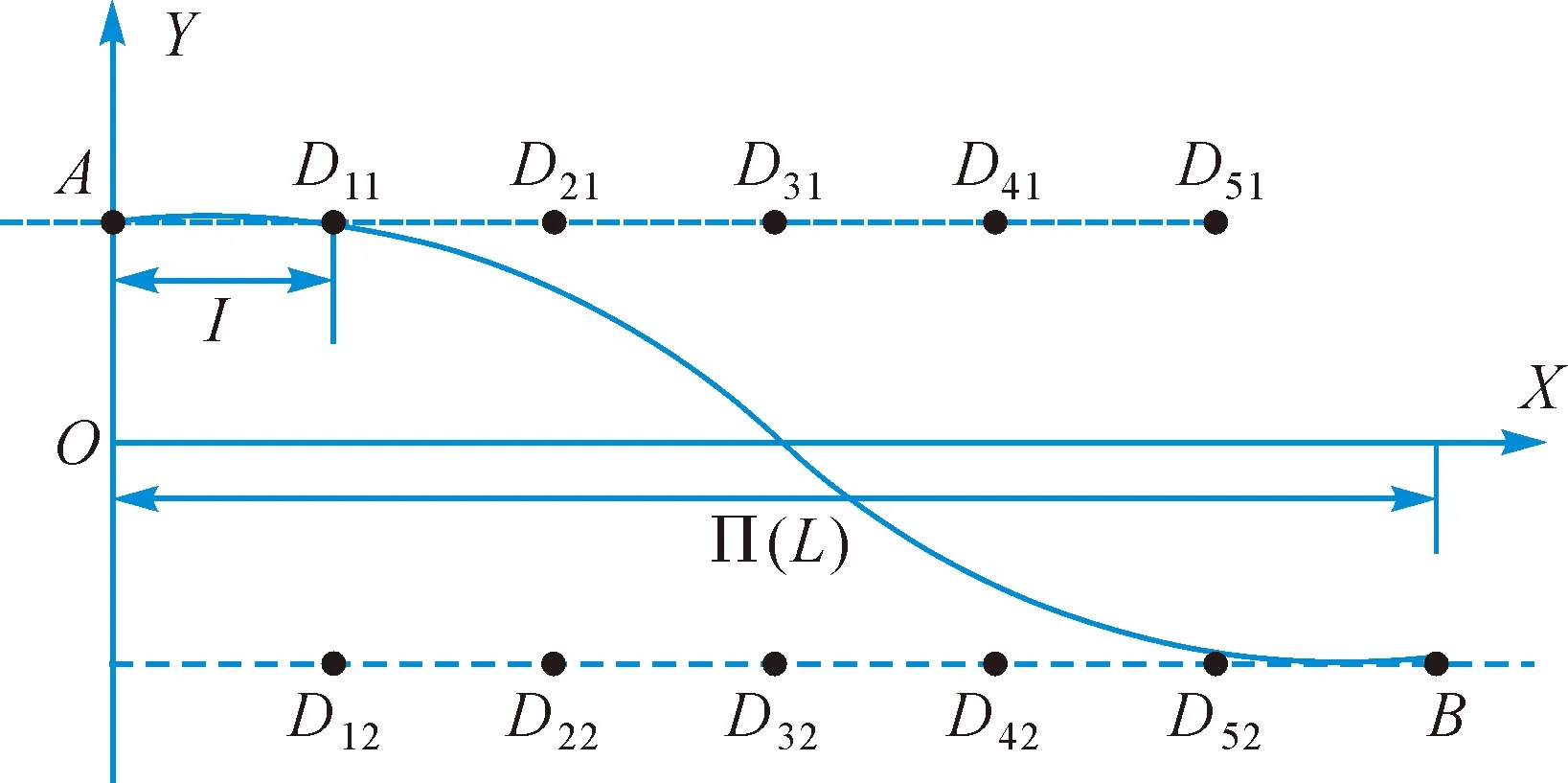
图3　余弦法示意图

D11、D21、D31、D41、D51为前一测段最后预留搭接的5个CPⅢ，其坐标分别为(X11,Y11)、(X21,Y21)、(X31,Y31)、(X41,Y41)、(X51,Y51)；D12、D22、D32、D42、D52为当前测段搭接的5个CPⅢ点，其坐标分别为(X12,Y12)、(X22,Y22)、(X32,Y32)、(X42,Y42)、(X52,Y52)；A为前一测段距离被搭接的5个CPⅢ点最近的一个CPⅢ点，B为当前测段距离被搭接的5个CPⅢ点最近的一个CPⅢ点，A、B两点间距离设为L。

假设各CPⅢ点之间的距离相等，均设为I。采用余弦函数平滑处理两测站的CPⅢ搭接点，则设余弦曲线为

Y=acosX+t

(4)

式中，a为振幅；t为余弦曲线在Y轴方向平移量。对两测段的搭接点采用余弦曲线加权平滑，赋予前一测段搭接点CPⅢ坐标的权为Y，后一测段搭接点CPⅢ坐标的权为1-Y。由于A、B为非搭接的CPⅢ点，其观测坐标在平滑处理前后不变。在A点时，X=0，Y=1；在B点时，X=180°，Y=0，因此可以得到如下方程组

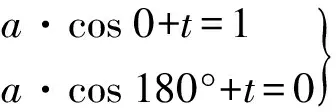
(5)

得到加权余弦函数表达式后，就可以求出轨道控制网中间5个CPⅢ搭接点的权，即

(6)

式中，L为搭接区段总长；I为搭接点间距离，实际计算中I可根据独立平差后的坐标计算出各点间的距离。最后按余弦加权法平滑即可得到轨道控制网各搭接CPⅢ点的唯一坐标

(7)

i=1,2,…,5

二、杭长客专搭接数据分析

杭长客专轨道控制网技术方案要求，搭接段独立平差坐标较差满足规范要求后，约束前一段连续的1～3对点进行平差计算，得到搭接段的新成果，本文随机选择3段搭接数据分别使用置平法、四参数法和余弦法对搭接段进行处理，并与按规范要求强制约束的结果进行对比，分析各搭接方法与规范要求的办法得到的成果是否存在显著差异，并通过坐标增量差来分析，哪种搭接方式得到的成果具有更好的平顺性，为保证搭接结果的一致性与可比性，均选用小里程连续的3对点作为参数计算及约束平差的起算数据，结果见表1、表2。

第1段置平法与搭接前两段独立平差成果及搭接后成果对比见表1。

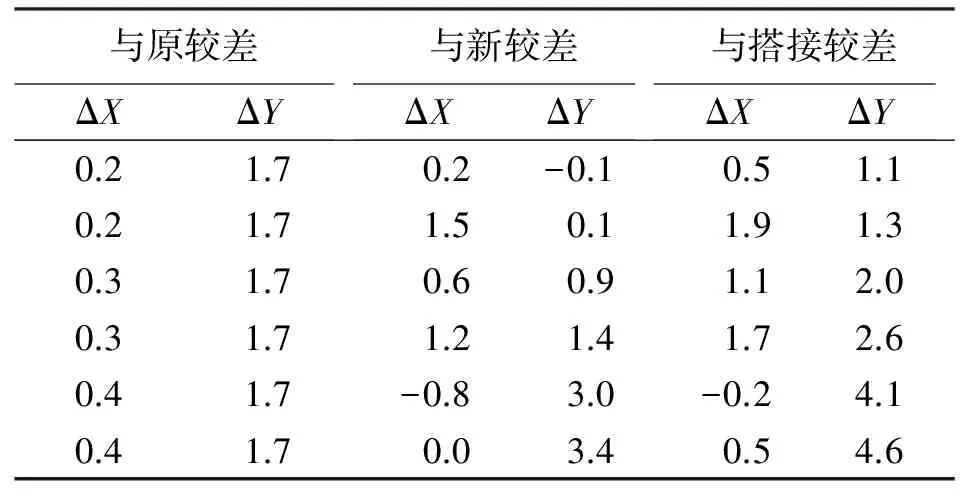
表1　置平法较差-1　mm

第2段置平法与搭接前两段独立平差成果及搭接后成果对比见表2。

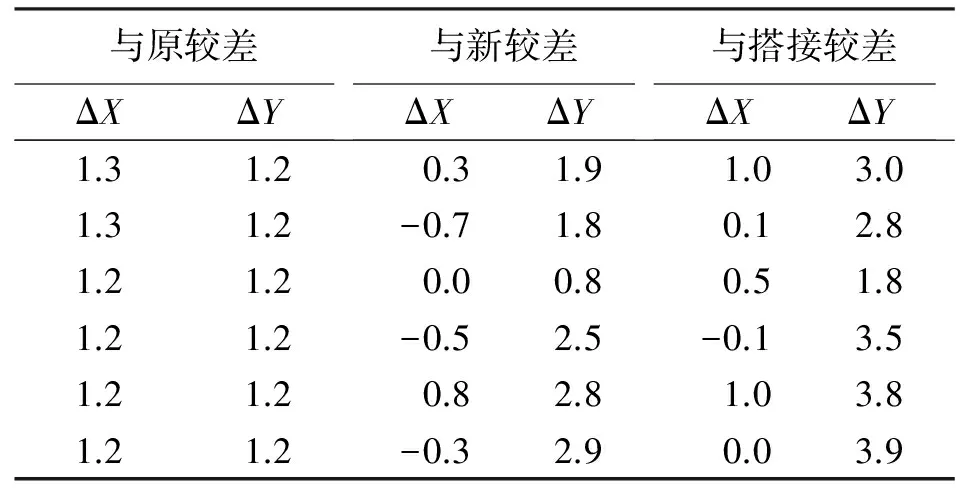
表2　置平法较差-2　mm

由上述两个对比表格可以看出，置平法得到的成果与搭接后成果有较大差异，最大值均无法满足3 mm限差要求，且呈现系统性偏差，基本上距离坐标转换点越远则坐标偏差越大。

第1段四参数法与搭接前两段独立平差成果及搭接后成果对比见表3。

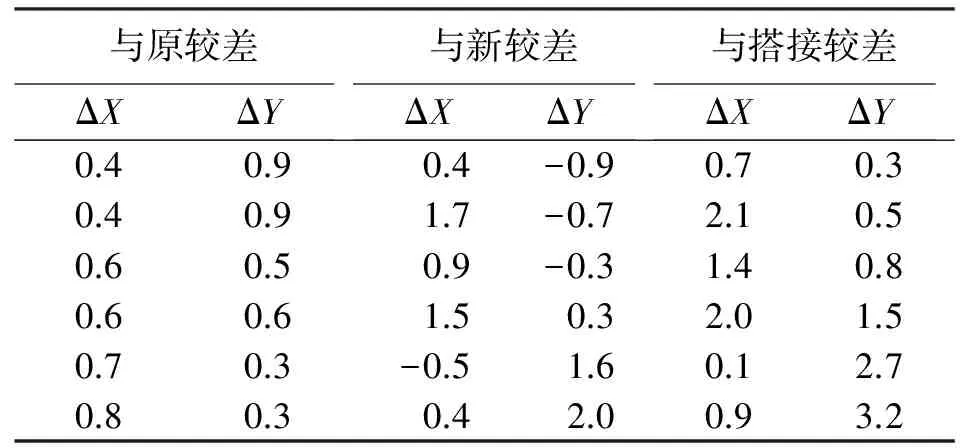
表3　四参数法较差-1　mm

第2段四参数法与搭接前两段独立平差成果及搭接后成果对比见表4。

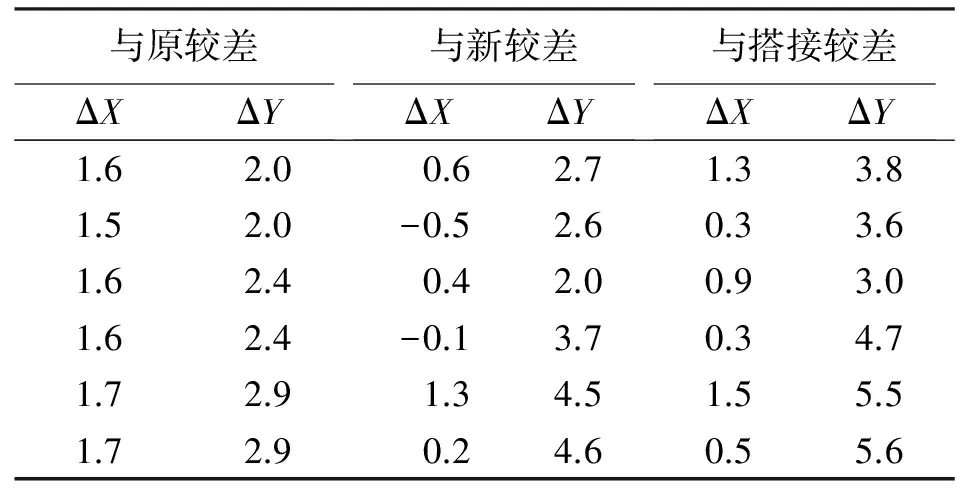
表4　四参数法较差-2　mm

由上述两个对比表格可以看出，四参数法在与独立平差及约束搭接点后成果较差均比置平法偏差更大，从转换参数对比来看，主要是由于搭接段点位较少，参与计算尺度k的点位不能真实反映搭接段尺度，从而导致转换成果比置平法偏差更大。

第1段余弦法与搭接前两段独立平差成果及搭接后成果对比见表5。

第2段余弦法与搭接前两段独立平差成果及搭接后成果对比见表6。

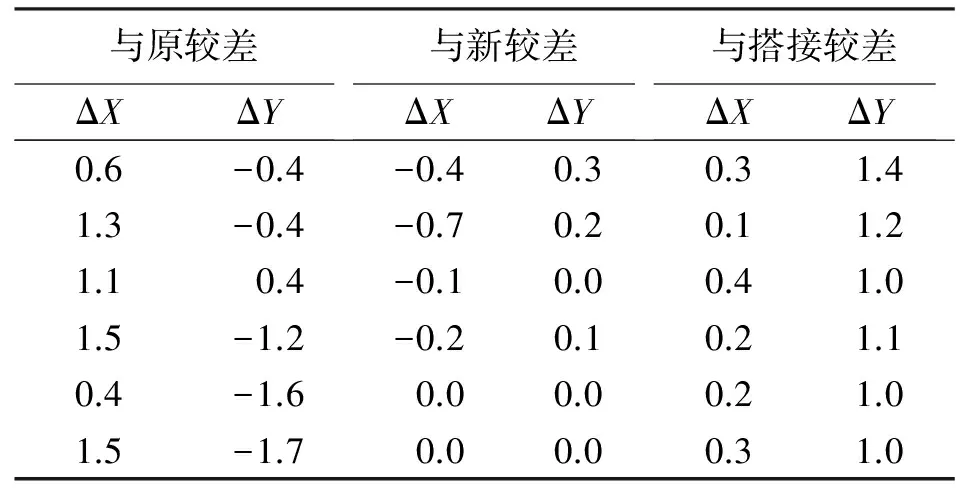
表6　余弦法较差-2　mm

通过上述两段对比，余弦法不仅与搭接前独立平差坐标较差较小，全部小于3 mm，且与约束平差搭接后坐标较差也满足3 mm限差要求，大部分较差在1 mm以下，即余弦法在3种搭接方式中与独立平差结果及搭接后成果的较差均为最小值，可以认为与实际偏差最小。

一般认为新测设结果与实际点位具有更好的一致性，因此可以认为新测设的独立平差结果为真实值，而搭接后成果为拟合值，通过对搭接结果与独立平差结果的坐标增量差对比各搭接方式的平顺性，坐标增量差越小，则认为对线路平顺性影响越小。坐标增量差计算公式为

(8)

统计结果如下

第一段3种搭接方式坐标增量差见表7。

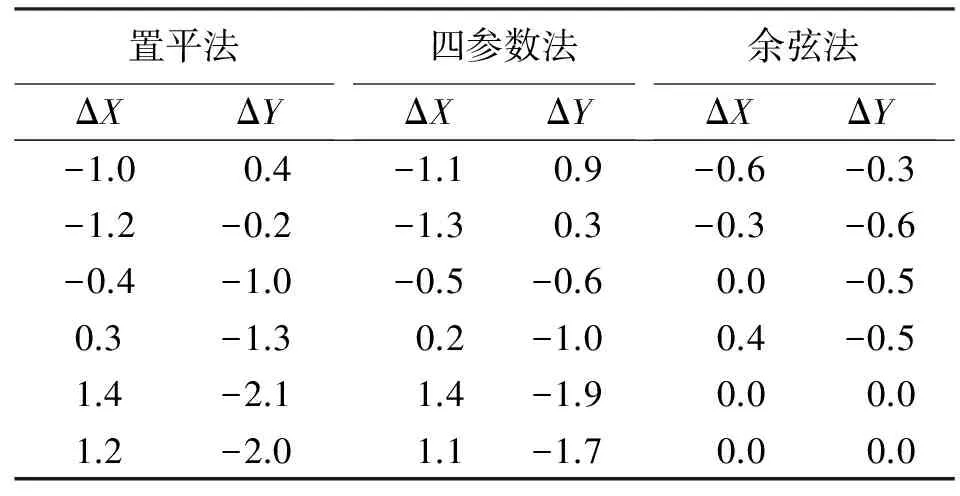
表7　坐标增量差-1　mm

第二段3种搭接方式坐标增量差见表8。

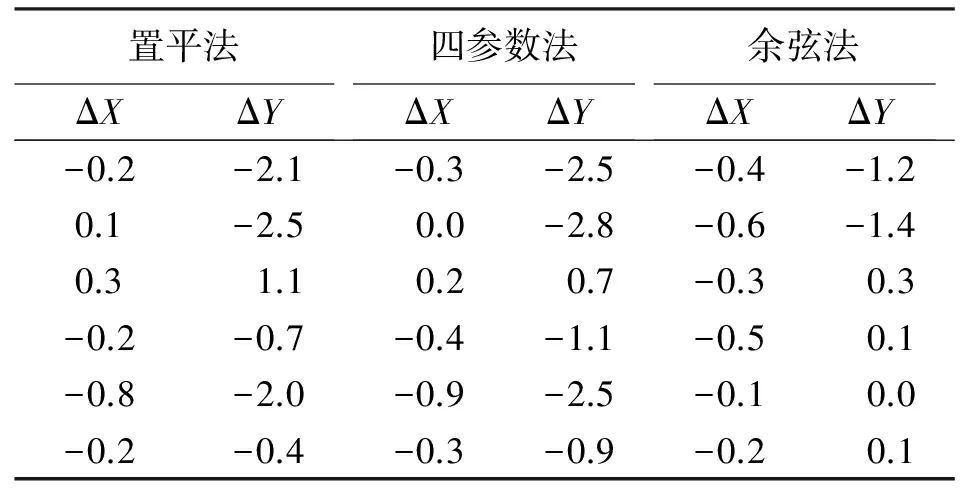
表8　坐标增量差-2　mm

由上述统计数据可以看出，余弦法在3种搭接方式中坐标增量差最小，即在保证前后顺利搭接的同时，满足对线路平顺性影响最小的要求。

通过对以上数据的对比、分析发现，在搭接段满足规范要求3 mm限差时，采用余弦法进行搭接处理，不仅能够使搭接段内所有点位的坐标较差较小，而且能够使不同时期测量的数据对线路平顺性的影响降到最低，因此本文推荐使用余弦法对搭接段进行处理。

三、结束语

高速铁路因其具有良好的时效性、安全性和舒适性，成为陆上公共交通的首选，同时其技术创新也在不断地对周边产业产生积极的影响，因而得到世界各国的大力支持和发展，而轨道控制网的精度对高铁轨道的安全性、平顺性起着决定性作用，本文通过对置平法、四参数坐标转换法和余弦法的综合对比分析，认为余弦法在轨道控制网区段搭接时更能保证线路的平顺性，因此推荐使用余弦法作为轨道控制网区段搭接的方式。

[1]铁道部建设管理司.高速铁路工程测量规范：TB 10601—2009[S].北京：[s.n.]，2009.

[2]周东卫.高速铁路轨道控制网CPⅢ精密测量若干问题探讨[J].铁道勘察，2011(5)：5-8.

[3]石德斌，王长进，李博峰.高速铁路轨道控制网测量和数据处理探讨[J].铁道工程学报，2009(4)：26-30.

[4]安国栋.高速铁路精密工程测量技术标准的研究与应用[J].铁道学报，2010(4)：98-103.

[5]武瑞宏.高速铁路精密控制测量网有关问题的探讨[J].铁道勘察，2008(5)：1-3.

[6]李成.高速铁路控制测量中需要注意的若干问题[J].科技资讯，2011(8)：64-65.

[7]潘正风，徐立，肖进丽.高速铁路平面控制测量的探讨[J].铁道勘察，2005(5)：1-3.

[8]李明领.高速铁路无砟轨道CPⅢ控制网建立与精度控制[J].铁道标准设计，2010(1)：84-86.

[9]郝亚东，周建郑，孙请娟，等.高铁无砟轨道CPⅢ控制网测量[J].铁道工程学报，2010(11)：38-42.

[10]范亚军，黄腾，刘岭，等.高铁无砟轨道基准点平面测量方法[J].测绘工程，2012(2)：58-62.

On the Method of Sections Overlap in Hangchang High-speed Railway Track Control Network

LIU Peiqing

柳培清.杭长客专轨道控制网区段搭接方式探讨[J].测绘通报，2016(10)：89-92.DOI:10.13474/j.cnki.11-2246.2016.0337.

2016-01-29

柳培清(1973—)，男，高级工程师，研究方向为工程测量。E-mail：sky_wxw@qq.com

P258

B

0494-0911(2016)10-0089-04