JLCORS网络参考站坐标时间序列噪声类型分析

刘俊清，肖辉峰，张晨侠，丁　广

(1. 吉林大学地球探测科学与技术学院，吉林 长春 130026； 2. 吉林省地震局，吉林 长春 130117； 3. 北京麦格天宝科技股份有限公司，北京 100029)



JLCORS网络参考站坐标时间序列噪声类型分析

刘俊清1,2，肖辉峰3，张晨侠2，丁广2

(1. 吉林大学地球探测科学与技术学院，吉林 长春 130026； 2. 吉林省地震局，吉林 长春 130117； 3. 北京麦格天宝科技股份有限公司，北京 100029)

利用吉林省连续运行参考站网络(JLCORS)近3年的观测资料，使用GAMIT/GLOBK软件进行后处理，解算时用吉林省周边IGS及陆态网络站点作为控制点，获得41个站单日松弛解的坐标时间序列。用最大似然法拟合经典的噪声模型，根据噪声模型是否能够取得似然函数的最大值，获得不同噪声模型及其组合的参数估计。结果表明，JLCORS全部参考站坐标时间序列噪声含有幂律噪声及白噪声，可用二者的组合噪声模型来描述，不含带通滤波噪声及各阶高斯-马尔科夫噪声。幂律噪声模型部分的谱指数集中分布在-2附近，表明幂律噪声的特例随机游走噪声占有主导地位。

CORS；IGS；陆态网；噪声模型

地球动力学是建立在观测试验基础上的一门学科，观测数据不可避免地存在误差、不稳定和不确定等非地壳构造因素的影响[1-3]，误差性质及分离方法的研究一直是地学工作者的一项重要工作。由于地壳构造活动是一个非常缓慢的过程，地壳监测时间序列跨度很长，通常是几年甚至几十年，这就意味着观测值中含有大量的与时间相关的误差，而且误差源也可能随着时间变化[4-6]。如在多年的观测过程中，仪器老化、更换及观测墩标不稳定等，均与时间具有相关性，都会在观测数据时间序列中产生误差。随着研究的深入，逐渐发现这类与时间相关的误差的一些统计规律，可用白噪声(white noise，WN)和幂率噪声(power law noise，PLN)的组合模型进行很好的模拟[4]。白噪声可以通过增加观测次数来降低影响，幂率噪声却无法消除,只能通过噪声相对准确的统计关系，在数据处理时建立数学模型来消除。

目前，很多国家建立了国家级、区域级的CORS网络，主要用于测绘工作中。建站标准及其选址要求都低于地壳运动研究的标准，大部分站使用土层标墩建设规范，甚至建在了建筑物顶部。这样的观测环境会给GNSS观测带来很多误差信号，对不同用途的观测要求，需要相应地选择计算模型消除误差，这就需要对误差性质进行研究，获得其统计表达式，然后引入数据处理软件。在信号研究中，误差信号采用噪声模型描述，本文应用最大似然法对吉林省连续运行参考站网络(Jilin Continuously Operating Reference Station，JLCORS)参考站坐标时间序列噪声性质进行研究。

一、数据资料及噪声分析方法

1. JLCORS概况

CORS系统理论源于20世纪80年代，经过多年的发展，现在连续运行参考站系统(CORS)能够常年连续不断地运行，服务于高精度中短期天气状况的数值预报、变形监测、地震监测、地球动力学等[7]。它不仅满足了各种测绘、基准的需求，还满足了地震地壳形变监测需求。目前，很多国家建立了国家级、区域级的CORS网络[8]，JLCORS由吉林省测绘地理信息局建设(如图1所示)，图中黑色正三角表示设计参考站位置。JLCORS是我国地区(省)级的连续运行的参考站网络系统，它将在全省范围内建立的永久性参考站通过网络互联，构成新一代的网络化的大地测量系统，将GNSS技术综合应用于吉林省的大地测量、工程测量、气象监测、地震监测、地面沉降监测及城市地理信息系统等领域，2010年12月已经建成49个站并投入运行。

2. GNSS后处理软件

GAMIT/GLOBK是国际上三大高精度GNSS后处理软件之一，由美国麻省理工学院(MIT)和斯克里普斯海洋研究所(SIO)联合开发，主要应用于分析研究地壳形变、高精度GPS测量数据处理等领域。GAMIT软件处理双差观测量，采用最小二乘算法进行参数估计。GAMIT软件主要由以下几个模块构成：ARC(轨道积分模块)、MODEl(组成观测方程)、SINCI N(单差自动修复周跳)、DBCI N(双差自动修复周跳)、CVIEW(人工交互式修复周跳)、SOI VE(最小二乘解算模块)、DFMRG(数据融合模块)、FXDRV(生成批处理文件)、GI OBK(运用卡尔曼滤波进行网平差)等。

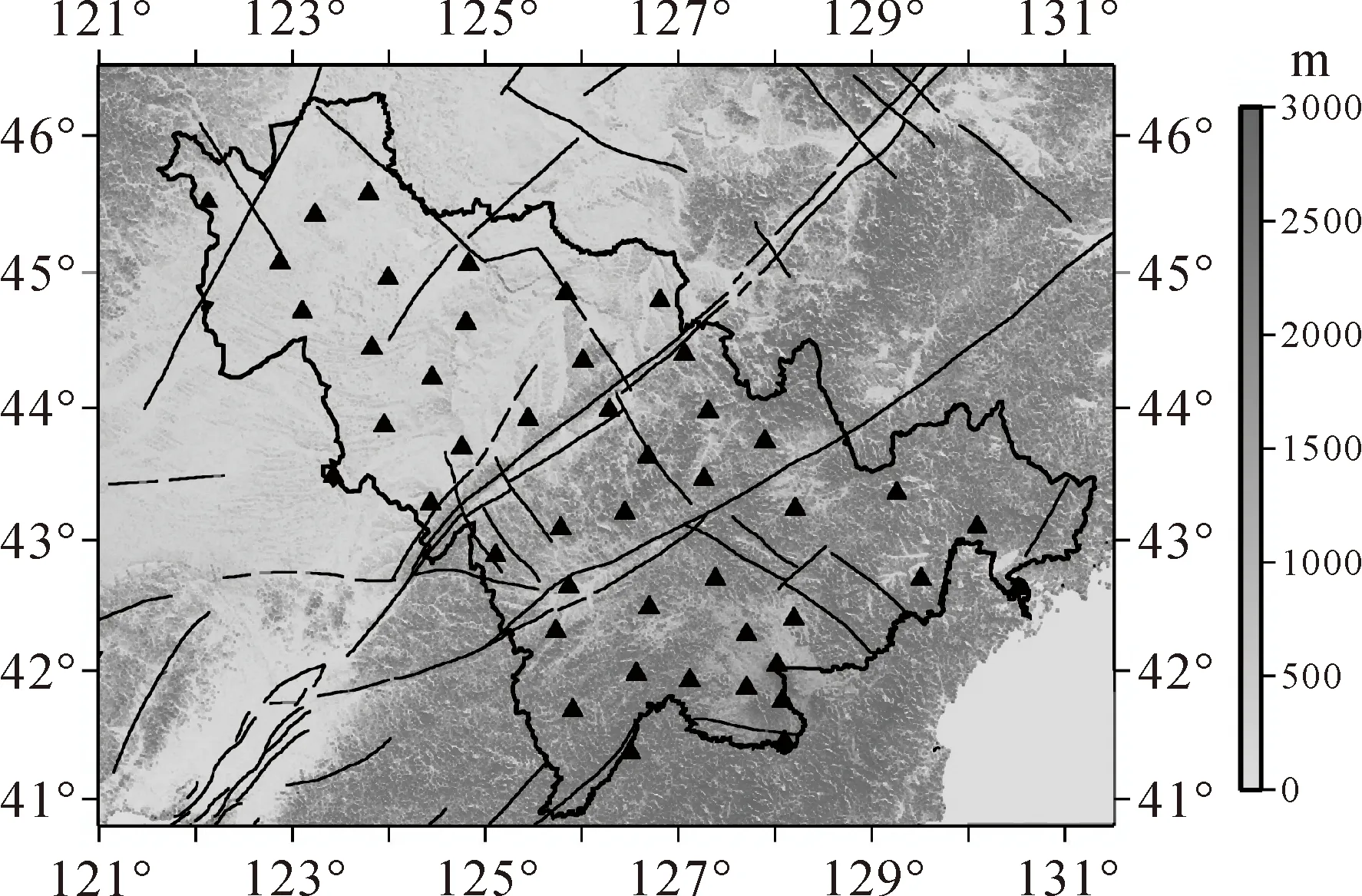
图1　JLCORS基准站分布

3. 时间序列噪声分析方法

时间序列是动态测试中被观测量在一定的幅值范围内随时间出现的一系列随机数据。频谱分析和波形分析是最重要和最基本的方法。频谱分析可求得时间序列的幅值谱、相位谱、功率谱和各种谱密度等，波形分析也即时间域分析，与频谱分析可用傅里叶变换相互转换。功率谱技术和最大似然法分别在频率域和时间域对大地测量手段时间序列的噪声分析表明，时间序列包含的噪声类型非常复杂，如白噪声、幂律噪声、高斯-马尔可夫噪声、带通滤波噪声等，可以是仅含有一种噪声，也可以是多种噪声的组合。相应地用这些噪声的数学模型拟合时间序列来求解噪声参数。

最大似然估计(MLE)[9]可以同时获得时间相关的噪声模型的所有参数，经过试验证实，MLE方法不但可以最大限度地发现一列随机数据包含的噪声，而且能准确计算出这些噪声的功率谱，与谱分析所得的结果能够精确符合。本次研究应用MLE方法进行时间序列噪声分析。

(1) 最大似然估计

最大似然估计的公式为

(1)

在实际中，C是一种或多种噪声统计模型的组合，可以用下式表示

(2)

式中，σ为噪声模型的幅度；R为各噪声模型的协方差矩阵。

式(2)取自然对数后可得

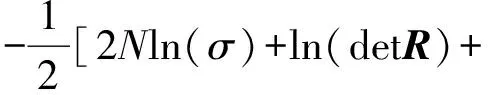
(3)

对σ求微分可得

(4)

通过上述变换，可以把多维问题转化为一维问题，在解似然方程中，采用上述单纯形法。

(2) 噪声模型

根据地球物理观测所包含噪声统计规律，构造出如下模型，在噪声分析中拟合时间序列噪声。

① 幂律噪声

因许多地球物理过程可以用一个幂律过程来描述，GNSS时间序列噪声也具有这样的幂律性质，即噪声功率谱Px(f)与其对应的噪声频率f之间存在某种幂次关系

(5)

(6)

式中，Px为功率谱；f为噪声频率；P0、f0为常数；κ为谱指数；σpl为噪声幅度。谱指数分布范围通常为(-3，1),稳定过程谱指数为(-1，1)，不稳定过程谱指数为(-3，-1)。随机过程分为稳定过程和不稳定过程，不稳定过程在低频部分通常有较大的功率，而在高频部分有负的谱指数，通常负谱指数分布在开区间(-3，-1)内，其中白噪声的谱指数κ=0，闪烁噪声的谱指数κ=-1、κ=1。类随机游走过程的谱指数分布在区间(1，3)内,如典型的随机游走噪声谱指数κ=2。

② 高斯-马尔可夫噪声

一阶高斯-马尔可夫噪声统计模型可用下式表示

(7)

一阶高斯马尔可夫信号可用下面微分方程表示

(8)

式中，Px为功率谱；f为噪声频率；P0、f0为常数；κ为谱指数。

③ 带通噪声

带通信号是周期过程，在地球物理现象中常常是由季节变化引起，公式如下

(9)

式中，P为功率谱；f为噪声频率；f1为常数；κ为谱指数；σbp为噪声幅度。

二、数据处理结果及噪声性质分析

在获得JLCORS坐标时间序列时，使用的数据策略是首先在GAMIT部分获得所有站点的单日松弛解。在计算中选用IGS站(CHAN、BJFS、KHRJ、AIRA等)和陆态网站(HLAR、SUIY、JIXN、CHUN等)作为控制点，适当紧约束控制站坐标而对JLCORS站给予较松弛的约束。在GLRED模块，先获得所有点的时间序列，对数据结果进行检查，利用GLOBK将SPOAC给出的全球单日松弛解和计算所得的区域单日松弛解进行综合平差计算，在此基础上通过IGS核心站求解相对于全球参考框架ITRF2008的相似变换参数，从而获得ITRF2008下的单日解。最终获得JLCORS参考站坐标时间序列，分别为E(东向)、N(北向)，U(垂直方向)，如图2所示。

数据处理采用CATS程序[10]，其核心算法是参数估计中的最大似然估计。计算时，拟合多个经典噪声统计模型到观测时间序列，通过构造和求解似然函数，获得最佳的噪声模型，而且可以同时求解噪声模型中的所有待估参数。计算是一个迭代的过程，为提高处理速度，CATS在计算过程中引入1个标量angle，即一个帮助计算的辅助量，没有物理意义，通过angle的增加计算出似然函数的最大似然值，然后计算噪声模型中各个参数的值。

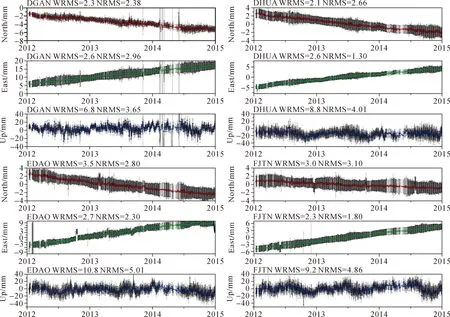
图2　JLCORS部分参考站(DGAN、DHUA、EDAO、FJTN)坐标时间序列

通过对幂律噪声、闪烁噪声、随机游走噪声及它们各自和白噪声的组合进行似然函数值的计算，随机游走噪声和白噪声的组合能取得最大的似然函数值。表1是观测站N-S向坐标时间序列迭代后求得的噪声组合模型中各个参数的估计值。表中σpl表示利用式(5)的幂律噪声模型计算的噪声幅度，σbp表示利用式(9)的带通滤波模型计算的噪声幅度，SD是各模型计算结果的标准差。表中带通滤波噪声很多站通过迭代后，似然函数不收敛，没有计算结果，用“—”表示，其中有几个站有迭代结果，其标准差也非常大，显然是错误的结果。这样的情况说明序列中不含带通滤波噪声，这类噪声是由于季节更替产生的，存在于大多地球物理观测资料中，在JLCORS参考站中却没有解算结果，所有站坐标时间序列均受白噪声的影响。由于幂律噪声模型覆盖的噪声类型范围很广，所有站结果可见主要含有幂律噪声。

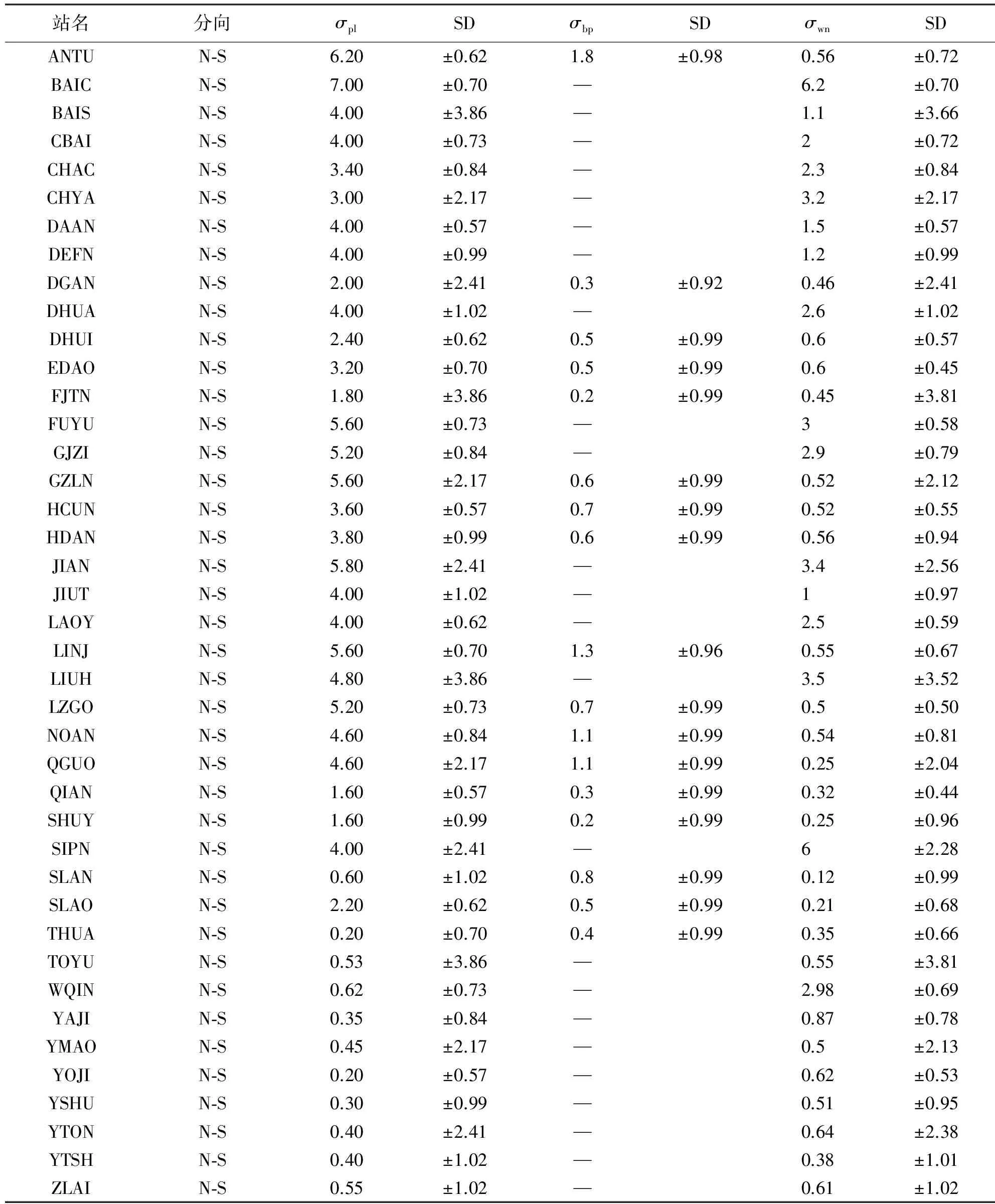
表1　JLCORS参考站噪声参数分析结果

用幂律噪声加白噪声的组合噪声模型拟合时间序列可获得最大的似然函数值，同时获得每个参考站所有分向幂律噪声谱指数，分布区间为[-2.32，-1.71]，谱指数集中在κ=-2附近(如图3所示)，此时为幂律噪声的特例——随机游走噪声。由此可见GNSS时间序列噪声占主导地位的应该是随机游走噪声。研究地壳运动的基岩站，随机游走噪声的幅度很小，较短的时间序列很难监测到，特别是在全球网解算数据时很大的共模误差会将其淹没[11]。本次研究的参考站网为区域级别，空间相关的误差不会产生，有利于计算随机游走噪声的幅度。

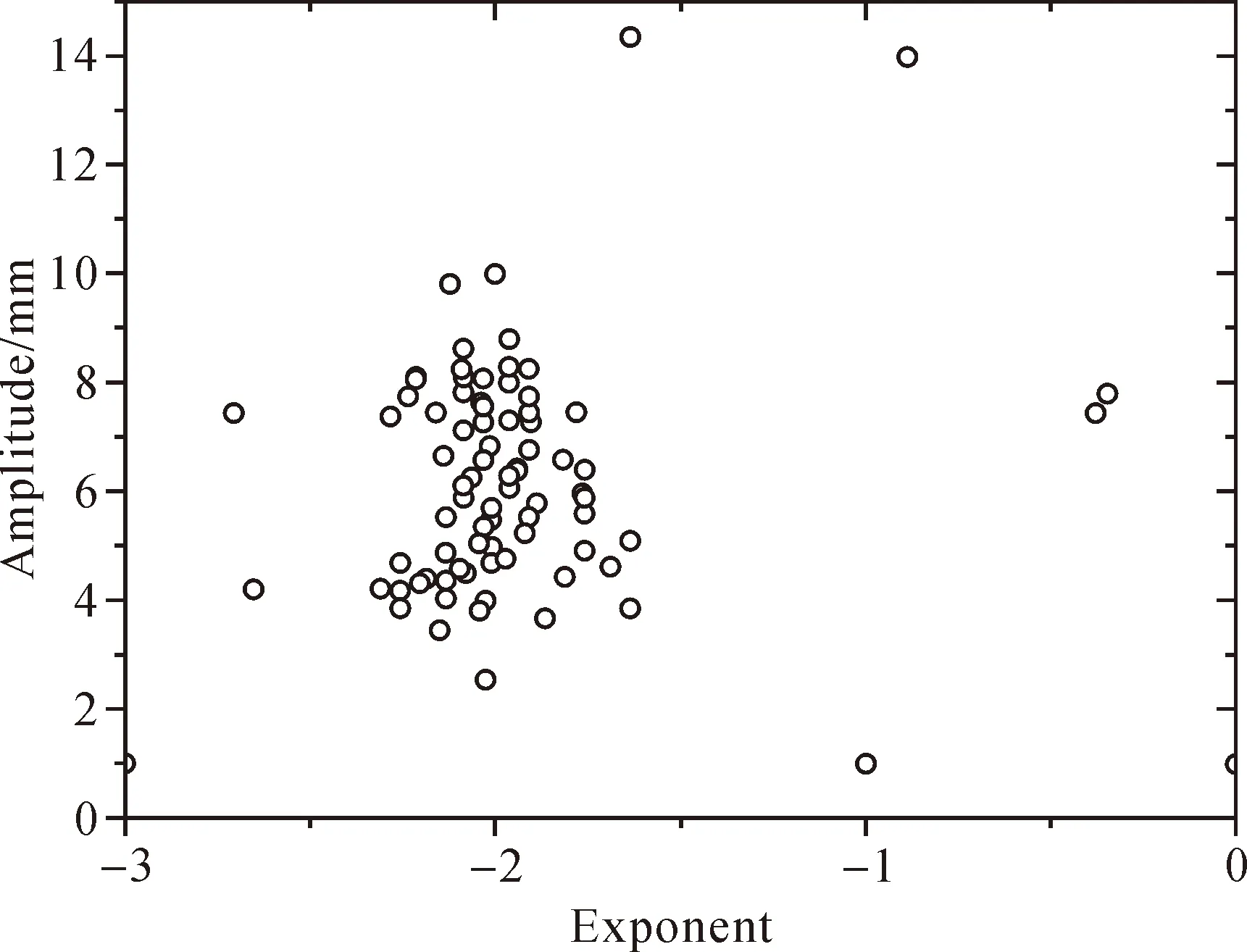
图3　JLCORS东西方向谱指数和噪声幅度的关系

三、结束语

GNSS观测资料结果解算后在结果中包含很多误差信息，如GNSS整个观测系统的误差、解算过程的模型误差、观测墩的非构造误差等。在信号处理过程中，这些信号可看作是随机噪声。本文通过最大似然法进行参数估计，根据JLCORS参考站坐标时间序列与经典噪声模型拟合，估计各个噪声模型的参数，来确定观测结果的误差信息可用哪种噪声模型来描述。该计算过程使用噪声分析软件CATS来实现，经过分析表明，所有参考站均可用幂律噪声和白噪声的组合模型来描述，根据谱指数分布区间，幂律噪声中的特殊情况之一的随机游走噪声占主导地位。也就是说JLCORS参考站坐标时间序列的误差信息可用随机游走噪声和白噪声的组合来描述。

[1]王敏, 沈正康, 董大南. 非构造形变对 GPS 连续站位置时间序列的影响和修正[J]. 地球物理学报, 2005, 48(5): 1045-1052.

[2]田云锋, 沈正康. GPS 坐标时间序列中非构造噪声的剔除方法研究进展[J]. 地震学报, 2009, 31(1): 68-81.

[3]黄立人, 符养. GPS 连续观测站的噪声分析[J]. 地震学报, 2007, 29(2): 197-202.

[4]LANGBEIN J. Noise in Two-color Electronic Distance Meter Measurements Revisited[J]. Journal of Geophysical Research: Solid Earth (1978—2012), 2004, 109(B4).DOI:10.1029/2003JB002819.

[5]LANGBEIN J, JOHNSON H. Correlated Errors in Geodetic Time Series: Implications for Time-dependent Deformation[J]. Journal of Geophysical Research: Solid Earth (1978—2012), 1997, 102(B1): 591-603.

[6]MAO A, HARRISON C G, DIXON T H. Noise in GPS Coordinate Time Series[J]. Journal of Geophysical Research: Solid Earth (1978—2012), 1999, 104(B2): 797-816.

[7]杜向锋, 张兴福, 张永毅. CORS 测量成果转换的一步法及其精度分析[J]. 测绘通报, 2015(7): 23-26.

[8]郑立平. 港口镇单参考站 CORS 系统建设及应用[J]. 测绘通报, 2011(1): 43-45.

[9]莫惠栋. 最大似然法及其应用[J]. 遗传, 1984, 6(5): 42-48.

[10]WILLIAMS S D. CATS: GPS Coordinate Time Series Analysis Software[J]. GPS solutions, 2008, 12(2): 147-153.

[11]BOS M, FERNANDES R, WILLIAMS S, et al. Fast Error Analysis of Continuous GPS Observations[J]. Journal of Geodesy, 2008, 82(3): 157-166.

Analysis of the Noise of Coordinate Time Series from JLCORS Network Reference Stations

LIU Junqing,XIAO Huifeng,ZHANG Chenxia,DING Guang

刘俊清，肖辉峰，张晨侠,等.JLCORS网络参考站坐标时间序列噪声类型分析[J].测绘通报，2016(10)：1-5.DOI:10.13474/j.cnki.11-2246.2016.0316.

2015-12-15

地震科技星火计划(XH14016Y)

刘俊清(1977—)，男，博士生，高级工程师，主要从事地震火山监测预报研究。E-mail: lunwen_98@126.com

P228

B

0494-0911(2016)10-0001-05