锂离子电池组风冷结构设计与优化*

白帆飞，陈明彪，宋文吉†，冯自平

（1. 中国科学院广州能源研究所，广州 510640；2. 中国科学院可再生能源重点实验室，广州 510640；3. 广东省新能源和可再生能源研究开发与应用重点实验室，广州 510640；4. 中国科学院大学，北京 100049）

锂离子电池组风冷结构设计与优化*

白帆飞1，2，3，4，陈明彪1，2，3，宋文吉1，2，3†，冯自平1，2，3

（1. 中国科学院广州能源研究所，广州 510640；2. 中国科学院可再生能源重点实验室，广州 510640；3. 广东省新能源和可再生能源研究开发与应用重点实验室，广州 510640；4. 中国科学院大学，北京 100049）

本文运用正交试验法设计电池组风冷结构参数优化试验方案，研究电池组间距递减幅度、上集流板倾斜角度、下集流板倾斜角度等结构参数的变化对电池组温度场、流场以及进出口压差的影响，确定了电池组最优结构：间距递减幅度0.3 mm、上集流板倾斜0°、下集流板倾斜5°；运用实验和仿真的方法，研究具有最优结构的电池组分别在0.5 C、1 C、2 C倍率放电过程的温度变化特性，电池组的最高温度及温度场一致性均能满足要求。

锂离子电池组；风冷结构；正交试验；数值模拟

0 引 言

锂离子电池组的最高温度、温度场的均匀性是电池组热管理系统的重要评价指标［1］。电池组采用强制风冷时，空气进出口压差反映了电池组内部的阻力大小，决定了风机的功率需求。为保证电池组正常输出功率，延长循环寿命，同时降低风机能耗，应综合考虑电池组内风道宽度、上下集流板倾斜角度等结构因素对温度场、压力场的影响［2-5］。

本文利用正交试验法对电池组内风道宽度（即电池组间距）、上集流板倾斜角度、下集流板倾斜角度这三个结构参数优化配组，采用直观分析法以电池组最高温度、模块间最大温差和进出口压差为评价指标对各结构参数的作用规律进行分析。

1 电池组的参数选择及正交表设计

研究采用的单体电池为铝塑膜外包方形LiFePO4/C动力电池，额定电压3.2 V，额定容量20 A·h，尺寸170 mm×7 mm×230 mm，质量为0.545 kg，电池的其他参数如表1所示。

表1 锂离子电池参数Table 1 Parameters of lithium-ion battery

如图1，锂离子电池组由12个串联的电池模块依次排列组成，每个电池模块由两个紧贴的电池单体并联而成，电池组的电压为 38.4 V，容量为40 A·h。电池组内模块平均间距为5 mm，出入口均为50 mm×170 mm的矩形，电池组外观尺寸330 mm×233 mm×170 mm。电池组采用并行通风、强制风冷的形式，以更好地控制电池的温升并保持电池组温度分布的均匀性。为使冷却风机不工作时锂离子电池组仍能短时间利用自然对流换热，冷却空气采用由下往上的流向［6］。

图1 锂离子电池组结构示意图Fig. 1 Structure of the experimental lithium-ion battery pack

正交试验设计是研究多因素多水平的一种设计方法，是根据正交性从全面试验中挑选出部分有代表性的点进行试验，是一种高效率、快速、经济的实验设计方法［7］。正交设计中，实验变量称为因素，各因素的取值称为水平。本文选择电池组间距的递减幅度ΔL、上集流板倾斜角度θu、下集流板倾斜角度θl三个参数为因素，每个因素取3个水平，具体见表2。

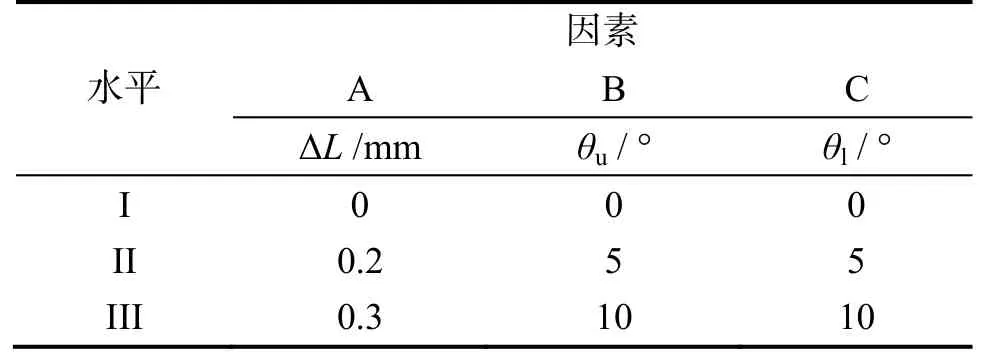
表2 因素水平表Table 2 Factors and levels of orthogonal experiment

由于各因素之间无交互作用，正交试验设计见表3，实验编号为No.1～No.9，采用FLUENT软件仿真计算。

冷却空气在电池组内部流动过程中涉及分流、转弯、汇合等复杂过程，流场脉动以及在换热表面的分离不可避免，更接近于湍流，因此仿真求解选用k-ε湍流模型。入口空气速度3 m·s-1，温度300 K；压力出口，0 Pa，温度300 K；电池与空气接触面流-固耦合，无滑移；电池组外壳绝热。电池单体以2 C倍率放电时生热速率为61 045 W·m-3。考察各种参数的作用规律时可不考虑时间影响，采用稳态计算求解器，求得不同结构电池组最高温度 Tmax、模块间最大温差ΔTmax和进出口压差Δp。仿真计算结果见表3。

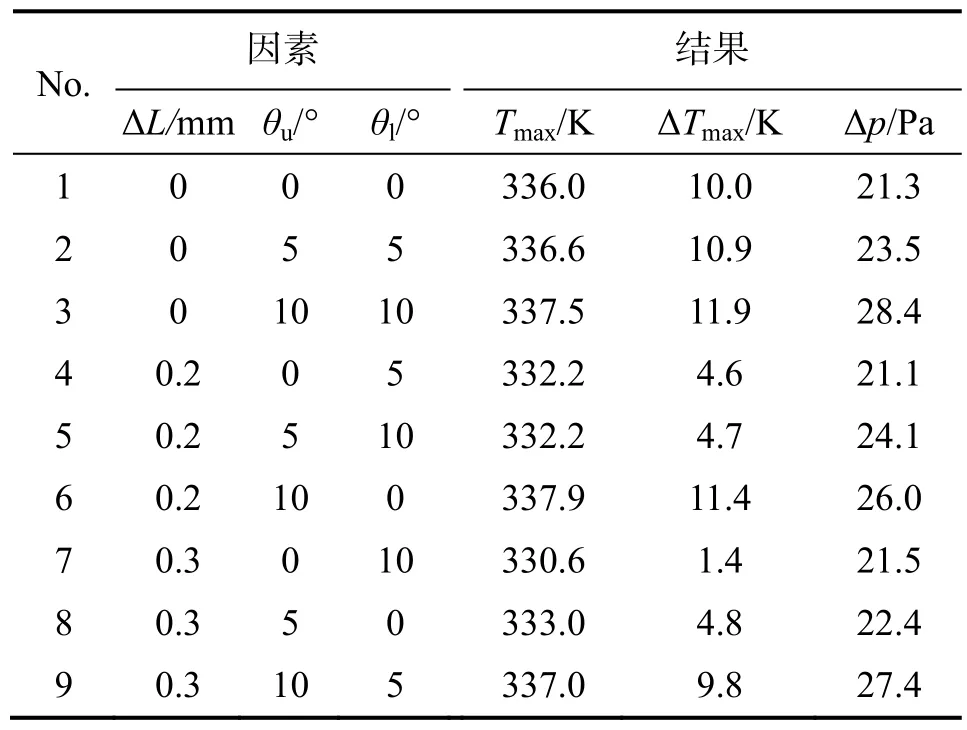
表3 正交试验设计及仿真结果Table 3 Orthogonal experiment design and simulation results

2 正交分析及优化

表2中ΔL的水平I、II、III分别出现在三组试验No.1～No.3、No.4～No.6、No.7～No.9中。记9次试验得到的各项指标值依次为y1～y9，取水平I、II、III的平均值：k1=（y1+ y2+ y3）/3，k2=（y4+ y5+ y6）/3，k3=（y7+ y8+ y9）/3。令R=max｛k1，k2，k3｝ - min｛k1，k2，k3｝，R即为极差。因为在三组试验No.1～No.3、No.4～No.6、No.7～No.9中，θu和θl的三个水平各出现一次，所以这种变动是平等的，因此可以认为R是由于ΔL的水平变动引起的［8］。极差R反映了各因素水平变动对试验结果影响的大小，极差越大表示该因素的水平变化对试验结果影响越大。表4列出了三个评价指标 Tmax、ΔTmax、Δp所对应的不同因素的极差。各因素对评价指标的影响趋势如图2。

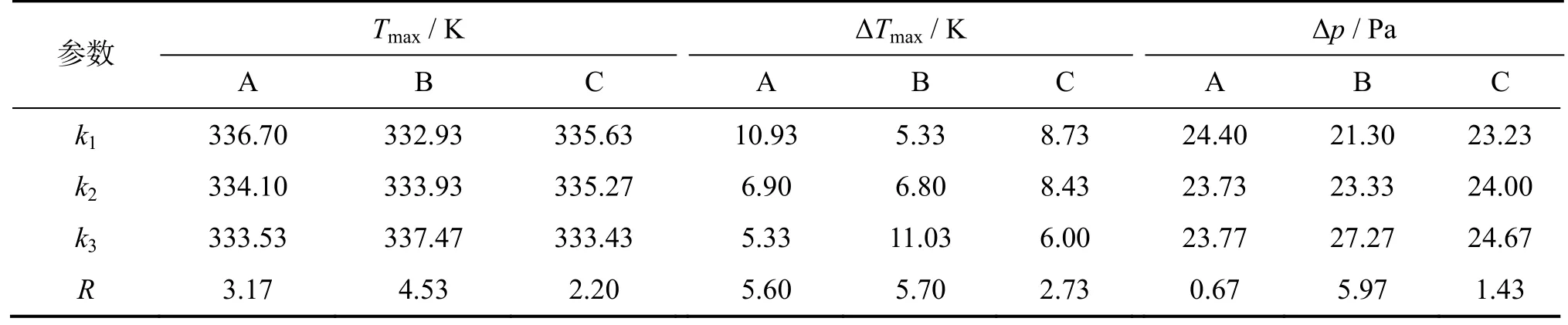
表4 极差分析Table 4 Range analysis data

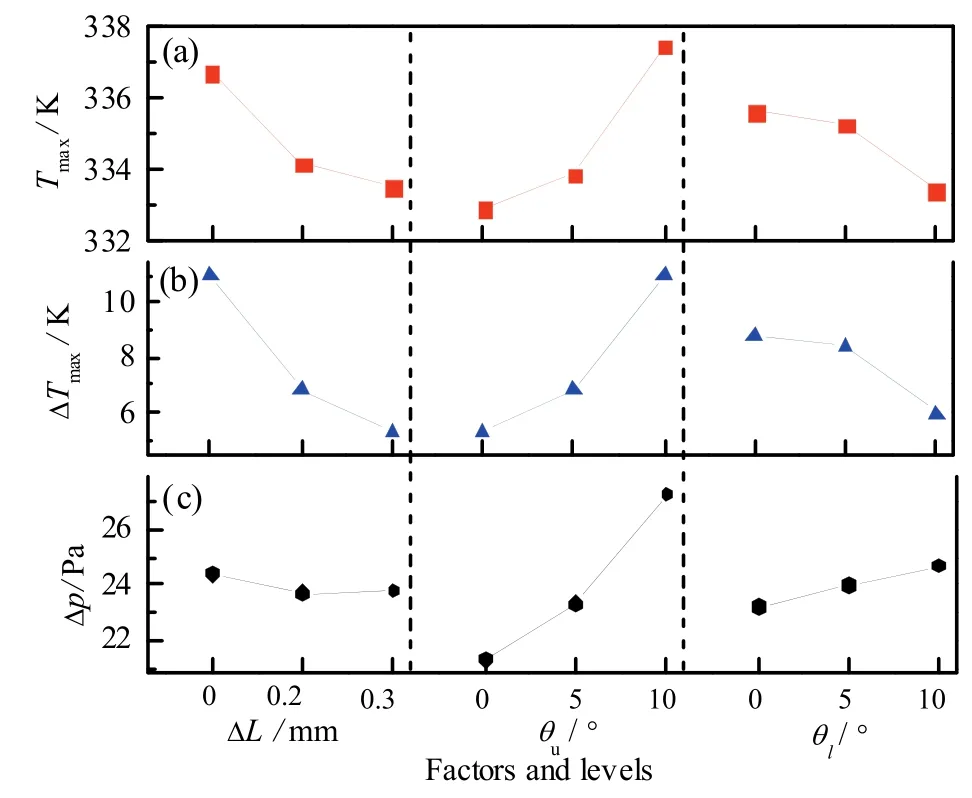
图2 Tmax、ΔTmax和Δp的平均值Fig. 2 Average of Tmax，ΔTmaxand Δp for each factor

2.1 各因素对温度场、压力场的影响

由图2可知，ΔL值的上升会导致 Tmax、ΔTmax的显著下降，但对Δp影响较小。这是由于，ΔL的上升增加了空气上游流道截面积、减小了空气下游流道截面积，有助于平衡各流道内空气的流量，能够有效抑制最高温度和模块间的温差［9］。如图 3所示，ΔL=0.3 mm时，各流道内工质流量更为均匀。

上集流板倾斜角度 θu值的增加会导致 Tmax、ΔTmax和Δp的上升，且影响较大。这是由于集流板倾斜角度越小，冷却空气在电池组内的阻力越大，增加了湍流程度，有助于提高换热系数，降低电池组内最高温度，同时平衡了各流道出口处的压强，如图4所示。

图3 不同ΔL下的流道内工质体积流量Fig. 3 Volume flow of working medium in each flow channel under different ΔL

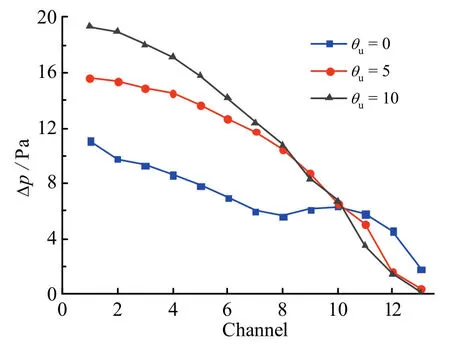
图4 不同θu下的流道进出口压差Fig. 4 Pressure drop of each flow channel under different θu

下集流板倾斜角度 θl的增大会导致 Tmax和ΔTmax下降，图5显示θl的增大有效提高了下游流道入口处的风速，平均流速的上升有利于增大换热系数，提高换热效率。但较高的风速也会增大湍流程度，从而增大Δp，如图2c所示。

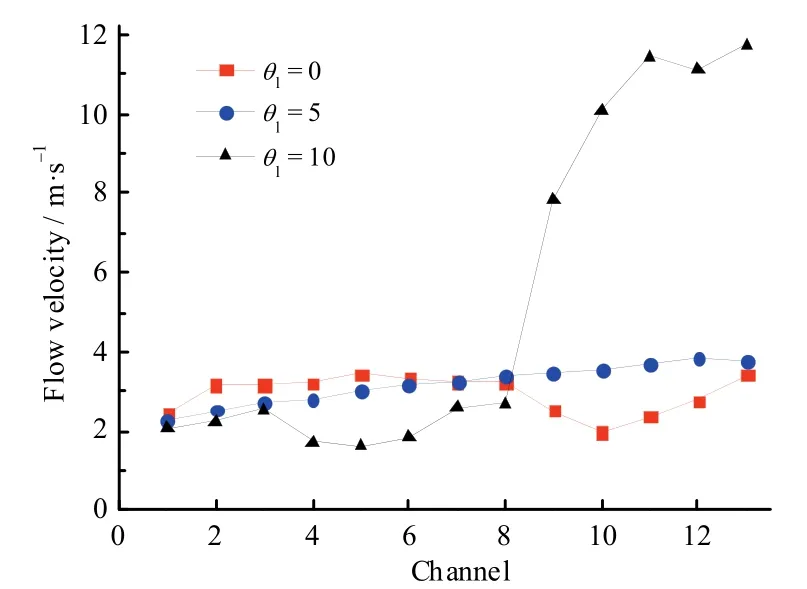
图5 不同θl下的流道入口风速Fig. 5 Inlet velocity of each flow channel under different θl

2.2 最优结构筛选

2.2.1 以Tmax为指标

表4中Rθu＞RΔL＞Rθl，因此θu的水平对试验结果影响最大，应优先考虑，ΔL次之，θl再次之。

对于θu，k1＜k2＜k3，说明θu的增大会提升最高温度Tmax，因此水平I最优。对于ΔL，k1＞k2＞k3，说明随着间距递减值的增大，最高温度下降，水平III最优。对于θl，k1＞k2＞k3，说明下集流板倾斜角度θl的增大有利于抑制最高温度Tmax，水平III最优。

因此，以最高温度 Tmax为指标，表 3中 No.7（AIIIBICIII）是最优组合，其最高温度Tmax最小。

2.2.2 以ΔTmax为指标

表4中Rθu＞RΔL＞Rθl，即θu的水平变化对温度的均匀性影响最大。

与最高温度Tmax的情况相似，θu的增大、θl的增大、ΔL的减小，都可以减小ΔTmax的值，即有助于提高电池组温度分布的均匀性。因此，以最高温度差ΔTmax为指标。表3中No.7（AIIIBICIII）是最优组合，电池组均匀性最好，其最高温度差ΔTmax最小。

2.2.3 以Δp为指标

表4中Rθu＞Rθl＞RΔL，这表明ΔL的水平变动对进出口压力差影响最小。随着θu和θl的增大，进出口压力差Δp均呈上升趋势。

因此，为降低电池组的最高温度 Tmax、降低模块间最大温差ΔTmax，应采用较大的ΔL、θl和较小的θu，表3中No.7（AIIIBICIII）是最优组合，其最高温度Tmax、最高温度差ΔTmax最小。

当以进出口压力差Δp为指标时，最优结构参数组合为AIIBICI（ΔL=0.2 mm，θu=0°，θl=0°）。由于该组合不在表3中，另对该结构仿真计算：Tmax=332.7 K，ΔTmax=5.2 K，Δp=20.4 Pa。进出口压力差 Δp确实略低于表 3的所有结果，但该结构ΔTmax＞5 K，温度均匀性较差，No.7（AIIIBICIII）仍为最优结构。

2.3 进一步优化

由2.1节分析可知：较小的θu和较大的θl有利于降低电池组的最高温度、提高温度场均匀性。为了进一步探讨θu和θl的影响规律，另作因素设置，如表 5。同样方法做正交实验设计，仿真计算。各因素对评价指标的影响趋势如图6所示。

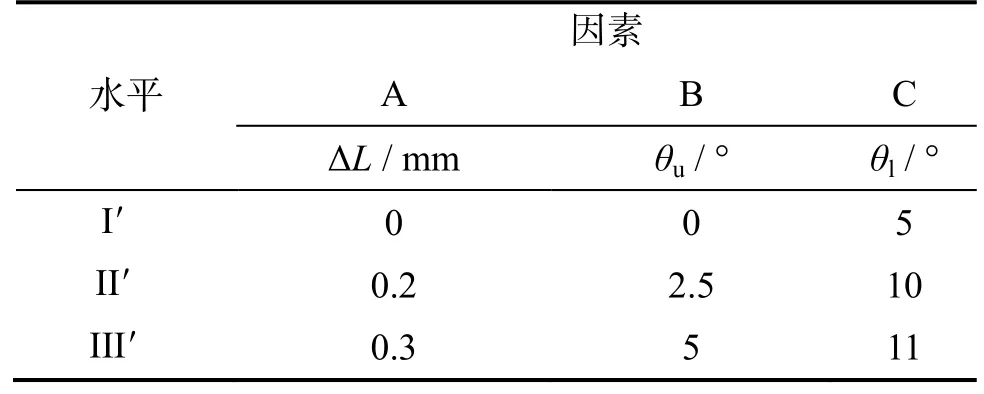
表5 因素水平表Table 5 Factors and levels of orthogonal experiment

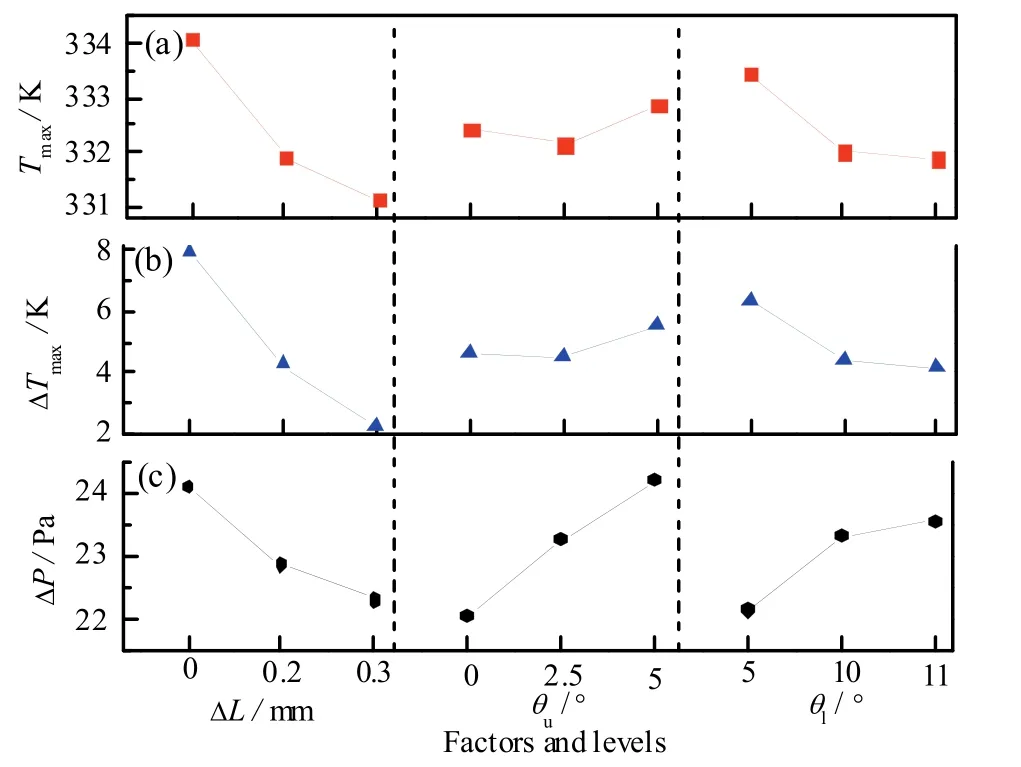
图6 Tmax、ΔTmax和Δp的平均值Fig. 6 Average of Tmax，ΔTmaxand Δp for each factor

图6 a中ΔL的水平改变对Tmax影响最大，作用规律与图2一致，水平III′最优。θl的减小仍显示了对降低 Tmax的有利影响，水平 III′最优。θu的增加会导致Tmax先减小后增大，这种影响较小，水平II′最优。

图6b中ΔL、θu、θl三个因素分别对ΔTmax的作用规律与对Tmax的作用规律一致。

图6c中ΔL的增大会降低进出口压力差Δp，水平III′最优。而θu、θl均为水平I′最优。

综上分析，得到基于温度的最优结构X和基于压力的最优结构Y：

结构X：ΔL=0.3 mm，θu=2.5°，θl=11°；

结构Y：ΔL=0.3 mm，θu=0°，θl=5°。

对结构X、Y建模计算，除了ΔL、θu、θl外，其他设置均不变，结果见表6。

表6 结构X、Y仿真结果Table 6 Simulation results of structure X and Y

结构 X的 Tmax、ΔTmax分别比表 3中 No.7（AIIIBICIII）降低了0.1 K、0.12 K，降幅较小，但Δp上升了1.2 Pa。由图6可知，θu的变化、θl由10°增加到11°对Tmax、ΔTmax影响均较小，但θu和θl的增大引起了Δp较大的增长。

与表3中No.7（AIIIBICIII）相比，结构Y的Tmax和 ΔTmax虽有所上升，但最高温度和电池组温度均匀性可以满足要求，同时Δp下降到了20.6 Pa，能耗最低。

综上分析，结构Y为最优结构，即：间距递减幅度0.3 mm，上集流板倾斜0°，下集流板倾斜5°。对最优结构的电池组进行2 C放电稳态仿真计算，图7给出了对称面温度云图。

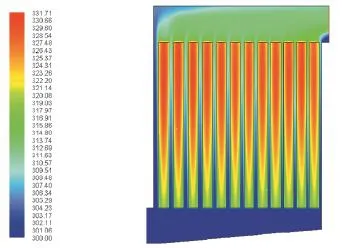
图7 电池组对称面温度云图Fig. 7 Temperature field cloud picture of battery pack symmetry plane

3 电池组放电仿真与实验对比

电池模块由空气入口附近往后依次编号1～12。电池组分别采用0.5 C、1 C、2 C倍率放电，生热速率如表1所示，冷却风速分别采用1 m·s-1、1.2 m·s-1和3 m·s-1。实验中电池组的测温点与数值模拟的取温点位置相同，选取各电池模块靠近空气入口侧的表面的中心点。

仿真结果显示，放电结束时，各电池模块表面中心温度的仿真值与实验值的趋势一致，如图8所示，各电池模块表面温度均匀性较好。

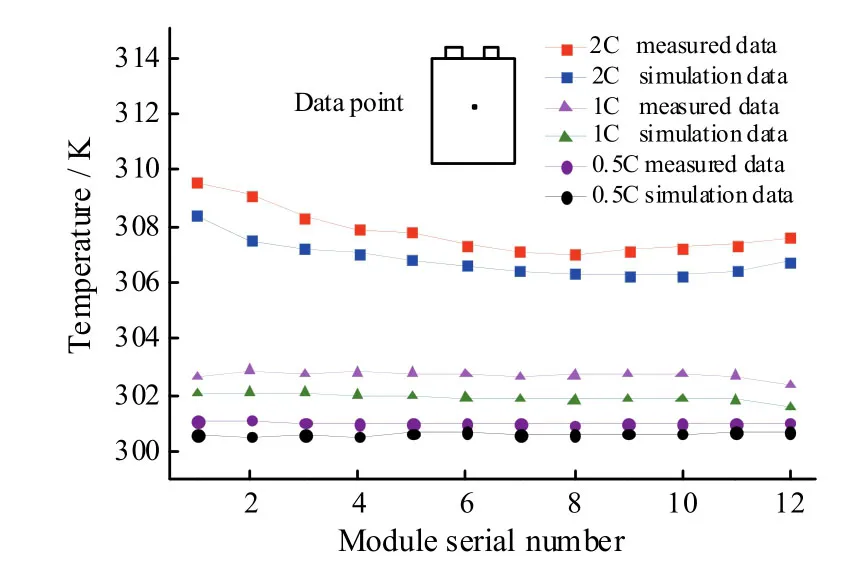
图8 放电结束时各电池模块表面中心温度Fig. 8 Surface center temperature of each battery module at the end of discharge

2 C放电结束时，电池组内模块最高温度为312.36 K，在锂离子电池最佳工作温度范围；不同模块最高温度最大相差0.95 K，能满足电池组温度一致性要求。

图9显示了放电过程中模块2的表面中心温度变化曲线，仿真与实验结果基本吻合。在放电初期，实验值低于仿真值，后期实验值较高，主要是由于仿真过程未考虑电池生热速率变化对电池温度分布的影响［10］。恒倍率放电时电池各区域生热速率不断变化，放电前期电极附近区域生热速率大于其他区域；放电后期电极远端区域生热速率最大［11］。整个电池模块前期生热速率较小，后期由于温度的上升引起内阻增大，不可逆热增加，生热速率不断上升。放电结束后，电池温度仍会继续上升一段时间。

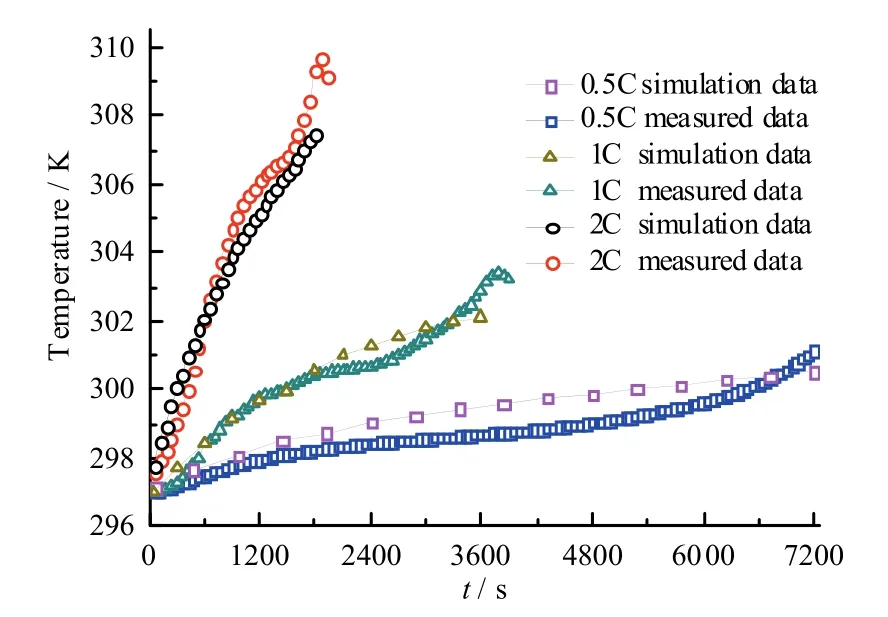
图9 放电过程中模块2的表面中心温度变化曲线Fig. 9 Surface center temperature of module 2 in the process of discharge

4 总 结

运用正交试验法设计电池组散热结构参数优化试验方案，研究电池组间距递减幅度、上下集流板倾斜角度变化。电池组间距递减幅度的增大有利于抑制电池组的温升、提高温度均匀性，同时有利于降低进出口压差；上集流板倾斜角度的增大不利于控制温度场、进出口压差；增大下集流板倾斜角度对控制温度场有利，但会提高进出口压差。综合温度场、进出口压差因素，确定了电池组最优结构参数：间距以0.3 mm递减，上集流板倾斜0°，下集流板倾斜5°。

根据优化结构，实验研究和仿真了0.5 C、1 C、2 C恒倍率放电工况下电池组的温度变化，结果基本吻合，电池组最高温度在最佳工作范围内，温度均匀性较好。研究中还存在一些不足：没有考虑锂离子电池热物性的温度依赖性；采用均一化电池生热模型，未考虑不同区域生热速率随时间变化的影响。这些都有待进一步研究。

［1］ PALACÍN M R，DE GUIBERT A. Why do batteries fail？［J］. Science，2016，351（6273）: 1253292. DOI: 10.1126/science.1253292.

［2］ PARK H. A design of air flow configuration for cooling lithium ion battery in hybrid electric vehicles［J］. Journal of power sources，2013，239: 30-36. DOI: 10.1016/ j.jpowsour.2013.03.102.

［3］ 赵佳腾，饶中浩，刘新健，等. 大功率锂离子动力电池组散热特性数值模拟［J］. 新能源进展，2014，2（6）: 471-475. DOI: 10.3969/j.issn.2095-560X.2014.06.010.

［4］ 孙秋娟，王青松，平平，等. 循环充放电条件下锂离子电池的温度模拟［J］. 新能源进展，2014，2（4）: 315-321. DOI: 10.3969/j.issn.2095-560X.2014.04.0012.

［5］ 白帆飞，宋文吉，陈明彪，等. 锂离子电池组热管理系统研究现状［J］. 电池，2016，46（3）: 168-171.

［6］ CHO G Y，CHOI J W，PARK J H，et al. Transient modeling and validation of lithium ion battery pack with air cooled thermal management system for electric vehicles［J］. International journal of automotive technology，2014，15（5）: 795-803. DOI: 10.1007/s12239-014-0083-x.

［7］ 刘瑞江，张业旺，闻崇炜，等. 正交试验设计和分析方法研究［J］. 实验技术与管理，2010，27（9）: 52-55. DOI: 10.3969/j.issn.1002-4956.2010.09.016.

［8］ LIU Y P，OUYANG C Z，JIANG Q B，et al. Design and parametric optimization of thermal management of lithium-ion battery module with reciprocating air-flow［J］. Journal of central south university，2015，22（10）: 3970-3976. DOI: 10.1007/s11771-015-2941-8.

［9］ GIULIANO M R，PRASAD A K，ADVANI S G. Experimental study of an air-cooled thermal management system for high capacity lithium-titanate batteries［J］. Journal of power sources，2012，216: 345-352. DOI: 10.1016/j.jpowsour.2012.05.074.

［10］ 罗玲，宋文吉，林仕立，等. 锂离子电池热模型的研究现状［J］. 电池，2015，45（5）: 280-283. DOI: 10.3969/j.issn. 1001-1579.2015.05.013.

［11］ XU M，ZHANG Z Q，WANG X，et al. A pseudo threedimensional electrochemical-thermal model of a prismatic LiFePO4battery during discharge process［J］. Energy，2015，80: 303-317. DOI: 10.1016/j.energy.2014.11.073.

Design and Optimization of Air-Cooled Structure for Lithium-Ion Battery Pack

BAI Fan-fei1，2，3，4，CHEN Ming-biao1，2，3，SONG Wen-ji1，2，3，FENG Zi-ping1，2，3
（1. Guangzhou Institute of Energy Conversion，Chinese Academy of Sciences，Guangzhou 510640，China；2. Key Laboratory of Renewable Energy，Chinese Academy of Sciences，Guangzhou 510640，China；3. Guangdong Provincial Key Laboratory of New and Renewable Energy Research and Development，Guangzhou 510640，China；4. University of Chinese Academy of Sciences，Beijing 100049，China）

Optimizing scheme of the air-cooled battery pack structure was designed by using the orthogonal test. The effects of the battery pack’s space decline range and the inclination angles of upper and lower deflectors on its temperature field，flow field and pressure drop were studied numerically. The optimal structure of the battery pack was determined: the space decline range is 0.3 mm，the angle of the upper deflector of 0° and the angle of the lower deflector is 5°. Temperature characteristics of the battery pack of such optimal structure were then investigated experimentally and numerically at discharging rates of 0.5 C，1 C and 2 C，respectively. The results show that both the maximum temperature and the temperature field uniformity of the battery pack can meet the requirements.

lithium-ion battery；air-cooled structure；orthogonal experiment；numerical simulation

TK02；TM912.2

A

10.3969/j.issn.2095-560X.2016.05.004

2095-560X（2016）05-0358-06

白帆飞（1989-），男，硕士研究生，主要从事储电系统热管理控制研究。

陈明彪（1985-），男，助理研究员，主要从事大规模储电系统及其控制技术研究。

宋文吉（1978-），男，博士，副研究员，主要从事大规模储电系统及其控制技术研究。

冯自平（1968-），男，博士，研究员，博士生导师，主要从事先进储能技术研究。

2016-05-12

2016-06-11

广东省科技计划项目（2014B010128001，2015B050501008）；广州市科技计划项目（201509010018）；中国科学院广州能源研究所重点实验室基金（Y607ji1001）

† 通信作者：宋文吉，E-mail：songwj@ms.giec.ac.cn