预设性能控制研究进展

胡云安，张　雷，耿宝亮

（海军航空工程学院控制工程系，山东烟台264001）

预设性能控制研究进展

胡云安，张雷，耿宝亮

（海军航空工程学院控制工程系，山东烟台264001）

介绍了预设性能控制的发展历程及研究现状，以具有一般形式的单输入单输出严格反馈非线性系统为例，阐述了性能函数和误差变换的概念，分析了预设性能控制的基本原理。通过其应用实例说明，预设性能控制能够解决工业生产、飞行器控制中的一些关键技术问题，因而有必要对预设性能控制方法进行深入研究。

预设性能控制；性能函数；误差变换

目前，非线性控制领域的研究成果均侧重于满足系统的稳态性能，而对系统的瞬态性能（包括超调量和收敛速度）则关注较少。然而，随着科技发展的日新月异，控制对象结构越来越复杂，而且要求精度高、实时性强，现有控制方法在提高控制性能方面的研究还相对比较匮乏，正是在此背景之下，预设性能控制应运而生，为解决性能控制问题提供了一种新的视角和研究思路，引起了控制界的广泛关注。预设性能控制[1]是希腊Bechlioulis等学者于2008年首次提出的一种新的控制方法。所谓预设性能是指在保证跟踪误差收敛到一个预先设定的任意小的区域的同时，保证收敛速度及超调量满足预先设定的条件，它要求瞬态性能和稳态性能的同时满足，直接以提高系统性能为目标。对于系统的控制性能问题，Miller[2]早在1991年就针对一类线性系统设计了具有非减动态增益的分段常值切换方法，保证跟踪误差在规定时间内收敛到预定的值。随后，Ryan等人针对一类非线性系统讨论了控制性能问题[3]，控制目标为：①跟踪误差收敛到一个半径为设定常值的区域内；②系统动态曲线在一个预先设定的性能通道内运行，这与预设性能控制的目标非常相似。

本文在已有文献的基础上分析了预设性能控制的基本原理，介绍了预设性能控制的理论和应用研究进展，通过其应用实例说明预设性能控制具有重要的研究意义。

1　预设性能控制基本原理

无论是单输入单输出非线性系统，还是多输入多输出非线性系统，预设性能控制都是围绕性能函数和误差变换这2个基本环节展开构建等效模型，再对等效模型进行控制器设计。下面，以具有一般形式的单输入单输出严格反馈非线性系统为例，引入性能函数和误差变换的概念，阐述预设性能控制的基本原理。

1.1系统描述

考虑具有一般形式的严格反馈非线性系统：

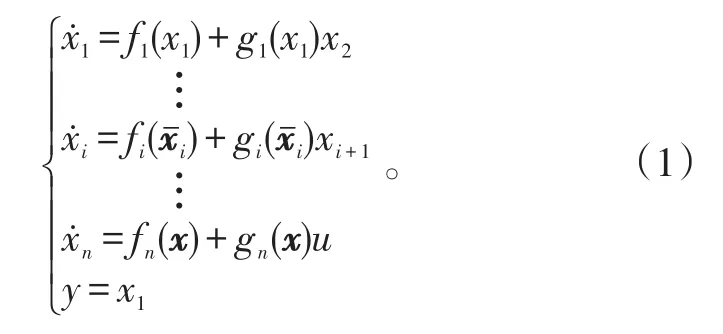
式（1）中：χ=[x1,x2,…,xn]T∈ℝn为系统的状态量，u∈ℝ和 y∈ℝ分别为系统的输入量和输出量；定义i=[x1,x2,…,xi]T∈ℝi；fi(⋅)、gi(⋅)为已知的连续光滑函数，设期望输出为yd(t)。

控制目标如下：

1）设计控制器u，保证输出误差e=y-yd满足预先设定的瞬态和稳态性能要求；

2）闭环系统中的所有信号保持有界。

1.2性能函数

通过引入性能函数，对跟踪误差e(t)的瞬态和稳态性能进行设定，性能函数的定义如下。

定义1：连续函数ϖ:ℝ+→ℝ+称为性能函数，如果满足：

1）ϖ(t)是正的且严格递减；

2）limt→∞ϖ(t)=ϖ∞＞0。

在初始误差e(0)已知的前提下，给出如下形式的不等式约束：

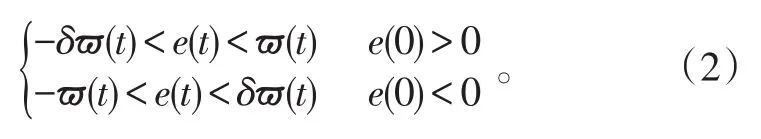
式（2）中：t∈[0,∞)；δ∈[0,1]。

当不等式（2）满足时，以e(0)＞0为例，则误差曲线将被限制在ϖ(t)和-δϖ(t)所包围的区域之中，另外，结合函数ϖ(t)的递减特性及δ∈[0,1]可知，误差e(t)将在函数ϖ(t)和-δϖ(t)的共同作用下迅速收敛到0的一个小邻域内，上述过程可借助图1～2进行说明。常数ϖ∞表示预先设定的稳态误差的上界，ϖ(t)的衰减速度为跟踪误差e(t)收敛速度的下界，同时跟踪误差的最大超调不会大于δϖ(0)。因此，通过选择适当的性能函数ϖ(t)和常数δ便可对输出误差的稳态和瞬态性能进行限制。

图1　跟踪误差与性能函数关系示意图（e(0)＞0）Fig.1 Schematic diagram of tracking error and performance function relationship（e(0)＞0）

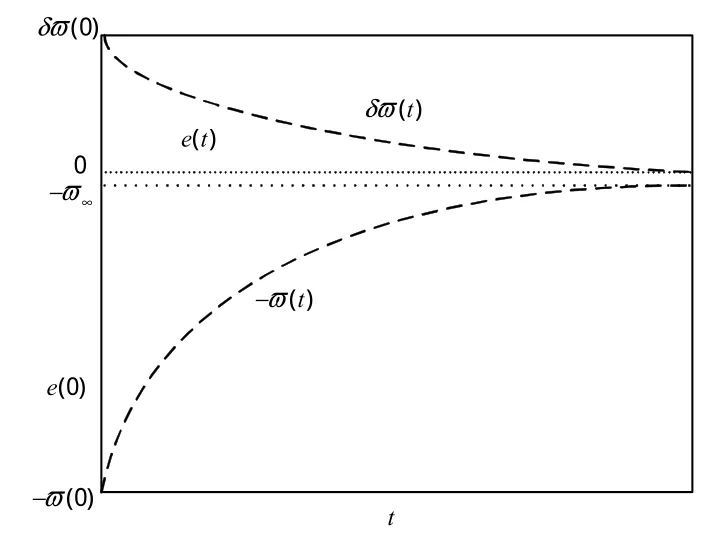
图2　跟踪误差与性能函数关系示意图（e(0)＜0）Fig.2 Schematic diagram of tracking error and performance function relationship（e(0)＜0）

1.3误差变换

在控制器设计过程中，直接对不等式约束（2）进行处理的难度非常大。因此，考虑先将不等式约束变换为等式约束，再对转换后的等效系统进行处理。定义误差变换函数 ftr(⋅)为

式（3）中：ε为变换误差；ftr(ε)满足以下条件：

ftr(ε)光滑且严格递增；

由上述定义可知，当e(0)＞0时，有-δ＜ftr(ε)＜1。

由定义1可知ϖ(t)＞0，则进一步有-δϖ(t)＜ϖ(t)ftr(ε)＜ϖ(t)

结合式（2）得到：-δϖ(t)＜e(t)＜ϖ(t)。同理，当e(0)＜0时，有-ϖ(t)＜e(t)＜δϖ(t)。因此，不等式约束（2）成立。

函数 ftr的逆变换为

显然，如果能够满足ε(t)∈ℓ∞（∀t∈[0,∞)），则可以推出不等式约束（2）成立，进一步可以保证跟踪信号满足预设性能的要求。

上述推导过程是在假设e(0)已知的前提下进行的，在很多情况下，这种假设是不合理的，当针对某些系统进行控制器设计时，事先往往不能得到初始误差的精确值。为了应对这一问题，文献[4]提出了一种不依赖于初始误差e(0)的变参数约束方案，消除了要求初始误差已知的限制。

1.4模型构建

选取满足式（2）、（3）型的性能函数和误差变换函数进行模型重构，对式（4）两边同时对时间求一阶导数，可以得到：

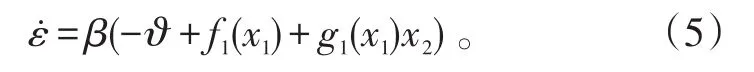
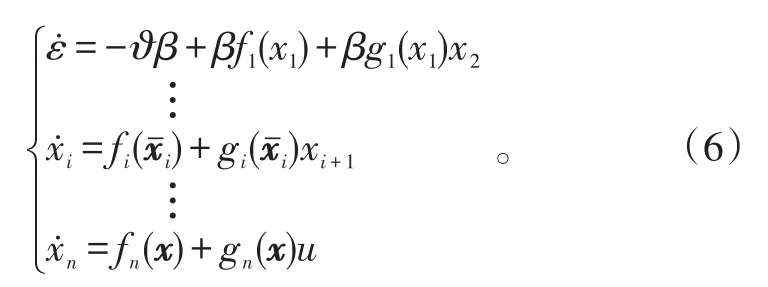
考虑系统（1），其目标函数满足性能函数（2），经变换函数（3）进行函数变换后得到系统（6），实现了将不等式约束变换为等式约束问题，设计控制器使当经函数变换后的系统（6）稳定时，系统（1）稳定且满足预设性能要求。

2　预设性能控制研究进展

近几年，随着非线性控制理论的巨大发展，越来越多的专家学者投入到预设性能控制的研究中，无论在其理论发展和应用研究都达到了空前的程度。文献[5]将预设性能控制的研究对象进一步推广到了多输入多输出反馈线性化系统，变换后的误差最终收敛且闭环系统内所有信号有界。文献[6]针对一类仿射多输入多输出非线性系统，采用控制Lyapunov函数、自适应技术完成了预设性能状态反馈控制器设计，并成功克服了在函数估计过程中可能出现的系统不可控问题。文献[7]针对具有未知非线性函数的串级系统完成了部分状态反馈控制器设计，保证系统跟踪误差满足预设性能，方法结构简单且仅需系统部分信息。文献[8-10]针对一类仅输出可测的非仿射非线性系统，完成了输出反馈控制器设计，保证系统的稳态和瞬态性能满足预设设定的要求，系统中的不确定项利用神经网络进行逼近，控制器设计采用了切换函数的形式。文献[11]在预设性能控制的基础上构建了一种新的方法，避免了复杂的神经网路紧集选择过程。文献[12]解决了一类带有死区的非线性系统的预设性能控制问题，将死区表示为时变函数的形式，利用Nussbaum函数解决了控制增益未知的问题，并提出了一种新的高阶神经网络对未知非线性进行逼近。文献[13-15]对具有严格反馈形式的非线性系统的预设性能控制问题进行了讨论，在一定假设的基础上初步解决了该类系统的控制性能问题。文献[16-18]将预设性能的概念与输出反馈相结合，提出了预设性能输出反馈控制器的设计方法。文献[19]将预设性能的概念应用到机械臂位置跟踪问题中，在保证跟踪误差收敛到一个预先设定的任意小的区域的同时，保证收敛速度及超调量满足预先设定的条件。文献[20]针对带输入死区、不确定项和扰动的严格反馈非线性系统设计了一种连续的、低复杂度的静态状态反馈预设性能控制器，摒弃了神经网络和模糊系统的引入，避免了反演控制方法存在“计算膨胀”问题，设计简单，为低复杂的预设性能控制器设计扩宽了思路。文献[21]针对一类包含非匹配不确定项、时变延迟、不可测状态的非线性大刻度系统提出了自适应模糊分散输出反馈预设性能控制器。利用模糊逻辑近似不确定项，利用模糊状态观测器估计不可测状态，利用“动态面”设计方法克服“计算膨胀”问题。最后，基于Lyapunov-Krasovskii理论证明系统闭环信号有界，跟踪信号满足性能要求。文献[22]针对一类包含输入饱和不可测状态的非线性随机系统提出了自适应模糊输出反馈预设性能控制器。利用模糊逻辑近似不确定项，输入饱和近似为光滑函数，利用模糊状态观测器估计不可测状态。文献[23]针对未知纯反馈系统进行普遍的、无近似状态反馈控制器设计，使在任何初始系统条件下，输出跟踪误差能满足预设性能且闭环系统全局收敛且有界。文献[24]针对内部关联的时滞系统设计输出反馈预设性能控制器，设计降阶观测器取代传统观测器在线估计不可测状态，提出新型的误差变换函数，利用反演控制方法进行设计。文献[25]针对单输入单输出非线性系统提出了一种神经网络学习机制，用新型转换函数将约束跟踪问题转换为某系统的稳定性问题，利用RBF神经网络近似滤波跟踪误差，利用自适应控制方法进行控制器设计，稳定神经网络控制可以获取并存储未知系统动态信息并用于在线控制，收敛速度快，计算负担小。

目前，预设性能控制的理论研究和应用主要集中在国外院校和学术团体，虽然已经引起了国外学者的广泛关注，在结构设计、稳定性分析以及性能改善等方面都有一定的研究，但是在国内鲜有团队[4，26-29]对其进行深入研究。文献[4]针对一类控制方向未知的不确定严格反馈非线性系统的预设性能自适应神经网络反演控制问题，提出了一种新的误差转化方法，放宽了对初始跟踪误差已知的限制，综合运用Nussbaum函数和反演控制技术设计了控制器。文献[26]针对一类严格反馈非线性系统，基于Lyapunov理论进行backstepping控制器的设计，并进行了稳定性分析。文献[27]针对一类控制增益为未知函数的不确定严格反馈系统，引入积分型Lyapunov函数，避免了因控制增益未知而引起的系统奇异问题，综合运用自适应技术、径向基函数神经网络和反演控制方法完成了控制器的设计，系统中的未知函数利用RBF神经网络直接进行逼近。文献[28]针对一类控制增益为未知常数严格反馈非线性系统的预设性能反演控制问题进行了研究，利用自适应估计器实现了对未知控制增益的逼近，并将虚拟控制量的跟踪问题转化为误差状态量的有界性问题，完成了反演控制器的设计。文献[29]针对一类具有外界扰动的严格反馈非线性系统，将Backstepping技术、预设性能控制和鲁棒控制相结合，提出一种预设性能鲁棒控制器设计方法。利用Backstepping和鲁棒控制逐步递推选择适当的Lyapunov函数设计预设性能鲁棒控制器。预设性能控制器设计方法多种多样，有代表性的控制方法为自适应控制方法[1-3，5-7]、输出反馈控制法[8-10]、状态反馈控制法[19-20]、模糊控制法[21-22]、神经网络法[4，26-27]、典型反演控制方法[28]、鲁棒控制方法[29]等，这里不再逐一介绍。

3　预设性能控制应用

在很多实际系统的控制过程中，对稳态性能和瞬态性能同时提出了很高的要求，而不是仅仅保证系统稳定。目前，预设性能控制已应用到了部分实际系统中，改善了系统的控制性能。文献[30-31]应用预设性能控制解决了具有参数不确定性的机械臂模型的力/位置跟踪控制问题。文献[32]进一步考虑机械臂模型中存在有界扰动的情况，利用鲁棒设计技巧保证了闭环系统的控制性能。文献[33]针对机械臂模型提出了一种不依赖于模型结构和参数的预设性能控制器设计方法，无需机械臂的动态模型信息和力变模型信息，取得了比较理想的控制效果。文献[34-35]将预设性能的概念与PID控制相结合，完成了机器人关节的速度和位置控制，保证速度和位置误差趋向于零的同时，超调量和收敛速度也满足了预先设定的要求。文献[36-37]将文献[7]的成果应用到了机械臂的力和位置跟踪过程中，均达到了预期的控制目标。另外，利用预设性能控制解决机械臂的实际控制问题还取得了许多其他成果[38-41]。文献[42]针对带非线性跳跃、线性阻尼动态的车辆主动悬挂系统设计了自适应预设性能控制器，使悬挂震动满足预设要求，提高了驾乘的舒适性。通过分析预设性能控制自身的特性和目前的典型应用可知，预设性能控制方法能够解决工业生产、飞行器控制中的一些关键技术问题，具有十分重要的工程实际意义[43]。

4　总结与展望

通过分析目前国内外研究者在预设性能控制研究中所取得的成果发现，在预设性能控制的研究领域中存在如下问题急待解决。

1）预设性能控制均有不严谨和不合理之处，具体可总结为：①缺乏统一严格的稳定性分析；②设计过程中用到了未知参数的猜测值，而这个猜测值本身是难以得到的；③控制量不够光滑。

2）已有的绝大部分文献仅针对严格反馈非线性系统和仿射非线性系统进行研究，可以考虑将模型进一步推广到多输入-多输出系统、非仿射非线性系统情况，以及更具一般形式的非线性系统，例如混沌系统，时变非线性系统等。

3）进一步拓宽应用对象，充分利用预设性能控制的优势解决军事、航空航天等众多领域的难点控制问题，体现其工程价值。

目前，非线性系统的预设性能控制问题的相关研究还处于起步阶段，尚未形成一套完整的理论体系，许多难点问题亟待解决，随着非线性控制理论的巨大发展，相信会有更多的国内外学者关注和从事这个富有挑战性的研究，使该领域的相关问题得到进一步的研究和解决。

[1]BECHLIOULIS C P，ROVITHAKIS G A.Prescribed performance adaptive control of SISO feedback linearizable systems with disturbances[C]//16thMediterranean Conference on Control&Automation（MED）.Ajaccio，France：IEEE，2008：1035-1040.

[2]MILLER D E，DAVISON E J.An adaptive controller which provides an arbitrarily good transient and steadystate response[J].IEEE Transactions on Automatic Control，1991，36（1）：68-81.

[3]RYAN E P，SANGWIN C J，TOWNSEND P.Controlled functional differential equations：approximate and exact asymptotic tracking with prescribed transient performance [J].ESAIM：Control，Optimisation&Calculus of Variations，2009，15（4）：745-762.

[4]耿宝亮，胡云安.控制方向未知的不确定系统预设性能自适应神经网络反演控制[J].控制理论与应用，2014，31（3）：397-403. GENG BAOLIANG，HU YUNAN.Prescribed performance adaptive neural backstepping control for nonlinear system with uncertainties and unknown control directions [J].Control Theory&Applications，2014，31（3）：397-403.（in Chinese）

[5]BECHLIOULIS C P，ROVITHAKIS G A.Robust adaptive control of feedback linearizable MIMO nonlinear systems with prescribed performance[J].IEEE Transactions onAutomatic Control，2008，53（9）：2090-2099.

[6]BECHLIOULIS C P，ROVITHAKIS G A.Prescribed performance adaptive control for multi-input multi-output affine in the control nonlinear systems[J].IEEE Transactions onAutomatic Control，2010，55（5）：1220-1226.

[7]BECHLIOULIS C P，ROVITHAKIS G A.Robust partialstate feedback prescribed performance control of cascade systems with unknown nonlinearities[J].IEEE Transactions onAutomatic Control，2011，56（9）：2224-2230.

[8]KOSTARIGKAA K，ROVITHAKIS G A.Prescribed performance output feedback control：an approximate passiv-ation approach[C]//18thMediterranean Conference on Control&Automation（MED）.Marrakech，Morocco：IEEE，2010：1483-1494.

[9]KOSTARIGKAA K，ROVITHAKIS G A.Prescribed performance output feedback/observer-free robust adaptive control of uncertain systems using neural networks[J]. IEEE Transactions on Systems，Man，and Cybernetics：Cybernetics，2011，41（6）：1483-1494.

[10]KOSTARIGKA A K，ROVITHAKIS G A.Adaptive dynamic output feedback neural network control of uncertain MIMO nonlinear systems with prescribed performance[J].IEEE Transactions on Neural Networks and Learning Systems，2012，23（1）：138-149.

[11]BECHLIOULIS C P，ROVITHAKIS G A.A priori guaranteed evolution within the neural network approximation set and robustness expansion via prescribed performance control[J].IEEE Transactions on Neural Networks and Learning Systems，2012，23（4）：669-675.

[12]NA J.Adaptive prescribed performance control of nonlinear systems with unknown dead zone[J].International Journal of Adaptive Control and Signal Processing，2013，27（5）：426-446.

[13]BECHLIOULIS C P，ROVITHAKIS G A.Approximation-free prescribed performance control for unknown SISO pure feedback systems[C]//Proceedings of European Control Conference（ECC）.Zurich，Switzerland：IEEE，2013：4544-4549.

[14]BECHLIOULIS C P，ROVITHAKIS G A.Adaptive control with guaranteed transient and steady state tracking error bounds for strict feedback systems[J].Automatica，2009，45（2）：532-538.

[15]BECHLIOULIS C P，ROVITHAKIS G A.Robust approximation free prescribed performance control[C]//19thMediterranean Conference on Control&Automation（MED）. Corfu，Greece：IEEE，2011：521-526.

[16]ARTEMIS K K，GEORGE A R.Prescribed performance output feedback control：an approximate passivation approach[C]//18thMediterranean Conference on Control& Automation（MED）.Marrakech，Morocco：IEEE，2010：11-16.

[17]ARTEMIS K K，GEORGE A R.Prescribed performance output feedback/observer-free robust adaptive control of uncertain systems using neural networks[J].IEEE Transactions on Systems，Man，and Cybernetics，2011，41（6）：1483-1494.

[18]ARTEMIS K K，GEORGE A R.Adaptive dynamic output feedback neural network control of uncertain MIMO nonlinear systems with prescribed performance[J].IEEE Transactions on Neural Networks and Learning Systems，2012，23（1）：138-149.

[19]CHARALAMPOS P B，ZOE D，GEORGE A R.Robot force/position tracking with guaranteed prescribed performance[C]//IEEE Internalization Conference on Robotics andAutomation.Kobe：IEEE，2009：3688-3693.

[20]ACHILLES THEODORAKOPOULOS，GEORGE A. Guaranteeing preselected tracking quality for uncertain strict-feedback systems with deadzone input nonlinearity and disturbances via low-complexity control[J].Automatica，2015，54（2）：135-145.

[21]LI YONGMING，TONG SHAOCHENG.Prescribed performance adaptive fuzzy output-feedback dynamic surface control for nonlinear large-scale systems with time delays[J].Information Sciences，2015，292（3）：125-142.

[22]SUI SHUAI，TONG SHAOCHENG，LI YONGMING. Observer-based fuzzy adaptive prescribed performance tracking control for nonlinear stochastic systems with input saturation[J].Neurocomputing，2015，158（2）：100-108.

[23]CHARALAMPOS P BECHLIOULIS，GEORGE A ROVITHAKIS.A low-complexity global approximation-free control scheme with prescribed performance for unknown pure feedback systems[J].Automatica，2014，50（8）：1217-1226.

[24]HUAN CHANGCHUN，ZHANG LIULIU，GUAN XINPING.Output feedback control for interconnected timedelay systems with prescribed performance[J].Neurocomputing，2014，129（3）：208-215.

[25]WANG MIN，WANG CONG，LIU XIAOPING.Dynamic learning from adaptive neural control with predefined performance for a class of nonlinear systems[J].Information Sciences，2014，279（1）：874-888.

[26]胡云安，耿宝亮，赵永涛.严格反馈非线性系统预设性能backstepping控制器设计[J].控制与决策，2014，29（8）：1509-1512. HU YUNAN，GENG BAOLIANG，ZHAO YONGTAO. Prescribed performance backstepping control of strict feedback nonlinear systems[J].Control and Decision，2014，29（8）：1509-1512.（in Chinese）

[27]耿宝亮，胡云安，李静，等.控制增益为未知函数的不确定系统预设性能反演控制[J].自动化学报，2014，40（11）：2522-2529. GENG BAOLIANG，HU YUNAN，LI JING，et al.Prescribed performance backstepping control of uncertain systems with unknown control gains[J].Acta Automatica Sinica，2014，40（11）：2522-2529.（in Chinese）

[28]胡云安，耿宝亮，盖俊峰.初始误差未知的不确定系统预设性能反演控制[J].华中科技大学学报：自然科学版，2014，42（8）：43-47. HU YUNAN，GENG BAOLIANG，GAI JUNFENG.Prescribed performance backstepping control for uncertain systems with unknown initial errors[J].Journal of Huazhong University of Science and Technology：Natural Science Edition，2014，42（8）：43-47.（in Chinese）

[29]陈明，张士勇.基于Backstepping的非线性系统预设性能鲁棒控制器设计[J].控制与决策，2015，30（5）：877-881. CHEN MING，ZHANG SHIYONG.Prescribed performance robust controller design for nonlinear systems based on Backstepping[J].Control and Decision，2015，30（5）：877-881.（in Chinese）

[30]BECHLIOULIS C，DOULGERI Z，ROVITHAKIS G. Prescribed performance adaptive control for robot force/ position tracking[C]//International Symposium on Intelligent Control.Saint Petersburg：IEEE，2009：920-925.

[31]BECHLIOULIS C，DOULGERI Z，ROVITHAKIS G.Robot force/position tracking with guaranteed prescribed performance[C]//International Conference on Robotics andAutomation.Kobe，Japan：IEEE，2009：3688-3693.

[32]DOULGERI Z，KARAYIANNIDIS Y，ZOIDI O.Prescribed performance control for robot joint trajectory tracking under parametric and model uncertainties[C]// 17thMediterranean Conference on Control&Automation（MED）.Thessaloniki，Greece：IEEE，2009：1313-1318.

[33]BECHLIOULIS C，DOULGERI Z，ROVITHAKIS G. Model free force/position robot control with prescribed performance[C]//18thMediterranean Conference on Control&Automation（MED）.Marrakech，Morocco：IEEE，2010：377-382.

[34]DOULGERI Z，KARAYIANNIDIS Y.PID type robot joint position regulation with prescribed performance guaranties[C]//International Conference on Robotics and Automation（ICRA）.Anchorage，Alaska：IEEE，2010：4137-4142.

[35]DOULGERI Z，DROUKAS L.Robot task space PID type regulation with prescribed performance guaranties[C]// Proceedings of the Intelligent Robots and Systems（IROS）.Taipei：IEEE，2010：1644-1649.

[36]BECHLIOULIS C P，DOULGERI Z，ROVITHAKIS G A.Neuro-adaptive force/position control with prescribed performanceandguaranteedcontactmaintenance[J]. IEEE Transactions on Neural Networks，2010，21（12）：1857-1868.

[37]KARAYIANNIDIS Y，DOULGERI Z.Robot joint position tracking with an approximator-free prescribed performance controller[C]//19thMediterranean Conference on Control&Automation（MED）.Corfu，Greece：IEEE，2011：564-569.

[38]KARAYIANNIDIS Y，DOULGERI Z.Regressor-free robot joint position tracking with prescribed performance guarantees[C]//Proceedings of International Conference on Robotics and Biomimetics（ROBIO）.Phuket，Thailand：IEEE，2011：2312-2317.

[39]KOSTARIGKA A K，DOULGERI Z，ROVITHAKIS G A.Prescribed performance tracking for flexible joint robots with unknown dynamics and elasticity[C]//International Conference on Robotics and Automation（ICRA）. SaintPaul，Minnesota：IEEE，2012：5365-5370.

[40]BECHLIOULIS C P，DOULGERI Z，ROVITHAKIS G A.Guaranteeing prescribed performance and contact maintenance via an approximation free robot force/position controller[J].Automatica，2012，48（2）：360-365.

[41]KARAYIANNIDIS Y，DOULGERI Z.Model-free robot joint position regulation and tracking with prescribed performance guarantees[J].Robotics and Autonomous Systems，2012，60（2）：214-226.

[42]HUANG YINGBO，NAN JING，WU XING，et al.Adaptive control of nonlinear uncertain active suspension systems with prescribed performance[J].ISA Transactions，2015，54（10）：145-155.

[43]GAI W，WANG H，ZHANG J，et al.Adaptive neural network dynamic inversion with prescribed performance for aircraft flight control[J].Journal of Applied Mathematics，2013，45（12）：1-12.

Research Development of Prescribed Performance Control

HU Yunan,ZHANG Lei,GENG Baoliang
（Department of Control Engineering,NAAU,Yantai Shandong 264001,China）

The development and present research situation of prescribed performance control were reviewed.General form single-input single-output strict-feedback nonlinear system was used as example,fundamental principle was analyzed by introducing conceptions of performance function and error transformation.The existing research results showed that some critical technical problems in industry and aircraft control had been solved by prescribed performance control,therefore, prescribed performance control had further research prospects.

prescribed performance control;performance function;error transformation

TP273

A

1673-1522（2016）01-0001-06

10.7682/j.issn.1673-1522.2016.01.001

2015-11-16；

2015-12-29

国家自然科学基金资助项目（60674090）；中国博士后基金资助项目（2015M572693）

胡云安（1966-），男，教授，博士，博导。