可变网格高阶有限差分法逆时偏移研究
马光克,李洋森,孙万元,刘 峰,廖显锋
(中海石油(中国)有限公司湛江分公司,广东湛江524000)
可变网格高阶有限差分法逆时偏移研究
马光克,李洋森,孙万元,刘峰,廖显锋
(中海石油(中国)有限公司湛江分公司,广东湛江524000)
在高阶有限差分法逆时偏移成像过程中,成像精度和计算效率是一对矛盾体,特别是对于小尺度细微地质构造的刻画。为了能在精细刻画局部地质体结构的同时,保证逆时偏移的计算效率,采用多尺度可变网格有限差分算法求解一阶应力-速度声波方程,将可变网格有限差分算法引入到逆时偏移中,对传统常规逆时偏移算法进行了改进,并将可变网格步长倍数的变化范围推广至任意奇数倍,分析了可变网格对有限差分算法数值频散的影响。不同模型偏移成像试验结果表明,可变网格逆时偏移算法能在保证地下地质体成像精度的同时提高偏移效率,有利于局部构造特征的精细刻画。
逆时偏移;可变网格;交错网格;深度偏移成像
自1983年WHITEMORE[1]提出逆时偏移成像技术以来,逆时偏移受到越来越多学者的关注与重视。目前,关于逆时偏移的研究主要包括四个方面:①双程波动方程逆时延拓算法和成像条件的改进;②逆时偏移的有效存储;③偏移噪声的压制;④逆时偏移的高效性。在双程波动方程逆时延拓算法和成像条件改进方面,KARAZINCIR等[2],ETGEN等[3]通过优化外推网格或改进波场外推方法有效提高了计算效率。在逆时偏移数据存储方面,SYMES[4],CLAPP[5]分别提出Checkpointing方法和随机边界条件,以计算换存储的策略解决了逆时偏移存储量大的问题。在偏移噪声压制方面,BAYSAL等[6]、LIU等[7]和YOON等[8]分别用无反射成像、波场分离成像以及Poynting矢量成像等方法较好地压制了偏移成像噪声。在提高逆时偏移计算效率方面,学者们多以高性能计算机平台为依托实现逆时偏移的加速[9],以增加逆时偏移的经济有效性和实用性。
双程波动方程叠前逆时偏移主要通过高阶有限差分法求解波动方程实现偏移成像,具有成像精确、无倾角限制等优点,更适用于横向速度变化剧烈的复杂介质的偏移成像。吸收边界和数值频散是高阶有限差分算法不可避免的两个问题[10],利用完美匹配层吸收边界条件可以较好解决有限区域边界吸收问题,利用小尺度网格离散等手段可以抑制数值频散。对于复杂地下构造,特别是存在低速层时,一般需要采用小尺度网格对整个模型进行离散,以便在保证稳定性的同时有效地抑制有限差分的数值频散。但小尺度网格采样增加了巨大的计算量,对于逆时偏移原本就低的计算效率来说,无疑是雪上加霜。因此,设计出更合理的高阶有限差分算法势在必行。
高阶有限差分逆时偏移因计算量大受限于计算机技术的发展,改善逆时延拓算法成为众多学者研究的焦点之一。为了提高高阶有限差分数值模拟的计算效率,MOCZO[11]首先提出可变网格有限差分思想;JASTRAM等[12]进一步将其应用到弹性波正演模拟中,并在不同网格尺度过渡区域采用插值算法实现不同网格波场值的计算;WANG等[13]在提高大小尺度网格比的基础上实现了对粘弹介质的模拟,解决了地表低速区域有限差分算法数值模拟不稳定的问题。国内关于可变网格有限差分算法的研究起步较晚,李振春等[14]给出了可变网格有限差分算法的任意偶数阶精度差分近似公式及差分系数求取方法,避免了在过渡带区域大量的插值计算;孙成禹等[15]发展了一种新的更容易实现的二维波动方程纵向可变网格有限差分算法,避免了插值计算;黄超等[16]将变化的空间网格与变化的时间步长相结合,提出一种空间网格大小与时间步长均可任意变化的高阶有限差分数值模拟方法。
以上都是针对可变网格正演模拟方面的研究,在逆时偏移方面可变网格的研究相对较少。由于逆时延拓与正演模拟是正反两个过程,因此本文在可变网格正演模拟的基础上,基于声波方程一阶应力-速度方程交错网格有限差分逆时偏移算法,将可变网格有限差分算法引入到逆时偏移中,对传统常规逆时偏移算法进行改进,以实现局部构造的精细刻画。
1 技术方法
1.1常规网格逆时延拓算法
在地震勘探中,二维各向同性介质中的一阶应力-速度声波方程可表示为:
(1)

按照传统常规交错网格有限差分算法[17]对公式(1)进行差分离散,可以推导出一阶应力-速度声波方程逆时延拓的高阶差分格式:
(2)
(3)
(4)
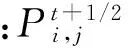
1.2可变网格逆时延拓算法
可变网格逆时延拓首先需要对速度(密度)场进行不同尺度网格的离散采样。图1给出了两种不同方式的速度场离散方案,方案一将全局速度场剖分为大小两种尺度的不同网格,在逆时延拓时需要对大小尺度网格边界点作插值处理;方案二则是在网格边界引入过渡区,避免了因插值计算引入的误差,可变网格逆时延拓算法也较容易实现。本文主要采用方案二中的离散方式进行分析计算。
根据常规交错网格逆时延拓的高阶差分格式,应力(或速度)分量仅与差分算子长度范围内的速度(或应力)分量有关。因此,在差分算子长度内若为相同尺度网格离散则均采用常规交错网格逆时延拓算法;反之则需采用新的差分算子进行高阶有限差分离散。图2给出了可变交错网格在过渡区的差分处理方式(为了保证大/小尺度网格过渡带的所有半节点导数不用插值就可以求出高阶差分数值,大/小尺度的网格步长比值需为奇整数倍,这里设大/小尺度网格步长比为l=3),L为大小尺度网格分界点。以∂vx/∂x速度分量(10阶差分精度)计算为例,高阶差分计算存在三种情况:①大尺度网格区域内部(0~L-5点);②小尺度网格区域内部(L+5~边界点);③大/小尺度网格过渡区域内部(L-5~L+5)。
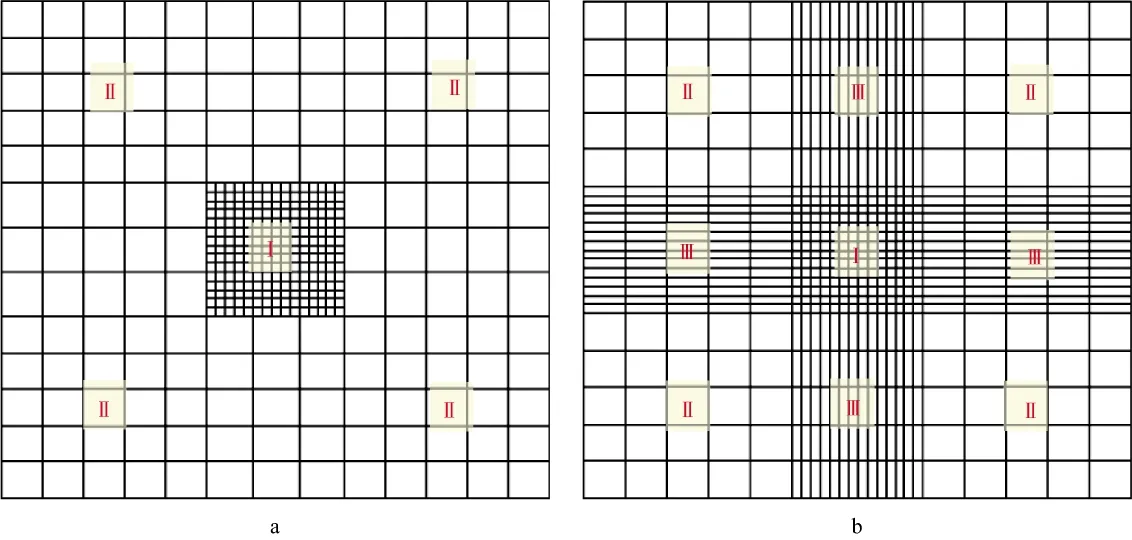
图1 速度(密度)场的离散方式a 方案一; b 方案二
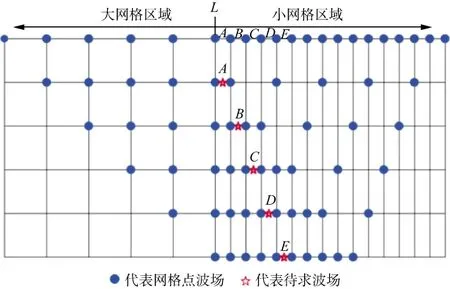
图2 可变交错网格差分算子在过渡区的处理方式
(5)
在小尺度网格区域内,一阶导数的高阶差分计算公式为:
(6)
而在大/小尺度网格过渡区域,需要重新计算网格差分系数,其一阶导数高阶差分计算公式可以表示为:
(7)
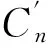
(8)
1.3可变网格逆时偏移成像条件
可变网格逆时偏移成像条件与常规网格逆时偏移成像条件算法类似,而逆时偏移低频噪声严重影响构造成像精度。前人针对逆时偏移低频噪声的去除方法主要分两类:一是滤波类[18],如高通滤波,Laplace滤波和最小平方滤波等;二是传播方向成像改进[19],如Poynting矢量互相关成像、波场分离互相关成像等。由于波场分离互相关条件能够在保证构造成像精度的同时较好地压制低频噪声,本文主要采用基于Poynting矢量波场分离的成像方法[20]分离出上、下、左、右行波,再对上、下、左、右行波分别进行成像。其归一化波场分离互相关条件可表示为:
(9)
式中:Su(x,z,t)和Ru(x,z,t)分别为炮、检点上行波;Sd(x,z,t)和Rd(x,z,t)分别为炮、检点下行波;Sl(x,z,t)和Rl(x,z,t)分别为炮、检点左行波;Sr(x,z,t)和Rr(x,z,t)分别为炮、检点右行波。
1.4可变网格逆时偏移数值频散分析
高阶有限差分算法用离散方程代替连续波动方程,单个波长内采样不足会不可避免地产生数值频散现象[21]。图3给出了2阶、4阶、6阶空间差分精度时不同纵横网格步长比数值频散的变化曲线,其中v为离散介质地震波相速度,v0为无频散时实际相速度。为了定量分析空间差分频散,这里引入最佳入射角(即空间差分数值频散最小时的入射角,如图3d中虚线所示)的概念,当入射角小于最佳入射角时,不同尺度网格的数值频散影响均较弱,而当入射角超过最佳入射角时,随着纵横网格步长比的增大,数值频散越来越严重。因此大纵横网格步长比可变网格算法不得不考虑数值频散的影响,可通过适当提高差分精度来抑制。
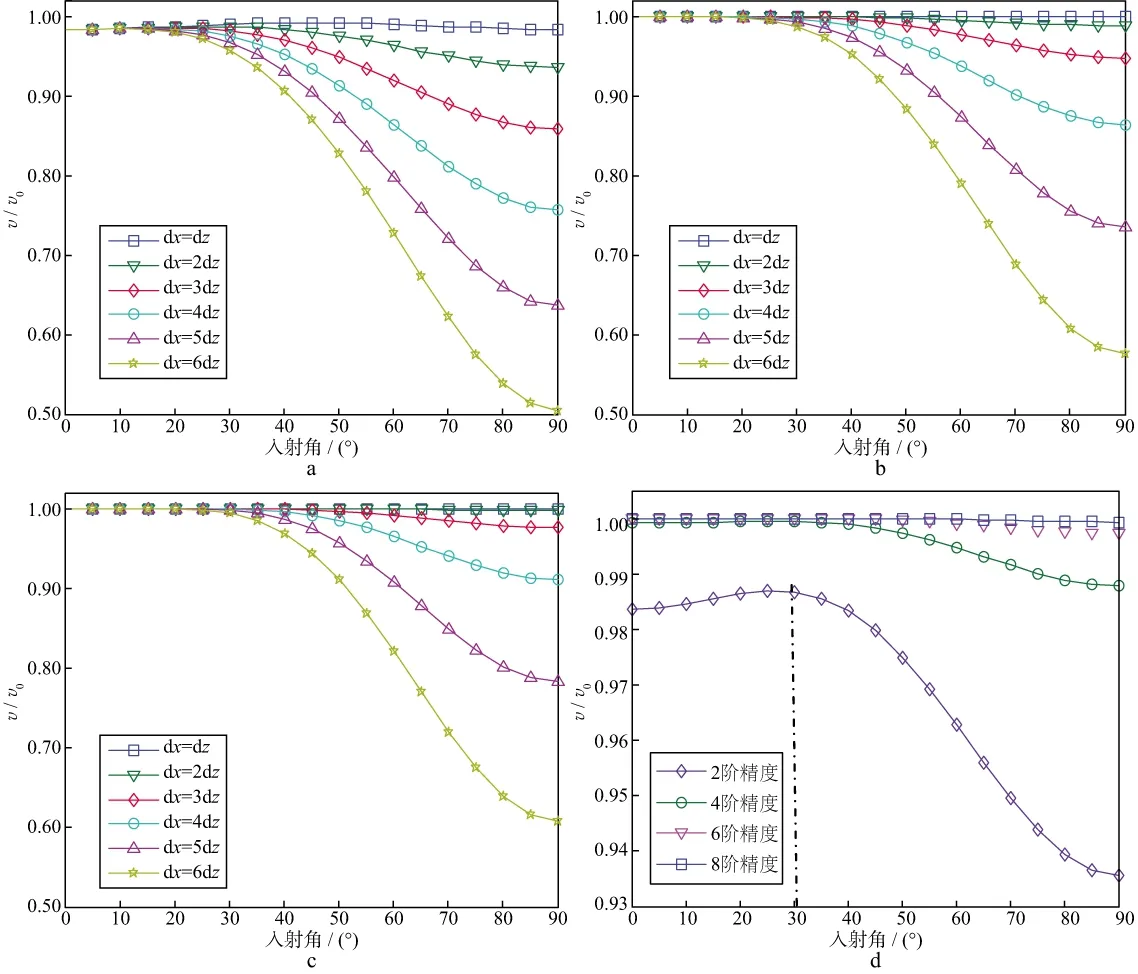
图3 不同尺度网格步长比数值频散变化曲线a 2阶; b 4阶; c 6阶; d dx=2dz
图4显示了不同速度和差分算子长度对差分数值频散的影响。在实际地震勘探中经常会遇到低速透镜体和高速侵入体的情况,低速透镜体要求差分算子长度长而高速侵入体要求差分算子长度短,若采用固定差分算子长度势必增加逆时延拓的计算量。多尺度可变网格逆时偏移算法在低速透镜体进行小尺度网格步长离散,对于相同差分精度在低速透镜体内的数值频散会有进一步的抑制,同时能提高逆时延拓的计算效率。

图4 不同速度和差分算子长度的计算误差
2 模型试验
可变网格逆时偏移算法在大/小尺度网格边界设置过渡区域,避免了插值因素影响,提高了数值模拟的计算效率。本文设计3种不同的介质模型来测试可变网格逆时偏移算法的有效性。
2.1双层水平介质模型
模型一为双层水平介质模型(图5),分别采用可变网格和传统网格逆时偏移算法进行偏移成像效果对比。可变网格逆时偏移在黄色虚线区域内的网格大小为2m×2m,其它区域(除过渡带外)的网格大小为6m×6m,时间采样步长为0.25ms;传统网格逆时偏移方法粗网格大小为6m×6m,时间采样步长为0.50ms,细网格大小为2m×2m,时间采样步长为0.25ms。炮点坐标均为(900m,6m),采用双边接收的方式。

图5 双层水平介质模型
由于不同尺度网格采用相同比例尺显示会造成波场快照(或偏移成像剖面)的拉伸或收缩,我们按照大尺度网格步长对小尺度网格进行重新采样,消除了不同尺度网格显示畸变的影响,得到校正后波场快照。图6为不同时刻可变网格正演模拟与逆时延拓波场快照,图7为可变网格与传统网格逆时偏移方法的单炮逆时偏移剖面,无论是从波场快照还是从逆时偏移剖面看,在大/小尺度网格边界都没有产生人为的异常反射。
2.2含孔洞介质模型
模型二为含孔洞介质模型(图8),分别采用可变网格和传统网格逆时偏移算法进行偏移成像对比。空间网格步长和时间网格步长均与模型一相同,只是模型二采用多炮偏移叠加方式。图9为两种网格类型多炮逆时偏移成像结果。在逆时偏移精度方面,可变网格和传统细网格逆时偏移对3种不同半径的孔洞均能精细成像,而传统粗网格逆时偏移由于采样方面的原因对半径R=2m的孔洞不能有效精确成像。在偏移成像时效方面,传统细网格逆时偏移计算时间是传统粗网格逆时偏移计算时间的17.67倍,而可变网格相对于传统细网格逆时偏移的计算效率提高了82.5%(表1)。因此,采用可变网格逆时偏移算法能在保证成像效率的同时,对局部构造特征进行精细刻画。
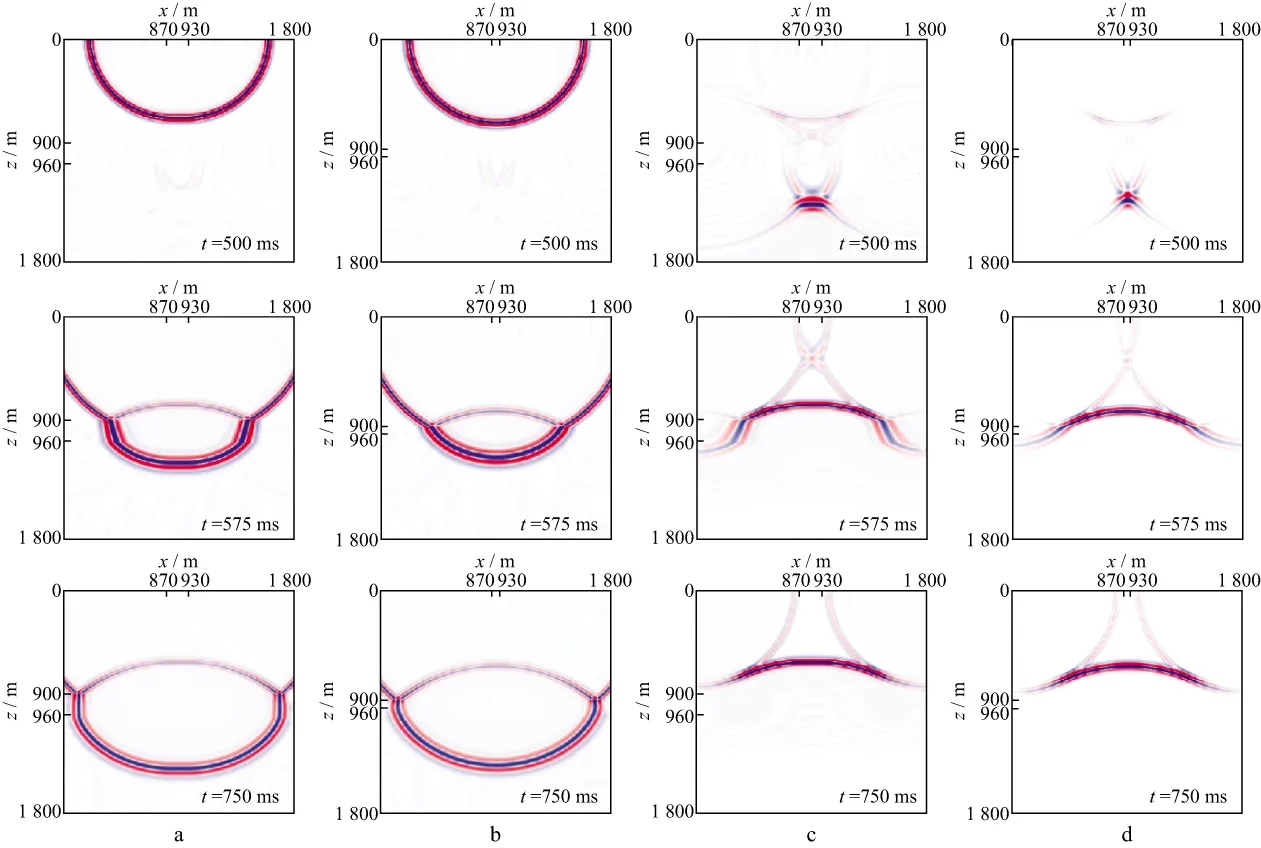
图6 可变网格有限差分正演模拟与逆时延拓波场快照a 正演模拟波场快照; b 校正后正演模拟波场快照; c 逆时延拓波场快照; d 校正后逆时延拓波场快照
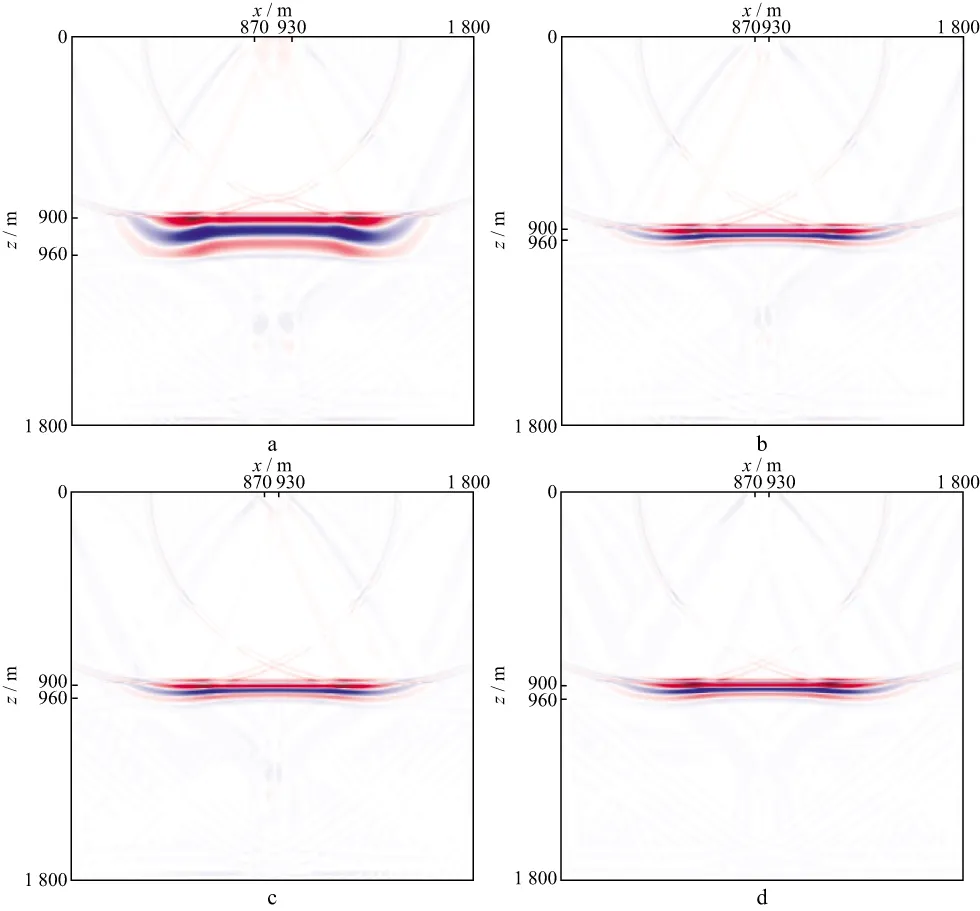
图7 可变网格与传统网格逆时偏移剖面a 可变网格逆时偏移; b 校正后可变网格逆时偏移; c 传统粗网格逆时偏移; d 传统细网格逆时偏移

图8 含孔洞介质模型
2.3复杂介质模型
为了分析可变网格逆时偏移算法对复杂介质的适用性,选用Marmousi模型(图10)对可变网格逆时偏移算法进行了测试。模型总大小为9200m×3000m,可变网格逆时偏移在矩形虚线区域网格大小为4m×4m,其它区域(除过渡带外)网格大小为12m×12m,时间采样步长为0.25ms;传统粗网格逆时偏移网格大小为12m×12m,时间采样步长为1ms。震源起始位置(12m,12m),炮间距48m,总炮数为191炮;检波器位于地表,道间距为12m。采用检波器固定、炮点向右移动的方式进行数值模拟,接收时间长度为3.0s,震源为主频35Hz的Ricker子波。

图9 可变网格与传统常规网格逆时偏移剖面a 传统粗网格逆时偏移; b 传统细网格逆时偏移; c 可变网格逆时偏移

网格类型网格大小计算时间/h相对传统粗网格的计算时间倍数传统粗网格6m×6m8.41.00可变网格粗网格6m×6m,细网格2m×2m26.03.09传统细网格2m×2m148.517.67

图10 Marmousi模型
图11为滤波前和滤波后可变网格逆时偏移剖面,滤波后偏移剖面彻底消除了逆时偏移互相关成像低频噪声的影响,中浅部断裂及深部不整合接触关系均得到了较好成像。从偏移成像效果分析,采用本文算法并没有在大/小尺度网格边界产生人为的异常反射,进一步显示了本文算法对于复杂介质的有效性。图12为常规粗网格与可变网格逆时偏移局部剖面对比,常规粗网格逆时偏移由于大尺度网格步长导致单个波长内采样不足产生了明显的数值频散,而可变网格逆时偏移不仅使成像精度得到了提高,偏移效率也得到了提高。

图11 滤波前(a)、后(b)可变网格逆时偏移剖面对比

图12 常规粗网格与可变网格逆时偏移局部剖面对比a 粗网格逆时偏移; b 可变网格逆时偏移
3 结束语
本文采用多尺度可变网格有限差分算法求解一阶应力-速度声波方程,对传统常规逆时偏移算法进行了改进,通过理论推导和模型试验,验证了可变网格高阶有限差分法逆时偏移能在保证地下地质体成像精度的同时大幅度提高计算效率,特别是小尺度构造的成像尤为明显。
但是,由于时间步长未采用可变算法,在数值模拟试验中还存在不稳定现象,建议将变空间步长与变时间步长相结合,进一步提高可变网格逆时偏移算法的稳定性。
[1]WHITMORE N D.Iterative depth migration by backward time propagation[J].Expanded Abstracts of 53rdAnnual Internat SEG Mtg,1983:382-385
[2]KARAZINCIR M H,GERRARD C M.An efficient 3D reverse time pre-stack depth migration[J].Expanded Abstracts of 68thEAGE Conference & Exhibiton,2006:261-262
[3]ETGEN J,O’BRIEN M.Computational methods for large-scale 3D acoustic finite-difference modeling:a tutorial[J].Geophysics,2006,71(5):223-230
[4]SYMES W W.Reverse time migration with optimal checkpointing[J].Geophysics,2007,72(5):SM213-SM221
[5]CLAPP R G.Reverse time migration with random boundaries[J].Expanded Abstracts of 79thAnnual Internat SEG Mtg,2009:2809-2813
[6]BAYSAL E,KOSLOFF D D,SHERWOOD J W C.Reverse time migration[J].Geophysics,1983,48(11):1514-1524
[7]LIU F Q,ZHANG G Q,MORTON S A.An effective imaging condition for reverse-time migration using wavefield decomposition[J].Geophysics,2011,76(1):S29-S39
[8]YOON K,MARFURT K J.Reverse-time migration using the Poynting vector[J].Exploration Geophysics,2006,37(1):102-107
[9]唐祥功,匡斌,杜继修,等.多GPU协同三维叠前逆时偏移方法研究与应用[J].石油地球物理勘探,2013,48(6):910-914
TANG X G,KUANG B,DU J X,et al.3D prestack reverse time migration based on multiple-GPU collaboration[J].Oil Geophysical Prospecting,2013,48(6):910-914
[10]董良国,马在田,曹景忠.一阶弹性波方程交错网格高阶差分解法稳定性研究[J].地球物理学报,2000,43(6):856-863
DONG L G,MA Z T,CAO J Z.A study on stability of the staggered-grid high-order difference method of first-order elastic wave equation[J].Chinese Journal Geophysics,2000,43(6):856-863
[11]MOCZO P.Finite-difference technique for SH waves in 2D media,using irregular grids:application to the seismic response problem[J].Geophysical Journal International,1989,99(2):321-329
[12]JASTRAM C,BEHLE A.Acoustic modeling on a grid of vertically varying spacing[J].Geophysical Prospecting,1992,40(2):157-169
[13]WANG Y,XU J,SCHUSTER G T.Viscoelastic wave simulation in basins by a variable-grid finite-difference method[J].Bulletin of the Seismological Society of America,2001,91(6):1741-1749
[14]李振春,张慧,张华.一阶弹性波方程的变网格高阶有限差分数值模拟[J].石油地球物理勘探,2008,43(6):711-716
LI Z C,ZHANG H,ZHANG H.Variable-grid high-order finite-difference numeric simulation of first-order elastic wave equation[J].Oil Geophysical Prospecting,2008,43(6):711-716
[15]孙成禹,李胜军,倪长宽,等.波动方程变网格步长有限差分数值模拟[J].石油物探,2008,47(2):123-128
SUN C Y,LI S J,NI C K,et al.Wave equation numerical modeling on a mesh of varying spacing[J].Geophysical Prospecting for Petroleum,2008,47(2):123-128
[16]黄超,董良国.可变网格与局部时间步长的高阶差分地震波数值模拟[J].地球物理学报,2009,52(1):176-186
HUANG C,DONG L G.High-order finite-difference method in seismic wave simulation with variable grids and local time-steps[J].Chinese Journal Geophysics,2009,52(1):176-186
[17]何兵寿,张会星,魏修成,等.双程声波方程叠前逆时深度偏移的成像条件[J].石油地球物理勘探,2010,45(2):237-243
HE B S,ZHANG H X,WEI X C,et al.Imaging conditions for two-way acoustic wave equation pre-stack revers-time depth migration[J].Oil Geophysical Prospecting,2010,45(2):237-243
[18]陈康,吴国忱.逆时偏移拉普拉斯算子滤波改进算法[J].石油地球物理勘探,2012,47(2):249-255
CHEN K,WU G C.An improved filter algorithm based on Laplace operator in reverse-time migration[J].Oil Geophysical Prospecting,2012,47(2):249-255
[19]郭鹏,何兵寿,郭敏.基于坡印亭矢量的声波方程叠前逆时偏移成像条件[J].煤炭学报,2011,36(8):1290-1295
GUO P,HE B S,GUO M.Acoustic equation pre-stack reverse-time migration imaging condition based on Poynting vector[J].Journal of China Coal Society,2011,36(8):1290-1295
[20]CHEN T,HE B S.A normalized wavefield separation cross-correlation imaging condition for reverse time migration based on Poynting vector[J].Applied Geophysics,2014,11(2):158-166
[21]孙成禹,宫同举,张玉亮,等.波动方程有限差分法中的频散与假频分析[J].石油地球物理勘探,2009,44(1):43-48
SUN C Y,GONG T J,ZHANG Y L,et al.Analysis on dispersion and alias in finite-difference solution of wave equation[J].Oil Geophysical Prospecting,2009,44(1):43-48
(编辑:戴春秋)
Acoustic pre-stack reverse time migration using variable grid finite-difference method
MA Guangke,LI Yangsen,SUN Wanyuan,LIU Feng,LIAO Xianfeng
(ZhanjiangBranchCompany,ChinaNationalOffshoreOilCorporation,Zhanjiang524000,China)
During reverse time migration imaging (RTM) using the high-order finite-difference method,imaging accuracy and computational efficiency is a pair of contradiction,especially for the fine migration of small-scale geological structure.In order to fine characterize the structure of local geological structure while ensuring the RTM computational efficiency,a multi-scale variable grid finite-difference method is used to solve the first-order stress-velocity acoustic wave equation.The variable grid finite-difference algorithm is introduced to RTM to improve the traditional RTM algorithm.The variation range of the variable grid step is extended to any odd times.Furthermore,the numerical dispersion is analyzed in the process of variable grid finite-difference algorithm.The variable grid RTM test results for different models show that the variable grid RTM algorithm can improve the imaging accuracy of subsurface geological structure and improve the migration efficiency,which is beneficial for the fine description of the local structural features.
reverse time migration (RTM),variable grid,staggered grid,depth migration
2015-10-22;改回日期:2016-02-16。
马光克(1975—),男,硕士,高级工程师,主要从事油气田开发地震研究工作。
中海石油(中国)有限公司湛江分公司综合科研项目“东方气田群高温高压天然气藏开发关键技术研究”(YXKY-2016-ZHJ-02)资助。
P631
A
1000-1441(2016)05-0728-09
10.3969/j.issn.1000-1441.2016.05.012
This research is financially supported by the Comprehensive Scientific Research Project of Zhanjiang Branch Company of China National Offshore Oil Corporation (Grant No.YXKY-2016-ZHJ-02).

