基于Shearlet变换稀疏约束地震数据重建
冯 飞,王 征,刘成明,王德利
(1.中海油田服务股份有限公司,天津300451;2.吉林大学地球探测科学与技术学院,吉林长春130026)
基于Shearlet变换稀疏约束地震数据重建
冯飞1,王征1,刘成明2,王德利2
(1.中海油田服务股份有限公司,天津300451;2.吉林大学地球探测科学与技术学院,吉林长春130026)
地震数据重建是地震数据处理流程中关键步骤之一,重建效果的好坏直接影响到后续的多次波消除以及偏移成像效果。为了获得更好的重建效果,提出了以压缩感知为理论基础,采用jitter欠采样的Shearlet变换稀疏约束地震数据重建方法。将Shearlet变换与凸集投影(POCS)算法结合起来在动校正预处理后对地震数据进行重建,增强了地震数据在Shearlet域的稀疏性。理论分析和实际地震数据验证结果表明,该方法可以在部分地震数据缺失的情况下取得很好的重建效果,有效地解决了假频问题。
Shearlet变换;数据重建;稀疏变换;压缩感知;jitter欠采样
地震数据采集过程中,受野外采集地质环境、仪器故障、人为干扰、噪声以及经济条件等因素的影响,采集系统很难记录完整的地震波场信息,采集到的数据往往会出现缺失道和野值道。这些不规则的或者稀疏的地震数据不仅会产生假频,也为偏移成像和多次波衰减带来了影响,从而不能提供精确、规则的地震信号,给数据的处理与解释工作造成了一定的困扰。因此,地震数据重建成为地震数据处理中的关键步骤之一。
在实际地震勘探中,很多数据重建方法已经取得了良好的效果,大致可以将其分为3类:①基于信号处理的方法[1],将地震数据从时间域转换到变换域,根据变换域内信号的特征进行重建,如:傅里叶域、小波域、Curvelet域等,这类方法的处理效果在很大程度上依赖于数学变换的好坏;②基于波动方程的方法[2],根据地震波场在地下介质中传播的物理特征完成重建,这类方法需要地下的速度信息,并且计算量很大,因此并没有广泛应用;③基于预测滤波的数据重建方法,这类方法主要利用分频预测的思想,用低频信息预测高频信息,主要有f-x域预测滤波[3]、f-k域预测滤波[4]以及t-x域预测滤波。
基于信号处理的方法常见的是傅里叶变换和小波变换,这两种方法对于线性同相轴能取得很好的重建效果,但对于弯曲同相轴的效果很难令人满意。近年来发展起来的Shearlet变换与小波变换不同,Shearlet变换有各向异性基,近似满足抛物线比例,且在频率域严格局部化,因而Shearlet变换能够更好地表示地震波场特征。与Curvelet变换类似,Shearlet变换是一种多尺度稀疏变换,并且具有更好的方向性、稀疏性以及更加简单的数学结构。目前,Shearlet变换已经在图像处理领域得到广泛应用,但尚未广泛应用到地震数据处理领域。在地震数据处理领域中,Curvelet变换在地震数据去噪[5-6]与稀疏重建中得到了广泛的应用。
地震数据重建问题可以转化为一个稀疏优化问题,压缩感知理论[7-8]的提出,使得在大量数据缺失的情况下仍然可以很好恢复出地震数据(即使在低于香农采样定理的情况下)。其重构的关键在于数据的稀疏性,但是地震信号往往并不是稀疏的,如果将这些信号转换到某些变换域,使得信号在这些变换域内的大多数系数为零或者很小,并且绝大多数重要的信号在变换域内的系数较大,较大的系数保留了信号绝大部分信息,使得信号在变换域是稀疏的。因此,稀疏变换成为压缩感知理论应用的关键,通过某些稀疏优化解法可以对缺失数据进行重构。HERRMANN等[9]利用Curvelet变换通过L1范数最优化解法对地震数据进行重建,相对常规重建方法效果有很大的提升。Curvelet变换成为压缩感知关键的组成部分,之后这种稀疏变换迅速发展。周亚同等[10]采用离散余弦变换(DCT)与曲波字典组合进行稀疏重建。路交通等[11]在Curvelet变换的基础上进行了改进,取得了较好的效果。
本文对地震数据重建问题的求解过程可以理解为压缩感知理论范畴,压缩感知的3个组成部分分别是稀疏变换、采样方式以及求解方法。首先,采用Shearlet变换作为数据重建的稀疏变换代替了Curvelet变换,Shearlet变换比Curvelet变换有更好的稀疏性,同时对地震数据采取jitter欠采样方式(jitter欠采样方式很大程度上模拟了野外地震数据采集中遇到的实际问题,避免采用随机采样引起间隔过大,同时又保证一定的随机性,规则采样的假频在一定程度上比jitter采样更加严重,对地震数据的重构影响更大),与常规的规则采样和随机采样方法相比,有效地提高了重构精度;其次,将地震数据重建描述为图像修复的过程,通过Shearlet变换的L1范数最优化求解,采用凸集投影算法(POCS)对地震数据进行重建,有效地提高了重建效率;最后,对地震数据进行动校正预处理后进行重建,动校正预处理的Shearlet变换的重建效果较好,与传统的小波重建和Curvelet变换重建相比具有明显的优势。
1 Shearlet变换
2005年以来,许多学者[12-17]将复合小波理论和几何多尺度分析联系到一起,通过特殊形式的具有合成膨胀的仿射系统构造了一种接近最优的多维函数稀疏表示方法——Shearlet变换,有着比曲波和轮廓波更敏感的方向性和更好的稀疏表示性质。
在二维情况下合成仿射系统的形式为:
φAS(ψ)={ψa,s,t(x)=|detA|a/2·
ψ[AaSs(x-t)]:a,s∈Z,t∈Z2}
(1)
式中:A和S为2×2可逆矩阵,|detS|=1。那么剪切波系统的基本单元复合小波为φAS(ψ),由复合小波构成了如下Parseval框架(紧框架条件):
(2)
式中:f∈L2(R2)。在上述Shearlet系统中,各向异性对角矩阵Aa为Shearlet尺度矩阵,Ss为Shearlet剪切矩阵,其中,a,s分别为尺度参数和剪切参数,对∀a>0,s∈R,有:
(3)
在上述系统下,令ψ∈L2(R2)满足:
(4)
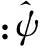
在上述仿射系统下,由Shearlet母函数ψ,各向异性膨胀矩阵Aa和剪切矩阵Ss构建了剪切波系统:
(5)
a∈R+s∈Rt∈R2
基于数学变换的信号处理,其结果好坏主要取决于数学变换对有效信号的逼近程度和信号在变换域的稀疏性。
首先,图1a,图1b和图1c分别展示了Meyer小波、Curvelet变换以及Shearlet变换的频率域剖分[18]:Meyer小波基——正则化的小波基可以很好地表示各向同性数据;Curvelet基——具有方向性的紧支撑框架,精细尺度可以很好地表示各向异性数据;Shearlet基——具有方向性的紧支撑框架,精细尺度可以很好地表示各向异性数据;且在连续系统和离散系统之间的转变也更加灵活自然,是目前多尺度领域唯一可以将连续系统和数字系统统一处理的变换方法。
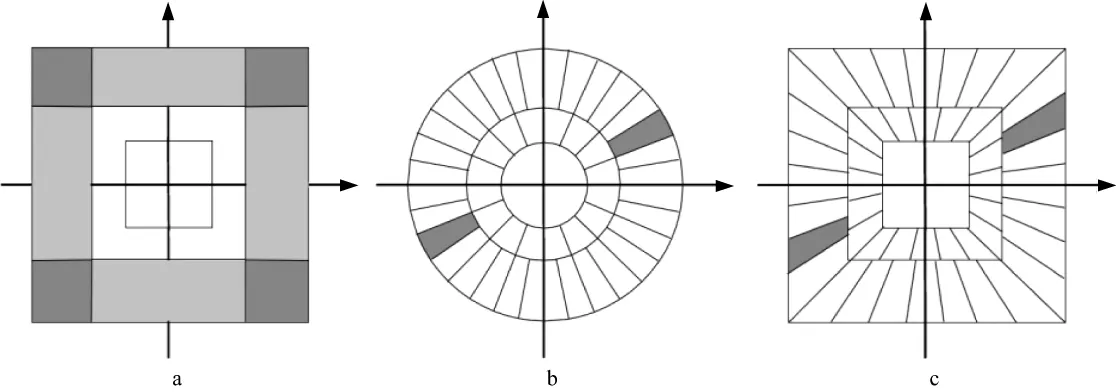
图1 多尺度变换频率域剖分a Meyer小波; b Curvelet变换; c Shearlet变换
其次,相对于傅里叶变换、小波变换、Curvelet变换在它们各自的域中得到的稀疏系数,Shearlet变换系数具有更加稀疏的特性[19],但在地震数据处理领域还没有得到广泛的应用。
2 稀疏变换域L1范数约束的缺失道地震数据重建
2.1结合Shearlet变换的POCS地震数据重建
假设完整的地震数据为A,y为缺失的地震数据,M为地震数据的一个缺失算子,与数据缺失位置对应的元素为0,其它元素为1。那么地震数据重建的问题可以归结为L1范数最优化问题,即:
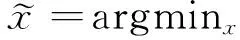
(6)
式中:A=S-1x,其中,S-1为Shearlet逆变换,x为一组Shearlet系数。即将问题转换到Shearlet域重构出地震数据A,反演出一组L1范数最小的Shearlet系数x,可以利用如下约束最优化问题来表示稀疏约束情况下重建问题:
(7)
为了解决上述约束最优化问题,GERSZTENKORN等[20]提出迭代重加权最小平方法(IRLS),BERG等[21]提出SPGL1算法以及各种阈值迭代方法求解。但是上述求解方法过于繁琐,计算量很大,利用凸集投影理论(POCS)[22-23]求解此类问题使求解过程变得简单。结合POCS算法的Shearlet域稀疏约束地震数据重建基本步骤如下。
1) 初始化。
设置误差参数ε,迭代次数N以及阈值参数δ;
初始化Xm=XM,Xi=0(X为完整地震数据,Xm为缺失数据);
令λ=1,δ为Shearlet系数的最大归一化系数。
2) 阈值迭代。
计算缺失数据R=M(Xm-Xi);
进行Shearlet变换x=S(R+Xi);
作阈值,Shearlet逆变换求重建后地震数据Xi=ST[T(x)]。
3) 更新阈值迭代。
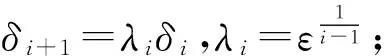
(8)
为了加快收敛速度,本文选用指数衰减的阈值代替线性阈值,其中λi=ε1/(i-1)。求解上述优化问题就是反演一组Shearlet系数x,且该组数据满足经缺失算子作用后与原始数据在二范数约束下最接近。因此,最终的输出就是这组Shearlet系数逆变换的结果,代表了重建后的数据。
2.2观测系统的采样方式
采样方式是压缩感知的重要组成部分,直接影响到数据的稀疏性。地震勘探通常在地面观测,采样方式有限,常见的有规则采样和随机采样。由于地质条件等因素的限制,往往不允许采取规则采样,且规则采样产生的假频信息很多,不利于后续的数据处理工作;而随机采样能减少假频,但是很难保证采样间隔,容易出现采样点过于聚集或者过于分散的状况。当数据不存在随机性或者缺失过大时,Shearlet稀疏重建效果与Curvelet稀疏重建效果类似,数据重构结果都不够理想。对于规则采样和随机采样数据重建,很多学者进行了研究[24],这里不再赘述。HENNENFENT等[25]引进了一种jitter采样方式,这种方法兼具了规则采样方式和随机采样方式的优势,既能控制采样间隔又能保持采样点的随机性。首先将目标区域等间隔采样,然后以这些采样点为中心随机扰动,为了说明jitter采样方式,假设采样因子γ为奇数(γ=1,3,5,…),总采样点是γ的倍数,采样的样点数为n=N/γ取整数,这里,可以给出的jitter采样点为:
(9)
离散随机变量εi是独立的整数,且在采样间隔[-(ξ-1)/2,(ξ-1)/2]内均匀分布,jitter参数ξ(0≤ξ≤γ)表示粗糙网格下的jitter大小,当ξ=γ时为最优jitter采样[26]。
2.3动校正预处理下的地震数据重建
野外采集地震数据时,当地面水平、反射界面为平面且界面内介质均匀时,反射时距曲线为一条双曲线,不能直接反映地下界面的起伏情况,只有在激发点处接收的t0时间,才能直接反应界面的真深度。因此,我们可以对其进行动校正,即把炮检距不同的道上来自同一界面、同一点的反射波到达时间,校正为共中心点处的回声时间,从而实现同相叠加。
由于Shearlet变换是一种多尺度变换,它的结构元素除了包括尺度参数和平移参数,还包括剪切参数,所以Shearlet函数具有很好的方向选择性和各向异性,可以很好地表示各向异性地震波场。基于Shearlet变换稀疏约束重建的关键在于地震数据在Shearlet域的稀疏性,稀疏性越好意味着我们可以利用越少的系数对地震数据达到精确重建。因此,为了使地震数据在Shearlet域更加稀疏,利用Shearlet变换重建的地震数据做动校正预处理,动校正之后的数据同相轴更加平缓,在一定程度上降低了假频影响,更重要的是,相比于曲率过大的同相轴,在Shearlet域中可以用更少的系数表示地震同相轴信息,其稀疏性将会更好,相应地,Shearlet域中的重构误差将会减小,重建之后再反动校正回来,从而达到更好的重建效果。WANG等[27]将这种预动校正处理的方法与Curvelet变换结合对地震数据进行重建,也取得了较好的效果。
3 模型及实际数据测试
3.1模型数据测试
为了验证Sheratlet变换在地震数据重建中的效果,先对一个合成地震数据采用jitter欠采样后进行重建。该地震记录共361道,道间距25m,采样间隔4ms。首先分别利用Curvelet变换迭代法、Shearlet变换迭代法对缺失地震数据重建,其次对缺失的地震数据进行动校正预处理,然后再利用Curvelet变换迭代法和Shearlet变换迭代对缺失的地震数据进行重建。
图2显示了原始地震数据以及缺失比为50%,75%的地震数据(设定最大连续缺失道为5道)。
图3显示了采用不同方法对缺失比为50%的地震数据(jitter欠采样)进行重建的结果。下面比较不同方法的重建效果,并分析产生的假频以及重建后对假频的压制效果。图3a和图3b是缺失比为50%地震数据(图2b)经过Curvelet重建后的地震记录及差剖面,可见,重建取得了一定的效果,但是同相轴连续性不好,差剖面中同相轴剩余能量很强。图3c和图3d分别为经动校正预处理过后再经Curvelet变换重建后的地震记录及差剖面,可以明显看出,相比未经动校正处理的地震数据重建后同相轴变得光滑连续,并且差剖面残余能量更少。图3e和图3f分别为经Shearlet变换重建后地震记录及差剖面,相对于图3a和图3b,同相轴几乎完美重构,差剖面也少见残余能量,而经动校正预处理(图3g,图3h)后,重建效果仍然好于未经动校正预处理过的重建效果。
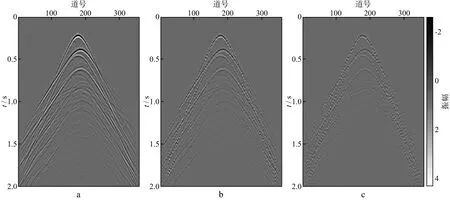
图2 模拟地震数据及jitter欠采样地震数据a 原始地震数据; b 缺失比为50%的地震数据; c 缺失比为75%的地震数据

图3 缺失比为50%的地震数据重建结果a,b 分别为Curvelet重建后的地震记录及差剖面; c,d 分别为预动校正处理后再经Curvelet重建的地震记录及差剖面; e,f 分别为Shearlet重建后的地震记录及差剖面; g,h 分别为预动校正处理后再经Shearlet重建的地震记录及差剖面
为了进一步验证基于Shearlet变换对大量数据缺失情况下重建的效果,对缺失比为75%的地震数据做同样的处理,得到的结果如图4所示。
从图4可以很明显看出,基于Shearlet变换的地震数据重建效果要好于Curvelet变换的重建效果,并且经动校正预处理后的重建效果更好,尤其在同相轴曲率大的部分。这是由于稀疏变换时利用各向异性小波对同相轴逼近,对同一数据而言,Shearlet的基函数可以取得比Curvelet的基函数更好的逼近效果,而当同相轴曲率很大时,逼近效果都有所欠缺,经动校正预处理后的地震记录同相轴相对较为平滑,能取得较好的逼近效果。
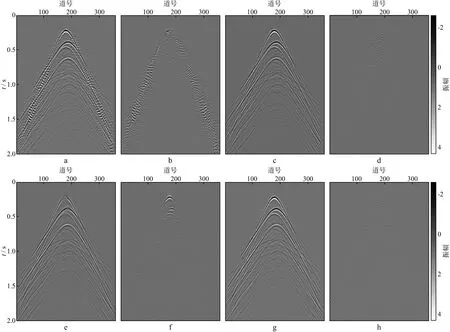
图4 缺失75%地震数据重建结果a,b 分别为Curvelet重建后的地震记录及差剖面; c,d 分别为预动校正处理后再经Curvelet重建的地震记录及差剖面; e,f 分别为Shearlet重建后的地震记录及差剖面; g,h 分别为预动校正处理后再经Shearlet重建的地震记录及差剖面
为了展示Shearlet变换重建对假频信息的压制效果,选取了缺失比为50%的地震数据,并对重建后的地震数据作f-k谱分析。图5a,图5b分别是原始地震数据和缺失比为50%的地震数据的f-k谱,可见,缺失地震数据的f-k谱出现了严重的假频。采用不同方法对缺失比为50%的地震数据进行重建,结果如图6所示。从图6可以看出,经过Curvelet方法重建后,假频信息得到了较好的压制,但是部分频率的信息有所缺失;而Shearlet变换重建对假频的压制效果明显更好;经过动校正预处理的重建效果好于未经动校正处理的重建效果。
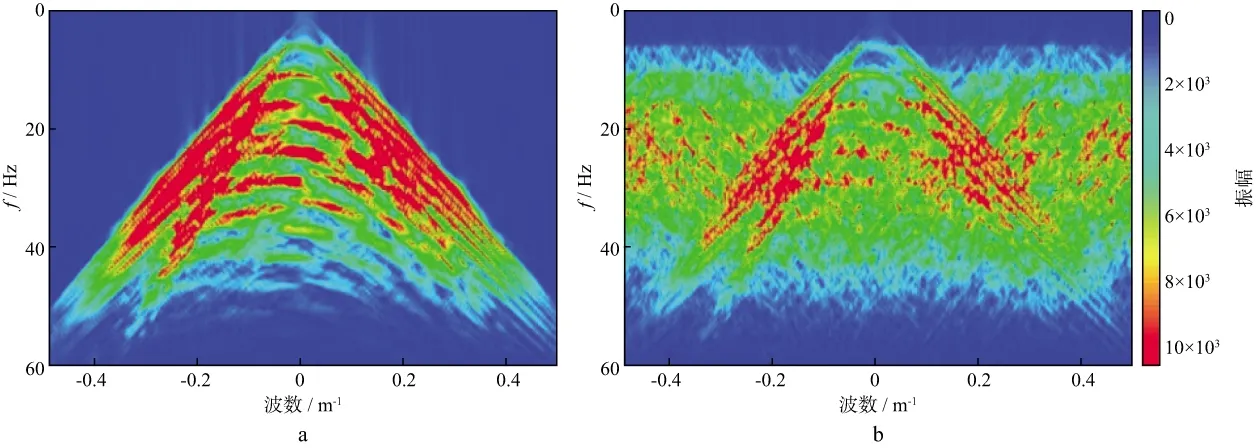
图5 原始地震数据(a)和缺失比为50%的缺道地震数据(b)的f-k谱
3.2实际数据测试
为了进一步验证Shearlet变换稀疏约束地震数据重建在实际地震数据处理中的效果,选取某实际地震记录(图7a)进行重建,缺失的地震数据(图7b)缺失比为50%,重建效果如图8至图11所示。
图8与图9分别展示了Curvelet变换与Shearlet变换重构数据的结果与图7a的差剖面,可见,Shearlet变换重构效果要好于Curvelet变换重构效果。图10与图11分别展示了经过动校正预处理的Curvelet变换与Shearlet变换的重建效果以及与图7a差剖面,同样可以看出,Shearlet变换重建数据与实际数据差值最小。

图7 实际数据(a)和缺失比为50%的地震数据(b)
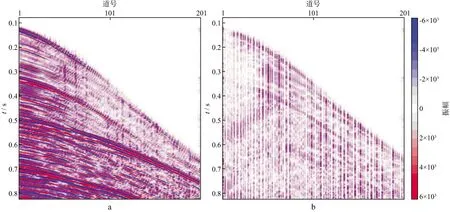
图8 Curvelet重建结果(a)及与实际数据的差剖面(b)

图9 Shearlet重建结果(a)及与实际数据的差剖面(b)
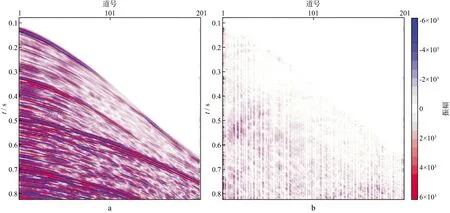
图10 动校正后Curvelet重建结果(a)及与实际数据的差剖面(b)
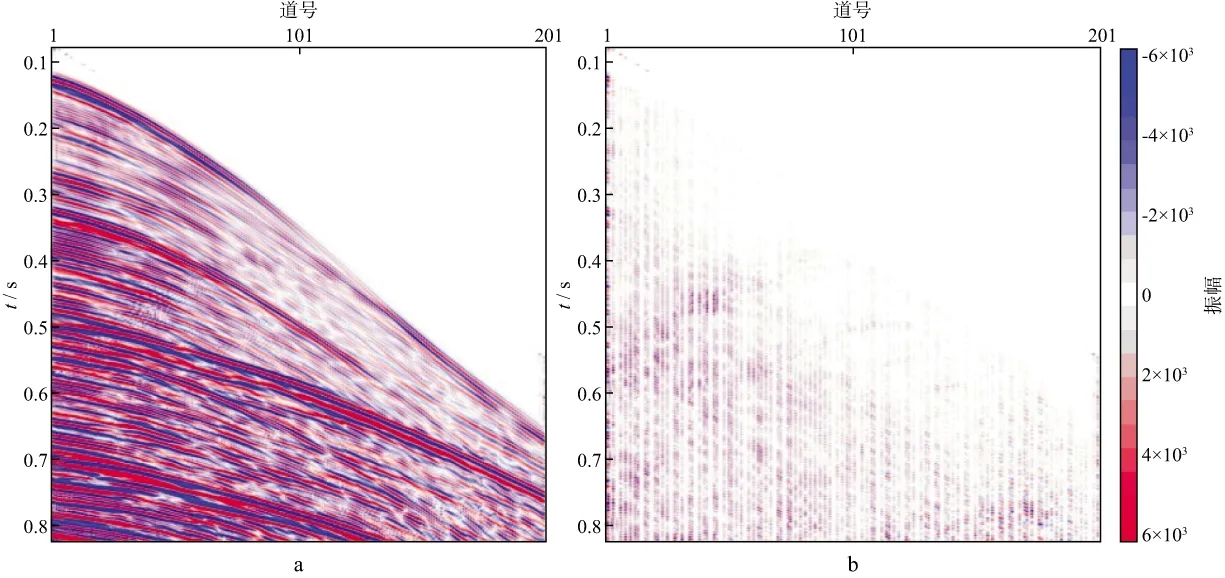
图11 动校正后Shearlet重建结果(a)及与实际数据的差剖面(b)
4 结束语
1) 本文采用POCS算法将Shearlet变换算子引进到地震数据重建中,验证了Shearlet变换能够在jitter欠采样中地震数据缺失的情况下,比Curvelet变换更能有效重构出地震数据;从理论数据与实际数据的f-k谱中能够看出有效压制了由缺失道引起的假频,经过动校正预处理的重构效果更佳,为地震数据波场重构提供了新的技术思路。
2) Shearlet变换较Curvelet变换的数学表达更加简洁,因此运算时间比Curvelet变换减少一半,但要大规模应用到野外海量地震数据处理,还需要进一步提高运算效率。
3) 目前野外地震数据大规模采用了三维采集,将三维Shearlet变换应用于三维地震数据重建将是未来该方法研究的方向之一。
[1]刘国昌,陈小宏,郭志峰,等.基于Curvelet变换的缺失地震数据重建方法[J].石油地球物理勘探,2011,46(2):237-246
LIU G C,CHEN X H,GUO Z F,et al.Missing seismic data rebuilding by interpolation based on curvelet transform[J].Oil Geophysical Prospecting,2011,46(2):237-246
[2]RONEN J.Wave-equation trace interpolation[J].Geophysics,1987,52(7):973-984
[3]SPITZ S.Seismic trace interpolation in theF-Xdomain[J].Geophysics,1991,56(6):785-794
[4]GULUNAY N,CHAMBERS R E.Unaliasedf-kdomain trace interpolation[J].Expanded Abstracts of 66thAnnual Internat SEG Mtg,1996:1685-1688
[5]张之涵,孙成禹,姚永强,等.三维曲波变换在地震资料去噪处理中的应用研究[J].石油物探,2014,53(4):421-430
ZHANG Z H,SUN C Y,YAO Y Q,et al.Research on the application of 3D curvelet transform to seismic data denoising[J].Geophysical Prospecting for Petroleum,2014,53(4):421-430
[6]孟阁阁,王德利,陈鑫.基于三维曲波变换的地震数据去噪方法研究[J].石油物探,2014,53(3):313-323
MENG G G,WANG D L,CHEN X.Study on seismic data denoising method based on 3D Curvelet transform[J].Geophysical Prospecting for Petroleum,2014,53(3):313-323
[7]DONOHO D L.Compressed sensing[J].IEEE Transactions on Information Theory,2006,52(4):1289-1306
[9]HERRMANN F J,HENNENFENT G.Non-parametric seismic data recovery with Curvelet frames[J].Geophysical Journal International,2008,173(1):233-248
[10]周亚同,刘志峰,张志伟.形态分量分析框架下基于DCT与曲波字典组合的地震信号重建[J].石油物探,2015,54(5):560-568
ZHOU Y T,LIU Z F,ZHANG Z W.Seismic signal reconstruction under the morphological component analysis framework combined with discrete cosine transform (DCT) and curvelet dictionary[J].Geophysical Prospecting for Petroleum,2015,54(5):560-568
[11]路交通,曹思远,董建华.基于稀疏变换的地震数据重构方法[J].物探与化探,2013,37(1):175-179
LU J T,CAO S Y,DONG J H.A study of seismic data recovery based on sparse transform[J].Geophysical&Geochemical Exploration,2013,37(1):175-179
[12]GUO K,KUTYNIOK G,LABATE D.Sparse multid,imensional representations using anisotropic dilation and shear operators[J].International Conference on the Interaction Between Wavelets & Splines,2005:189-201
[13]LABATE D,LIM W Q,KUTYNIOK G,et al.Sparse multidimensional representation using Shearlets[J].Proceedings of SPIE,2005,5914(1):254-262
[14]KUTYNIOK G,SHAHRAM M,ZHUANG X.Shearlab:a rational design of a digital parabolic scaling algorithm[J].Siam Journal on Imaging Sciences,2012,5(4):1291-1332
[15]GUO K,LABATE D.The construction of smooth parseval frames of Shearlets[J].Mathematical Modelling of Natural Phenomena,2013,8(1):82-105
[16]KITTIPOOM P,KUTYNIOK G,LIM W Q.Construction of compactly supported Shearlet frames[J].Constructive Approximation,2012,35(1):21-72
[17]GUO K,LABATE D.Optimally sparse multidimensional representation using Shearlets[J].SIAM Journal on Mathematical Analysis,2007,39(1):298-318
[18]DONOHO D L,KUTYNIOK G.Geometric separation using a wavelet-Shearlet dictionary[J].SAMPTA2009:International Conference on Sampling Theory and Applications,2009:223-238
[19]刘成明,王德利,王通,等.基于Shearlet变换的地震随机噪声压制[J].石油学报,2014,35(4):692-699
LIU C M,WANG D L,WANG T,et al.Random
seismic noise attenuation based on the Shearlet transform[J].Acta Petrolei Sinica,2014,35(4):692-699
[20]GERSZTENKORN A,BEDNAR J B,LINES L R.Robust iterative inversion for the one-dimensional acoustic wave equation[J].Geophysics,1986,51(2):357-368
[21]VAN DEN BERG E,FRIEDLANDER M P.Probing the Pareto frontier for basis pursuit solutions[J].SIAM Journal on Scientific Computing,2008,31(2):890-912
[22]BREGMAN L M.The method of successive projection for finding a common point of convex sets[J].Soviet Mathematics Doklady,1965,6(3):688-692
[23]ABMA R,KABIR N.3D interpolation of irregular data with a POCS algorithm[J].Geophysics,2006,71(6):E91-E97
[24]张华,陈小宏.基于jitter采样和曲波变换的三维地震数据重建[J].地球物理学报,2013,56(5):1637-1649
ZHANG H,CHEN X H.Seismic data reconstruction based on jittered sampling and curvelet transform[J].Chinese Journal of Geophysics,2013,56(5):1637-1649
[25]HENNENFENT G,HERRMANN F J.Simply denoise:wavefield reconstruction via jittered undersampling[J].Geophysics,2008,73(3):V19-V28
[26]LENEMAN O.Random sampling of random processes:impluse response[J].Information and Control,1966,9(2):2181-2188
[27]WANG D L,BAO W Q,XU S B,et al.Seismic data interpolation with Curvelet domain sparse constrained inversion[J].Journal of Seismic Exploration,2014,23(1):492-499
(编辑:顾石庆)
Seismic data reconstruction based on sparse constraint in the Shearlet domain
FENG Fei1,WANG Zheng1,LIU Chengming2,WANG Deli2
(1.ChinaOilfieldServicesLimited,Tianjin300451,China;2.CollegeofGeo-ExplorationScienceandTechnology,JilinUniversity,Changchun130026,China)
Seismic data reconstruction is a key step in seismic data processing.Reconstruction result will directly affect the multiple elimination and subsequent migration imaging.To get better reconstruction result,on the basis of the theory of compressed sensing,a new seismic data reconstruction method based on the Shearlet transform sparse constraint using jittered undersampling is proposed.Shearlet transform is a kind of multi-scale transform to express multi-dimensional data well,which has the optimal sparseness,orientation and the characteristics of localization.We combine the Shearlet transform with the projection onto convex sets (POCS) algorithm for seismic data reconstruction.Then we conduct normal moveout correction (NMO) prior to reconstruction to streng then the sparseness of the seismic data in the Shearlet domain.The experiments on synthetic data as well as actual data show that even though some seismic data are missing,the reconstruction method based on the Shearlet transform performs excellent and effectively solves the aliasing problem.
Shearlet transform,data reconstruction,sparse transform,compressed sensing,jittered undersampling
2015-09-22;改回日期:2016-02-27。
冯飞(1986—),男,博士,现主要从事高精度地震数据处理方法研究。
国家科技重大专项(2011ZX05023-005-008)和国家自然科学基金(41374108)共同资助。
P631
A
1000-1441(2016)05-0682-10
10.3969/j.issn.1000-1441.2016.05.007
This research is financially supported by the National Science and Technology Major Project of China (Grant No.2011ZX05023-005-008) and the National Science Foundation of China (Grant No.41374108 ).
——工程地质勘察中,一种做交叉剖面的新方法

