BGN-型类同态IBE方案的构造与分析

戴晓明　张　薇　郑志恒

(武警工程大学信息安全保密重点实验室　陕西 西安 710086)



BGN-型类同态IBE方案的构造与分析

戴晓明张薇郑志恒

(武警工程大学信息安全保密重点实验室陕西 西安 710086)

基于身份的公钥密码体制(IBE)与传统的公钥密码体制不同，在IBE中用户公钥是与用户身份相关的可识别的一串字符，这就为加密后的数据提供了更灵活的访问控制。BGN是2005年提出的一种类同态加密方案，该方案能对密文进行任意次加法和一次乘法运算，但是并不是一种IBE方案。为得到类同态的IBE方案，以满足网络中对身份类加密体制的需求，在BGN方案的基础上，基于二次剩余假设和子群判定问题构造了一种新的具有类同态性质的IBSHE加密方案，在随机预言机模型下证明了该方案的CPA安全性。

同态加密基于身份的加密双线性映射二次剩余问题子群判定问题

0　引　言

加密体制的同态性已成为新型密码体制的一个重要设计目标。具有同态性质的加密方案允许在服务器端直接对密文进行运算，用户只需对返回的密文结果解密即可，所以同态密码在保证数据安全性的同时，能显著降低数据服务的通信量及运算量。因而将同态加密与具体应用相结合，借鉴成熟的数学工具，构造满足实际应用需要的高效的新型同态加密方案，深入研究同态加密体制在具体场合的应用，并构造相关的应用协议，具有十分重要的理论和实践意义。

1995年，Benaloh[1]提出了一种支持有限次加法操作的密码体制，这是第一个以同态性为设计目标的公钥密码，随后产生的各种同态加密方案都只支持加法操作。直到2005年，Boneh等[2]提出了BGN方案，该方案可对密文做一次乘法和任意多次加法运算，是自同态加密被提出以来的首个类同态加密方案，方案被证明在密文不可区分的选择明文攻击下(Ciphertext indistinguishability under chosen plaintext attacks:IND-CPA)安全。2010年，Gentry等在格上实现了BGN方案[3]。2009年，Gentry[4]开创性地利用自举和压缩的构造方法，提出了一个基于理想格的全同态加密方案。2010年，Dijk等[5]利用Gentry的构造方法构造了整数上的全同态加密方案DGHV，该方案使用了成熟的困难问题，所以成为第一个被广泛认为安全的全同态方案。此后相继诞生了几个全同态加密方案[6-9]，但这些全同态加密方案实现起来都非常复杂，效率很低，并不实用。2013年，Gentry等人[10]基于LWE问题，利用近似特征值方法提出了一个新的全同态加密方案，一定程度上简化了全同态加密的实现，但与实际应用还存在不小的差距。

1984年,Shamir[11]提出了基于身份的公钥密码体制，用户公钥是与用户身份相关的可识别的一串字符，这就为加密后的数据提供了更灵活的访问控制。2001年，Cocks[12]基于二次剩余假设提出了第一个较为实用的IBE方案。随后基于身份加密方案的应用和研究广泛开展，研究人员利用椭圆曲线上的双线性对和多线性对设计出了其他的IBE方案[13-15]。2014年，Ducas等人[16]利用NTRU格上的特殊分布提出了第一个基于格的IBE方案，并将密钥和密文大小控制在2～4 kbs，使得该方案较为实用。

2013年,Clear等人[17]基于Cocks的IBE方案构造了一个具有加法同态性质的IBE方案(XOR-Homomorphic IBE)。由于该方案只实现了加法同态性质，所以并不能同时满足乘法同态的运算要求,很大程度上限制了IBE方案的功能。2014年,Clear等人[18]又提出了一个自举的全同态IBFHE方案，并能扩展应用到属性基加密(ABFHE方案)，但由于全同态的引入，不可避免的造成了计算复杂度太高。

为了实现IBE方案同态性质上的改进，同时考虑到全同态加密实现上的复杂性，本文选择了效率更高的类同态加密方案。将文献[12]中的IBE方案与文献[2]中的类同态加密方案结合，构造了一个新的具有类同态性质的IBSHE方案，分别论证了该方案能满足对密文进行任意多次加法运算和一次乘法运算，并在随机预言机模型下证明了该方案的安全性。

1　相关基础理论

1.1同态加密

同态加密方案含有四个算法：密钥生成算法(Keygen)、加密算法(Encrypt)、解密算法(Decrypt)和密文计算算法(Evaluate)。其中前三个算法提供加密和解密功能，密文计算算法是同态加密方案的核心所在，因为同态的目的就是要实现对密文的直接计算。将同态性质描述如下：

1) 生成系统参数和公私钥，Gen(1λ)→(pk,sk),∀c∈C,∀m1,…,mt∈M。

2) 运用同态加密对明文进行加密运算，得到相应密文：

∀c1,…,ct←Enc(pk,m1),…,Enc(pk,mt)

3) 密文计算算法对电路C(电路C代表一个函数或者一个功能)上输入的一组密文c=(c1,…,ci)(其中ci←encrypt(mi))进行计算。

4) 解密算法对计算后的密文解密，得到与对明文作相应运算的结果相同的解密结果：

C(m1,…,mt)=Dec(sk,Eval(pk,C,c1,…,ct))

1.2双线性映射

G、G1是由大素数p生成的循环群，p为生成元，阶都为素数p，若群G、G1中的离散对数问题均为困难问题，则所定义的双线性映射e:G×G→G1满足的性质为：

2) 非退化性存在g1,g2∈G，使得e(g1,g2)≠1。

3) 可计算性存在有效的算法使得对任意g1,g2∈G，可以计算出e(g1,g2)。

满足以上条件的双线性映射e可以利用有限域上的超奇异椭圆曲线中的Weil对或Tate对构造出来。

1.3子群判定问题

定义算法Φ，给定安全参数τ∈Z+,运行Φ(τ)生成五元组(〗q1,q2,G,G1,e)，其中群G,G1具有相同的阶n=q1q2，e:G×G→G1是双线性映射。输入τ，算法Φ运行如下：

1) 生成两个随机的τ-bits素数q1,q2，并计算n=q1q2；

2) 生成如1.2节所述具有双线性映射的群G,G1，g是群G的一个元素，且有双线性映射e:G×G→G1；

3) 输出(q1,q2,G,G1,e)。

子群判定问题是指：给定(n,G,G1,e)和一个元素x∈G，如果x的阶是q1则输出‘1’，否则输出‘0’。上述问题也可以描述为：在群的阶n的因子分解未知的情况下，判定一个元素x是否属于G的一个子群。

对于攻击算法S，解决子群判定问题的优势SD-AdvS(τ)可以定义如下：

定义1如果一个多项式时间算法S的优势SD-AdvS(τ)可忽略，则Φ满足子群判定假设。

1.4二次剩余问题

设p是一个奇素数，p不整除a，如果同余方程x2≡a(modp)有解，则称a为模p的二次剩余，否则称a为模p的二次非剩余。将二次剩余的集合记作QR(p)。

2　方案具体实现

2.1加解密算法

基于文献[12]中提出的IBE方案与文献[2]中提出的类同态加密方案的思想，本文提出了一个具有类同态性质的IBSHE方案。该方案包括四个算法：Setup,KeyGen,Encrypt,Decrypt。

Setup(1λ)→PK,MSK：算法输入安全参数λ，根据参数λ输出系统的公钥参数PK和系统的主密钥MSK。随机选择大素数p,q，使p,q满足条件p≡q≡3(mod4)，计算合数N=pq，运行1.3节给定的算法￡(λ)生成元组(p,q,G,G1,e)，其中群G、G1具有相同的阶N=pq，群G,G1满足双线性映射e:G×G→G1。在G中随机选择元素g、u，令h=uq。得到系统的公钥参数为：PK=(N,G,G1,e,g,h)。系统的主私钥为：MSK=(p,q)。

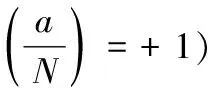
所以，最终得到的用户私钥为：SKid=(id,r,p)。

得到的密文为：ψ=(s1,s2)。

2.2同态性质分析

定义2一个同态加密方案：密钥生成算法(Keygen)、加密算法(Encrypt)、解密算法(Decrypt)和密文计算算法(Evaluate)。对于给定的电路C，任意由Keygen生成的密钥对(pk,sk)，任意t个明文m1,m2,…,mt以及经同态加密后每个明文对应的密文c1,c2,…,ct(其中ci←encrypt(mi))，如果方案满足：

Decrypt(sk,Evaluate(pk,C,c))=C(m1,m2,…,mt)

则称该同态加密方案是正确的。

本节主要是证明2.1节中提出的IBSHE方案具有类同态性质。

证明方案具有加法同态性质：系统的公钥为(n,G,G1,e,g,h)，当r2≡a(modN)时，系统对明文m1,m2∈{0,1}分别进行加密，返还给用户的密文为C1,C2∈G(其中C1=gbhe1,C2=gche2)，用户通过计算C=C1C2he3=g(b+c)h(e1+e2+e3)=g(b+c)he，进一步计算可得到：

从而论证了方案具有加法同态性质。

证明方案具有乘法同态性质：利用双线性映射的性质，我们可以实现对密文的一次乘法同态运算。令g1=e(g,g),h1=e(g,h)，g1,h1的阶分别为n,p，定义h=gαq(α∈Z)。对于两个明文加密得到密文为：C1=gbhe1∈G,C2=gche2∈G，需要对密文做如下运算使得运算结果解密后与直接对明文做乘法运算所得结果相等：

1) 随机选择e3∈Z2

2) 计算C=e(C1,C2)hr∈G1，计算过程如下：

3) 进一步计算得到：

则可以计算：

应该注意到的是，由于双线性对本身性质的限制，所以只允许对密文进行一次乘法操作，但仍可以对一次乘法操作后的密文继续进行加法操作。从而论证了方案具有一次乘法同态性质。

综合以上所述，2.1节中提出的IBSHE方案可以对密文进行一次乘法操作和任意多次加法操作，方案具有类同态性质。

3　安全性分析

3.1安全模型

IBE方案的安全模型定义如下：

1) Init：攻击者声明即将挑战的身份id*；

2) Setup：挑战者运行Setup算法并将得到的系统公钥参数发送给攻击者；

3) Key Query：攻击者请求用户id的私钥，限制是id≠id*，挑战者调用密钥生成算法并将所得私钥SK发送给攻击者；

4) Challenge：攻击者提交两条等长的密文m0和m1，攻击者随机选择一个明文并对其加密，将加密的密文发送给攻击者(攻击者可再重复进行Key Query的过程，直至攻击者认为有把握进行猜测为止)；

5) Guess：攻击者猜测挑战者加密的是哪一条明文，猜对则攻击者获胜。

在上述攻击游戏中，当且仅当攻击者获胜的概率可忽略时，才认为IBE方案是安全的。

3.2安全性证明

上述方案的安全性可用以下定理来描述

定义3一个IND-ID-CPA敌手A利用多项式时间算法在子群判定问题困难性假设下以ε的优势赢得3.1节中的游戏，当且仅当优势ε可忽略时，2.1节中构造的IBSHE方案具有IND-ID-CPA安全性。

证明我们在随机预言机模型下证明方案的安全性：

假设敌手A试图攻破本方案，A构造一个多项式时间攻击算法S用于具体实施攻击。S运行如下：

1) A选择身份id*为攻击目标，S将id*转发给C；

2) S从挑战者C那里得到公钥PK，将它传送给A；

3) S以H′(id)·h-2作为对id的哈希值(显然应有限定条件id≠id*，其中H′是S的随机预言机)，这个结果在ZN[+1]中均匀分布；

4) S根据id生成密钥K(id)·h-1，其中K是S的密钥生成模型；

5) 令a=H(id*)。敌手输出m0,m1，挑战者随机选择b∈{0,1}，将mb加密，首先计算出(c,d)，再计算c(x)=gchr∈G,d(x)=gdhr∈G(其中(c,d)是对明文b加密得到的初始密文，(c(x),d(x))是对(c,d)进一步进行同态加密得到的密文)，将(c(x),d(x))发送给攻击者A；

6) A根据所得到的信息输出b′，如果b′=b,则敌手攻击成功。

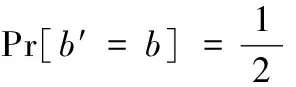
4　结　语

本文通过Cocks的IBE方案与Boneh的BGN方案相结合，构造了一个新的具有类同态性质的IBSHE方案。对方案的同态性质进行了论证并基于随机预言机模型证明了方案的安全性。接下来将继续对同态加密以及基于身份和基于属性的加密体制进行研究，进一步的工作希望可以更为深入地研究同态加密在基于身份和基于属性的加密体制中的具体应用，并构造相关的应用协议。

[1] Benaloh J.Dense probabilistic encryption[C].SAC 1994.1995:121-145.

[2] Boneh D,Goh E J,Nissim K.Evaluating 2-DNF formulas on ciphertexts[C]//LNCS.2005:325-341.

[3] Gentry C,Halevi S,Vaikuntanathan V.A simple BGN-type cryptosystem from LWE[C]//LNCS.2010:506-522.

[4] Gentry C.Fully homomorphic encryption using ideal lattices[C]//Proc.of STOC.2009:169-178.

[5] Dijk M,Gentry C,Halevi S,et al.Fully Homomorphic encryption over the integers[C]//Proc of EUROCRYPT’10,2010:24-43.

[6] Brakerski Z,Vaikuntanathan V.Fully homomorphic encryption from ring-LWE and security key dependent messages[C]//Proc. of CRYPTO’11. 2011:501.

[7] Brakerski Z,Vailuntanathany V.Efficient fully homomorphic encryption from(standard) LWE[C]//ECCC.2011:109-138.

[8] Brakerski Z,Gentry C,Vaikuntanathan V.(Leveled) fully homomorphic encryption without bootstrapping[C]//Proc of the 3rd Innovations in Theoretical Computer Science Conference,2012:309-325.

[9] Gentry C,Halevi S,Smart N P.Fully homomorphic encryption with polylog overhead[C]//Proc.of EUROCRYPT’12.2012:465-482.

[10] Gentry C,Sahai A,Waters B.Homomorphic encryption from learning with errors:conceptually-simpler,asymptotically-faster,attribute-based[C]//Proc. of CRYPTO’2013.2013:75-92.

[11] Shamir A.Identity-based cryptosystems and signature schemes[C]//Pro. of CRYPTO’84 on Advances in Cryptology,1984:47-53.

[12] Cocks C.An identity-based encryption based on quadratic residues[C]//Proc of International Conference on Cryptography and Coding,2001:360-363.

[13] Ye Zhang,Mamous N.Anonymous fuzzy identity-based encryption for similarity search[C]//Cryptology ePrint Archive,2009:496.

[14] Sharmila S,Selvi D,ScreeVivek S,et al.Identity-based online/offline encryption and signcryption schemes revisited[C]//LNCS.2011:111-127.

[15] Park S,Lee K,Lee D H.New constructions of revocable identity-based encryption from multilinear maps[OL].2013.http://eprint.iacr.org/2015/.

[16] Ducas L,Lyubashevsky V,Prest T.Efficient identity-based encryption over NTRU lattices[OL].2014.http://eprint.iacr.org/2015/.

[17] Clear M,Hughes A,Tewari H.Homomorphic encryption with access policies:characterization and new constructions[C]//Africacrypt,2013:39.

[18] Clear M,McGoldrick C.Bootstrappableidentity-basedfully homomorphic encryption[OL].2014.http://eprint.iacr.org/2015/.

CONSTRUCTION AND ANALYSIS OF THE HOMOMORPHIC IBE SCHEME OF BGN TYPE

Dai XiaomingZhang WeiZheng Zhiheng

(Key Laboratory of Information Security, Engineering University of Armed Police Force,Xi’an 710086,Shaanxi,China)

Since the identity-based public key encryption(IBE) is different from traditional public key encryption, the public key in IBE is a string of characters which is related to the identity of the user, thus it provides the encrypteddata with a more flexible access control.BGN is a homomorphic encryption scheme proposed in 2005, which is able to do arbitrary additions and one multiplication to the encrypted message, but it is not an IBE scheme still.On the basis of the BGN scheme, a new homomorphic IBSHE scheme based on quadratic residue and subgroup decisional problemis constructedto obtain a homomorphic IBE scheme which satisfies the demand of identity-based encryptionscheme in network. Also, the CPA security of the scheme is proved by random oracle model.

Homomorphic encryptionIdentity-based encryptionBilinear mapQuadratic residue problemSubgroup decisional problem

2015-10-28。国家自然科学基金项目(61272492，6110 3230)。戴晓明，硕士生，主研领域：公钥密码学。张薇，副教授。郑志恒，硕士生。

TP3

A

10.3969/j.issn.1000-386x.2016.09.072