一种新的基于混沌的彩色图像加密算法

谢国波　苏本卉

(广东工业大学计算机学院　广东 广州 510006)



一种新的基于混沌的彩色图像加密算法

谢国波苏本卉

(广东工业大学计算机学院广东 广州 510006)

提出一种使用传统的Cat映射与混沌序列结合的方法对彩色图像进行置乱扩散加密，克服了Cat映射周期性与易受选择明文攻击的缺陷。算法使用了Logistic映射和Chebychev映射。首先利用Chebychev映射的平衡性产生密钥，控制Logistic映射的参数，产生多个不同参数的Logistic序列；再用Logistic序列控制图像置乱的范围，使用Lorenz系统得到每次Arnold变换的密钥和置乱次数。置乱完成后，再使用Lorenz系统控制扩散时操作的变量。实验仿真表明：该算法对图像有比较好的置乱扩散效果，克服了Cat映射缺点，并且具有很大的密钥空间，能够高质量加密图像并抵抗常见的攻击。

置乱扩散Cat映射混沌序列控制

0　引　言

现代社会中，人们的生活与互联网的联系正日趋紧密。然而，随着互联网信息技术的快速发展，使用多媒体表达信息已经变得十分普遍。特别地，由于数字图像的直观性强、信息量大等特点使其被广泛地应用在各个行业。相应地，图像的安全性问题受到重视，怎样对图像进行安全性高的加密也成了中外学者所致力于研究的一项课题。巨大的市场需求下，多种多样的加密体制不断涌现。由于混沌系统对初始值和参数的敏感性以及后期生成的序列的混乱性正好与密码学中的某些原则极其相似，学者们开始设想把混沌应用于加密技术，并提出了一系列混沌加密算法[1]。

对图像的混沌加密主要是借助混沌映射生成混沌序列，对图像进行置乱和扩散。而置乱过程中一个经典的置乱技术就是使用Cat映射的Arnold变换。Arnold变换具有周期性，简单的Arnold变换很容易被选择明文攻击破解。为了克服这一点，本文算法采用对图像不同范围进行置乱的方法，用大范围的置乱改变小范围的的置乱结果。小范围的置乱干扰大范围的置乱，打破了Cat映射的周期性，很好地隐藏了原始图像。

1　Cat映射与混沌系统介绍

1.1Cat映射

Cat映射的表达式如下：

该方程可写为：

根据映射公式很容易发现其产生密图的两个因素：拉伸和折叠。映射中点坐标值通过与矩阵相乘使得坐标变大，这相当于拉伸；而取模运算使其缩小到了单位矩阵内部，这相当于折叠。

Cat映射具有周期性，即经过若干次变换后，矩阵会回到最初状态，且周期T与N的大小有关。

1.2混沌系统的介绍

本文涉及到的混沌系统有三种：Logistic映射、Chebychev映射以及Lorenz系统。

(1) 一维Logistic映射关系表达式如下：

xn+1=μxn(1-xn)n∈{1,2,…}

该序列产生的值x∈[0,1]。当0<μ≤1时，不论以何值作为初值，经过多次迭代后，其序列值最终趋近于0。当1<μ≤3时，序列经过多次迭代后会趋近于0或1-1/μ。当3<μ≤4时，序列多次迭代将进入混沌状态，其产生的序列值处于伪随机状态。μ值越接近4，系统的混沌性越强。

(2) k阶的Chebychev映射可用以下公式表示：

xn+1=cos(k×arccos(xn))

当参数k=6时，Chebychev系统的Lyapunov指数为1.791733……，映射处于混沌状态。 Chebychev系统对于初始状态具有强烈的敏感依赖性。

(3) Lorenz系统可表示为如下方程：

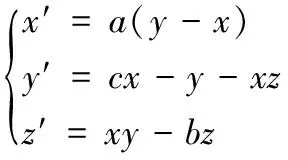
当a=10、c=28、b=8/3时，系统处于混沌状态。

2　算法分析与设计

2.1加密步骤及分析

图像的加密过程一般包含两个步骤：置乱和扩散。置乱时，我们使用Cat映射从图片的中心位置开始置乱，随后慢慢向四周扩大置乱范围，最后进行最外层置乱，即对整体置乱。利用这样层层向外扩展的置乱，能够使得一层的置乱打乱另一层置乱的结果，使得Cat映射的周期性被打破。置乱时由混沌映射得到每次置乱的最外围的置乱层数，即置乱的范围。置乱的次数由图像本身获得。

图像的置乱包含两个层次的置乱，大的置乱和大置乱中的不同范围的置乱。每个大的置乱至少需要对图像小置乱三次，即每次大的置乱至少对图像进行三次不同范围的置乱。置乱顺序从里到外，包括最里层置乱、中间范围置乱和最外层置乱。其中每次大的置乱中最外层置乱和最里层置乱均运行一次，中间范围置乱至少一次，最大不会超过图像长的二分之一。

每次Arnold变换的密钥和次数由Lorenz系统控制，每小范围置乱一次图像就更换Arnold变换的密钥和次数。

由于Arnold变换适用于长宽相等的图像，所以为了方便本实验使用的图片是大小为256×256 的Lena彩色图像。对于长宽不等的图像可使用一系列算法进行填充，然后使用本算法进行加密。本算法的外部密钥：key1、key2、x1、x2、x、y、z、K。

2.1.1图像置乱步骤

Step1把图像读取成一维数组C,其中每个像素点的分量值按序存储。使用原始图形所有颜色分量和sum和长度N经式(1)计算出置乱次数K1：

K1=mod(sum,256)+N

(1)

Step2由明文密钥key1作为Chebychev的参数，x1作为初始值x0进行Chebychev映射的迭代。舍弃前100次迭代的值，从101次起再迭代K1次，产生K1个值并保存到序列X中。由于Chebychev迭代出的值的范围为[-1，1]，对序列X进行正数化：对于负数取其绝对值,对于值为0的数，用0.1代替。然后对序列中值进行从小到大排序产生序列L。

Step3对L序列进行式(2)变换，变换后的值按顺序赋给LX序列。

LX[i]=(L[i]×0.3)+3.7

(2)

Step4以key2、x2作为Chebychev参数和初始值，重复步骤Step2，得到序列LY。

Step5以当前加密的次数为下标，若当前是第n次加密，则以LX序列的第n个值作为Logistic映射参数，LY序列第n个的值作为映射初始值进行迭代。舍弃前100个值，把得到的第101个值x0进行式(3)变换得到本次大置乱中中间的范围置乱次数k0，若x0为0，则k0为1。

k0=mod(x0×1014，floor(N/2))

(3)

Step6然后以x0作为初始值继续迭代k0次得到序列T,把序列T中的值进行式(4)变换后从小到大排序得到序列T′。

T′=mod(T[i]×1014，floor(N/2))

(4)

Step7由外部密钥x、y、z作为Lorenz系统的初始值进行迭代，得到值x′、y′、z′。把x′、y′、z′进行式(5)变换得到Arnold变换的密钥key1、key2以及使用该变换的加密次数k′。下一次的Arnold变换的密钥和置乱次数由x′、y′、z′作为Lorenz系统的初始值迭代得出，依次类推。

(5)

Step8若最外层为第1层的话，则最内层为第floor(N/2)层。 首先对最内层也就是第floor(N/2)层范围内的图像进行置乱，然后依次对第floor(N/2)+T′[i] (0≤i≤k0)层范围内元素进行置乱，最后对第一层内元素也就是整个图像进行置乱。置乱完成后即是一次大的置乱。置乱实例如图1所示。

图1　一次大的置乱步骤与效果图

Step9重复步骤Step5-Step8 K次后得到置乱序列C。

2.1.2图像扩散步骤

Step1由外部密钥x、y、z作为Lorenz系统的初始值进行迭代，丢弃前100次迭代生成的值。然后再迭代N2次生成序列EX、EY、EZ，把这三个序列进行式(6)变换得到FX、FY、FZ。则(FX[i],FY[i],FZ[i])包含27种情况，分别映射不同的分量，如表1所示。

(6)

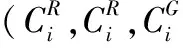
(7)

Step3重复上述步骤K次得到加密序列，然后把序列恢复成的图像就是密图。

2.2解密步骤及分析

解密过程即是加密的逆过程，按照加密的逆顺序先对像素点使用式(8)异或解密成序列C，然后对C进行反置乱还原成初始序列。

(8)

对置乱序列进行还原时，首先需要计算出每个大置乱中小置乱的次数，得到小置乱的总次数，然后迭代Lorenz序列同样多次，逆向进行反置乱操作。

图像的加密和解密流程如图2、图3所示。

图2　图像加密流程图

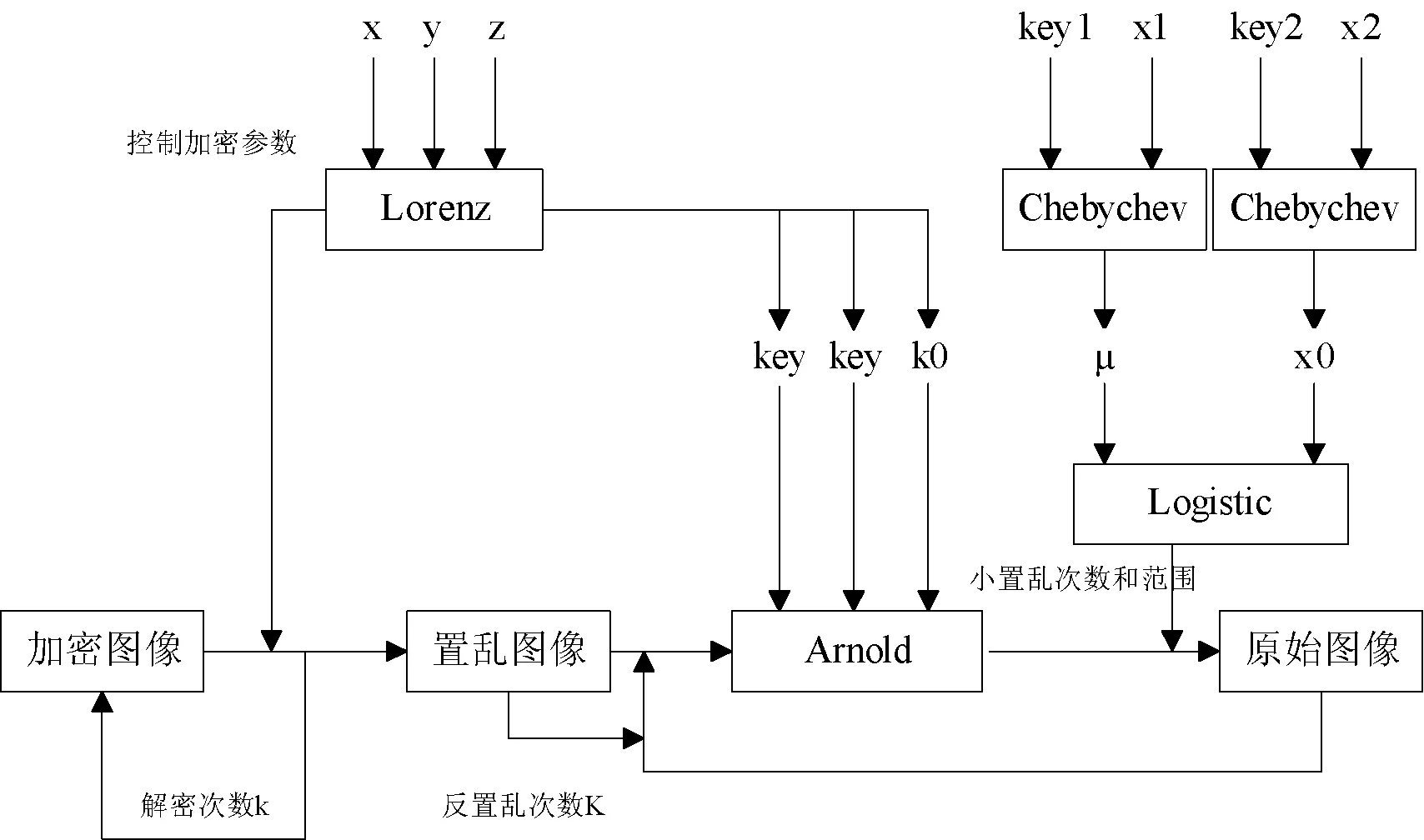
图3　图像解密流程图

3　算法仿真分析

加密算法是否能够抵御来自破解者的攻击主要依靠算法的密钥空间以及对密图的仿真数据结果的分析来得出。加密攻击有四个级别：唯密文攻击、已知明文攻击、选择明文攻击、选择密文攻击。本次加密图像仿真针对常见的图像攻击分析方法：已知、选择明文攻击常用的统计分析，唯密文攻击常用的穷举分析以及选择明文攻击常用的差分能力来进行举证。

3.1实验数据及结果

本实验用到的密钥数据是：key1=0.35845654，key2=0.39999999，x1=x2=0.34567,x=y=z=9.9999999。图4是原始图像和对应的置乱图像与置乱扩散图像。

图4　图像置乱扩散效果图

3.2密钥空间的大小

本算法用到的密钥有key1、key2、x1、x2、x、y、z、K。本算法测试表明，对任何一个密钥(除K外)，将其改变10-14大小均不能正确解密图像，所以若除K外每个密钥均有14位有效数字，则密钥空间大于1014×7=1098>2100。这表明以穷举法来对密图进行破解几乎没有可能，即本算法有足够大的密钥空间来抵抗穷举攻击。

3.3信息熵分析

信息熵可以描述判断元素的随机性，公式如下：

其中，p(si)表示si的概率。对于一个具有2T种可能性的序列来说，若该序列是随机的，则它的信息熵应该无限趋近于T，随机性越强，越接近T。当我们测试一幅彩色图像加密后的图像时，可以分析图像中每个分量的信息熵。因为每个分量具有28可能性，所以只需看其值是不是趋近于8即可。通过计算我们给出原始图像和加密后的图像的信息熵如表2所示。

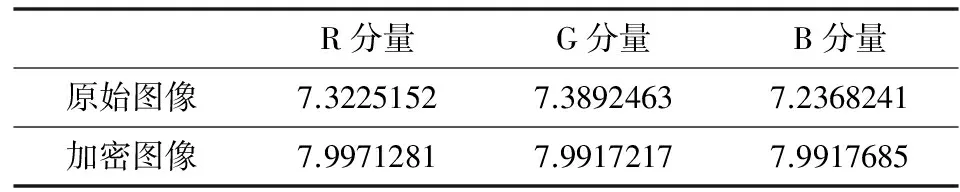
表2　原始图像与加密图像信息熵

由表中我们可以看出，加密后的图像信息熵均接近8,所以证明经本算法加密后，密图中各像素点分量值具有很强的随机性。

3.4直方图分析

原始图像和加密图像(一次加密)的各颜色分量直方图如图5所示。图中看出原始图像中各分量是不均衡的，加密后的图像中各分量非常均衡，这表明各分量在加密后取值均等，即加密后图像很好地掩盖了原始图像的信息，能够有效地防止统计分析攻击。

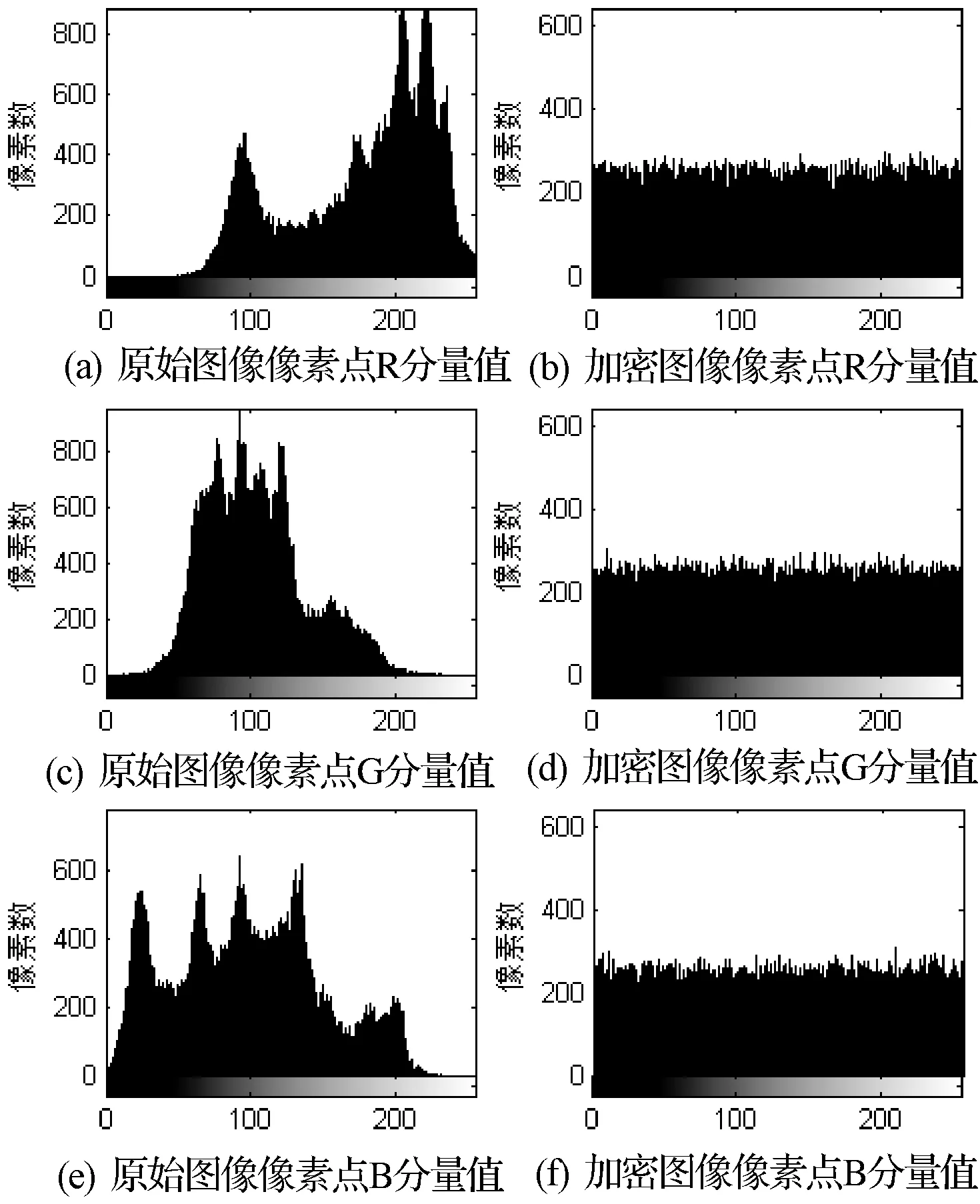
图5　原始图像和加密图像直方图

3.5相邻像素相关性

为了判断密图的杂乱性，我们对原始图像和加密图像分别从水平、垂直和对角方向随机选取1000组元素进行分析统计，对图像分析需要用到下列用于相关性分析的公式，其中xi和yi分别表示随机选取的坐标点的颜色分量值和与之相邻(水平相邻、垂直相邻、对角相邻)的点的颜色分量值。

经过对原始图像一次、两次加密的图像进行计算后给出的各分量的相关系数如表3所示。

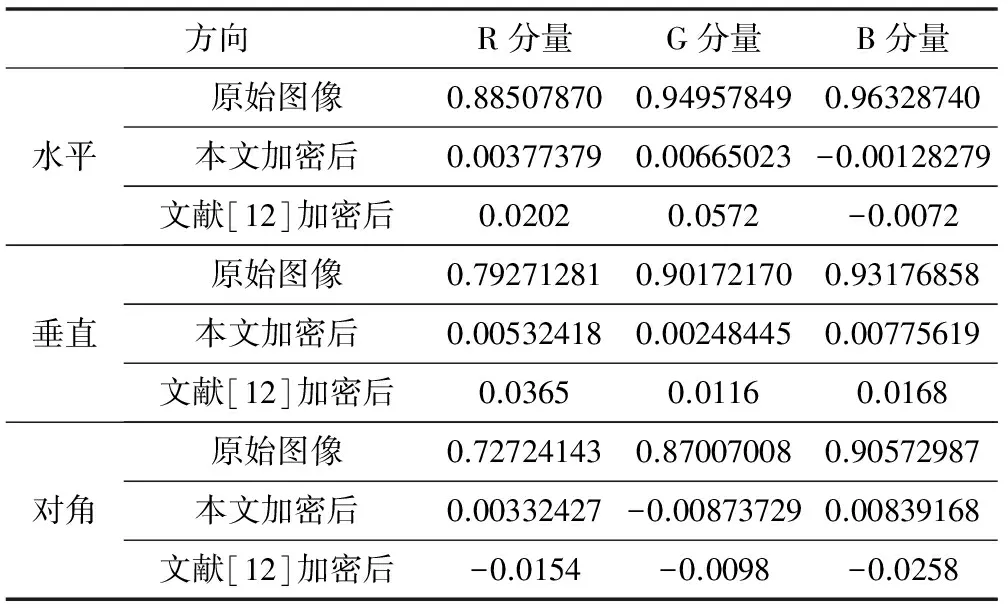
表3　加密前后图像相邻像素值的相关性

由于计算机随机函数的伪随机性，为保证实验结果的准确性，以上表中数据均为第一次随机运算得出。

由表中数据的分布可以看出，无论从水平、垂直还是对角方向来看，原始图像相邻像素的相关性系数比较大，均接近于1。而经过本文提供的加密算法加密后的密文图像相邻像素点的各颜色分量的相关系数均接近于0，密图的相邻像素已基本不相关，这说明密图中已经掩盖了原始图像的数据特征。

3.6抗差分攻击能力分析

算法对明文的敏感性越强，则其算法抗差分攻击能力就越强。我们使用NPCR (Numberof Pixels Change Rate)指标，也就是像素数改变率来衡量算法对明文的敏感性；也可以用归一化像素值平均改变强度指标UACI(Unified Average Changing Intensity)测试敏感性。我们对图像的每个像素值进行过in测量，当两个明文图像仅存在其中一个像素点的颜色分量不同时，设它们的密文图像中第(i，j)点的像素点，该分量值分别为c1(i，j)和c2(i，j)。若c1(i，j)=c2(i，j)，定义D(i，j)=0；若c1(i，j)≠c2(i，j)，定义D(i，j)=1，则NPCR与UACI的计算公式分别为:

在本测试中使用100组不同的lena图像进行加密，每组中包括一个原始图像和一个随机像素点的值为0的原始图像[11]。测试结果如表4所示，由表可以看出各分量的UACI均超过0.33， NPCR均超过0.99。由此可知本文算法对明文的敏感性极强，对于小小的变化，加密或者解密后的图像是完全不同的。

表4　NPCR与UACI度量数据

4　结　语

本文提出了一种基于混沌利用Cat映射对图像不同范围的元素进行置乱的方法，有效克服了Cat映射周期性与易受选择明文攻击的不足。该方法在加密过程中使用图像本身的特性产生加密参数，使得加密步骤与图像本身紧密相连，能够使得攻击者不可以使用脱离图像的单独策略进行破解。仿真表明了本文算法具有非常大的密钥空间，对图像置乱扩散的效果也非常好，能抵御常见的攻击。所以，本文算法具备实际的应用价值。

[1] 左飞.数字图像处理技术详解与Visual C++实践[M].北京:电子工业出版社,2014:478-518.

[2] Liu H J,Wang X Y.Color Image Encryption Based on One-time Keys and Robust Chaotic Maps[J].Computers and Mathematics with Applications,2010,59(10):3320-3327.

[3] Wang X Y,Xu D H.Image encryption using genetic operators and intertwining logistic map[J].Nonlinear Dynamics,2014,78(4):2975-2984.

[4] 谢涛,何兴.一种新的基于混沌的彩色图像加密方案[J].计算机应用研究,2013,30(1):318-320.

[5] Zhang Y S,Xiao D.Double optical image encryption using discrete Chirikov standard map and chaos-based fractional random transform[J].Optics and Lasers in Engineering,2013,51(4):472-480.

[6] Li J H,Liu H.Color image encryption based on advanced encryption standard algorithm with two-dimensional chaotic map[J].Information Security,2013,7(4):265-270.

[7] 孔涛,张亶.Arnold反变换的一种新算法[J].软件学报,2004,15(10):1558-1564.

[8] Joshi M,Shakher C,Singh K.Image Encryption Using Radial Hilbert Transform Filter Bank as an Additional Key in the Modified Double Random Fractional Fourier Encoding Architecture[J].Optics and Lasers in Engineering,2010,48(5):605-615.

[9] 张翌维,王育民,沈绪榜.基于混沌映射的一种交替结构图像加密算法[J].中国科学(E辑:信息科学),2007,37(2):183-190.

[10] Zhang Y Q,Wang X Y.Spatiotemporal chaos in Arnold coupled logistic map lattice[J].Nonlinear Analysis-Modelling And Control,2013,4(4):526-541.

[11] 蒋君莉,张雪锋.基于多混沌系统的彩色图像加密方法[J].计算机应用研究,2014,31(10):3131-3136.

[12] Liu H,Nan H.Color image security system using chaos-based cyclic shift and multiple-order discrete fractional cosine transform[J].Optics and Laser Technology,2013,50(2):1-7.

A NEW CHAOTIC-BASED COLOUR IMAGE ENCRYPTION ALGORITHM

Xie GuoboSu Benhui

(College of Computer,Guangdong University of Technology,Guangzhou 510006,Guangdong,China)

We propose the use of a method to encrypt the colour image with scrambling diffusion which combines the traditional cat mapping and the chaotic sequence, the method overcomes the defects of cat mapping in periodicity and being vulnerable to chosen-plaintext attack. The algorithm uses the Logistic mapping and the Chebychev mapping. First, it uses the equilibrium of Chebychev mapping to generate the key which controls the parameter of Logistic mapping, and generates a variety of Logistic sequence with different parameters, then it uses the Logistic sequence to control the range of image scrambling, and employs Lorenz system to get the key and the scrambling times of every Arnold transform. When the scrambling is completed, the algorithm uses Lorenz system again to control the operation variables which are used in diffusion. Experimental simulations indicate that the algorithm has better scrambling diffusion effect on the image, and overcomes the shortcoming of cat mapping, it brings large key space, and can encrypt the image with high quality as well as resist common attacks.

Scrambling diffusionCat mapChaotic sequenceControl

2015-02-08。广东省重大科技专项(2012A080103010)；广东省科技计划项目(2013B022200004，2013B090600035)。谢国波，教授，主研领域：混沌保密通信，云计算，云存储相关底层架构。苏本卉，硕士生。

TP309.7

A

10.3969/j.issn.1000-386x.2016.09.075