基于密度进化算法的正则LDPC码噪声门限

尹晓琦

(淮阴工学院电子信息工程学院，江苏淮安　223003)



基于密度进化算法的正则LDPC码噪声门限

尹晓琦

(淮阴工学院电子信息工程学院，江苏淮安223003)

针对LDPC码(低密度奇偶校验码)的噪声门限问题，基于置信传播算法讨论密度进化算法的实现方法，通过对校验节点均值迭代公式的简化来确定门限值，简化算法降低了迭代运算的复杂度，减小了运算量.构造了3种不同次数分布的LDPC码，对其在高斯白噪声信道下噪声方差门限和信噪比门限进行了理论计算和仿真，并对结果进行了比较分析.研究结果表明，随着列重的增加，LDPC码的误码性能将变差，选择好的次数分布能获得优秀的误码性能，这对LDPC码进一步的应用研究具有指导意义.

LDPC码；译码；密度进化；噪声门限

低密度奇偶校验码(low-density-parity-checkcodes，LDPC)是一种逼近香农限的线性分组码，码率为1/2的LDPC码在BPSK调制方式下的误码性能距香农限仅有0.045dB，是目前距离香农限最近的信道编码[1-2]，它利用监督矩阵的低密度特性，降低了译码的复杂度，提高了解码速度，由于其具有类似随机编码的特征，所以拥有优秀的编码性能.Gallager对LDPC码在二进制对称信道中的译码特性进行了研究，发现LDPC码在译码的过程中存在门限问题[3].当LDPC码的码长增加时，只要信道的噪声功率比噪声门限值低，通过置信传播算法对LDPC码进行译码，仍然能获得较好的误码性能；而当噪声功率比门限值高时，LDPC码的误码率则无法达到理想状态，而是大于某个正的常数.Richardson和Urbanke定义了这个译码门限[4]，并且提出了密度进化的直接算法，但是这种方法的计算量太大.Elsa等在设计非二进制LDPC码时，对非二进制对称信道的密度进化算法进行了优化，通过对有限长度编码的渐进性能仿真获得了编码的优化度分布[5].陈紫强等[6]研究了高斯白噪声信道下联合LDPC码的密度进化算法，结合译码收敛条件和度分布约束关系，提出联合LDPC码的度分布优化问题.由于在AWGN信道中迭代运算的信息分布是相近的，因此在密度进化过程中消息的概率密度为近似高斯分布.本文基于高斯近似方法讨论LDPC码密度进化算法的实现方法，通过对节点之间消息密度迭代运算的简化来确定噪声门限值.

1　LDPC码的Tanner图

LDPC码作为一种线性分组码，可以用监督矩阵的形式来表示，也可以用Tanner图来描述.Tanner图包括变量节点和校验节点2个集合[7]，检验节点对应监督矩阵的行，变量节点对应监督矩阵的列，集合内部的各节点之间没有连线，而不同集合的各节点之间可能有连线，ci与vj相连表示矩阵中第i行、第j列的元素为1.例如一个(6,2,3)正则LDPC码的Tanner图(如图1所示)，图中4个变量节点构成集合{v1,v2,v3,v4}，6个校验节点构成集合{c1,c2,…，c6}，2个集合内部没有连线，但集合之间根据校验矩阵中“1”的分布来连线，其中，H1,1=1表示c1与v1相连.另外，图论中定义与某个节点x相连的边数为节点次数deg(x).在图1的Tanner图中，变量节点vi的节点次数deg(vi)为3，校验节点cj的节点次数deg(cj)为2.

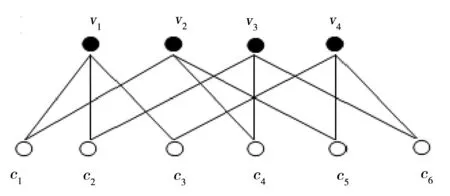
图1　(6,2,3) LDPC码Tanner图Fig.1　Tanner figure of (6,2,3) LDPC codes

2　基于置信传播算法的密度进化算法

2.1置信传播算法(BP算法)

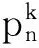
定义

(1)

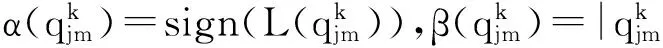
定义

(2)

置信传播算法步骤如下：

(3)

2)判断迭代次数k是否大于设定值，如果成立，则结束译码，否则继续；

3)更新校验节点cm传递给vi的对数似然比

(4)

4)计算变量节点vn的对数似然比

(5)

5)更新变量节点vn传递给cj的对数似然比

(6)

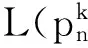
2.2密度进化算法

在BP算法中，如果是高斯白噪声信道，则信息迭代的对数似然比L(q)、L(r)服从近似高斯分布，所以迭代时可通过均值μ、方差σ2得到节点信息的概率密度f(x)，节点之间信息迭代可简化为

(7)

(8)

其中，dv和dc分别为变量节点和校验节点的最大度数.

利用节点概率密度的对称条件f(x)=f(-x)ex，对数似然比信息服从N(μ,2μ)的高斯分布，则方差μ=2/σ2，此时由均值μ就可以确定消息的概率密度.

假设LDPC码的Tanner图中没有闭合环路，信息未被重复更新，则可认为不同节点之间的对数似然比是独立同分布的.定义

(9)

(10)

根据式(7)和(8)，推导节点之间对数似然比的数学期望的迭代式为

(11)

(12)

(13)

对于式(11)可推导如下

(14)

定义

(15)

(16)

Sae[9]给出了φ(x)的上界和下界的近似表达式

(17)

φ(x)在x不是很大的情况下，可以进一步简化计算为

(18)

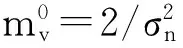
3　密度进化算法的门限与仿真结果的比较

为了进行计算机仿真运算，对算法中的变量节点和校验节点的对数似然比信息进行量化处理.设量化间隔为δ，量化比特为m，量化范围为[-N,N]，N=2m-1-1.如果对数似然比信息是在以nδ为中点的量化区间里，则量化值为n；当n<-N时，量化值为-N；当n>N时，量化值为N.

对于码长为504、码率为1/2的LDPC码，分别构造次数分布为(3,6)、(4,8)和(5,10)的正则码，量化比特为12，利用密度进化算法分别计算噪声方差门限σ2和信噪比门限SNR，结果见表1.

表1　不同次数分布正则码的门限值Tab.1　Thresholds of different drgree distribution regular codes

由表1可以看出，采用了密度进化算法简化运算后的噪声方差门限要略小于简化前的门限值，次数分布为(3,6)的LDPC码的噪声方差门限值大于次数分布为(4,8)、(5,10)的门限值，而信噪比门限中(3,6)码的值最小，但与香农限都还有一定距离.当最大迭代次数设为50时，3种次数分布的LDPC码在BP算法下的误码率性能仿真结果见图2，算法简化前后平均迭代次数的统计见图3.

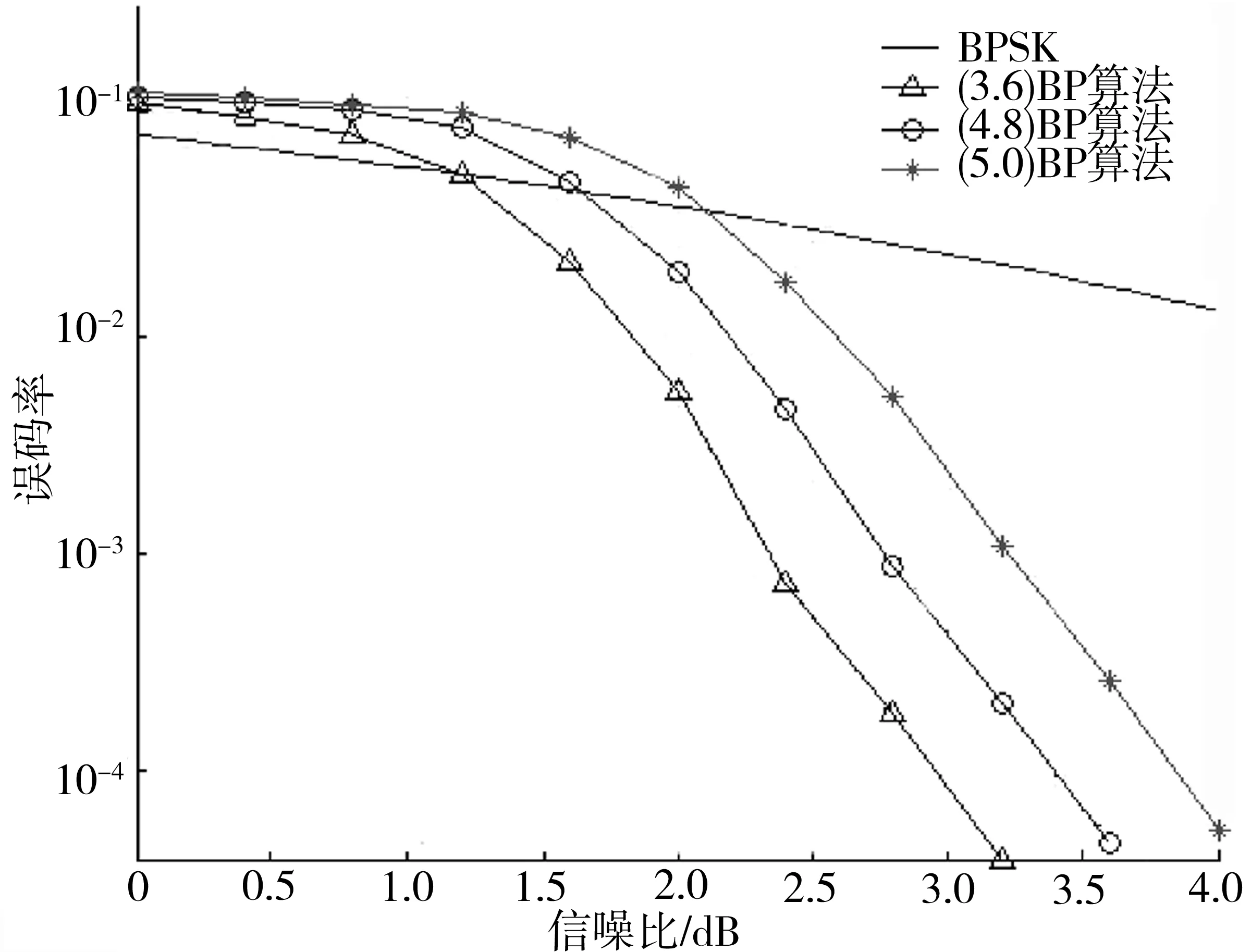
图2　不同次数分布正则码误码率性能Fig.2　Error performance of different degree distribution regular codes

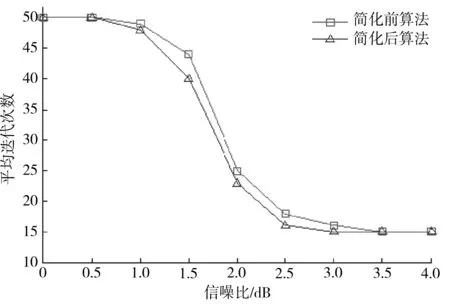
图3　平均迭代次数的统计Fig.3　Statistics of mean iteration times

由图2可知，次数分布为(3,6)的正则LDPC码的误码性能最好，而次数分布为(5,10)的性能最差，与密度进化算法迭代计算的结果一致，说明随着列重的增加，LDPC码的误码性能会变差.在误码率为10-4时，(3,6)、(4,8)和(5,10)的正则码对应的信噪比分别约为2.95、3.40和3.83dB，信噪比差值为0.45、0.43dB；而由表1的结果得到的信噪比差值为0.44、0.42dB，与仿真结果中的信噪比差值近似相等.

由图3可以看出，算法简化后的平均迭代次数逼近简化前，而从迭代运算复杂度来看，当对变量节点和校验节点的对数似然比信息进行迭代更新时,简化算法将双曲正切函数与指数函数乘积的积分运算简化为指数运算，大大减少了译码的运算量，降低了译码的复杂度.另外，误码率性能仿真结果与用密度进化算法迭代计算的结果都不是离香农限很近，这是因为所用的LDPC码的长度不是足够大，相应的监督矩阵中“1”不是足够稀疏的，且列重增加也会进一步降低校验矩阵的稀疏性，导致编码的Tanner图中出现大量的短环，使得置信传播算法的误码性能下降.

4　结论

LDPC码是一种逼近香农限的高效纠错编码，但是在译码过程中存在门限问题.本文主要讨论了一种基于置信传播算法的密度进化算法,能够通过对消息密度的迭代运算来确定噪声门限和信噪比门限的值，为LDPC码寻找最优的次数分布对提供了方法，这对LDPC码进一步的应用研究具有指导意义.

[1]MCKAYDJC.Gooderror-correctingcodesbasedonverysparsematrices[J].IEEETransInformTheory,1999,45(3):399-431.DOI:10.1109/18.748992.

[2]王兰勋,王贵贵,尹超,等.基于HMM信源估计和LDPC的联合信源信道译码[J].河北大学学报(自然科学版),2008,28(2)：209-213.

WANGLanxun，WANGGuigui，YINChao，etal.Jointsource-channeldecodingbasedonHMMandLDPC[J].JournalofHebeiUniversity(NaturalScienceEdition),2008,28(2)：209-213.

[3]GALLAGERRG.Low-densityparity-checkcodes[D].Cambridge,MA:MITPress,1963.DOI:10.1109/TIT.1962.1057683.

[4]RICHARDSONTJ,URBANKER.Thecapacityoflow-densityparitycheckcodesundermessagepassingdecoding[J].IEEETransInformTheory,2001,47(2):599-618.DOI:10.1109/18.910577.

[5]DUPRAZELSA,SAVINV,KIEFFERM,etal.Densityevolutionforthedesignofnon-binarylowdensityparitycheckcodesforSlepian-Wolfcoding[J].IEEETransactionsonCommunications,2015,63(1):25-36.DOI:10.1109/TCOMM.2014.2382126.

[6]陈紫强,欧阳缮,肖海林,等.半双工中继信道下联合LDPC码设计[J].通信学报,2013,34(3):134-140.DOI:10.3969/j.issn.1000-436x.2013.03.017.

CHENZiqiang,OUYANGShan,XIAOHailin,etal.JointedLDPCcodesdesignforhalf-duplexrelaychannels[J].JournalonCommunications,2013,34(3):134-140.DOI:10.3969/j.issn.1000-436x.2013.03.017.

[7]TANNERRM,SRIDHARAD,SRIDHARANA,etal.LDPCblockandconvolutionalcodesbasedoncirculantmatrices[J].IEEETransactionsonInformationTheory,2004,50(12):2966-2984.DOI:10.1109/TIT.2004.838370.

[8]PEARLJ.Probabilisticreasoninginintelligentsystems:networksofplausibleinference[M].SanFrancisco,CA,USA:MorganKaufmannPublishersInc,1988:552.

[9]CHUNGSY,RICHARDSONTJ,URBANKER.Analysisofsum-productdecodingoflow-densityparity-checkcodesusingagaussianapproximation[J].IEEETransactionsonInformationTheory,2001,47(2):657-670.DOI:10.1109/18.910580.

(责任编辑：王兰英)

ThresholdsofregularLDPCcodesbasedondensityevolutionalgorithm

YINXiaoqi

(FacultyofElectronicInformationEngineering，HuaiyinInstituteofTechnology，Huai’an223003,China)

TodealwiththenoisethresholdsofLDPCcodes,thedensityevolutionaryalgorithmbasedonbeliefpropagationalgorithmisdiscussedtodeterminethethresholdsthroughsimplifyingthemessageiterativearithmeticonthemeansofthechecknodeswhichcanreducethecomputingcomplexityandtheamountofcomputation.ThreedifferentdegreedistributionLDPCcodeshavebeenconstructed,andthetheoreticalcalculationandsimulationhavebeencarriedontodeterminethenoisevariancethresholdsandtheSNRthresholdsunderAWGNchannel,theresultshavebeencompared.Itshowsthatwiththeincreaseofthecolumnweight,theperformanceofLDPCcodesbecomesworse.Excellentperformancecanbeobtainedifwechoosegoodnumbersofdegreedistribution,thathasguidingsignificanceforfurtherapplicationresearchofLDPCcodes.

LDPCcodes；decoding；densityevolution；noisethresholds

10.3969/j.issn.1000-1565.2016.03.018

2015-06-12

国家星火科技计划项目(2012GA690304)；淮安市科技支撑计划项目(HAS2012046)

尹晓琦(1975-)，女，江苏淮安人，淮阴工学院副教授，主要从事无线通信与信号处理研究.

E-mail:kittyyin@hyit.edu.cn

TN

A