带有logistic源的生物趋化模型解的全局有界性

李 丹，穆春来

（重庆大学　数学与统计学院，重庆 401331）

带有logistic源的生物趋化模型解的全局有界性

李 丹，穆春来

（重庆大学数学与统计学院，重庆 401331）

研究了一个关于两个物种趋化模型的初边值问题

其中Ω⊂Rn（n≥1）是边界光滑的有界区域，χi（w）（i=1，2）为趋化敏感函数且满足，初值 u0，v0∈C0（）和w0∈W1，∞（Ω）且，αi，μ1和μ2为正，δi＞1。则当参数和μ1+μ2满足一定条件时，表明此模型的初边值问题有唯一的经典解且一致有界。

趋化性；全局有界；logistic源

0 引 言

在自然界中，所有生命体的生存都依赖于其在复杂环境中组织和处理各种内部及外部信息的能力。例如，好氧细菌会朝着氧气浓度高的地方游去，细菌会远离苯酚以免被杀死等等。此现象为趋化行为，是生物的本能反应。在1970年，Keller和Segel在文献［1］中首次提出了趋化模型，该模型是为了研究基网柄菌的黏菌的聚合现象。在最近几十年引起了广大生物学家和数学家的关注，相应地也做了很多结果。一个典型的模型如下

其中Ω⊂Rn是一个有界光滑区域，u=u（x，t）代表细胞的密度，v=v（x，t）代表化学信号物质的浓度，χ∈R代表趋化敏感度系数，△u和△v分别代表细胞自扩散项和化学物质的自扩散，-χ▽·（u▽v）代表趋化敏感度项，表示在区域边界∂Ω的外法方向上的方向导数。在数学领域中模型解的适定性、渐进行为、爆破成为了研究的重点。当n=1时，Yagi和Osaki在文献［2］中证明了模型（1）对任意充分光滑的初值是整体存在且有界的。当n=2时，有条件‖u0‖L1（Ω）＜4π成立时，Nagai在文献［3］中证明了模型的非径向对称解无解。当n≥3时，W inkler［4］证明了对任意的δ＞0，存在ε＞0使得有条件和‖▽v0‖Ln+δ（Ω）＜ε成立，则模型的解都存在且一致有界。然而，在最近，此结果得到了进一步地发展，Cao在文献［5］中证明了如果条件和‖v0‖Ln（Ω）＜ε成立，则解整体有界。W ink ler在文献［6］中通过构造 Lyapunov泛函证明了解在有限时刻爆破。

以上模型考虑的是化学物质由细胞产生而非消耗，接下来的模型考虑的是一种化学信号物质被消耗的情况

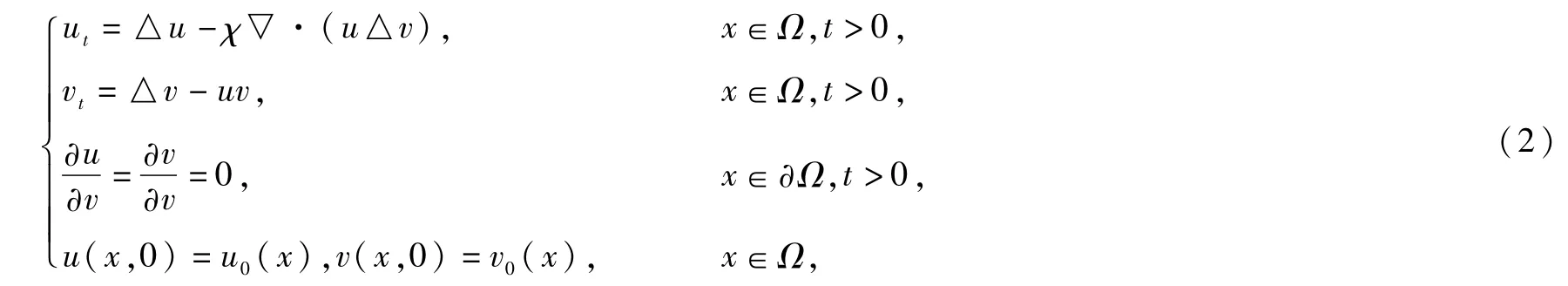
其中u=u（x，t）代表细胞的密度，v=v（x，t）代表的是氧气的浓度。当n≥2时，Tao在文献［7］中通过构造权函数证明了当‖v0（x）‖L∞（Ω）充分小时，模型的解整体存在且一致有界。当n=3时，Tao和W inkler证明了模型（2）解的渐进行为。然而，以下关于两种生物的趋化模型最近也有了些进展

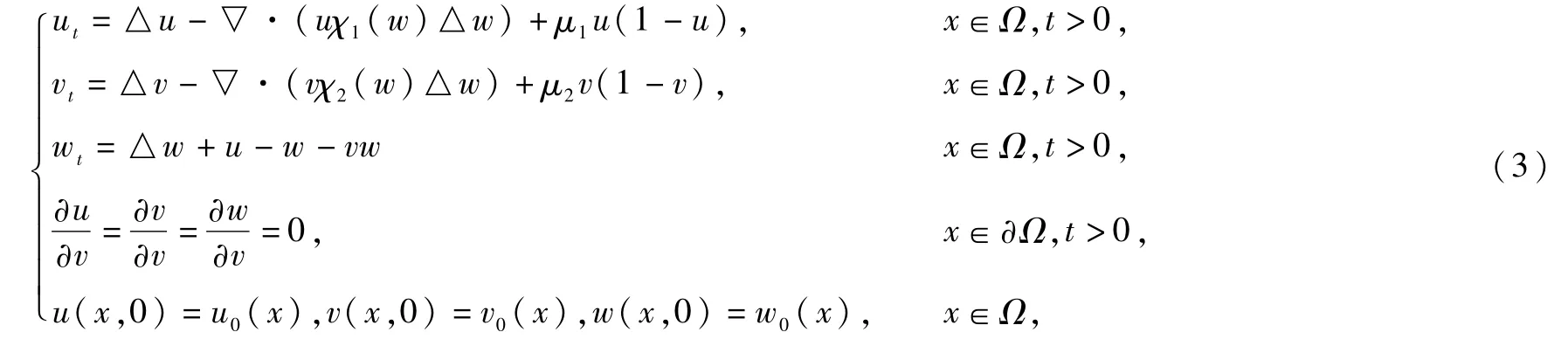
其中u（x，t）和v（x，t）分别代表两个物种的密度，w（x，t）代表化学信号的浓度。同样地，Ω⊂Rn是一个有界光滑区域，此模型表示化学物质w（x，t）被物种v（x，t）消耗而不被u（x，t）消耗。特别地，Li在文献［8］中研究了模型（3）不带logistic源的情况（即μ1=μ2=0），得到了在二维情况下的全局有界性且在条件‖u0‖L1（Ω）＜ε和‖▽w0‖L1（Ω）＜ε（ε充分小）下，当t→∞ 时模型（3）的解（u，v，w）趋于稳态解（z1，z2，），其中。在此文章中，我们对一般的情况进行了研究。为了简化问题，首

先令m∶=u+v，由模型（3）直接计算可得

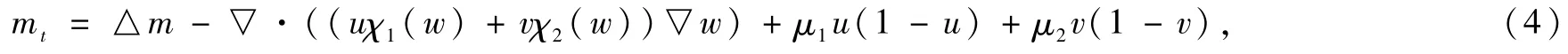
其中对所有的 w≥0和 χi∈C1+δi（［0，∞］）趋化敏感函数χi（w）满足

定理1 假设Ω⊂Rn是一个有界光滑区域，初始值（u0，v0，w0）满足（6）且趋化敏感函数χi（w）满足（5），则当参数，i=1，2和μ1+μ2分别满足和时，模型（3）有唯一经典解且关于时间是一致有界的，其中

论文安排如下：在下面一节中将主要给出一些相关引理；主要结果定理1的证明在第三部分，首先证明u（x，t）在空间L2（n+1）（Ω）上是有界的，最后利用Moser迭代法得到定理1。

1 预备知识

为了证明定理1，我们先给出一些相关的引理。

引理 1 假设非负初值（u0，v0，w0）满足（6），Ω⊂Rn（n≥1）是一个有界且具有光滑边界∂Ω的区域。则存在Tmax∈［0，∞）和非负函数（u，v，w）满足

证明 模型（3）经典解的局部存在可利用不动点定理得到，详见文献［9-11］。

引理2［12］取z（t）≥0满足

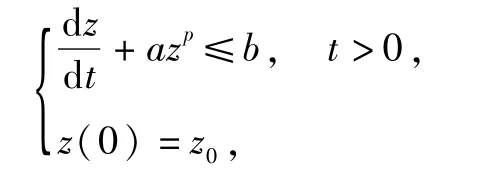
其中常数a＞0，p＞0，b＞0，则我们有

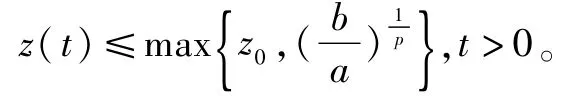
引理3 假设（6）成立，则模型（1）的解（u，v，w）满足

证明对模型（3）中的第一个方程在Ω上积分，我们得到

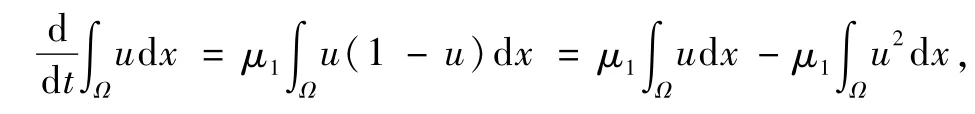
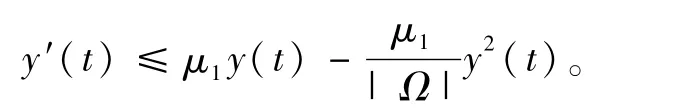
和

根据常微分方程比较原理可以得到结果。

接下来，我们将引进一个有用的不等式，详见参考文献［3，11，13-14］。

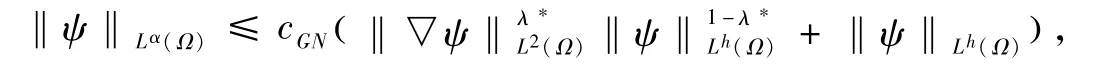
其中ψ∈W1，2（Ω）且

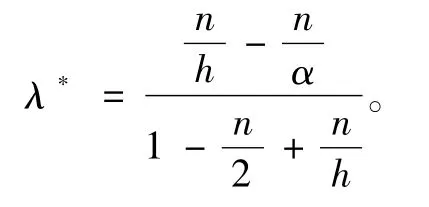
2 定理1的证明

接下来，结合W ink ler关于构造权函数的思想来证明定理1。我们首先通过寻找一个既具有上界又具有下界的函数去证明u（x，t）在空间L2（n+1）（Ω）上是有界的。然后再通过Moser迭代法得到最终结果。

引理5 假设定理1的条件成立，则存在常数C＞0使得对所有的t∈（0，Tmax）有

证明首先令p∶=2（n+1）并且对所有的s≥0有ψ（s）∶=e（1+βs）-κ

我们可以选取充分小的κ＞0使得

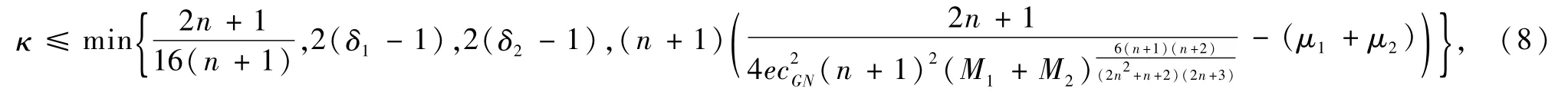
由此可得我们需要的结果。

定理1的证明 利用引理5和Moser-A likakos迭代法可以直接得到u（x，t）在（0，Tmax）上有界，详细过程可参考文献［4，15］。所以结合引理5可得到定理1的证明。

［1］KELLER E F，SEGEL L A.Initiation of slime mold aggregation viewed as an instability［J］.J.Theoret.Biol.1970，26（3）：399-4151.

［2］OSAKIK，YAGIA.Finite dimensional attractors for one-dimensional Keller-Segel equations［J］.Funkcial.Ekvac.2001，44（3）：441-469.

［3］NAGAI T，SENBA T，YOSHIDA K.Application of the Trudinger-Moser inequality to a parabolic system of chemotaxis［J］. Funkcial.Ekvac.1997，40（3）：411-433.

［4］TAO Y，W INKLER M.Boundedness in a quasilinear parabolic-parabolic Keller-Segel system with subcritical sensitivity［J］.J. Differential Equations，2012，252：692-715.

［5］CAO X.Global bounded solutions of the higher-dimensional Keller-Segel system under smallness conditions in optimal spaces［J］.Discrete Contin.Dynam.Syst.Ser.A，2015，35：1891-1904.

［6］W INKLER M.Aggregation vs.global diffusive behavior in the higher-dimensional Keller-Segelmodel［J］.J.Differential Equations，2010，248（12）：2889-2905.

［7］TAO Y，W INKLER M.Eventual smoothness and stabilization of large-data solutions in a three-dimensional chemotaxis systemwith consumption of chemoattractant［J］.J.Differential Equations，2010，252（3）：2520-2543.

［8］LIY.Global bounded solutions and their asymptotic properties under small initial data condition in a two-dimensional chemotaxis system for two species［J］.J.Math.Anal.Appl.，2015，429（2）：1291-1304.

［9］CHOIY S，WANG Z A.Prevention of blow-up by fast diffusion in chemotaxis［J］.J.Math.Anal.Appl.，2010，362（2）：553-564.

［10］DELGADO M，GAYTE I，MORALES-RODRIGO C，SUÁREZ A.An angiogenesismodelwith nonlinear chemotactic response and flux at the tumor boundary［J］.Nonlinear Anal.，2010，72（1）：330-347.

［11］STINNER C，TELLO J I，W INKLER M.Competitive exclusion in a two-species chemotaxis model［J］.J.Math.Biol.，2014，68（7）：1607-1626.

［12］TEMAM R.Navier-stokes equations，theory and numerical analysis［M］.Amsrerdam：North-Holland publishing Co.，1977.

［13］FRIEDMAN A.Partial differential equations［M］.New York：Holt，Rinehart and Winston，1969.

［14］W INKLER M，DJIE K C.Boundedness and finite-time collapse in a chemotaxis system with volume-filling effect［J］.Nonlinear Anal.，2010，72（2）：1044-1064.

［15］ALIKAKOS N D.Lp（Ω）bounds of solution of reaction-diffusion equations［J］.Comn.Partial Differential Equations，1979，4（8）：827-868.

G lobal Boundedness of a Two-species Chemotaxis System

LIDan，MU Chunlai
（College of Mathematical and Statistics，Chongqing University，Chongqing 401331，China）

This paper deals with the global boundedness of the two-species chemotaxis system under homogeneous Neumann boundary condition in a smoothly bounded domainΩ⊂Rn（n≥1），with nonnegative intial data u0，v0∈C0（）and w0∈W1，∞（Ω）.，αi，μ1has a chemotactic sensitivity function and satisfiesχi（w）≤，where the parameters，αi，μ1andμ2are positiveδi＞1.Under the condition thatandμ1+μ2satisfy some specified conditions，the corresponding initial-boundary value problem possesses a unique global classical solution and is uniform ly bounded.

chemotaxis；global boundedness；logistic source

O175.26

A

10.16246/j.issn.1673-5072.2016.01.003

1673-5072（2016）01-0017-08

2016-01-17

国家自然科学基金项目（11371384）；重庆市自然科学基金项目（cstc2015 jcyjBX0007）

李 丹（1991—），女，重庆潼南人，硕士研究生，主要从事偏微分方程的研究。

穆春来（1967—），男，四川雅安人，教授，主要从事偏微分方程的研究。E-mail：clmu2005@163.com