地裂缝场地地铁运行引起框架结构振动的数值分析

许　晨，杨　觅，门玉明，袁立群

（1.长安大学 地质工程与测绘学院，西安 710054；2.聊城大学 建筑工程学院，山东 聊城 252059）

地裂缝场地地铁运行引起框架结构振动的数值分析

许晨1，杨觅1，门玉明1，袁立群2

（1.长安大学 地质工程与测绘学院，西安 710054；2.聊城大学 建筑工程学院，山东 聊城 252059）

针对西安地裂缝场地地铁运行引起地面建筑物的振动问题，建立隧道-地裂缝-地层-框架结构三维有限元模型，进行建筑物的模态分析和振动响应分析，并与同荷载工况的无地裂缝场地框架结构的振动响应进行对比。结果表明：结构的竖向振动比水平向强烈；地裂缝对结构横向和竖向振动加速度的分布影响不大，前者随层高呈波动性分布，后者除首层之外，其余各层差异不大；地裂缝对纵向振动加速度的分布规律影响较大，无地裂缝时呈逐层增加的分布，有地裂缝时呈两端大中间小的分布；地裂缝使结构竖向振动加速度有增大趋势，横向和纵向加速度会在局部楼层增大。

振动与波；地裂缝；地铁；框架结构；数值分析

在西安，地铁1、2号线正在运行，其他线路的建设正在开展。在2号线开通之初，马蒙等、钱春宇等用有限元法及实测法对地铁运行引起钟楼的振动进行了预测和评估［11-12］。西安地铁沿线建筑物众多，由于西安地铁始建较晚，关于地铁振动对建筑物影响的研究相对较少。另外。西安有地裂缝地质灾害，各地铁线路无法避让地穿越了地裂缝，在有地裂缝的特殊场地，地铁运行诱发的振动对建筑物的影响呈现何种规律，是一个值得研究的新领域。本文以西安地铁为工程背景，采用Abaqus软件建立隧道-地裂缝-地层-框架结构三维相互作用的有限元模型，模拟地铁列车车速为80 km/h时体系的振动响应，对地面框架结构的振动进行分析。本研究为深入了解地裂缝场地地铁运行引起的建筑物振动规律及地裂缝对建筑物振动的影响有一定意义，对实际地铁工程的减振设防提供了参考。

1　三维有限元模型

1.1模型建立

综合考虑计算精度及计算代价，截取土体范围为150 m×100 m×50 m，即纵向长150 m，横向宽100 m，竖向高50 m，为进行有地裂缝和无地裂缝条件下地面建筑物振动响应的对比，本文分别建立这两种条件下的有限元模型。其中有地裂缝的模型中地裂缝与地铁隧道正交，缝的倾角为80°，土体被裂缝分为上下两盘，上下盘地表纵向长度分别为90 m、60 m。隧道采用马蹄形截面型式，其截面尺寸如图1所示。

图1　衬砌截面图（单位：m）

隧道顶部埋深15 m。建筑物布置在地裂缝下盘，其边线距隧道中心线10 m，距地裂缝6 m。为控制计算代价，建筑物为单跨框架结构，采用桩筏基础，平面尺寸为6 m×6 m，共8层，层高为3 m。框架梁截面尺寸为250 mm×500 mm，柱截面尺寸为500 mm×500 mm，楼板厚120 mm。基础筏板平面尺寸为0.6 m×0.6 m，厚度为1.2 m。筏板底共布设9根方桩，截面尺寸为500 mm×500 mm，桩长为20 m，横纵向桩距均为3 m。网格划分时，土、衬砌和建筑物均采用八节点线性六面体单元，对邻近衬砌和建筑物的土体进行网格加密，远离结构物的土体网格适当加大。有地裂缝条件模型网格图如图2所示。

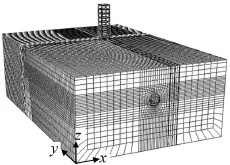
图2　有地裂缝条件模型网格图

1.2材料参数

土层分3层，由底层向上厚度依次为20 m、20 m、10 m。马蹄形衬砌初衬和二衬分别采用C25和C30混凝土。道床为整体式，采用C30混凝土。框架结构、桩筏基础统一采用C30混凝土。各材料物理力学参数如表1所示。

表1　各材料物理力学参数

其中，土层的动力参数由西安地铁南门工点的现场弹性波速测试结果反算得到，静力参数由西安f6地裂缝地段勘查结果中的地层参数通过加权平均而得到；衬砌结构和道床的静动力参数参照文献［13］进行取值，建筑物的静动力参数与二衬相同。所有材料的本构模型均采用理想弹性本构关系。衬砌与土、上下盘土体的接触面法向采用“硬接触”模型，切向采用库仑摩擦模型。衬砌与土、上下盘土与土之间的摩擦系数分别取0.7、0.3。因地铁振动荷载引起的土体和建筑物变形较小，故认为建筑物桩筏基础与土的接触不发生分离，二者协同变形。建模时，建筑物桩筏基础与周围土体的连接采用共用节点的方式。分析时各材料阻尼采用Rayleigh阻尼，其表达式为

早在20世纪五六十年代，谷祺教授就致力于财务成本领域的教学和科研工作。七十年代后期，谷祺教授将以财务计划为核心的部门财务管理学作为自己的研究方向，通过充分借鉴苏联高度集中体制下计划财务管理的理论成果和实践经验，并结合当时中国国民经济建设和企业财务工作的实际情况，形成了一整套原有经济模式下的企业财务管理理论与方法体系。

式中［C］为阻尼矩阵，［M］为质量矩阵，［K］为刚度矩阵，α和β分别为与质量和刚度相关的阻尼系数。根据体系前两阶自振频率和相应的阻尼系数可计算得到各材料的阻尼系数。计算结果见表1。

1.3边界处理

为减小人工截断边界对计算精度造成的影响，较好地模拟地铁运行诱发的振动波由近向远的传播过程，在模型的横向左右侧面及底端采用由Lysmer和Kuhlemeyer［14］提出的人工粘性边界。分析时，在边界引入阻尼系数以达到吸收振动波的目的。在模型的纵向前后侧面采用法向对称边界，模型顶部不加约束。

1.4列车荷载

地铁列车对轨道的竖向荷载可以由静荷载和一系列因不平顺因素而产生的正弦荷载叠加而成，其表达式为

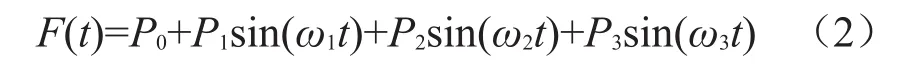
式中p0为车轮静载；p1，p2，p3分别为行车平顺性、作用到线路上的动力附加荷载和轨面波形磨耗三种控制条件下的振动荷载幅值。若列车簧下质量为m0，则相应的振动荷载幅值为

式中ai为对应于各控制条件的典型矢高；ωi为某一车速下对应于各控制条件的不平顺振动波长的圆频率。圆频率的计算式为

式中ν为列车行车速度；Li为对应于各控制条件的典型波长。

结合西安地铁实际，取单边车轮静重P0=70 kN，列车簧下质量m0=750 kg。根据英国轨道不平顺管理值取得三种不平顺条件下的典型振动波长和相应的矢高分别为：L1=10 m，a1=4 mm；L2=2 m，a2=0.5 m；L3=0.5 m，a3=0.08 mm。取ν=80 km/h，计算得到单边车轮动荷载时程曲线如图3所示。

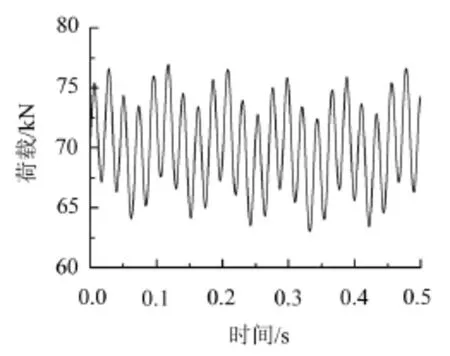
图3　单边车轮动荷载

采用文献［15］中的加载方法，将两相邻车轮的动荷载合并以均布面荷载的形式施加于一个可移动的面板之上，作用面长和宽a=4 m，b=0.6 m。面板与道床平台发生相互作用将动荷载传递于基地，这样便可以实现随时间和位移变化的地铁动荷载。由车轮动荷载F（t）计算得到均布面荷载q（t），从而进行数值计算。分析时，共模拟4节车厢的动荷载，动荷载从地裂缝上盘移动至下盘，初始时刻动荷载前端距地裂缝12.7 m。增量步时长取5.626×10-3s，分析步时长为2.7 s。

2　模拟结果分析

2.1建筑物模态分析

利用Lanczos法提取建筑物的前12阶自振频率，如表2所示。

表2　建筑物前12阶自振频率

前12阶自振频率均小于10 Hz，所以建筑物的振动属于低频振动。建筑物前8阶振型以整体水平运动和扭转为主，第9到12阶振型以竖向运动为主，而且不同的楼层振动有强有弱，竖向运动具有局部性。从理论上来讲，框架结构的竖向刚度一般比水平向刚度大，相应的竖向自振频率要大于水平向自振频率，所以较高频率的外来振动波更容易诱发框架结构较强的竖向振动。文中施加的地铁荷载，不平顺荷载的高中低三个频率约为44 Hz、11 Hz和2 Hz。所以，地铁运行产生的低频段振动波对框架结构水平振动影响较大，中频段振动波对框架结构竖向振动影响较大，高频段振动波对建筑物各方向的振动影响均较小。

2.2地裂缝场地建筑物振动响应的时频域分析

振动加速度是分析建筑物振动响应的重要物理量，本文提取有地裂缝模型建筑物上典型采样点的振动加速度数据进行分析。图4为顶层楼面中心采样点的X向（横向）、Y向（纵向）和Z向（竖向）加速度时程和频谱曲线。

从图4可以看出，建筑物顶层楼面振动Z方向加速度峰值最大，Y方向次之，X方向最小。Z向加速度在2.256 s时刻取得最大值，在2.481 s时刻之后，加速度值已呈现较小趋势，且在2.7 s时刻，模拟的列车车身已越过地面建筑物过半，可以认为曲线在2.7 s内已达到最大值，这说明本次模拟的分析时长是合适的。三个方向上振动加速度主要频率的分布也有显著差异。Z方向加速度幅值谱图只有一个峰值区域，振动优势频率在10 Hz～12 Hz之间；X方向优势振频分布在0～2 Hz和10 Hz～12 Hz，而且1 Hz～3 Hz的振动比10 Hz～12 Hz的振动强；Y方向优势振频主要集中在5Hz以下，而且0～2 Hz的振动比3 Hz～4 Hz的振动强。由此可见，建筑物内的振动主要是低于20 Hz的低频振动，而且Z向的优势振动频率及振动加速度时程峰值要比X向和Y向大。

图4　顶层楼面中心点加速度时程及频谱

2.3建筑物中振动传播及有无地裂缝时的振动响应对比

选择框架结构各层楼面中心为采样点，分别提取有地裂缝和无地裂缝两种条件下隧道-地层-建筑物体系中各采样点的加速度时程峰值，如表3所示。

从表3可以发现，有无地裂缝的条件下，建筑物楼面Z向振动加速度峰值的分布规律是一致的，除底层Z向加速度较小外，上部各层加速度均较大，约为底层加速度的3倍，而且在顶层出现最大值。有地裂缝时的Z向加速度峰值比无地裂缝时略大。所以，框架结构Z向振动加速度随楼层的增加变化并不显著。两种模拟条件下，X向加速度峰值分布规律相近，无地裂缝时X向加速度较大。随楼层增加，X向加速度峰值呈波动性分布。总体上来看，有地裂缝时，加速度峰值随楼层的增加有减小的趋势，而无地裂缝时则有增加的趋势。两种模拟条件下，Y向振动加速度峰值的分布存在显著差异，无地裂缝时，加速度峰值随楼层的增加呈明显的放大趋势；有地裂缝时，加速度峰值呈两端大中间小的分布。从加速度数值来看，有地裂缝时1-3层加速度值较大，其他各层上无地裂缝时的加速度值较大。说明地裂缝的存在对框架结构Y向振动加速度分布影响显著，较无地裂缝时的振动加速度响应而言，有地裂缝时在局部楼层会出现加速度变大的现象。在本次模拟工况之下，对比框架结构3个方向的振动加速度，除部分楼层以外，Z向振动加速度最大，Y向次之，X向最小。

3　结语

通过对地裂缝场地框架结构地铁振动响应的数值计算及与无地裂缝场地框架结构振动响应的对比分析，得到的结论如下：

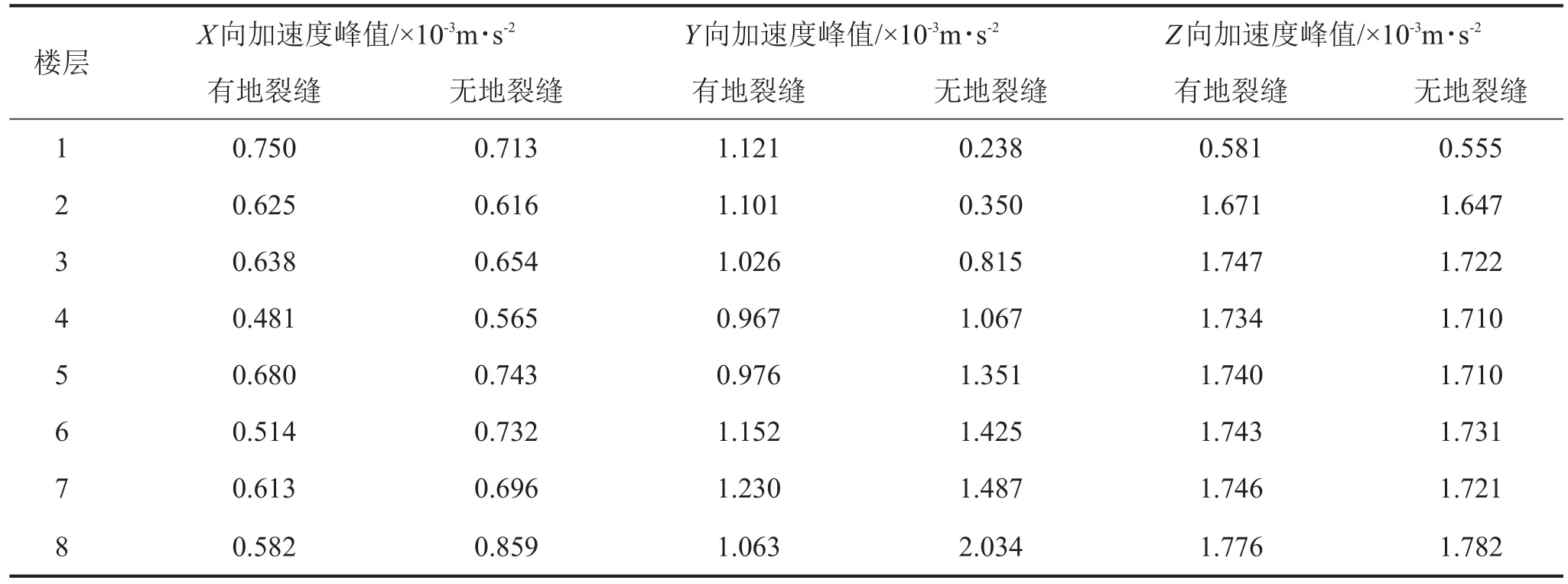
表3　各采样点振动加速度峰值

（1）若按不平顺因素将地铁运行诱发的振动波分为高中低三个频段，则地面框架结构的振动以中低频振动为主，且竖向振动主要是中频振动，水平向振动主要是低频振动。建筑物在某一方向的振动强度与该方向的刚度和不平顺振动波的频率有关，竖向振动属于较高阶模态的振动，且竖向振动加速度一般大于水平向振动加速度。

（2）在本次模拟工况下，无地裂缝时，框架结构横向（X向）和纵向（Y向）振动加速度大体上随层高而增加，且在顶层出现最大值；竖向（Z向）振动加速度在首层较小，在顶层较大，其他各层差异不显著。

（3）在本次模拟工况下，有无地裂缝两种条件时框架结构横向和竖向振动加速度随层高的分布相近，纵向振动加速度随层高的分布差异较大。且有地裂缝时，会使框架结构竖向振动加速度略增，横向和纵向加速度在局部楼层会比无地裂缝时大。另外，需要改变地面框架结构的跨度以及距隧道和地裂缝的距离，进行更多工况的数值分析，以便得到更完善的结论。

［1］刘维宁，马蒙，王文斌.地铁列车振动环境响应预测方法［J］.中国铁道科学，2013，34（4）：110-117.

［2］刘维宁，丁德云，李克飞，等.钢弹簧浮置板轨道低频特性试验研究［J］.土木工程学报，2011，44（8）：118-125.

［3］盛涛，张善莉，单伽锃，等.地铁振动的传递及对建筑物的影响实测与分析［J］.同济大学学报（自然科学版），2015，43（1）：54-59.

［4］夏倩，屈文俊，商晓东.地铁振动对既有砌体结构影响的试验研究［J］.振动与冲击，2013，32（12）：11-16.

［5］洪俊青，刘伟庆.地铁对周边建筑物振动影响分析［J］.振动与冲击，2006，25（4）：142-145.

［6］涂勤明，雷晓燕.地铁引起古建筑物振动三维数值分析［J］.噪声与振动控制，2014，34（5）：130-134.

［7］肖永武，汪浩，唐和生，等.地铁引起建筑结构振动及室内辐射噪声的数值分析［J］.结构工程师，2014，30（6）：77-84.

［8］NIE H，YAN W M，ZHOU X Y.The numerical simulation analysis of adjacent building vibration induced by urban subway transit［C］.Second International Conference on Mechanic Automation and Control Engineering.IEEE，2011:7010-7014.

［9］PATRÍCIA L，JÉSUS FERNÁNDEZ R，PEDRO A C，et al. Vibrations inside buildings due to subway railway traffic. Experimental validation of a comprehensive prediction model［J］.Science of the Total Environment，2015.

［10］楼梦麟，李守继.地铁引起建筑物振动评价研究［J］.振动与冲击，2007，26（8）：68-71.

［11］马蒙，刘维宁，邓国华，等.基于校准法的地铁振动对西安钟楼影响研究［J］.工程力学，2013，30（12）：206-212.

［12］钱春宇，郑建国，宋春雨.西安钟楼台基受地铁运行振动响应的分析［J］.世界地震工程，2010，26（增刊）：177-181.

［13］黄强兵.地裂缝对地铁隧道的影响机制及病害控制研究［D］.西安：长安大学，2009.

［14］LYSMER J，KUHLEMEYER R L.Finite dynamic model forinfinitemedia［J］.JournaloftheEngineering Mechanics Division，ASCE，1969，95（4）:859-877.

［15］杨觅，门玉明，贾朋娟.地铁动荷载作用下隧道-地裂缝-地层的三维动力响应［J］.灾害学，2015，30（3）：61-66.

NumericalAnalysis for Frame Structure Vibration Induced by Metro Operation in Ground FissureArea

XUChen1，YANGMi1，MEN Yu-ming1，YUAN Li-qun2
（1.School of Geology Engineering and Geomatics，Chang′an University，Xi′an 710054，China；2.School ofArchitecture and Civil Engineering，Liaocheng University，Liaocheng 252059，Shandong China）

Focusing on the vibration problem of buildings induced by Xi’an metro operation in ground fissure area，a three-dimensional finite element model including tunnel，ground-fissure and frame-structure is established.Model analysis and vibration response analysis of the buildings are conducted.The results are compared with those of the same model under the same loading condition but the ground fissure effect is not considered.It is indicated that the structure’s vertical vibration is stronger than the horizontal one；the ground fissure has little effect on the distributions of horizontal and veridical vibration accelerations.The former shows a fluctuating distribution with the floor rising，while the latter only shows insignificant difference of all the floors except the first floor.The ground fissure has large influence on the distribution of the vertical acceleration.It increases with the floor rising in the non-ground fissure area，while in ground fissure area，it decreases initially and increases later with the floor rising.The ground fissure causes the increasing of frame’s vertical vibration acceleration，both vertical and horizontal vibration acceleration increases in some floors.

vibration and wave；ground fissure；metro；frame structure；numerical analysis

U211.3

DOI编码：10.3969/j.issn.1006-1335.2016.05.025

1006-1355（2016）05-0117-05

2016-06-29

国家自然科学基金项目（41172257）；国家自然科学基金青年项目（41502277）；中央高校基金310826162005

许晨（1982-），女，湖北省武汉市人，博士研究生，讲师，主要从事建筑安全管理方面研究。E-mail:xuchen@chd.edu.cn