共振速度下轨道交通槽形梁结构瞬态噪声分析

刘林芽，曾　峰，姚忠達，许代言

（1.华东交通大学 铁路环境振动与噪声教育部工程研究中心，南昌 330013；2.台湾淡江大学 土木工程学系，台湾 新北 25137）

共振速度下轨道交通槽形梁结构瞬态噪声分析

刘林芽1，曾峰1，姚忠達2，许代言1

（1.华东交通大学 铁路环境振动与噪声教育部工程研究中心，南昌 330013；2.台湾淡江大学 土木工程学系，台湾 新北 25137）

为了进一步研究不同列车速度下的桥梁结构噪声问题，基于有限元-瞬态边界元理论，针对轨道交通30 m简支槽形梁，分析在共振、消振速度下桥梁的振动响应及结构声辐射特性。首先，建立槽形梁振动辐射瞬态噪声的有限元/边界元模型；然后，对简支梁在移动列车荷载下诱发的振动进行分析，得到列车荷载通过桥梁时的共振和消振速度；最终，结合声辐射理论，采用瞬态边界元法研究分析不同列车速度引起的桥梁瞬态噪声声场特性。研究结果表明:列车速度的变化引起桥梁结构的位移幅值出现波动性变化；桥梁结构的振动加速度幅值随着速度的增大而不断增大；桥梁结构辐射噪声的变化趋势与结构的振动加速度变化趋势有一定的相关性；当列车以共振速度通过简支桥梁时，结构动力响应值及辐射噪声值有放大趋势，在附近出现峰值；列车共振速度对桥梁结构的远声场瞬态噪声影响效果较为显著；应有针对性地控制列车速度以改善桥梁结构噪声。

振动与波；槽形梁；移动荷载；共振；消振；瞬态声辐射特性

随着经济的飞速发展，城市化进程的加快，城市交通拥堵问题日益严峻，而世界各国普遍认识到，缓解城市拥堵的根本出路在于发展以城市轨道交通为主的公共交通系统。高架桥梁因其造价低、美观等优势，在城市轨道交通全线中所占的比重也越来越大。伴随着高架桥承受的交通流量日益增多，列车荷载作用下桥梁的振动与噪声问题也逐渐受到人们的关注。其中列车过桥时引起的共振问题一直是国内外相关学者关注的重点，人们对这个问题进行了较为系统的研究，取得了很多成果。

Yang等采用解析法研究了移动荷载作用下两端弹性支承简支梁的共振、消振现象［1-2］。Yau等采用解析法、数值法相结合研究了移动荷载作用下多跨连续梁的振动响应［3］。Xia等分别从理论分析、数值模拟及试验分析出发，研究了列车荷载作用下简支梁的振动响应理论解，获得简支梁发生共振及消振的车速计算公式［4，6］。黄方林等通过建立时变的移动荷载-简支梁系统，研究了桥梁结构的竖向振动［7］。以上研究，对共振速度引起的结构辐射噪声问题较少涉及。

吴定俊等研究指出桥梁结构辐射噪声与列车车速有一定的关系，但目前还无权威定论［8］。Moritoh等通过对高速铁路高架线的测试研究发现：距离高架桥线路中心25 m时桥梁结构噪声与列车速度有一定的相关性［9］。Au等对移动荷载作用下的正交各向异性薄板的振动声辐射问题进行分析，分析表明，移动荷载的速度越大，产生的声压越大［10］，而刘加华研究指出结构的低频噪声随列车速度的增大无显著变化［11］，贺建良等研究发现，车速越低，桥面振动辐射噪声对总噪声的贡献越大［12］。因此，列车速度对桥梁结构噪声的影响，尤其列车共振速度下诱发的高架桥梁结构低频噪声问题还须进一步研究。

本文以某拟建轨道交通槽形梁为研究对象，针对简支梁在移动列车荷载下诱发的振动进行分析，得到列车荷载通过桥梁时的共振和消振速度，基于有限元-瞬态边界元理论，建立轨道-槽形梁有限元模型和声学边界元模型，采用移动荷载模型，并以该模型激励下得到的槽形梁结构振动响应作为声源，采用瞬态边界元法分析桥梁振动产生的声场，计算不同列车速度下槽形梁结构瞬态声辐射情况，为控制共振速度下的车桥振动诱发的结构噪声控制提供了可行性方案。

1　分析模型

1.1移动列车荷载模型

为了更好地反映列车通过桥梁时，因荷载周期性加载引起的桥梁振动互相叠加出现的共振现象，及其对桥梁结构辐射噪声的影响，本文采用移动列车荷载模型，高传伟等研究表明采用移动列车荷载模型分析城市轨道交通桥梁的动力响应，分析精度是足够的［13］。

移动列车荷载模型可以分析车长、轴距、轴重和车速等参数对桥梁辐射噪声的影响及规律。结合国内（上海、广州、南京、重庆等）已使用的列车车辆资料，城市轨道交通车辆竖向荷载可以简化为如图1所示的荷载列。

图1　移动列车轴重荷载过桥分析模型

移动列车荷载将每节列车的轴重荷载用集中力P表示，并参照轮对实际位置布置，荷载之间存在以下几种间距排列：Lv为车辆全长；Lc为转向架中心距；Lw为轮对的轴距。

1.2轨道交通槽形梁有限元模型

基于有限元理论，建立轨道交通槽形梁模型，在分析模型中，所有材料均处于线弹性阶段，将钢轨视为Euler梁，用梁单元模拟；槽形梁梁体、轨道板、CA砂浆层均用实体单元模拟，为避免病态网格的出现，采用体扫掠法划分将其划分为大小合适的六面体单元；连接钢轨与轨道板的扣件系统采用间距为0.625 m的离散弹簧阻尼单元模拟，主要材料参数如表1。

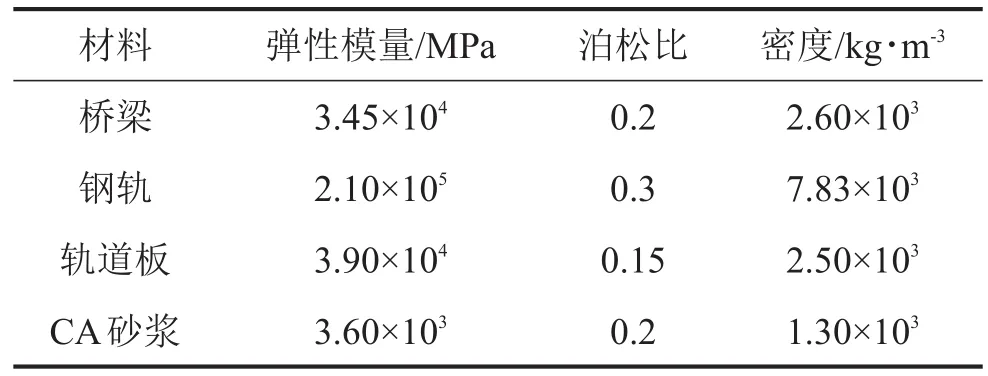
表1　槽形梁模型主要材料参数表

槽形梁的截面形式采用某拟建轨道交通选用的简支槽形梁，梁体腹板一侧为圆弧结构、另一侧采用折腹线式直线的不对称结构，有限元模型如图2所示。各项参数经过多次调试，能满足GB50157-2013地铁设计规范的要求。

图2　轨道交通槽形梁有限元模型

1.3轨道交通槽形梁边界元模型

瞬态边界元法就是基于有限元法求解的桥梁瞬态动力响应结构通过插值的方法分配到桥梁结构声学边界元网格上作为边界条件，然后求解出槽形梁的瞬态声辐射特性。

槽形梁的表面为封闭的边界表面，通过对其离散，可以得到边界元求解方程

其中A、B为系数矩阵；p（ra）、vn（ra）分别是封闭边界表面Ωa的声压和方向速度。槽形梁表面外部无限域V内任意一点的声压可以通过Helmholtz积分方程求得。

瞬态边界元法用于计算桥梁结构振动声辐射问题时，不仅能够反映声压在时间域的分布，并且能够合理反映列车荷载作用下桥梁辐射低频噪声情况，同时避免了采用模态叠加法时出现的模态截断误差，与稳态边界元相比，避免了对边界条件进行稳态简化，计算精度更有保障。

本文基于瞬态边界元理论建立槽形梁结构声辐射边界元模型，如图3所示。

图3　轨道交通槽形梁边界元模型

在进行瞬态边界元分析计算时，边界元网格必须是三角形网格，故使用自由网格划分。

2　移动列车荷载下的共振分析

北京交通大学夏禾教授等对简支梁桥的车桥竖向共振问题进行了研究，他采用移动的荷载列来模拟车辆模型，通过振动响应分析得出任意模态下桥梁的共振及两类消振的解析表达式［14］

式中Vres为共振列车速度，Vcan为消振列车速度。f1为桥梁1阶竖向自振频率，本文中f1=3.165 7；Lv=20 m，为车辆全长；L为桥梁全长，本文L=30 m；α为无量纲参数，α=1表示第一类消振效应。

根据图1可以计算出不同桥梁跨径的1阶竖向振动，然后代入式（2）、式（3）可以计算出车辆和桥梁的竖向共振速度和消振速度，计算结果见表2，并将大于120 km/h，小于40 km/h的速度舍弃。

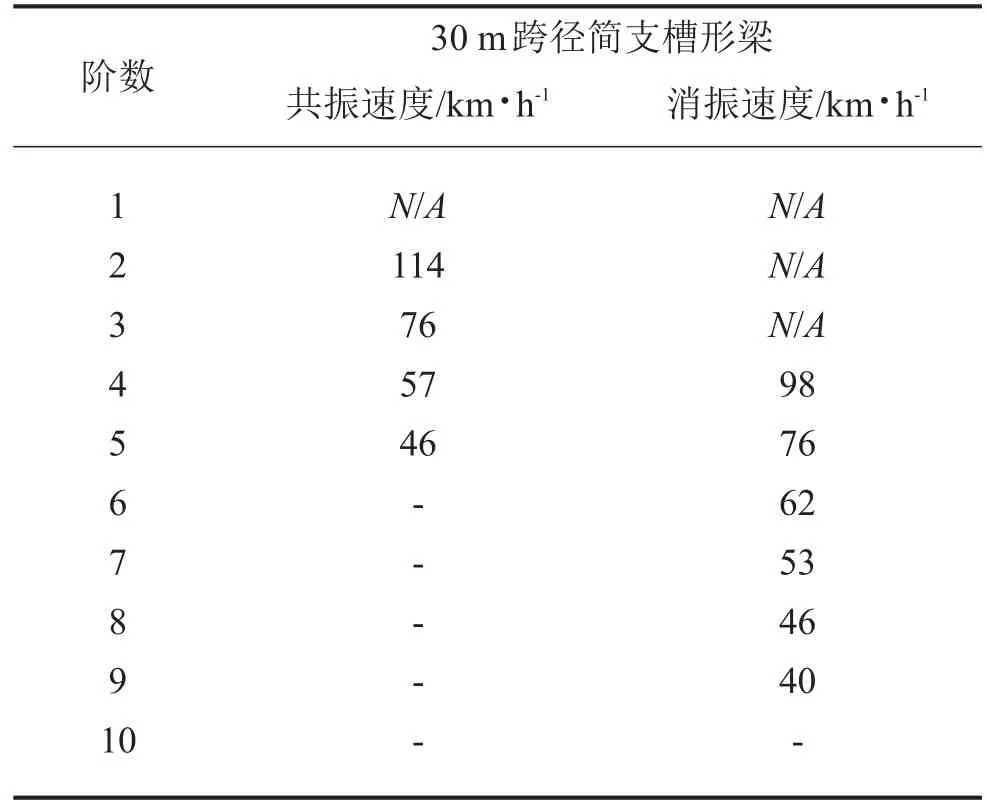
表2　简支槽形梁1阶振型的共振与消振车速

3　计算结果与分析

3.1轨道交通槽形梁的动力响应计算与分析

重点研究共振速度下桥梁结构的振动响应，不考虑桥上车辆的振动情况，因此车辆与桥梁的耦合作用不再考虑。车辆模型简化为匀速运动的集中荷载列。

结构振动辐射噪声主要由桥梁的法向振动响应产生，由于移动荷载的周期性排列，会对桥梁结构产生周期性作用，这对桥梁结构的振动响应具有重要影响。计算中保持其它参数不变，对列车速度在40 km/h～120 km/h范围内的轨道交通槽形梁结构动力响应进行分析。选取桥梁跨中截面底板输出不同车速下桥梁结构的振动响应计算结果，如图4、图5所示。

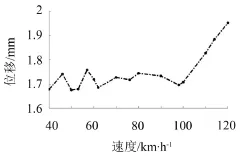
图4　轨道交通槽形梁底板跨中最大位移

图4和图5分别给出了不同列车时速下桥梁跨中截面底板的最大位移值和最大加速度值的变化情况。从图4中可以看出：随着速度的增加，桥梁跨中竖向最大位移值出现波动性变化。从图5中可以看出：随着速度的增加，桥梁各跨的竖向振动加速度随着车速的增加几乎呈线性增加。在共振速度处，加速度值有放大趋势，在附近出现峰值。从相关系数R=0.978 7可以看出，列车速度跟桥梁结构振动加速度值两者之间的相关性较为显著。

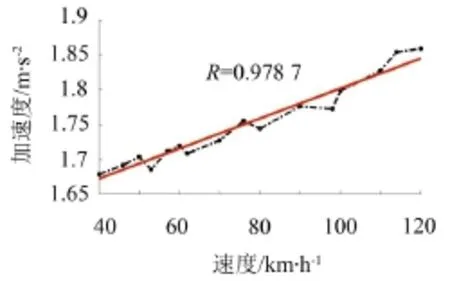
图5　轨道交通槽形梁底板跨中最大加速度

表3给出了共振与消振速度下桥梁跨中底板最大加速度值对比分析。据图5可知，列车速度跟桥梁结构振动加速度值两者之间的相关性较为显著，现根据列车速度在40，50，60，...，120 km/h时对应的桥梁跨中底板最大加速度值，进行线性拟合，获取共振/消振速度下桥梁跨中截面底板最大加速度拟合值，并与数值仿真结果进行差值对比分析。由表3可知，在共振速度114 km/h处，加速度差值有放大趋势，而在46 km/h，76 km/h处加速度差值很小，这是源于消振速度对其的影响，抑制了结构的共振现象。

表3　共振/消振车速下桥梁最大加速度值对比分析

3.2轨道交通槽形梁瞬态声辐射特性分析及场点分布

为了很好地体现桥梁结构振动随时间变化的声场特性，采用瞬态边界元法对轨道交通槽形梁进行结构瞬态声辐射特性分析，将移动列荷载作为外部激振力加载到轨道-槽形梁有限元模型上，计算得到桥梁瞬态动力响应，作为槽形梁声学边界元模型的初始边界条件，对槽形梁的瞬态辐射噪声进行分析计算。

在时域内计算槽形梁结构声学响应时，由于只研究槽形梁梁体结构噪声，因此忽略了桥墩的影响，拟建桥梁辐射声场场点如图6所示。

图6　场点分布图

3.3轨道交通槽形梁瞬态声辐射计算与分析

采用有限元软件，建立轨道-槽形梁有限元模型，并将采用基于移动列车荷载模型加载激振力到所建立的有限元模型上，进行槽形梁的瞬态动力响应分析，以槽形梁动力响应结果作为边界条件，预测分析不同列车速度下槽形梁梁体瞬态噪声情况。同时，为了更好地反映共振速度下轨道交通槽形梁结构噪声的空间辐射情况，分别选取1号场点作为近声场评价点，3号场点作为远声场的评价点。

图7、图8分别给出了不同列车时速下轨道交通槽形梁辐射声场1号场点和3号场点的最大声压级。据图可知：随着列车速度的增加，桥梁结构辐射噪声最大声压级越大，列车速度越高，对高架桥梁结构噪声的影响越明显。在共振速度处，最大声压级值有放大趋势，在附近出现峰值。从相关系数R可以看出，列车速度跟桥梁结构振动辐射声压级值两者相关性较为显著。

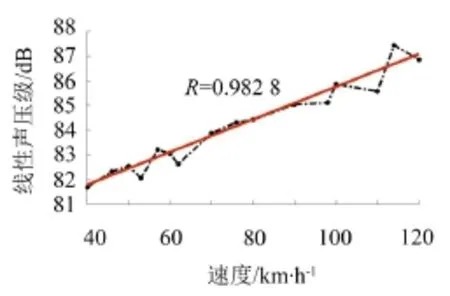
图7　轨道交通槽形梁辐射声场1号场点最大声压级

图8　轨道交通槽形梁辐射声场3号场点最大声压级

表4给出了共振与消振速度下轨道交通槽形梁辐射声场1号场点和3号场点的最大声压级值对比分析。分析图7、图8可知，列车速度跟槽形梁辐射声压级两者之间的相关性较为显著，现依据列车速度在40，50，60，...，120 km/h时对应的桥梁辐射声场最大声压级值，进行线性拟合，获取共振/消振速度下桥梁1号场点和3号场点的最大声压级值拟合值，并于数值仿真结果进行差值对比分析。

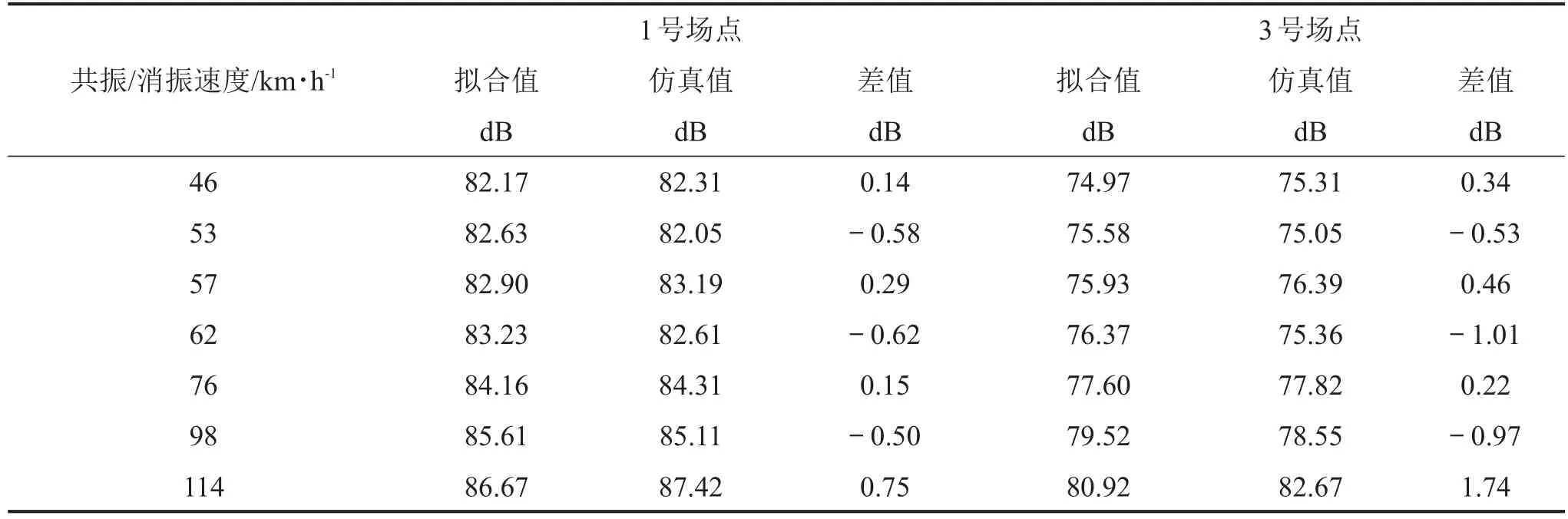
表4　共振/消振车速下场点最大声压级值对比分析

由表4可知，在共振速度114 km/h处，最大声压级值有放大，而在46 km/h，76 km/h处最大声压级差值相对较小，这是源于消振速度对其的影响，抑制了结构的共振现象。同时，对比发现，在共振速度57 km/h、114 km/h等处，3号场点的结构瞬态噪声最大声压级差值与1号场点相比相对较大，可见列车共振速度对桥梁结构的远声场瞬态噪声影响效果较为显著。

4　结语

本文以某拟建轨道交通高架简支槽形梁为研究对象，针对简支梁在移动列车荷载下诱发的振动进行分析，得到列车荷载通过桥梁时的共振和消振速度，结合声辐射理论，采用瞬态边界元法研究分析不同列车速度引起的桥梁瞬态噪声声场特性，通过数值分析得到以下结论：

（1）随着列车速度的变化，桥梁结构的位移幅值出现波动性变化，桥梁结构的振动加速度幅值随着速度的增大而不断增大。

（2）桥梁结构辐射噪声的变化趋势与结构的振动加速度变化趋势有一定的相关性。

（3）当列车以共振速度通过简支桥梁时，结构振动以及辐射噪声有放大趋势，在附近出现峰值，这为控制列车运行速度避开桥梁共振提供了理论参考。

（4）列车共振速度对桥梁结构的远声场瞬态噪声影响效果较为显著。

［1］YANG Y B，YAU J D，HSU L C.Vibration of simple beams due to trains moving at high speed［J］.Engineering Structures，1997，19（11）:936-944.

［2］YANG Y B，LIN C L，YAU J D，et al.Mechanism of resonance and cancellation for train-induced vibrations on bridges with elastic bearings［J］.Journal of Sound and Vibration，2004，269（1/2）:345-360.

［3］YAU J D.Resonance of continuous bridges due to high speed trains［J］.Journal of Marine Science and Technology Taiwan，2001，9（1）:14-20.

［4］夏禾，郭薇薇，张楠.车桥系统共振机理和共振条件分析［J］.铁道学报，2006，28（5）：52-58.

［5］XIA HE，LI H L，GUO W W，et al.Vibration resonance andcancellationofsimplesupportedbridgesunder movingtrainloads［J］.JournalofEngineering Mechanics ASCE，2014，140（5）:04014015.1-04014015. 11.

［6］李慧乐，夏禾，郭薇薇.移动列车荷载作用下简支梁共振与消振机理研究［J］.工程力学，2013，30（7）：47-54.

［7］陶胜利，黄方林，黄志辉.移动荷载速度对梁桥跨中动力响应影响的分析［J］.噪声与振动控制，2009，29（2）：27-29.

［8］韩江龙，吴定俊，李奇.城市轨道交通高架结构噪声研究的进展［J］.城市轨道交通研究，2012，15（3）：109-112+116.

［9］MORITOH Y，ZENDA Y，NAGAKURA K.Noise control of high speed shinkansen［J］.Journal of Sound and Vibration，1996，193（1）:319.

［10］AU F T K，WANG M F.Sound radiation from forced vibration of rectangular orthotropic plates under moving loads［J］.Journal of Sound and Vibration，2005，281（3-5）:1057.

［11］刘加华.从轨道结构降低城市轨道交通高架结构振动与噪声的研究与应用［D］.上海：同济大学，2006.

［12］贺建良，万泉，蒋伟康.高架城市轨道交通的噪声特性分析［J］.城市轨道交通研究，2007，10（8）：57.

［13］高传伟，唐雅茹，余华.基于移动荷载过桥的轨道交通桥梁振动研究［J］.中国铁道科学，2005，26（2）：73-76.

［14］李慧乐，夏禾，郭薇薇.简支梁在列车荷载下的共振与消振效应［J］.振动工程学报，2014，27（2）：172-179.

Transient NoiseAnalysis of Rail Transit Trough-shaped Beam Structures under Resonant Speeds

LIU Lin-ya1，ZENGFeng1，YAU Zhong-da2，XU Dai-yan1
（1.Engineering Research Center of Railway Environmental Vibration and Noise，Ministry of Education，East China Jiaotong University，Nanchang 330013，China；2.Department of Civil Engineering，Tamkang University，New Taipei 25137）

In order to further study the structural noise of bridges under different train speed condition，the structural noise and sound radiation characteristics of a rail-transit trough-shaped 30 m-span simply-supported beam are analyzed by means of finite element method and transient boundary element theory.First of all，the finite element and boundary element model of the trough-shaped beam is established.Then，vibration of the simply supported beam under moving load excitation is analyzed，and the resonance speed and the vibration suppression speed are obtained.Finally，using the theory of sound radiation combined with the transient boundary element method，the characteristics of the transient noise of the beam induced by different train speeds are calculated and analyzed.The results show that the train-speed change can cause fluctuation of the displacement amplitude of the beam structure.The vibration acceleration of the beam structure increases with the increasing of the train speed.Variation of the radiation noise of the beam structure is somewhat correlated with that of the structure vibration acceleration.When the train is traveling through the beam bridge at the resonance speed，the dynamic response and the radiation noise of the structure will be obviously amplified.The transient noise of the beam bridge structure is also significant under resonant speed in the far acoustic field.So，the train speed should be controlled in order to reduce the noise of the beam bridge structure.

vibration and wave；trough-shaped beam；moving load；resonance；vibration suppression；transient sound radiation characteristic

U239.5；U491.91

ADOI编码：10.3969/j.issn.1006-1335.2016.05.024

1006-1355（2016）05-0112-04

2016-03-06

国家自然科学基金资助项目（51268014）、（51578238）；江西省“赣鄱英才555工程”领军人才培养计划项目

刘林芽（1973-），男，江西省樟树市人，教授，博士，博士生导师，主要研究方向为铁路环境振动与噪声。E-mail:316058254@qq.com