考虑管状药束轴向运动的大口径平衡炮二维内弹道模型的建立与仿真

蒋淑园， 王浩， 林长津， 王金龙

(南京理工大学 能源与动力工程学院， 江苏 南京 210094)



考虑管状药束轴向运动的大口径平衡炮二维内弹道模型的建立与仿真

蒋淑园， 王浩， 林长津， 王金龙

(南京理工大学 能源与动力工程学院， 江苏 南京 210094)

传统的两相流内弹道模型将火药颗粒作拟流体假设，对于采用长管状药装药的大口径高速平衡炮来说误差较大。为解决这一问题，针对管状药模块化装填的某480 mm口径高速平衡炮提出在欧拉坐标系中考察火药气体的流动情况，在拉格朗日坐标系中追踪管状药束的运动规律；同时针对药束径向运动方程难以建立的问题，提出药束沿径向线性排布药束的思想，建立了考察管状药束沿轴向的运动规律并能够描述火药气体沿轴向和径向的流动情况的内弹道模型，编制程序进行了数值模拟。通过计算结果与试验结果的对比分析，证明了建立的模型有效，得到了火药气体在轴向和径向的压力分布以及药束模块的运动轨迹，为平衡炮内弹道性能的深入研究提供了新的思路。

兵器科学与技术； 平衡炮； 内弹道； 两相流； 数值模拟

0　引言

平衡炮可以使炮膛轴线方向上，作用力基本平衡，达到较高的预期速度，同时炮架承载很小, 因而炮口径可以做到很大,是研究大尺寸、大质量试验件的有效试验加载工具，解决了缩比试验所带来的局限性，对于侵彻动力学研究、材料动态响应、引战配合技术等很多领域的研究具有十分重要的意义[1-5]。随着武器系统研究的不断深入[6]，平衡炮发射技术也不断完善，正朝着大口径、高炮口动能、大装药量和高稳定性的方向不断发展。这也意味着，膛内高温高压、高速与瞬变的两相流动与燃烧的过程更为复杂，给内弹道学的研究带来很多的困难。

近年来，两相流内弹道理论[7-8]已经实现了对经典内弹道理论的巨大突破。但是，大部分内弹道方面的两相流研究都是基于拟流体的假设。大口径高速平衡炮中为增加药床透气性常采用管状火药，拟流体假设对于尺寸较大的管状火药必然存在较大的误差。文献[9]中试图将管状药作非流体相处理，将管状药床看成一个在两端面压力差和相间阻力共同作用下可沿轴向运动的整体,相间质量能量输运通过控制方程中的源项实现，应用新模型与重叠网格技术对平衡炮内弹道过程建立了内弹道一维两相流模型进行仿真计算，但固相作为一个整体的处理方式对研究固相的运动过程依然存在局限性。本文基于欧拉- 拉格朗日方法[10]，即在欧拉坐标系中考察气相在轴向和径向的运动，而在拉格朗日坐标系中考察管状药模块在轴向的运动规律，建立某平衡炮的二维内弹道模型并进行模拟，为掌握大尺寸装药的火炮内弹道性能提供新的思路。

1　平衡炮系统结构

平衡炮是利用平衡体在炮管内反向运动,使炮膛轴线方向上作用力基本平衡，有效抵消火炮发射时的后坐力，实现大质量弹丸的高速发射。结构示意图如图1所示。装药点传火设计为多点点火和中心传火管传火。发射主装药则采用双芳48/1管状药，装药结构示意图如图2所示。发射药被均匀分成9等份，用白拉带均匀捆绑于9个点火具，两个固定架之间，组成装药模块，从平衡体底部到弹丸底部依次排列，依次编号1～9. 图3分别为装药结构实物图。

图1　平衡炮系统结构示意图Fig.1　Structure diagram of Davis gun system

图2　火炮装药结构示意图Fig.2　Schematic diagram of charge arrangement

图3　某平衡炮装药照片Fig.3　Photo of charge of a Davis gun

2　数值模型及数值计算方法

2.1基本假设

研究涉及的平衡炮装药量大，膛内压力高，火药燃烧剧烈，同时又涉及两个发射体的运动，实际的膛内过程非常复杂，因此对平衡炮膛内发射过程的数值模拟提出以下8个重要假设：

1)假定气相为沿轴向和径向的二维流动，管束以模块为单元沿轴向运动，混合物为无黏。用欧拉法描述气体非定常流动，用变质量的质量、动量守恒方程描述管状药束运动。

2)忽略管状药的湍流黏性和扩散效应。

3)管状药以装药模块为单位，分为9个单元，各单元内每根药条的形状、尺寸与性质完全相同，燃烧规律和运动规律也相同。

4)管状药模块与弹丸或平衡体底部壁面发生碰撞时，由于弹丸和平衡体质量远远大于火药模块质量，因此假设碰撞后，火药模块速度等于相应壁面的速度。

5)管状药作用于气相场的质量源、动量源和能量源反映在气相方程的源项中。

6)管状药条着火准则采用表面温度准则，假设管状药条表面燃烧速度相同，忽略药条表面的温度差。同时，以药条表面压力的平均值计算燃速。

7)假设管状药内外同时点燃，且燃烧规律相同，由于48/1 管状药长径比超过20,可以忽略管状药的端面燃烧。

8)药束初始时，固定在炮膛中心轴处，发射开始后，管状药束在径向也必然存在运动，向身管外壁扩散，但是由于理论研究的困难性，现有的研究中仍然没有学者对管状药束沿径向的运动建立有效的模型。若按初始状态集中固定不散开，或者作散开后均匀化处理又无法有效地描述径向的流场运动。因此，本文提出如下假设：自中心轴往身管壁面，药条在沿轴向每个截面的径向占有量由密到疏线性排布，即在中心轴处药条较多，空隙率约为0.2左右，靠近身管外壁处假设空隙率为1.0，从中心轴到外壁空隙率按线性规律依次递增。该假设简化了径向运动规律，使得研究可行，另一方面，药束沿中心轴往壁面散开与实际情况也有相似之处，可以在一定程度上反映径向效应。图4为与该假设所对应的从药室横截面上看的药条排布示意图。

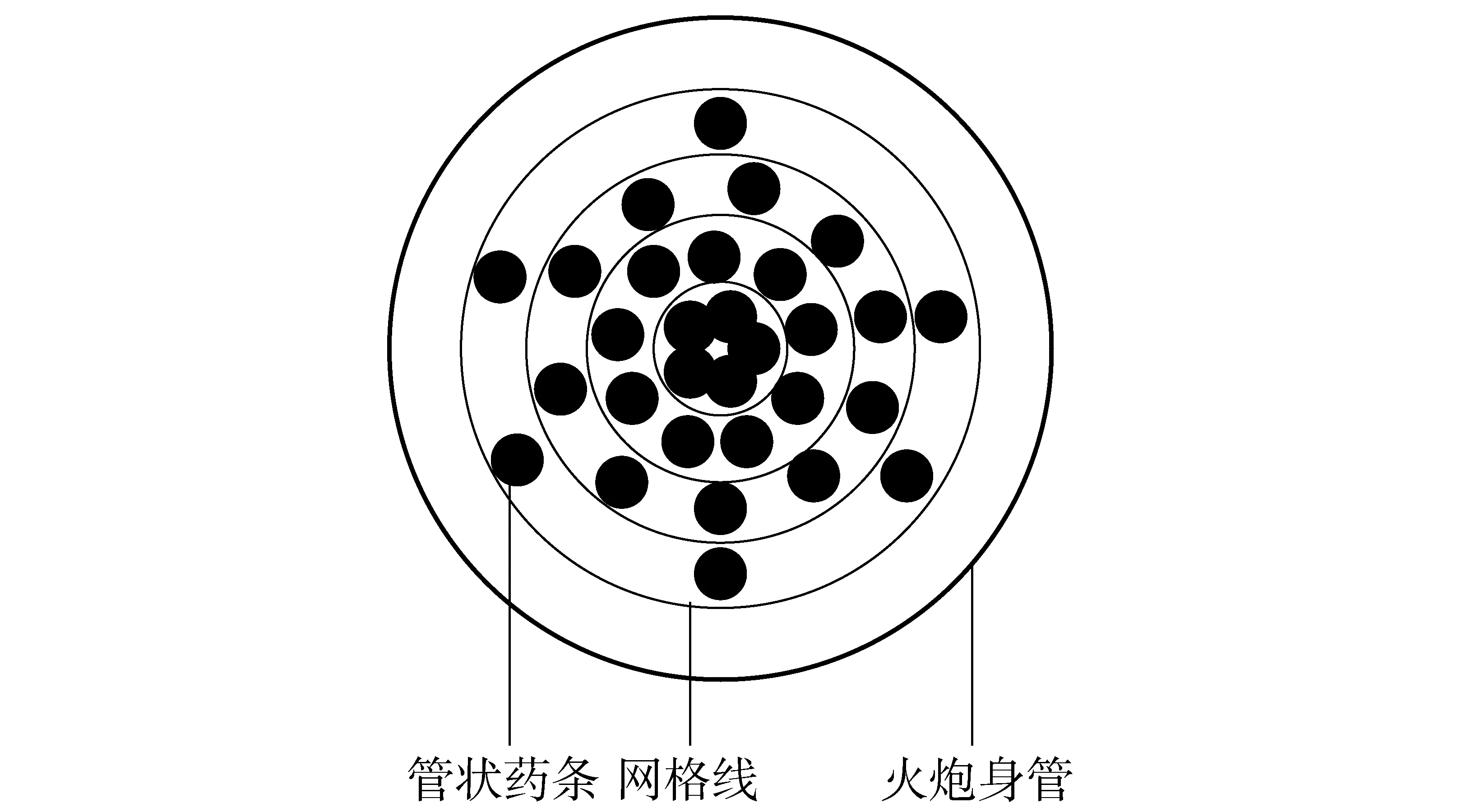
图4　药条排布示意图Fig.4　　　　Structure diagram of arrangement of tubular charge clusters

2.2数学模型

基于以上假设，对膛内火药气体和管状药束分别建立数学模型如下：

2.2.1气相守恒方程

1)气相连续方程

(1)

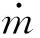
2)气相动量方程。

径向:

(2)

式中：p为气体压力；upr为火药生成燃气的径向运动速度，即药条径向速度；uign,r为从点火管内流入主装药的气体速度径向分量；fsr为相间阻力的径向分量。

轴向：

(3)

式中：upz为火药生成燃气的轴向运动速度，即药条轴向速度，upr=0；uign,z为从点火管内流入主装药的气体速度轴向分量；fsz为相间阻力的轴向分量。

3)气相能量方程

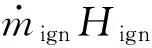
(4)

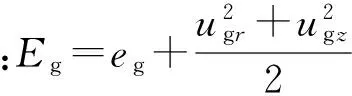
2.2.2管状药运动方程

(5)

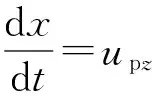
(6)

式中：x为药束轴向位移；A为网格截面积。

2.2.3弹丸和平衡体运动方程

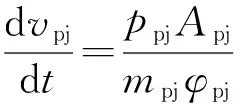
(7)

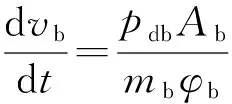
(8)

式中：vpj、mpj、Apj、ppj分别为弹丸速度、质量、截面积、底部压力；vb、mb、Ab、pb分别为平衡体速度、质量、截面积、底部压力；φpj、φb为次要功系数。

2.2.4辅助方程

1)相间阻力。管状药床的摩擦阻力系数[11]为

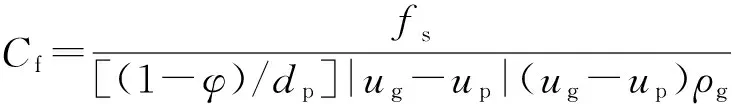
式中：fs为相间阻力；dp为火药颗粒当量直径。

2)其他辅助方程。包括火药燃烧速度方程、相间热交换、状态方程、形状函数和火药表面温度方程，参见文献[12]。

3　数值模拟与结果分析

对上述数值方程组中的气相方程采用预估校正二步MacCormack 差分格式[13]求解，初始条件为装填条件，求解过程中时间步长符合CFL稳定性条件，弹丸和平衡体启动前采用固壁边界，启动后采用运动控制体法推导出各自运动边界条件。模块之间的碰撞按完全弹性碰撞进行处理。编制程序计算从点火开始直至弹丸出炮口这一过程的膛内情况。计算以某480 mm口径平衡炮射击试验为背景，平衡体运动到炮口距离为5.1 m，药室长4.6 m，弹丸到炮口距离21.1 m. 试验共进行了两发，第1发试验弹丸质量1 310 kg，平衡体质量7 000 kg，装药质量约369 kg；第2发试验弹丸质量1 500 kg，平衡体质量7 000 kg，装药质量约387 kg.

图5～图10为两发试验分别在3个位置处的压力测试曲线和计算曲线对比图。其中1号测压点置于药室处，距离平衡体端炮口约5.2 m处，2号和3号测压点则在药室和弹丸出口之间的身管上，距弹丸端炮口分别为14.5 m和5.3 m. 从图5和图6的药室处的压力曲线对比来看，曲线整体上吻合较好。从图7～图10 中其他位置的压力曲线来看，计算结果与试验结果都较为吻合，说明计算的误差控制在合理的范围内，采用的方法以及建立的模型对于内弹道性能的研究有参考价值。

图5　第1发1号位置处压力曲线Fig.5　　　　Curves of calculated and experimental pressures at No.1 position (Test 1)

图6　第2发1号位置处压力曲线Fig.6　　　　Curves of calculated and experimental pressures at No.1 position (Test 2)

图7　第1发2号位置处压力曲线Fig.7　　　　Curves of calculated and experimental pressures at No.2 position (Test 1)

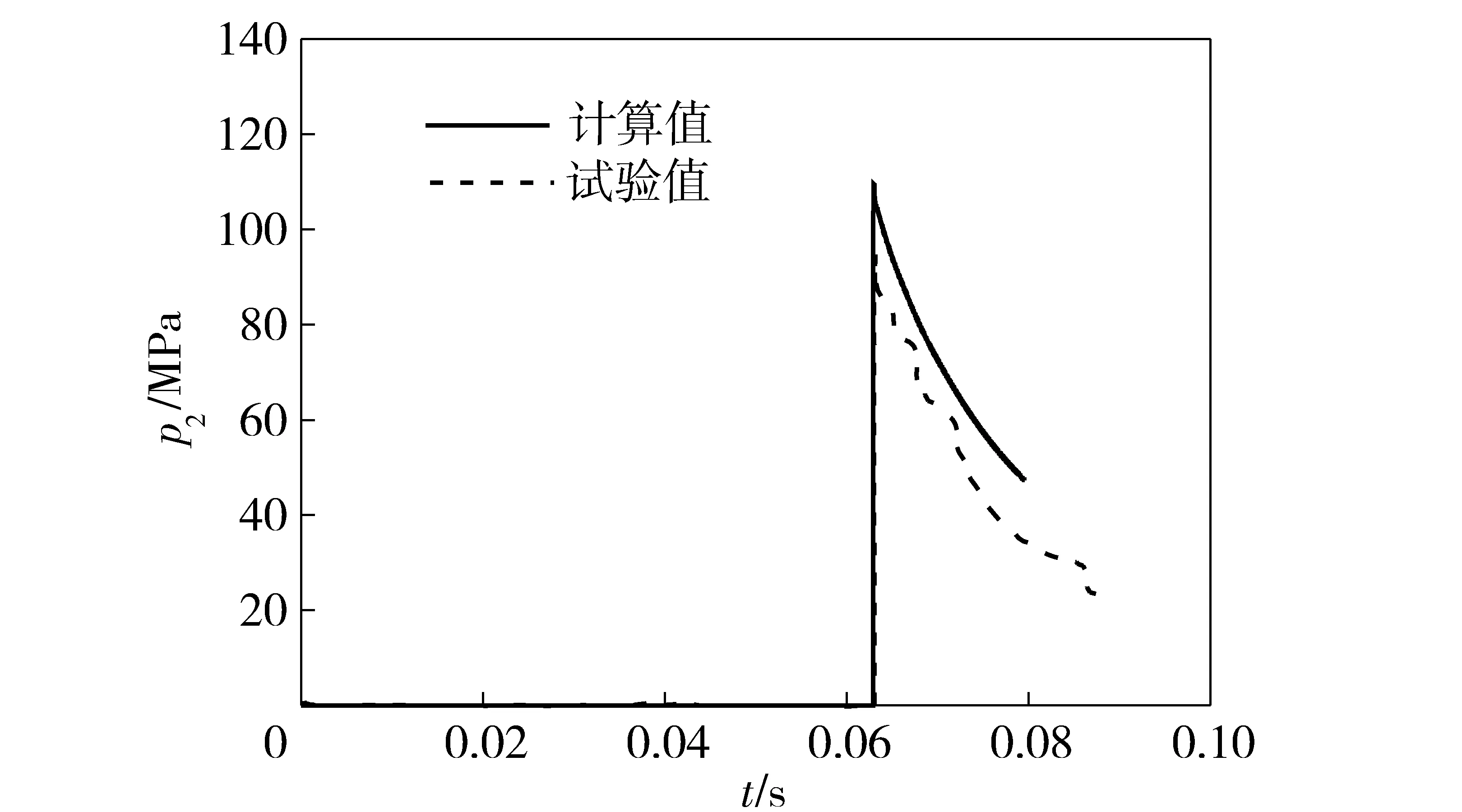
图8　第2发2号位置处压力曲线Fig.8　　　　Curves of calculated and experimental pressures at No.2 position (Test 2)

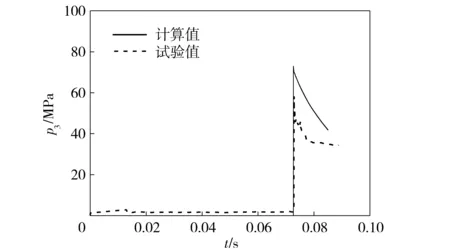
图9　第1发3号位置处压力曲线Fig.9　　　　Curves of calculated and experimental pressures at No.3 position (Test 1)

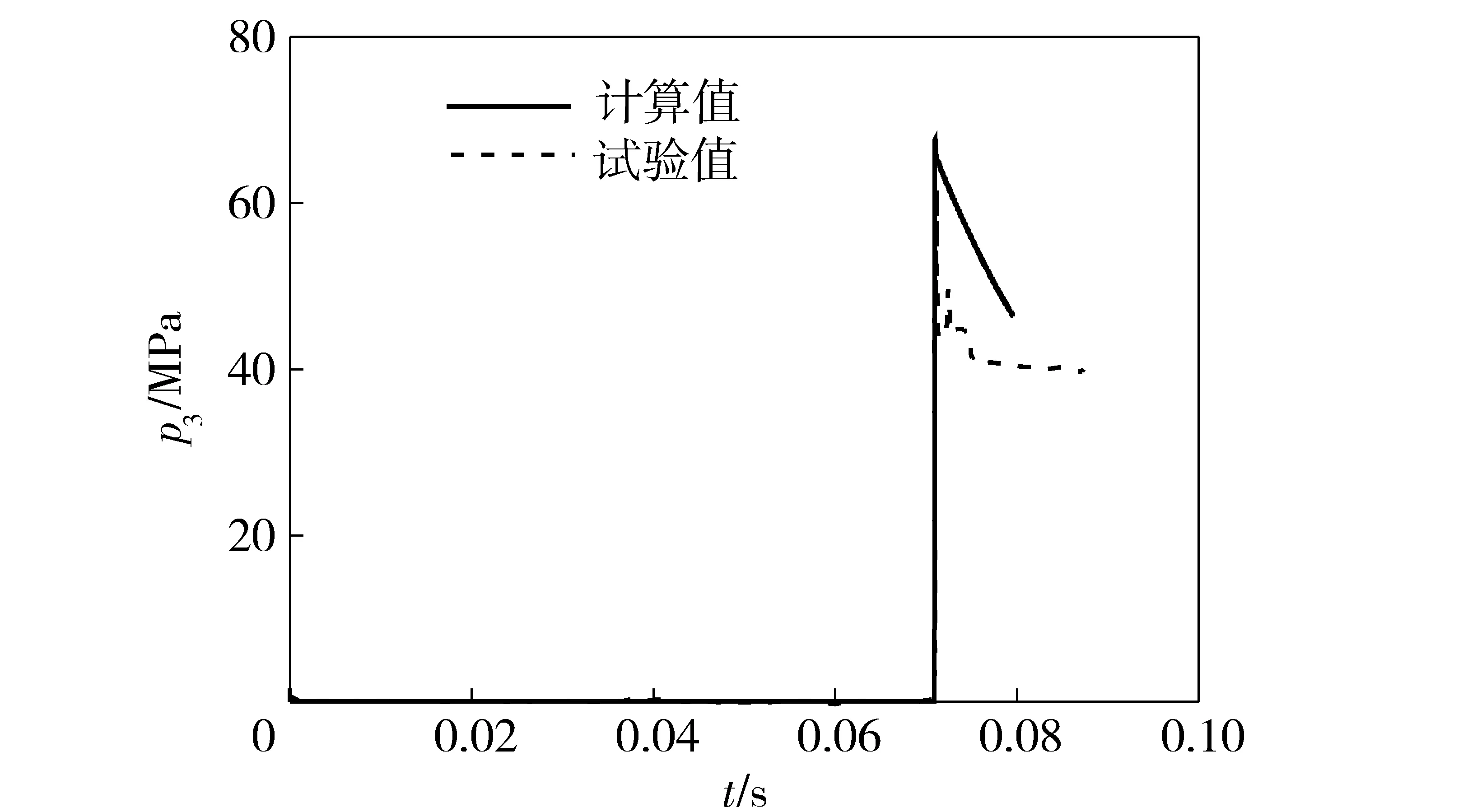
图10　第2发3号位置处压力曲线Fig.10　　　　Curves of calculated and experimental pressures at No.3 position (Test 2)

表1列出了计算和试验所得的弹丸初速v0和炮口压力p0情况。从表1可见：炮口压力计算值和试验值都较为接近；测试所得弹丸初速略微小于计算结果，这是由于在试验中，考虑到炮口火焰影响，炮口速度一般在离炮口一定距离处测得，因此略有减小。两发计算和试验皆得到弹丸先与平衡体出炮口。

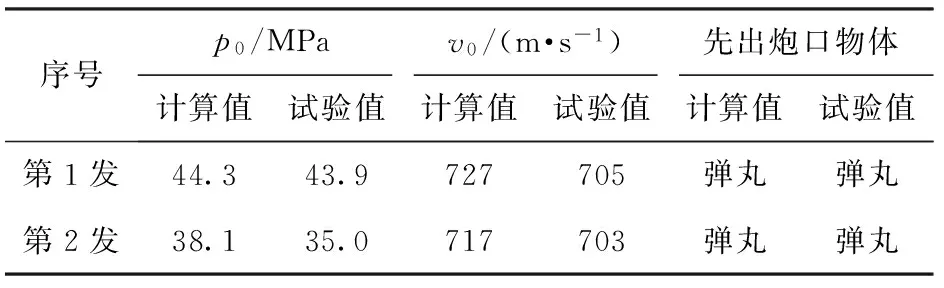
表1　计算结果和试验结果对比情况

从上面的分析可以看出，计算结果与实际结果拟合较好，计算结果较为可靠，选取第1发对内弹道性能作进一步研究。图11和图12为弹丸、平衡体启动前和启动后5个时刻中心轴附近的压力沿轴向的分布情况。弹丸约在0.012 61 s时启动，平衡体约在0.012 74 s时启动，二者几乎同时启动。从图11弹丸启动前的压力沿轴向分布曲线可以看出，初始时，从传火孔传出的气体迅速向两边扩散，由于左右两个固壁边界的存在，气体在固壁处堆积，引起两边压力略高于中间压力，产生了沿轴向的初始压力波。一部分气体碰撞壁面后反弹，从壁面向中央运动，在中间与新流入往两边扩散的气体汇合，又引起中间压力的上升。这样，由中间向两边和由两边向中间的气体逐渐混合，沿轴向的压力波逐渐被削弱。不得不提的是，这一过程的最大压差也只是在0.5 MPa左右。传火的均匀性，以及装药分布的均匀性，有效地减小了压力波。图12中，弹丸和平衡体启动后，由于弹丸质量小于平衡体质量，所以弹丸速度增加远快于平衡体速度增加，因此弹底压力较低，最大压力位置靠近平衡体端。火药约在0.06 s左右燃烧完毕。

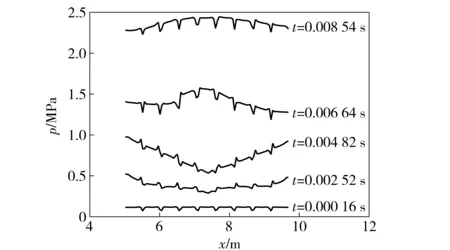
图11　初始5个时刻中心轴附近的压力沿轴向分布情况Fig.11　　　　Distribution of pressure along axial direction at the position near central axis

图12　7个时刻中心轴附近的压力沿轴向分布情况Fig.12　　　　Distribution of pressure along axial direction at the position near central axis

图13　初始5个时刻初始药室中部的压力沿径向分布情况Fig.13　　　　Distribution of pressure along radial direction in the center of initial chamber

图14　7个时刻初始药室中部的压力沿径向分布情况Fig.14　　　　Distribution of pressure along radial direction in the center of initial chamber

图13和图14为药室中心处压力pc沿径向的分布曲线，从中可以看出，初始时，由于点火气体的加入，向壁面扩散，壁面处压力略有升高。随着火药气体的燃烧，往中心轴位置去的压力逐渐升高，壁面的高压逐渐被削弱，逐步形成稳定的压力分布。火药燃烧完全以后，径向上的压力梯度完全消失，从0.065 92 s的压力曲线来看，从中心轴到壁面近乎平均分布。

图15和图16为两个时刻的空隙率沿轴向分布曲线。图15可以看出，传火初始时，药室内模块较为均匀的排布。图16为药室中部形成高压时，药束模块向两边运动，因此中间的空隙率较大。但是弹丸和平衡体打开前，药室中的压力波强度较小，药束模块运动较缓，所以并没有产生严重的堆积和挤压现象。图17时弹丸和平衡体已经运动了一段距离，空隙率的锯齿低值部分为药束模块所在位置，反映了药束模块的燃烧快慢，锯齿的低值分布情况与图12中对应的压力分布情况是一致的。 整个过程中，药束均未发生明显的堆积，模块化管状装药大大提升了火药分布的有序性，保证了发射的安全性。

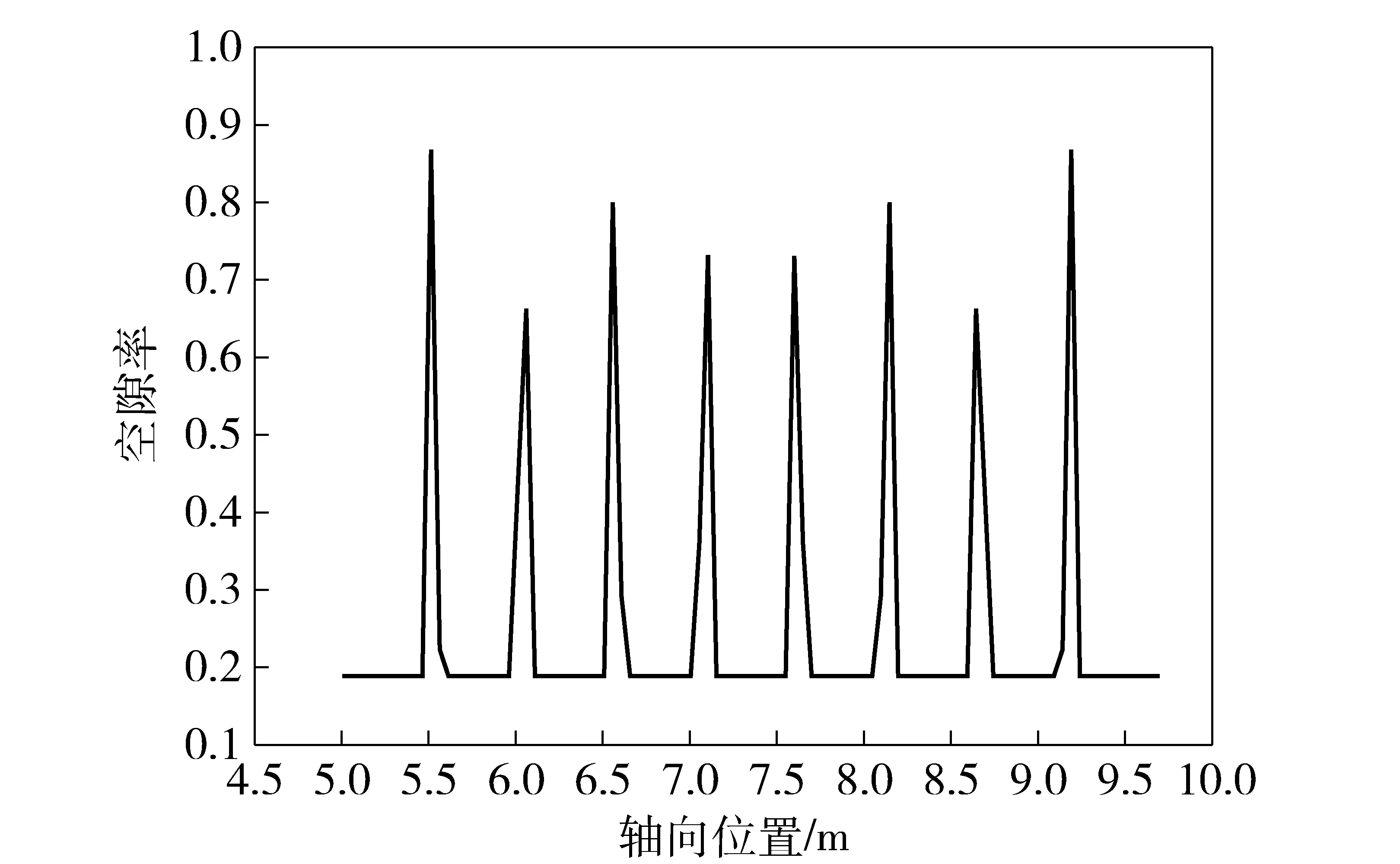
图15　　　　t=0.000 16 s时中心轴附近的空隙率沿轴向分布情况Fig.15　　　　Distribution of void ratio along axial direction at the position near central axis for t=0.000 16 s

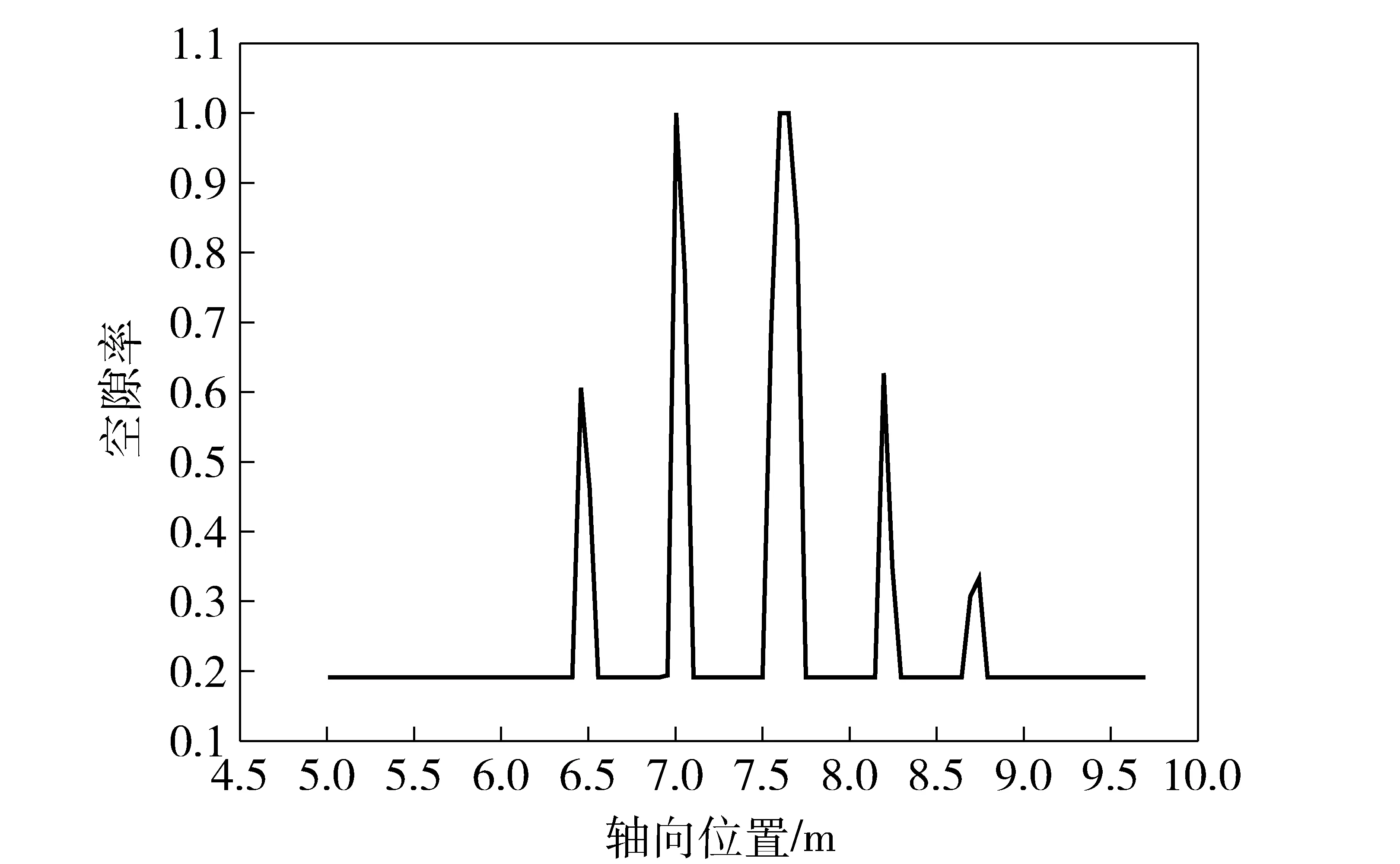
图16　　　　t=0.008 54 s时中心轴附近的空隙率沿轴向分布情况Fig.16　　　　Distribution of void ratio along axial direction at the position near central axis for t=0.008 54 s

图17　　　　t=0.056 61 s时中心轴附近的空隙率沿轴向分布情况Fig.17　　　　Distribution of void ratio along axial direction at the position near central axis for t=0.056 61 s

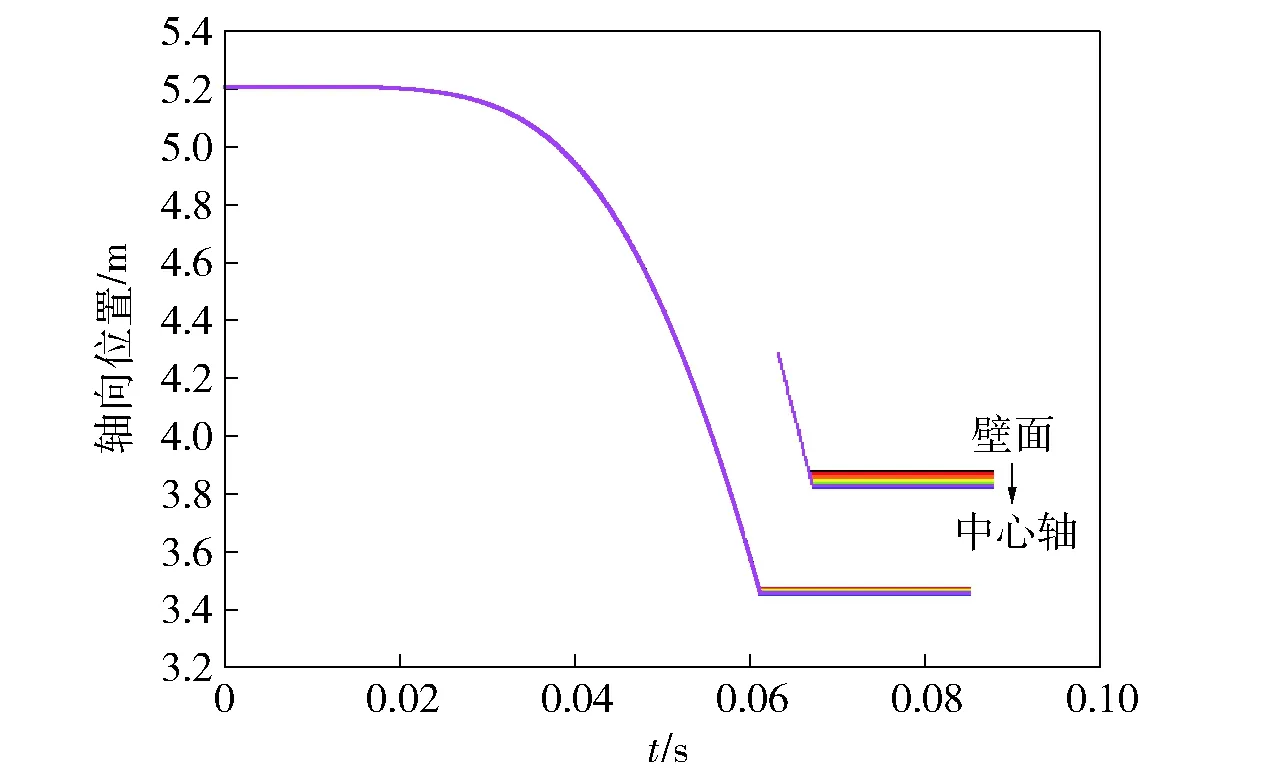
图18　　　　装药模块1中的药条在不同径向位置处沿轴向运动轨迹Fig.18　　　　Location curves of No.1 charge module at different axial positions

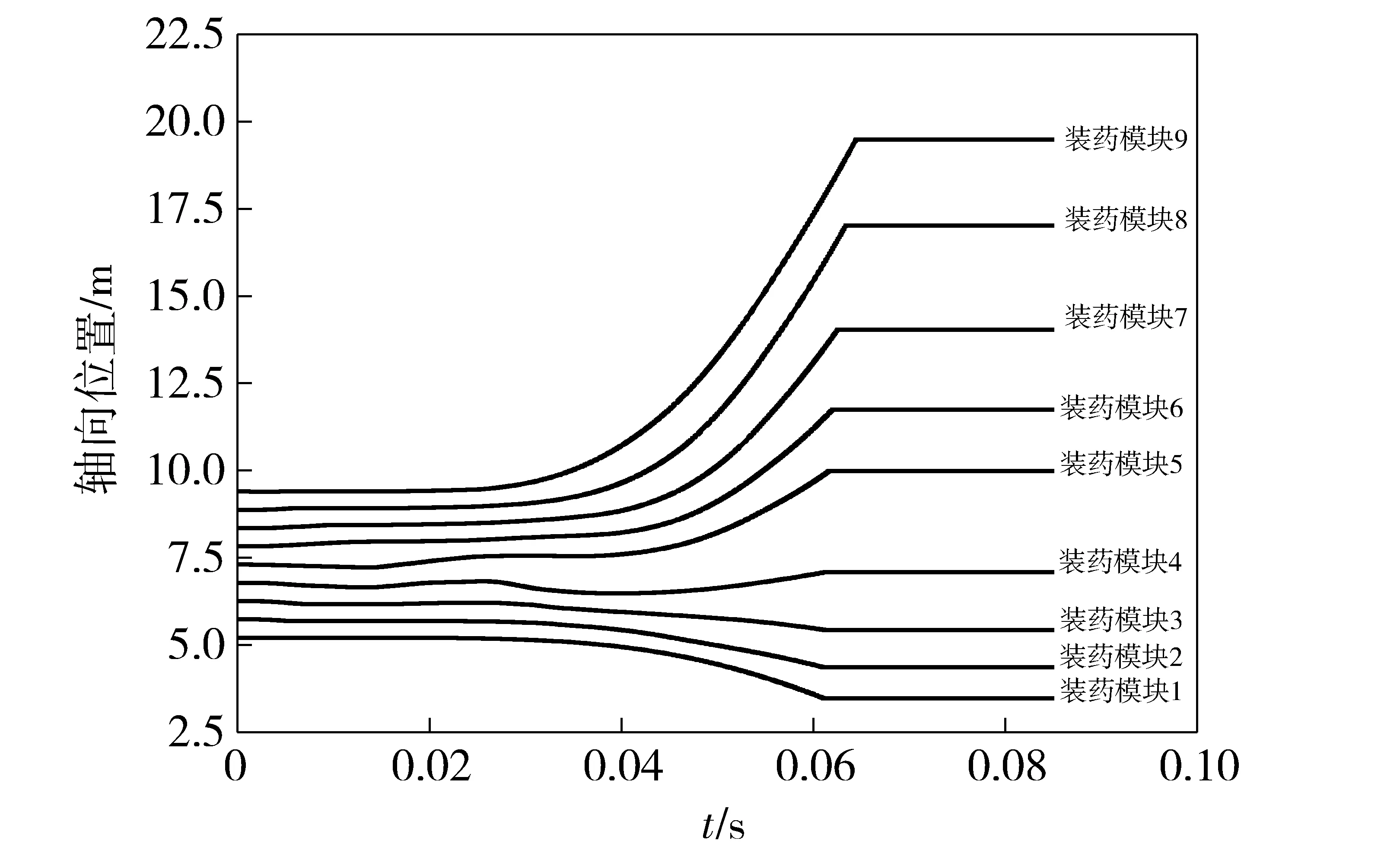
图19　中心轴附近的药条沿轴向运动轨迹Fig.19　　　　Location curves of 9 charge modules along axial direction near the central axis

图18和图19为药条的运动轨迹曲线。从图18中可以看出，同一个模块中不同径向位置上的药条运动轨迹基本相同,这说明相同轴向位置，不同径向位置处的压力差较为接近。不难想象，这是由于平衡炮口径与长度相比很小，所以轴向上的变化情况占主导地位。对图19进行分析，发射初始阶段，药条略微往两边运动，但是由于压力波的强度较弱以及药室空间有限，药条的运动是较为缓慢的。弹丸和平衡体启动后，由于弹丸运动速度较快，大部分的火药向弹底运动，还有少部分火药向平衡体底部运动，药条的运动随着弹丸和平衡体速度的加快而加快。整体上来说，采用模块化装填，药条运动有序，对降低火药撞击，提高发射稳定性是极为有利的。

4　结论

本文研究了管状药模块化装填的的大口径高速平衡炮，通过欧拉- 拉格朗日相结合的方法考虑气体与固体两相流动及相互作用，同时对管状药条提出在径向按线性排布的假设，建立了考虑管状药束轴向运动的二维内弹道模型，对某大口径平衡炮进行了数值模拟。数值模拟所得的压力变化趋势以及初速大小都与试验结果较为吻合，说明建立的数学模型有一定的合理性。通过对计算结果的进一步分析，得到了膛内火药气体分布以及药条运动规律。本文的工作对进一步研究大尺寸装药的火炮内弹道性能提供了新的手段。

References)

[1]徐流恩, 李永池, 高乐南. 大口径高速平衡炮发射安全性分析[J].中国科学技术大学学报, 2008, 38(11):1304-1309.

XU Liu-en, LI Yong-chi, GAO Le-nan. Shooting security analysis of counter-mass propelling gun with large caliber and high muzzle velocity[J]. Journal of University of Science and Technology of China, 2008, 38(11):1304-1309.(in Chinese)

[2]陶如意, 孙继兵, 黄明, 等. 高低压平衡炮内弹道数值模拟及试验研究[J]. 南京理工大学学报, 2006, 30(4):478-481.

TAO Ru-yi, SUN Ji-bing, HUANG Ming, et al. Interior ballistics numerical simulation and experiment on balance gun with low and high pressure chamber[J]. Journal of Nanjing University of Science and Technology, 2006, 30(4):478-481.(in Chinese)

[3]贠来峰, 芮筱亭, 冯可华. 对某平衡炮高、低温内弹道性能异常的分析[J]. 火炸药学报, 2009, 32(2):68-71.

YUN Lai-feng, RUI Xiao-ting, FENG Ke-hua. Analysis of abnormal interior ballistic performance of an equilibrium launcher at high and low temperature[J]. Chinese Journal of Explosives and Propellants, 2009, 32(2):68-71.(in Chinese)

[4]蒋淑园, 季晓松, 王浩, 等. 大口径长药室平衡炮发射装药多点点火特性[J]. 含能材料, 2015, 23(5):477-483.

JIANG Shu-yuan, JI Xiao-song, WANG Hao, et al. Multi-point ignition characteristics in large caliber balance gun propellant with long-chamber charges[J]. Chinese Journal of Energetic Materials, 2015, 23(5):477-483.(in Chinese)

[5]徐流恩, 李永池, 高乐南. 大口径高速平衡炮不同发射药应用探讨[J]. 弹道学报, 2009, 21(2):15-18.

XU Liu-en, LI Yong-chi, GAO Le-nan. The application discussion of propellant in large caliber and high speed counter-mass propelling gun[J]. Journal of Ballistics, 2009, 21(2):15-18.(in Chinese)

[6]王明东, 王天祥. 新概念武器的现状与发展趋势[J].四川兵工学报, 2014, 35(6):1-5.

WANG Ming-dong, WANG Tian-xiang.Actuality and development trend of new concept weapon [J]. Journal of Sichuan Ordnance, 2014, 35(6):1-5.(in Chinese)

[7]程诚, 张小兵. 某制导炮弹二维两相流内弹道性能分析与数值模拟研究[J]. 兵工学报, 2015, 36(1):58-63.

CHENG Cheng, ZHANG Xiao-bing. Two-dimensional numerical simulation on two-phase flow interior ballistic performance of a guided projectile[J]. Acta Armamentarii, 2015, 36(1):58-63.(in Chinese)

[8]孙晨, 陈凌珊, 汤晨旭. 气固两相流模型在流场分析中的研究进展[J].上海工程技术大学学报, 2011, 25(1):49-53.

SUN Chen, CHENG Ling-shan, TANG Chen-xu.Study and deve-lopment of gas-solid two-phase flow model in flow field analysis[J]. Journal of Shanghai University of Engineering Science, 2011, 25(1):49-53.(in Chinese)

[9]张博孜, 王浩, 王珊珊, 等. 大口径平衡炮内弹道一维两相流建模与仿真[J]. 弹道学报, 2014, 26(1):17-21.

ZHANG Bo-zi, WANG Hao, WANG Shan-shan, el al. One-dimensional two-phase flow modeling and simulation for interior ballistics of large-caliber Davis gun[J]. Journal of Ballistics, 2014, 26(1):17-21.(in Chinese)

[10]袁亚雄, 杨均匀. 内弹道分散颗粒模型及数值计算[J].兵工学报, 1996, 17(3):198-201.

YUAN Ya-xiong, YANG Jun-yun. An interior ballistics discrete particle model and its numerical calculation[J]. Acta Armamentarii, 1996, 17(3):198-201.(in Chinese)

[11]周彦煌, 王升晨. 实用两相流内弹道学[M]. 北京:兵器工业出版社, 1990.

ZHOU Yan-huang, WANG Sheng-chen. Applied two-phase flow interior ballistics[M]. Beijing: Publishing House of Ordnance Industry, 1990.(in Chinese)

[12]袁亚雄, 张小兵. 高温高压多相流体动力学基础[M]. 哈尔滨:哈尔滨工业大学出版社, 2005.

YUAN Ya-xiong, ZHANG Xiao-bing. Basic high temperature and high pressure multiphase fluid dynamics[M]. Harbin: Harbin Institute of Technology Press, 2005.(in Chinese)

[13]翁春生, 王浩.计算内弹道学[M]. 北京:国防工业出版社, 2006.

WENG Chun-sheng, WANG Hao. Computational interior ballistics[M]. Beijing: National Defense Industry Press, 2006.(in Chinese)

Establishment and Simulation of Two-dimensional Interior Ballistics Model of Large Caliber Davis Gun Considering the Axial Movement of Tubular Charge Clusters

JIANG Shu-yuan, WANG Hao, LIN Chang-jin, WANG Jin-long

(School of Energy and Power Engineering, Nanjing University of Science and Technology， Nanjing 210094, Jiangsu, China)

Considering that the length of the tubular charge for the large caliber high speed Davis gun is long, the traditional pseudo-fluid hypothesis in two-phase flow model may cause errors. In order to solve this problem, Eulerian coordinate system is used to settle the gas field, and the Lagrangian coordinate system is used to settle the solid field. It is assumed that the tubular charge clusters are linearly configured along radial direction, these clusters move along axial direction，and gas moves along radial and axial directions. Based on this assumption, a two-dimensional interior ballistics model is established for a 480 mm Davis gun with tubular modular charge. Then through the comparison of the simulated and experimental results, the proposed model is verified to be effective. The distribution of gas pressure along two directions and the movement rules of tubular charge clusters along axial direction were obtained by further analysis of the simulated results.

ordnance science and technology; Davis gun; interior ballistics; two-phase flow; numerical simulation

2015-11-04

蒋淑园(1988—)，女，博士研究生。E-mail:jiangshuyuan910@126.com；

王浩(1961—)，男，研究员，博士生导师。E-mail:wanghao@ mail.njust.edu.cn

TJ012.1.1+1

A

1000-1093(2016)10-1941-08

10.3969/j.issn.1000-1093.2016.10.022