弯曲型导电聚合物驱动器逆模型控制*
刘怀民,王湘江,尚星良
(南华大学机械工程学院,湖南衡阳421001)
弯曲型导电聚合物驱动器逆模型控制*
刘怀民,王湘江*,尚星良
(南华大学机械工程学院,湖南衡阳421001)
针对三层弯曲型导电聚合物驱动器,研究了一种无需外部传感反馈装置的逆模型控制方法。通过实验辨识获得驱动器系统传递函数准确,以驱动器系统的4阶传递函数建立的逆模型控制系统结构简单、易于实现。通过补偿驱动器位移漂移特性提高位移控制精度。实验结果表明:其所提出的具有位移漂移补偿的逆模型控制位移输出能够快速有效地跟踪驱动器的实际位移响应,同时精度符合控制要求。
生物传感器;导电聚合物驱动器;系统辨识;逆模型控制
EEACC:7230doi:10.3969/j.issn.1004-1699.2016.10.010
电活性聚合物(EAPs)是一类新型并极具发展潜力的智能材料。该类聚合物材料具有驱动电压低、良好的生物适应性、能在空气或液体介质的环境下工作;某些类型的电活性聚合物能够在电流或电场作用下产生可逆物理形变,这种可逆物理形变特性与动物肌肉极为相似,被公认为是最合适的仿肌肉材料[1-2]。此外,基于电活性聚合物的驱动器产生较大应力应变能使其很好地取代传统驱动器技术,特别是在小尺寸(微米级或纳米级)限制要求情况下,传统驱动装置如电机、螺线管、液压装置等将失去原有功能,而电活性聚合物材料依然能够发挥作用。因此,在仿生微操作系统、仿生机器人、生物医学设备和生物传感器等领域具有广泛的应用前景[3-6]。但是,此类电活性聚合物材料也存在非线性特点(如迟滞、漂移等现象)影响其位置精度与性能。
在众多类型的电活性聚合物中,基于导电聚吡咯(PPy)制备而成的三层弯曲型导电聚合物驱动器因其良好的生物相容性而且能在空气与液体介质环境下较稳定工作,因而受到广泛关注。Smela等[7]采用聚吡咯驱动器制备出导电聚合物血管连接器,缩短了手术过程中血管拼接所需时间,从而将导电物驱动器应用于生物医学领域。然而将这类导电聚合物驱动器应用于生物医学及仿生领域需要采用内置传感器或外置反馈装置,就目前的技术手段还无法达到将传感器与导电聚合物驱动器集成在一起并能稳定工作的要求;采用外置反馈装置尺寸远大于导电驱动器本身尺寸,无法实现其在生物医学等领域的应用。应用于微/纳米机构驱动时,随着驱动器数量和自由度的增加,使用传感器反馈控制将不切实际。一种简单、有效实现该类型驱动器无传感反馈控制的方法是采用逆模型控制。该方法基于逆系统方法为对象设计逆模型控制系统,用被控对象传递函数的逆模型作为串行控制器来开环控制系统的动态性能,可以有效地避免反馈引起的系统不稳定现象[8]。本文通过建立驱动器位移测控系统进行实验获取导电聚合物驱动器系统的频率响应数据,根据频率响应数据辨识出系统传递函数参数从而建立驱动器的逆模型。并在此逆模型基础上对影响驱动器位置精度的漂移现象进行补偿,对驱动器动态位移响应控制性能进行了实验验证。
1 驱动器材料及实验装置
1.1驱动器结构及其工作原理
实验采用的弯曲型导电聚合物驱动器为五层层状结构:多孔隙聚偏二氟乙烯(PVDF)膜用作基体材料可以储存离子液并对两外层聚吡咯起隔离作用;两外层为导电聚合物聚吡咯(PPy),工作过程发生可逆氧化还原反应产生体积膨胀或收缩;PVDF膜两表面通过离子注入的方法镀有一层极薄的黄金层,用于电化学沉积PPy并增加导电性;整个结构如同一端受约束另一端自由弯曲的悬臂梁结构。驱动器结构示意如图1所示,其横截面显微结构如图2所示。
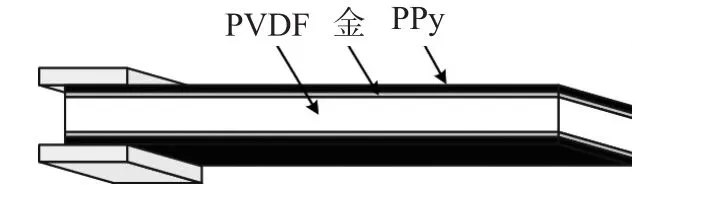
图1 导电聚合物驱动器结构图

图2 三层弯曲型驱动器横截面结构显微图
该类型弯曲型导电聚合物的驱动器工作原理在文献[9]进行了详细说明。当两外层PPy层通过电极加载电压,电势差导致PVDF膜中储存的Li+TFSI-/PC离子液(二三氟甲基磺酰亚胺电解质锂盐,碳酸丙烯酯PC为有机溶剂)中阴阳离子发生迁移,正电极端PPy吸收阴离子发生氧化反应膨胀,负电极端PPy发生还原反应引起PPy收缩。膨胀与收缩程度差异造成驱动器的弯曲运动,驱动器弯曲运动示意如图3所示。
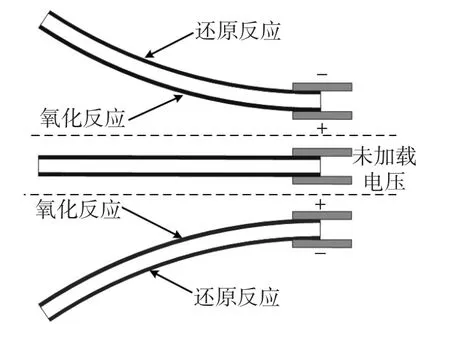
图3 驱动器弯曲运动示意图
图4为尺寸10 mm×2 mm驱动器在1 V电压下的弯曲运动响应。

图4 尺寸10 mm×2 mm驱动器弯曲运动
1.2驱动器位移测控系统
驱动器位移测控实验装置如图5与图6所示。其中具有高测量精度和响应速度的非接触式激光位移传感器(SENSOPART,FT 50 RLA-40-F-L4S)用于驱动器位移响应测量。使用高速摄相机(FASTEC)采集图像和分析。激光位移传感器固定于XY轴手动位移平台上(调节范围±10 mm,精度0.5 μm)。驱动器驱动电压信号通过Simulink建模生成,由高速模拟量输出卡(Advantech,PCI-1721)D/A通道输出电压信号经电极加载于两PPy层,激光位移传感器将采集到驱动器位移变化值转化为电压信号经数据采集卡(Advantech,PCI-1710U)A/D通道输入计算机,并由Matlab/Smulink记录测量数据。
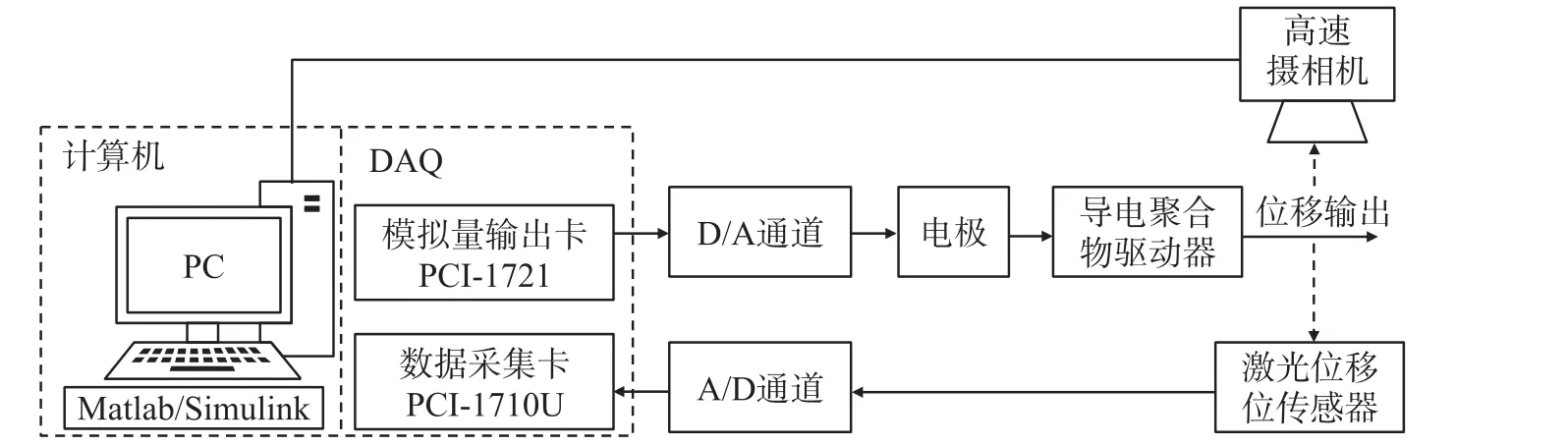
图5 位移测控系统示意图
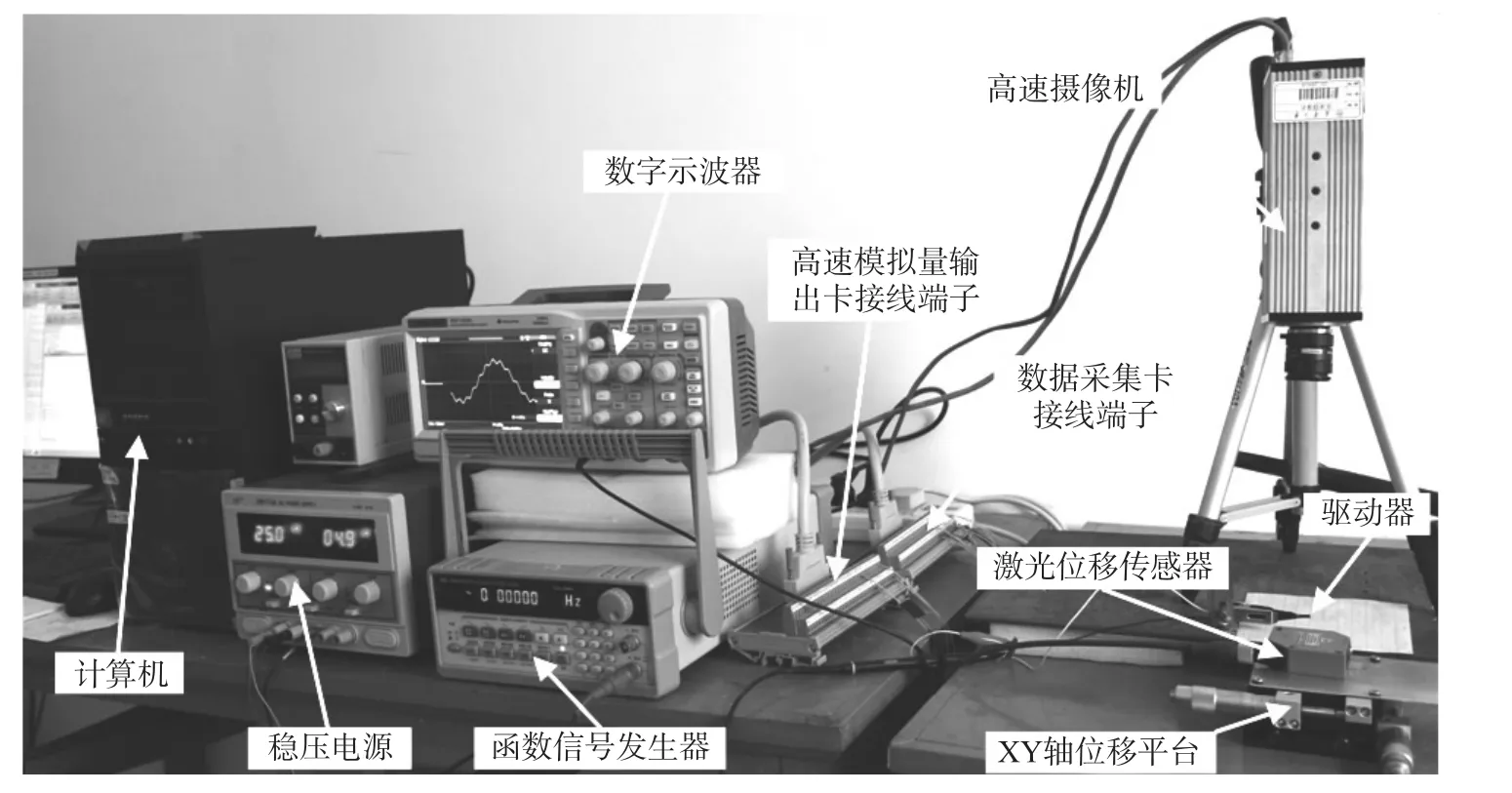
图6 位移测控系统实验装置
实验所用驱动器材料尺寸为10 mm×2 mm,开始实验测试之前在浓度为0.5 mol/L的Li+TFSI-/PC离子液(PC为碳酸丙烯酯试剂)中浸泡1 h(能确保驱动器连续稳定工作数小时),数据采样周期设为0.002 s。传感器输出电压信号已标记为1 V/mm,记录数据之前驱动器运行10 min。激光位移传感器光斑焦点距夹钳端8 mm(有效长度)。
2 驱动器逆模型
2.1逆模型控制原理
采用逆系统方法为对象设计逆模型控制系统的基本思想是利用已辨识出的被控对象G(s)的逆动态模型G-1(s)作为控制器,将其串联在被控对象之前,使等效传递函数为1,实现线性化控制[10]。对单输入/单输出(SISO)系统Σ,设输入、输出为u(t)、y(t),初始状态为x0。记描述映射关系的算子为G,则y(t)=u(t)G。若存在另一SISO系统Σ′,输入为φ(t),输出为u(t),φ(t)为某区域内的任意连续函数,取φ(t)=y(a)(t),即α阶导数,设映射关系算子为G-1,如果满足:
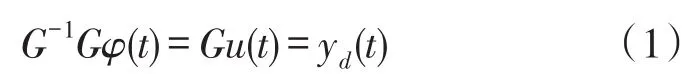
则当α=0时,称系统Σ′为原系统的单位逆系统。式(1)中yd为y的给定值。弯曲型导电聚合物驱动器的逆模型可以看作是电压输入与位移输出的“倒置”,因此需要对驱动器的输入输出之间的关系有一个清晰的认识。考虑给定电压输入与相应位移响应,就可以把驱动器看作是一个单输入单输出的模型。模型输入为加载电压信号,输出为驱动器的尖端位移。
2.2驱动器系统传递函数辨识
建立驱动器的逆动态模型G-1(s)首先需对驱动器系统的传递函数进行辨识。由于导电聚合物驱动器系统,其复杂机理和内部变化规律并未完全掌握,采用“黑箱”技术建模对于大多数没有准确理论描述的解构与器件是一种常用的方法,也是行之有效的方法。通过建立导电聚合物驱动器系统的“黑箱”模型,对这个“黑箱”进行频率特性测试,用一定幅值、不同频率的正弦信号作输入,考察其稳态输出[11]。不同频率的正弦输入信号由计算机经高速模拟量输出卡D/A通道加载于驱动器,驱动器在电压信号的作用下发生弯曲运动,采集并记录激光位移传感器的输出。驱动器频率特性测试原理框图如图7所示。
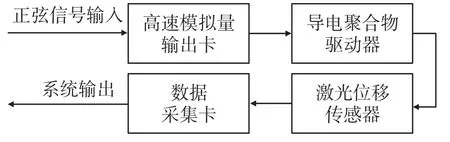
图7 驱动器频率特性测试原理框图
根据实验获取的驱动器系统开环频率特性(输出和输入谐波的幅值比与相位差)计算实频特性Re(ω)和虚频特性Im(ω),采用Levy法来辨识驱动器系统传递函数参数。该方法采用由频率特性数据序列直接拟合系统传递函数参数,通过极小化模型与测试数据之间的误差准则函数来确定模型的参数[12]。根据Nguyen等[13]结论,弯曲型导电聚合物驱动器系统可简化为n阶传递函数:
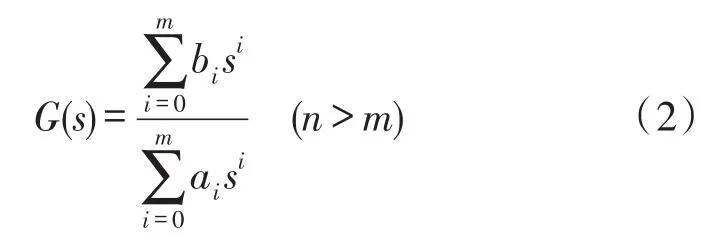
式中,传递函数系数ai、bi由驱动器的尺寸、离子扩散系数、驱动器的应力应变比决定。利用Matlab软件对驱动器系统的实、虚频特性数据进行处理。通过递阶辨识,先辨识低频环节,得出结果后从频率特性数据中修正掉已辨出的低频环节,然后按同样的方法进行中、高频环节的辨识。最后,将各个低阶子系统相乘,便得到了完整的系统传递函数。经Levy法辨识所得2、4、6阶传递函数系数见表1所示。根据传递函数绘制频率响应曲线如图8所示。
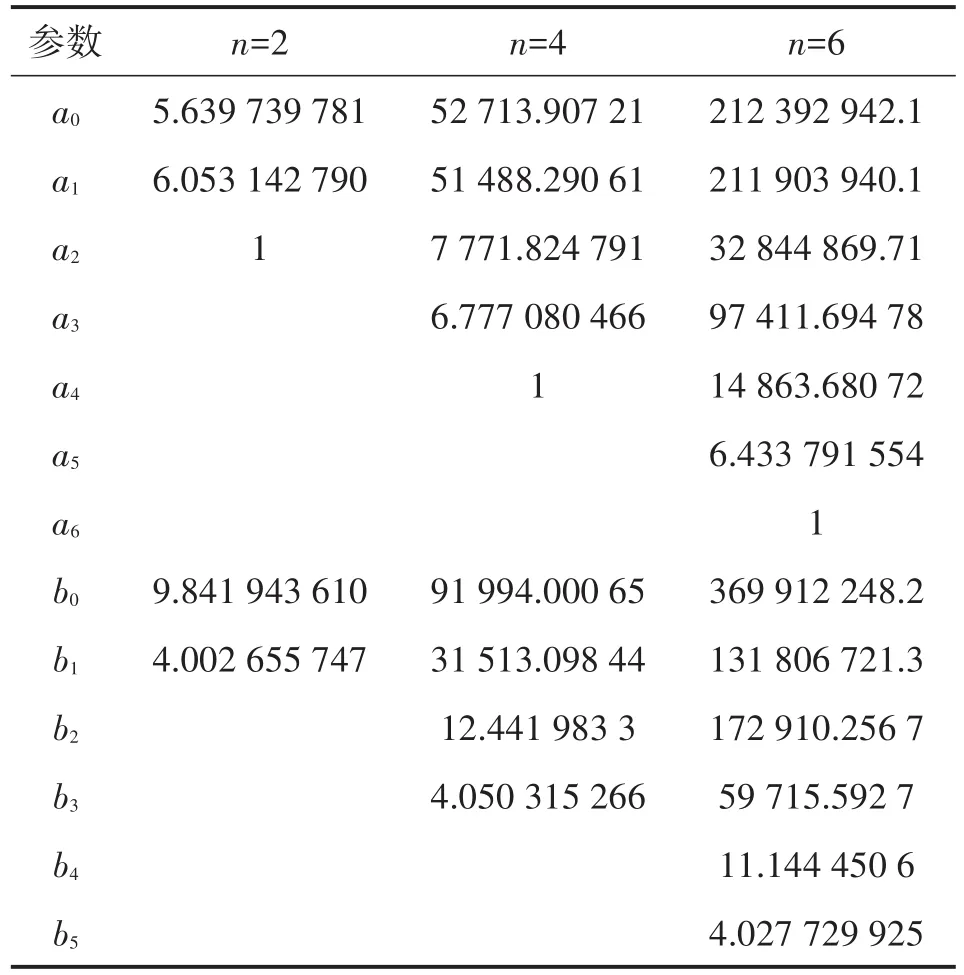
表1 辨识所得传递函数系数

图8 辨识所得传递函数频率响应曲线
2.3逆模型的建立
辨识出尺寸为10 mm×2 mm驱动器传递函数G(s)之后,验证传递函数的所有零点和极点是否都在复平面[s]左半平面内,即是否为最小相位系统。对于最小相位系统通过交换其零点与极点,增益取倒数可直接获得G(s)的逆动态模型G-1(s)。上述辨识所得N=2、4阶传递函数零极点都在复平面[s]左半平面内,N=6阶传递函数在复平面[s]右半平面内存在零点。本文以驱动器的4阶传递函数为例计算G-1(s)建立逆模型。驱动器4阶传递函数零极点如表2所示。
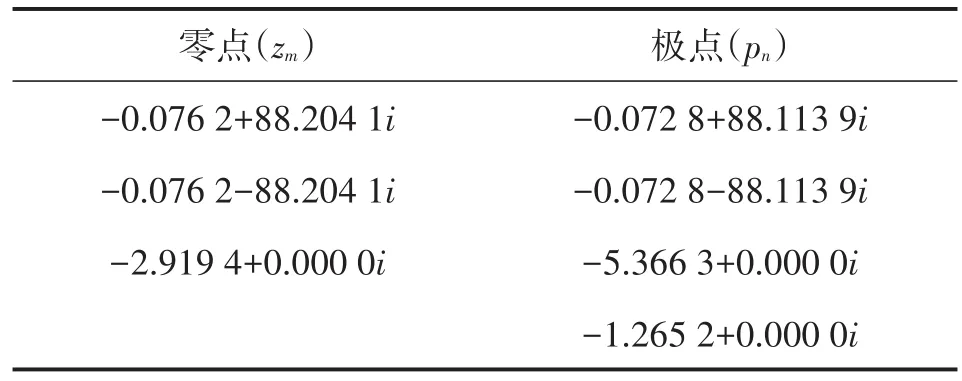
表2 10 mm×2 mm驱动器4阶传递函数零极点
由于驱动器的4阶传递函数极点数大于零点数,经过逆变换所得G-1(s)的零点数大于极点数,其在高频段会产生无限增益,因此需增加低通滤波器来限制G-1(s)在高频段增益保持系统稳定。采用贝塞尔(Bessel)滤波器能在特定的频率范围内,有近似的线性时延(或相位)特性和较平坦的幅度特性,能在通带上保持被过滤的信号波形的特点,不会对G-1(s)的动态特性产生明显影响。利用Matlab中的函数[b,a]=besself(n,ωn)设计一个n阶截止频率为ωn弧度/秒的模拟贝塞尔滤波器。滤波器传递函数系数分别放在n+1维向量a和b中。其传递函数表达式为:
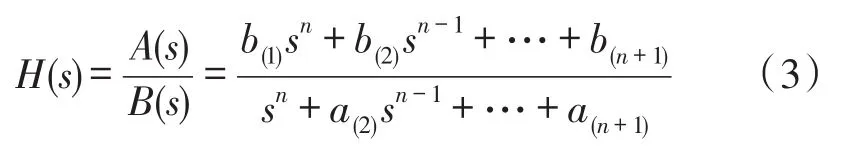
贝塞尔滤波器的幅度响应在截止频率小于3 dB,且随着阶数增大,衰减越大。当n=2,ωn=10 Hz时,可得到2阶截止频率为10 Hz的贝塞尔低通滤波器传递函数为:
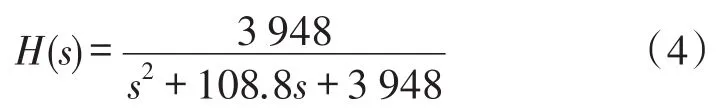
驱动器传递函数G(s)、逆动态模型G-1(s)、增加2阶截止频率为10 Hz的贝塞尔低通滤波器H(s)G-1(s)频率响应如图9所示。
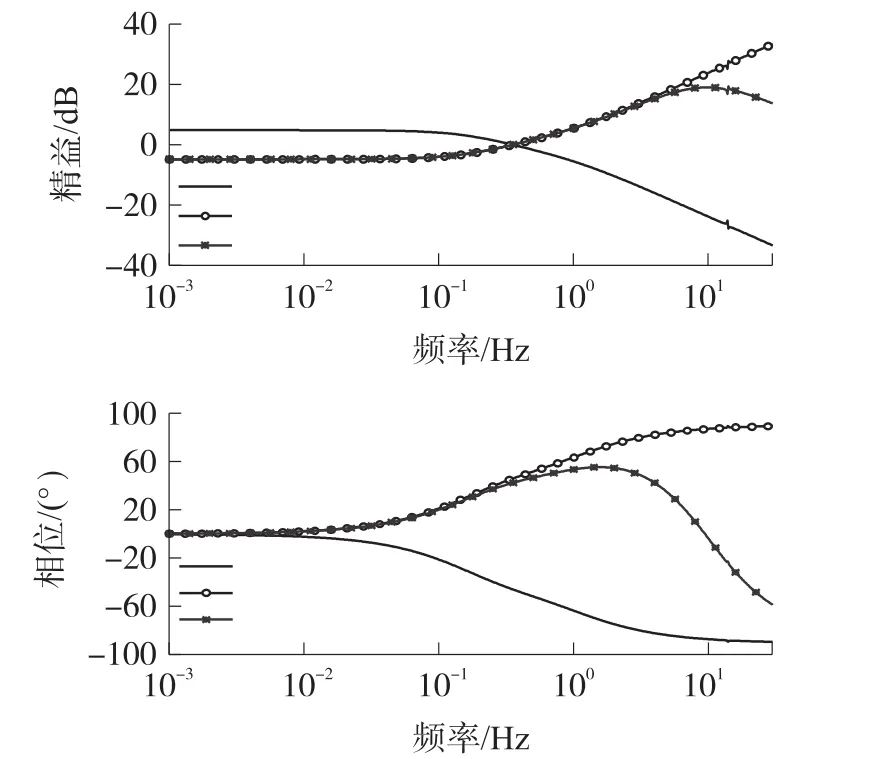
图9 G(s)、G-1(s)及H(s)G-1(s)频率响应
建立准确的逆控制模型还需对驱动器非线性特性(迟滞与漂移现象)引起的位置精度误差进行补偿。三层弯曲型导电聚合物驱动器因其具有对称结构使其在输入信号频率较低时位移迟滞现象并不显著,几乎可以忽略不计,但位移漂移现象对驱动器位置精度影响较大[14]。对于驱动器准静态和低频位移漂移可采用Kelvin-Voigt粘弹性模型表示[15]。该模型可简化为由弹簧和阻尼元件构成系统,如图10所示。
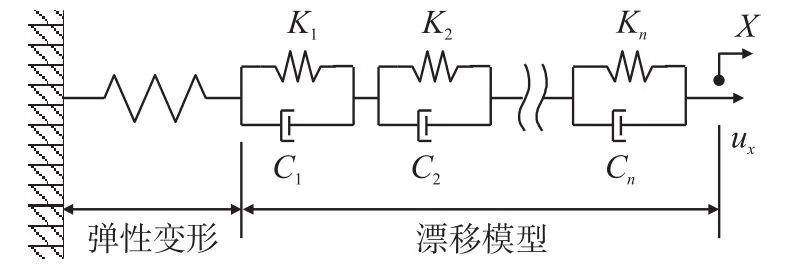
图10 粘弹性漂移模型
漂移模型系统的传递函数为:
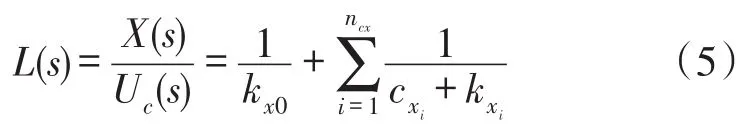
此处,X(s)与UC(s)分别为拉普拉氏域(Laplace)内x方向位移响应与输入电压。kx0表示低频弹性特性,ncx表示模型阶数(弹簧-阻尼元件的数量),通过选取合适的阶数可使模型的误差控制在合理范围。随着输入信号频率的增大,主要考虑动态响应过程中相对驱动器零点位置(初始位置)漂移对控制精度的影响。由于驱动器制备工艺不稳定性造成驱动器两外层PPy和镀金层均匀性及厚度的差异会对动态零点漂移产生比较大的影响,因此需通过实验测得零点漂移值,并在逆模型结合零点漂移算子进行位移漂移补偿,图11为实验所测零点漂移值随频率变化情况。
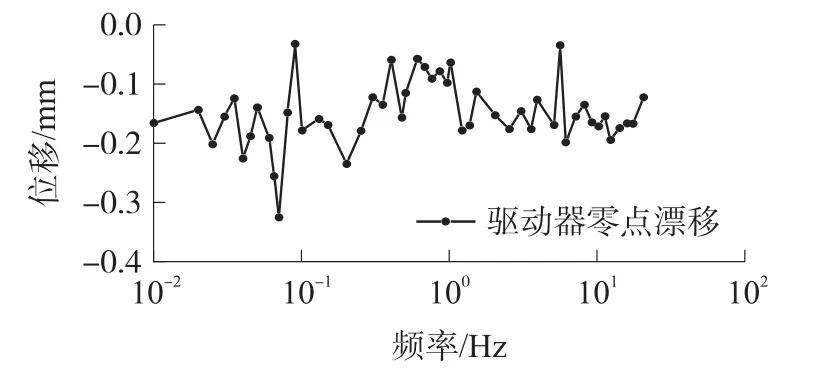
图11 动态零点漂移值随频率变化
考虑位移漂移补偿驱动器逆模型控制示意如图12所示。在拉普拉氏域(Laplace)内,驱动器系统输入与输出、理想输出位移与产生理想输出位移输入信号之间存在如下关系式。

已知系统理想位移输出信号YD(s)可通过上述公式计算获得产生理想位移输出的输入信号U(s)。

图12 驱动器逆模型控制示意图
3 驱动器逆模型实验验证
利用Matlab/Simulink工具模块搭建出如图12对应驱动器逆模控制模型。根据表2与式(4)及漂移值设置相应模块的参数,进行仿真。图13为驱动器施加阶跃输入信号(幅值为1 V)位移响应与逆模型控制结果及其误差比较。由图可知采用Kelvin-Voigt粘弹性模型能够有效地补偿驱动器准静态位置漂移误差。
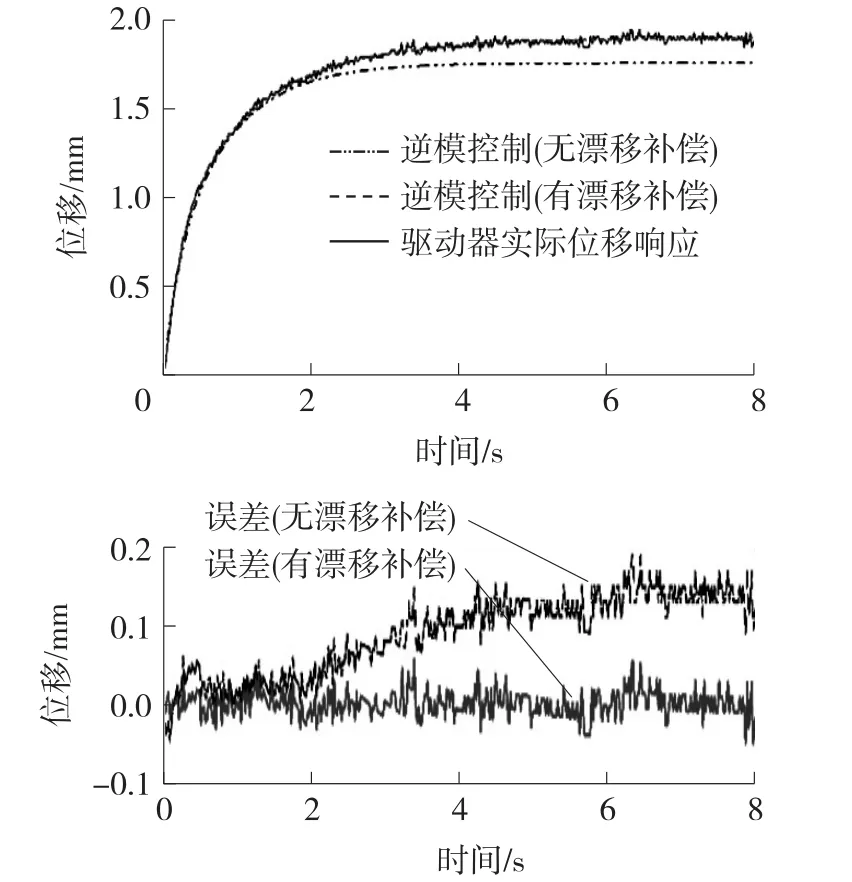
图13 驱动器位移响应与逆模型控制结果比较(阶跃信号幅值为1 V)
图14为驱动器施加正弦输入信号(yi=sin(0.1× 2πt))驱动器的实际位移响应与逆模型控制结果比较。从图可知增加零点漂移算子进行位移漂移补偿后的逆模型期望位移输出结果与驱动器的实际位移输出之间的误差非常小,具有零点漂移补偿逆模型期望位移输出能够很好地跟踪驱动器的实际位移输出。
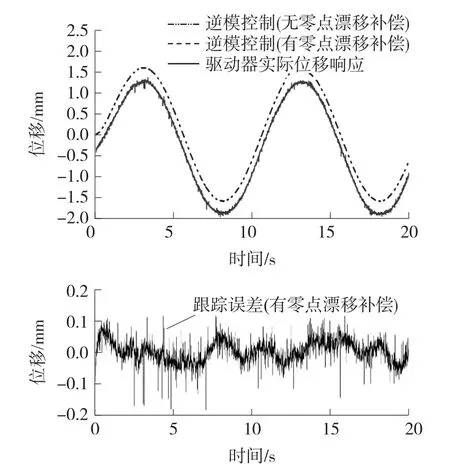
图14 驱动器位移响应与逆模型控制结果比较(f=0.1 Hz正弦输入信号)
图15为输入信号频率增至0.5 Hz,即yi=sin(0.5× 2πt),驱动器的实际位移响应与逆模型控制结果比较。随着正弦输入信号频率的增大,逆模型期望位移输出与实际位移输出之间的误差相应增大。其原因在于逆模型增加了滤波器对低频信号影响较小。另外,由于驱动器内电解质液的挥发作用和环境条件改变引起驱动器参数变化及激光位移传感器噪声也会对实验结果产生影响。
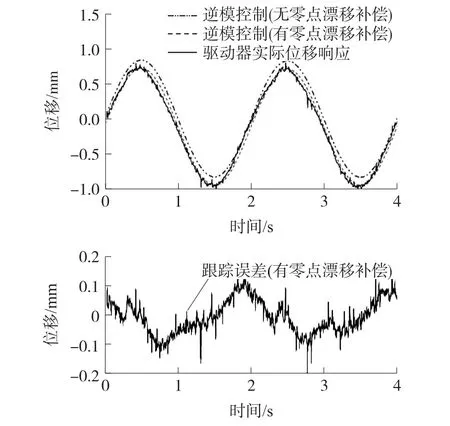
图15 驱动器位移响应与逆模型控制结果比较(f=0.5 Hz正弦输入信号)
通过比较多频率正弦输入信号驱动器实际位移响应与逆模型动态位移控制结果来验证逆模型的动态位移响应性能。图16与图17输入信号分别为:
A:yi=sin(0.05×2πt)+0.5×sin(0.5×2πt)
B:yi=0.8×sin(0.1×2πt)+0.2×sin(0.5×2πt)
驱动器实际位移响应与逆模型控制系统期望位移输出结果比较。

图16 驱动器位移响应与逆模型控制结果比较A

图17 驱动器位移响应与逆模型控制结果比B
为了定量反映具有位移漂移补偿逆模型控制精度可通过式(7)可计算获得上述输入控制信号位移响应均方根(RMS)误差,如表3所示。
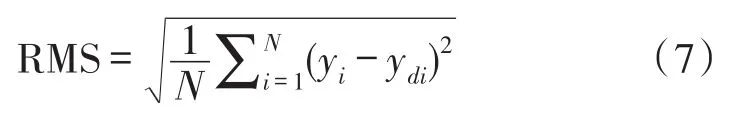

表3 输入控制信号位移响应均方根(RMS)误差
根据多频率正弦输入信号位移响应均方根误差及图16与图17逆模型控制跟踪结果可知,所建立的逆模型控制能快速有效地控制驱动器位移变化,其动态性能好、跟踪精度较高。
4 结论
本文针对三层弯曲型导电聚合物驱动器提出了一种无需外部传感反馈装置的逆模型控制方法。通过实验辨识获得驱动器系统传递函数准确,以驱动器系统的4阶传递函数建立的逆模型控制系统结构简单、易于实现。通过补偿驱动器位移漂移特性提高位移控制精度。实验结果表明:所提出的具有位移漂移补偿的逆模型控制位移输出能够快速有效地跟踪驱动器的实际位移响应,同时精度符合控制要求。由于驱动器系统存在参数不稳定因素容易引起所建逆模型无法产生准确的输入信号,当输入中高频信号时滤波器及迟滞现象等会造成逆模型期望位移输出与驱动器实际位移响应误差增大。因此,后续的研究工作应考虑提高驱动器制备工艺,同时结合漂移特性与迟滞特性补偿的综合逆控制模型,并将其扩展至中高频输入信号。
[1]Baughman R.Conducting polymer Artificial Muscles[J].Synthetic Metals,1996,78(3):339-353.
[2]Kim K J,Tan X,Choi H R,et al.Biomimetic Robotic Artificial Muscles[M].World Scientific,2013.
[3]Carpi F,Smela E.Biomedical Applications of Electroactive Polymer Actuators[J].Wiley and Sons,2009.
[4]Shahinpoor M,Kim K J.Ionic Polymermetal Composites:IV.Industrial and Medical Applications[J].Smart Materials and Structures,2005,14(1):197.
[5]李光,郑俊褒,傅均.采用聚吡咯修饰的QCM型三甲胺气体传感器[J].传感技术学报,2008,21(5):715-718.
[6]傅均,李光,邢建国.聚苯胺/TiO2修饰的QCM气敏传感器及湿度影响研究[J].传感技术学报,2011,24(4):475-479.
[7]Smela E.Conjugated Polymer Actuators for Biomedical Applications[J].Advanced Materials,2003,15(6):481-494
[8]李红星,李红星,朱文娜.基于模糊调整的神经网络逆模型控制[J].电气自动化,2005(4):24-26.
[9]刘怀民,王湘江.三层结构导电聚合物驱动器动态特性及其建模研究[J].机电工程,2015(6):783-787.
[10]Widrow B,Bilello M.Adaptive Inverse Control[C]//Proceedings of the Intelligent Control,1993:1-21.
[11]谢红卫,孙志强,宫二玲,等.现代控制系统[M].北京:电子工业出版社,2013:410-412.
[12]Levy E C.Complex Curve Fitting[J].IRE Transaction on Automatic Control,1959,4(3):37-41.
[13]Nguyen C H,Alici G,Wallace G G.Modelling Trilayer Conjugated Polymer Actuators for Their Sensorless Position Control[J].Sensors and Actuators A:Physical,2012,185:82-91.
[14]AliciG,HuynhNN.PerformanceQuantificationofConductingPolymer Actuators for Real Applications:A Microgripping System[J].IEEE/ASMETransactionsonMechatronics,2007,12(1):73-84.
[15]Croft D,Shed G,Devasia S.Creep,Hysteresis,and Vibration Compensation for Piezoactuators:Atomic Force Microscopy Application[J].Journal of Dynamic Systems,Measurement,and Control,2001,123(1):35.

刘怀民(1989-),男,硕士,现就读于南华大学,机械工程专业,研究方向为机电系统控制及自动化,lhmin0413@ foxmail.com;

王湘江(1972-),男,博士,教授,硕士研究生导师,主要研究方向为智能机构与技术、机电一体化技术、机电系统非线性控制理论与运用,wangxiangjiang72@ 163.com。
Inverse Model Control of Bending Conducting Polymer Actuators*
LIU Huaimin,WANG Xiangjiang*,SHANG Xingliang
(School of Mechanical Engineering,University of South China,Hengyang Hu’nan 421001,China)
An inverse model control method without external sensors is presented for conducting polymer actuators.It is accurate that transfer function of actuators system established through a system identification approach and an inverse control system which is based on four-order transfer function actuator system is simple in structure,and easy to be realized.It adopts drift compensation to improve precision control on conducting polymer actuators.The experiment result shows that the proposed inverse model with drift compensation is effective and accurate for actuator displacement tracking and tracking error meets control requirements.
biosensor;conducted polymer actuators;system identification;inverse model control
TH165
A
1004-1699(2016)10-1522-07
项目来源:湖南省教育厅重点项目(13A081);湖南省研究生科研创新项目(CX2015B401)
2016-03-17修改日期:2016-04-12

