基于HHT的脑电信号在不同阅读模式下的识别与分类*

梅婉欣，徐　莹，柯大观

（1.杭州电子科技大学生仪学院生物医学工程研究所，杭州310018；2.温州医科大学生物医学工程系，浙江温州325035）

基于HHT的脑电信号在不同阅读模式下的识别与分类*

梅婉欣1，2，徐莹1，柯大观2*

（1.杭州电子科技大学生仪学院生物医学工程研究所，杭州310018；2.温州医科大学生物医学工程系，浙江温州325035）

目的：针对Powerlab脑电信号记录仪获取脑电波形，分辨不同类型的脑电阅读模式。方法：对实验者在阅读不同材料（平静闭目、阅读英语、阅读诗歌、阅读现代文四种阅读模式）时的头皮脑电信号进行采样，使用希尔伯特-黄变换及支持向量机训练，分辨平静闭目和其他三种不同阅读模式，并针对经验模态分解时出现的常见情况——端点飞翼现象进行算法优化处理并比较其处理效果。结果：基于多项式拟合处理的经验模态分解分解后的脑电信号辨识率最高，稳定在65%水平，最高可达70%。结论：大脑在阅读状态下经经验模态分解和多项式拟合后的信号适合作为大脑阅读模式下的特征提取函数，并对有效阅读模式具有指导意义。

脑电信号分析；希尔伯特-黄变换；端点效应；经验模态分解；支持向量机

EEACC：11814；11819；11820doi：10.3969/j.issn.1004-1699.2016.10.001

脑电信号中包含了大量的大脑活动、生理疾病等信息，其采集方式主要分为有创和无创两种方式。脑电信号是一种非线性时变的不稳定信号，其分析方法从最初的傅里叶变换、到小波变换等，均为了更好适应脑电波形的特点，以提取最佳的脑电特征波形。传统的傅里叶变换方法使用简单，但只能表现信号的总体趋势，实效性不好；小波变换可适应信号的各种频率变化，但和傅里叶变换一样都受到Heisenberg测不准原理制约；而希尔伯特-黄变换HHT（Hilbert-Huang Transform）［1］可以不受该制约，且具有自适应性，在时间和频率上能够同时达到最高的精度，兼顾时间分辨率和频率分辨率，能够将信号分解为频率不同的各阶IMF函数，实际应用过程中可根据需要选择性地使用，因而可适用于分析非线性非稳定生物医学信号，如脑电信号等［2-3］。HHT能够将非线性非平稳信号的不明显特征提取出来，这一特点使得HHT很快在各领域取得良好的应用效果，并且其理论基础也在不断改进，近几年基于HHT及相关的阈值去噪技术在脑电信号提取中获得了较好的应用［4-6］。国内研究较为集中在对HHT的改进之上，并使用一些仿真实验比较其改进效果。钟佑明［7］提出使用分段幂函数法对信号进行包络计算，从而削弱了频率突变对包络模型产生的影响；张郁山［8］将HHT应用于地震分析中，使用Hilbert地震谱分析地震的时动性；胡欢［9］等使用HHT变换对经传感器采集得到的数字信号进行IMF函数的选择性滤除，可以有效改善传感器的线性度。黄锷所在团队也在不断丰富对HHT的理论，2006年提出了不同于三次样条插值的“b样条方法”作为一种计算信号包络模型［10］；2011年提出了多维的总体经验模态分解方法，由最初的若干阶IMF函数到多维的发展，更好地呈现出信号的特征［11］；2010年提出“平滑经验模态分解”，在一定程度上提高了IMF的分解精度，减轻了分解出的IMF常常存在模态混叠的现象［12］。但作为一种通用算法，存在一些不同类别具体信号的适用性问题。因此，本文着重对HHT中的EMD分解和分解后得到的IMF各阶函数的获取作了部分优化及改进，以期获得大脑在阅读模式下的最佳特征波形及特征提取，从而达到对各种不同类型阅读模式的脑电信号进行分辨的目的。

1　方法

HHT主要分成经验模态分解EMD（Empirical Mode Decomposition）和希尔伯特（Hilbert）谱分析两个过程，EMD分解是通过三次样条插值将原始序列分解为若干个本征模态函数 IMF（Intrinsic Mode Function），Hilbert谱分析则是将分解得到的IMF函数分量进行希尔伯特变换（Hilbert变换）得到Hilbert能谱图。首先，对于Hilbert谱分析的过程，主要是将EMD分解得到的IMF函数做Hilbert变换：设某阶IMF函数为ci（t）（表示i阶IMF），得其复解析信号为：

其中ai（t），φ（t）分别为函数

则忽略剩余函数rn（t），可得：

该公式即表示Hilbert能量谱。但是单纯谱分析方法建立在信号是平稳随机过程的假设之上，而脑电信号并不满足平稳性的假设，因此谱分析方法在分析脑电信号的应用中具有不可避免的局限性。所以本文侧重于从时域上对脑电信号进行EMD分解，基于信号的局部特征时间尺度，把复杂的信号分解为有限的内在模式函数之和，则每一个本征模态函数IMF所包含的频率成分不仅与采样频率有关，最重要的是随信号本身的变化而变化，然后针对IMF函数的使用方法进行了IMF函数分量的组合与部分使用条件的改进。该方法非常适用于研究非平稳的生物医学信号，如脑电信号，于本文第3节详述。

2　实验

2.1实验目的及过程

本实验旨在分辨大脑不同的阅读模式。为了使实验结果有更好的对比性，将脑电信号的获取分别在安静闭目模式下与阅读英语、阅读诗歌和阅读现代文三种阅读模式进行比较，分别区分安静闭目模式和其他几种阅读模式下脑电信号的特征量变化。

实验在安静室内操作进行，使用多通路工作电极及参考电极记录脑电信号：电极分别为置于前额的前额工作电极和置于头皮后部的枕部参考电极，另外为了减少干扰源需要贴一接地电极。实验中对实验对象的大脑分别在不同阅读模式（安静闭目、阅读英语、阅读诗歌、阅读现代文四种模式）下的脑电信号进行采集。每次待脑电呈现周期性稳态时候开始采集，经一系列实验参数设置及调整最终将脑电信号保存为adichet格式文件输出。

2.3数据采集

本实验使用的是 Powerlab多导电生理仪（ADInstruments公司，澳大利亚）。该系统是一种计算机数据采集系统，包括软件和硬件部分，它采用不同种类信号采集线分别将人体心电、脑电、肌电等传输进计算机，通过LabChart软件对参数进调节，对采集的信号进行基本采样。

Powerlab脑电信号采集部分采用电极帽进行，属无创的、对人体无损的采集方式。实验设备采集的是正常人体在不同阅读模式（安静闭目类型、读现代文类型、读英语类型、读诗歌类型）下的脑电信号。其中系统参数设置：采样率为400/s，量程为2 mV，低通滤波50 Hz（EEG模式），高通滤波0.5 Hz（EEG模式）。采集10个被试者在四种阅读模式下的脑电信号各30组，共300组，每组时长1.5 min。选取其中表现较为稳定，波形较为稳定的200组作为每种阅读模式下的实验数据。为保证实验结果的特征量可比性，不同被试者的实验数据进行归一化处理，再进行同一阅读模式下的多组采集及归类分析。实验过程及仪器接口等如图1所示。

图1　测试过程及仪器接口

3　经典HHT存在的问题

对实验获取的脑电信号经过EMD分解得到的各阶IMF函数分析，发现图像中会存在两端曲线飘飞、不稳定的发散现象，也叫“端点飞翼”现象。并且随着EMD分解的进行，端点飞翼现象往往会越来越严重，进一步“污染”到内部数据。这种现象在使用EMD原始分解方式时都会存在。如图2为安静闭目模式下的信号和其经过EMD分解的各阶IMF函数，其中图2（a）是原始信号的时域函数，图2（b）是它的频谱图，图2（c）、2（d）、2（e）、2（f）分别为IMF1、IMF2、IMF3和IMF4。

图2　原始阅读模式下的信号和经过EMD分解的各阶IMF函数

由图2（a）、2（b）可以看见安静闭目模式下的脑电信号频谱集中在某几个特定的频段，EMD分解可以将不同频段的函数分离出来得到各阶不同频率的IMF函数。并且由图2（c）、2（d）、2（e）、2（f）各阶IMF函数的分解得到的顺序可以看出，越早分离出来的IMF函数，其频率越大；另一方面，也可看出该模式下的脑电信号经EMD分解在第二个IMF就出现了端点效应，且端点效应在之后分解中开始向内部扩散。该现象会导致IMF两端数据无效；越迟分离出来的IMF函数，两端无效数据越长，甚至完全无效。产生该现象的原因往往是在使用三次样条插值对信号进行包络时，会出现上下两个包络交叉的现象，导致得到的平均值意义不大；并且当信号两端本身就是极大值或极小值时更易出现端点飞翼现象。针对这种现象，解决方法有多种：对于长信号，可不断截取产生端点飞翼现象的两端数据；对于短信号，可以对数据进行端点延拓；改进包络模型，使其可在保留信号长度的基础上，达到减轻甚至消除信号端点飞翼现象的目的。针对该过程的具体处理，蔡艳平［13］提出最大Lyapunov指数边界延拓方法，利用Lyapunov指数的几何特性，建立Lyapunov指数预测模型；DENG Y J［14］提出使用神经网络延拓技术对信号进行延拓；Faltermeier R［15］提出使用滑动窗口法对两端数据进行延拓；本文则使用多项式拟合方式对包络模型进行改进，从而达到减少端点效应的目的。

4　HHR算法改进与结果分析

对于HHT算法中的EMD分解这种信号处理方式来说，其过程涉及到噪声的滤除、包络模型的使用和最终IMF函数的使用方式［16］。由于本文主要针对的是最终IMF函数的选择及组合来作出改进，所以首先需要完成EMD的分解（图3），主要步骤如下：

①设输入的脑电信号为s（t），且令

②找出脑电信号rn-1（t）中所有极大值和极小值，将所有的极大值（极小值）通过三次样条插值获得上（下）包络线；分别记为uk-1（t）和vk-1（t）；

③将上包络线和下包络线的均值mk（t）作为新的序列。

④由原数列减去该新的序列，

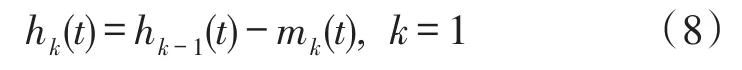
⑤得到的序列如果符合IMF函数，则其为一阶IMF，若不是，则重复步骤①～步骤④，相应参数n+ 1，直到符合条件得到一阶IMF。

⑥参数k加一且重复步骤①～步骤④得到一阶、二阶、……、n阶IMF函数。

图3　脑电信号的EMD分解过程

EMD分解过程不是无止境的，分解是否停止由以下函数确定：

可以设定SDk小于某个值时EMD分解结束，具体根据实验需要设置。

由以上过程可以看出，EMD分解具有完整性：

本文对于EMD方法的改进主要是根据所获取的脑电数据，试验得出最佳 IMF阶数、最佳IMF组合、最适合IMF长度以及对EMD分解过程中产生的端点效应进行了处理，以期得到最佳处理方式。

4.1最佳IMF阶数

一组脑电信号数据经EMD分解后最终会得到若干阶IMF，每阶IMF含有基本脑电信号的某些特征，而哪一阶能够真正包含有不同种脑电类型的特征值区别则需要经过实验适用性证明。本文采用不同阶的IMF函数，根据支持向量机最终结果，获取其中最佳IMF作为代表脑电特征的波形。实验使用的是脑电闭目模式与其他三种模式之间的对比分辨，长度均为2 000点的信号，然后将所有结果统计如图4所示，其中图4是对阅读英语和安静闭目两种模式的识别率分析。经过实验结果的对比，使用脑电信号在第4、5次分解出的IMF作为特征信号相对于直接使用原始信号进行支持向量机分类的识别率高出10%，并且阅读诗歌和安静闭目、阅读现代文和安静闭目两组的模式识别结果也表现出与图4一致的结果，说明第5次分解出的IMF（即IMF5）最适合作为阅读模式下的脑电特征波形分析。

图4　不同阶数的IMF所得识别率（阅读英语和安静闭目模式的区分）

4.2最佳IMF组合

若仅用脑电信号的某阶IMF作为脑电信号的特征波形，实验结果还并不理想。不同阶的IMF可能包含该种脑电信号区别于其他信号的特征，从而需要两种或以上的脑电信号同时作为区别于其他信号的特征波形。由于分离出越早的IMF函数其频率成份越高，说明相邻的IMF函数最可能包含相同的特征信息，所以实验通过相邻IMF阶数两两组合、或三三组合的方式得到最佳IMF组合，若经试验IMF组合以后的效果比不组合后的识别效果更好，证明该IMF组合更能作为代表该种脑电信号的特征波形。实验取的是长度为2 000点的信号，在同种情况下分别实验闭目模式与其他三种模式的辨别，将实验数据统计分析，如图5所示，将安静闭目与阅读英语两种模式进行识别统计。统计结果表明，以IMF3+IMF4+IMF5组合和IMF3+IMF4得到的识别概率最高，分别为65%和64%。在实际处理过程中，IMF3+IMF4+IMF5处理时间比IMF4+IMF3的时间多了300 s，所以在实验如果使用大样本数据（大于3 000点时）进行辨别时IMF3+IMF4更适合，可以大大缩短处理时间并达到较好的辨别率；如果样本量少（2 000点甚至更少时），使用IMF3+IMF4+IMF5组合更佳。

图5　不同IMF组合所得识别率

4.3最适信号处理长度

由于最初的脑电信号采集得到的脑电数据较为冗长，导致处理时间较长，并且得到的处理效果不一定最佳。所以实验通过改变采样数据长度，试图得到最适合的数据长度，从而减少实验时间，将更多时间用于改进其处理方法，提高机器识别不同种类的脑电波形的能力。如表1所示，是对IMF3的脑电信号进行识别，可以发现，当数据长度在500点时，处理时间较短，但识别率极低（30%左右），且不稳定；当数据长度在3 000点及以上时，识别率相对比较稳定，但处理时间大大增长，当数据量低于1 000点时，由于1 000的长度在端点效应处理时的稳定效果不佳，故不采用1 000的长度作为最佳IMF长度；由表1可看出，在数据长度为大约2 000点时，可兼顾时间与识别率，因此实验中将其作为最佳处理长度。

表1　不同信号长度记录表

4.4端点效应的解决

端点效应是EMD分解过程中普遍存在的一种现象，也是影响后期分解出的IMF效果好坏的一个重要因素。有多种方法可以用于减少端点现象的出现，本文通过信号长度的优化及多项式拟合等方法，主要改进及实践了其中的2种方法。

4.4.1处理后信号长度的截取

端点效应，即为信号两端的存在失真，最简便的改变这种现象的方法是不断抛弃这些失真的部分，剩下的就是分解有效的数据，进而对这些有效的数据进行分析处理。对于长数据来说，使用该种方法不但可以减少计算机处理的数据量，提高运算速率，还可以避免端点无效部分对整个分析过程的影响。所以本文根据计算机原本分析出的最佳IMF阶数，对该阶数IMF函数进行比较，分析其出现端点效应的数据长度，对该数据截取后再对不同的脑电数据进行处理。如图6所示，阅读英语和阅读诗歌两种模式在经过对端点数据的截取后，信号识别率均有所提升。

图6　经端点数据截取后信号识别率比较

4.4.2多项式拟合

多项式拟合也是针对端点效应的一种有效拟合方式。端点效应表现为两端曲线不受预测地向高幅度或低幅度偏离发散，导致两端数据失真甚至无效。而多项式拟合的意义在于将多项式函数不断逼近一个函数，这对于原本突然发生发散的函数而言，可以通过调整多项式拟合的各参数，达到削弱函数发散的程度。

本文的多项式拟合是基于最小二乘法的曲线拟合方式，按照偏差平方和最小的原则来确定拟合曲线，将曲线的拟合图像整体控制在最贴近原始数据的状态之下。该方式能够使得进行包络算法时的脑电信号两端平滑，并且通过调整拟合时的各个参数，得到最佳拟合曲线。例如，同样的信号数据，经多项式拟合后，由于降低了原本极易出现的端点飞翼程度，减少了由于端点问题导致的识别误差，使得经过处理后的信号在进行识别时表现出较好的稳定性。实验发现，经多项式拟合后的信号分解所得到的IMF函数在作为识别对象时，相对未经拟合的函数，具有更高的识别效果。其识别率稳定在65%，最高时可达到70%，相较于未改进的方法而言（最高识别率60%左右），具有一定的优化处理效果。

5　结果与讨论

本文通过改进型的HHT检测出最佳的区别不同种类脑电特征的方法，其主要作用是用于不同阅读模式下的脑电信号识别。因此该实验的主要评价标准是脑电信号处理时间和不同种类脑电信号识别概率。脑电信号作为一种医学信号，表现的是人的某种或几种生理或心理状态，已经或正在被用于医学研究和临床实验，如何让处理脑电信号的时间更短、甚至具有实时处理效果，将大大方便该研究的推广和临床的应用。另一方面，对不同种类脑电识别概率越高，证明该种脑电信号区别于其他脑电信号的特征提取实现得越好。所以兼顾识别速率和识别效果，处理时间和识别概率是作为本文特征识别情况的评价标准。

如图7所示，最终结果得出经过多项式拟合等优化算法改进后的EMD分解脑电信号，达到的识别率最强，稳定在65%，最高时可以达到70%。相对于最原始的信号，辨别率提高了15%；相对于经典EMD分解使用的IMF函数，虽然针对不同阅读模式的识别率提高有所区别，但识别率总体也呈现一种上升趋势；同时，就最高识别率而言，经多项式拟合的EMD分解效果并不显著；但经多项式拟合的信号呈现出更强的稳定性，更具有统计意义。

图7　不同阅读模式下的处理方式比较

6　总结与展望

本文主要介绍了目前HHT的应用领域；分析了HHT本身存在的问题；使用HHT对脑电信号进行处理，采用各阶IMF函数辨别不同阅读模式下的脑电信号；根据信号适应性问题，在HHT方法的过程中对EMD分解量进行改进，通过对支持向量机识别率和Matlab处理数据时间的综合考量得出了最优处理方式。进一步的实验需要完善以下一些内容：首先，需要对信号的去噪和电极的前处理进行优化；其次是进一步增大数据的采集量，从而在统计测试上具有更大的实验意义。

综上，本文通过基于HHT原型变换，分析得出经过多项式处理的EMD分解得到的IMF4+IMF5最适合作为大脑不同阅读模式下脑电信号的特征波形，稳定在65%水平，这对于脑电信号的研究提供了一种较好的研究方法和应用前景。另外，实验结果发现，大脑在阅读诗歌状态下的脑电活动程度接近于安静闭目模式，呈“准休息态”；而在阅读英语时，相对于阅读诗歌和阅读现代文，呈明显的“工作态”，这对于大脑健康与脑电活动的针对性分析具有一定的参考价值。在当今物联网发达并且终端传感等设备广泛普及的情况下，大脑对视觉接受到的海量信息进行高速处理消化，如何科学阅读，如何选择及组合不同阅读及工作模式，提高阅读效率、避免大脑长期“亚健康”状态，对进行脑电-有效决策阅读模式研究具有重要意义。相较于阅读模式，大脑在潜意识状态下产生的脑电波形以及主动意识下进行的思考（如运动想象、逻辑分析等）是截然不同的。非线性非稳态生物医学信号处理方法的改进，对大脑在主动思考时的脑电模式研究、以及在该模式下脑-机接口的发展都有巨大推动作用，而在现实生活中也已有了相关成品的出现——如基于HHT快速分析手段的脑—机械手［17］的研究发展等。并且随着HHT等脑电信息分析技术的广泛应用，人们对大脑皮层各个区域功能，尤其是左脑理性思维与右脑想象思维的联系与整合认识的提高，对大脑思维模式有效阅读训练参数的快速采集与分析，将大大推动人脑接受海量数据和有效阅读的潜力，这也将推动对各种可穿戴设备（如眼球追踪、意念操控、视觉记忆、虚拟现实方向等）的研究和市场化［18-19］。

［1］Huang N E，Shen Z，Long S R，et al.The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-Stationary Time Series Analysis［J］.The Royal Society，1998，454（1971）：904-995.

［2］张雪梅.基于HHT的非平稳信号特征提取与参数估计方法研究［D］.电子科技大学，2015.

［3］Daubechies I.The Wavelet Transform，Time Frequency Localization and Signal Analysis［J］.IEEE Tansactions on Information Theory，1990，65（5）：961-1006.

［4］Yeh J R，Sun，Shieh J S，et al.Intrinsic Mode Analysis of Human Heartbeat Time Series［J］.Annals of Biomedical Engineering，2010，38（4）：1337-1344.

［5］马玉良，许明珍，佘青山，等.基于自适应阈值的脑电信号去噪方法［J］.传感技术学报，2014，27（10）：1368-1372.

［6］Lin C F，Su J Y，Wang H M，et al.Hilbert-Huang Transformation Based Analyses of FP1，FP2，and Fz Alectroencephalogram Signals inAlcoholism［J］.JournalofMedicalSystems，2015，39（9）：275-281.

［7］钟佑明，金涛，秦树人.希尔伯特-黄变换中的一种新包络线算法［J］.数据采集与处理，2005（1）：13-17.

［8］张郁山.希尔伯特—黄变换（HHT）与地震动时程的希尔伯特谱［D］.中国地震局地球物理研究所，2003.

［9］胡欢，余永，王慧，等.HHT算法在压电陶瓷驱动器的微纳米位移传感器中的应用（英文）［J］.传感技术学报，2014，27（4）：456-462.

［10］Chen Q，Huang N E，Riemenschneider S，et al.A B-Spline Approach for Empirical Mode Decomposition［J］.Advances in Computational Mathematics，2006，24（1-4）：171-195.

［11］Zhao H W，Huang N E，Chen X Y.The Multi-Dimensional Ensemble Empirical Mode Decomposition Method［J］.Advances in Adaptive Data Analysis，2011，1（3）：339-372.

［12］Pao S，Young C，Tseng C，et al.Smoothing Empirical Mode Decomposition：A Patch to Improve the Decomposed Accuracy［J］.Advances in Adaptive Data Analysis，2010，2（4）：521-543.

［13］蔡艳平，李艾华，张玮，等.HHT端点效应的最大Lyapunov指数边界延拓方法［J］.仪器仪表学报，2011（6）：1330-1336.

［14］Deng Y，Wang W，Qian C，et al.Boundary-Processing-Technique in EMD Method and Hilbert Transform［J］.Chinese Science Bulletin，2001，46（11）：954-960.

［15］Faltermeier R，Zeiler A，Keck I R，et al.Sliding Empirical Mode Decomposition［C］//Neural Networks（IJCNN），The 2010 International Joint Conference on IEEE，2010：1-8.

［16］陈一贤.HHT方法分析［D］.浙江大学，2007.

［17］杨林豹.基于α波的脑机接口研究及在智能轮椅上的应用［D］.北京：北京工业大学，2011.

［18］Banerjee A，Sanyal S，Patranabis A，et al.Study on Brain Dynamics by Non Linear Analysis of Music Induced EEG Signals［J］.Physica A：Statistical Mechanics and its Applications，2016，444：110-120.

［19］Hsu W Y.Brain-Computer Interface Connected to Telemedicine and Telecommunication in Virtual Reality Applications［J］.Telematics and Informatics，2016.

梅婉欣（1992-），女，杭州电子科技大学在读研究生。研究生期间致力于人体生理电信号的处理工作，尤其是脑电信号的噪声处理与特征提取，1358986643@ qq.com；

徐莹（1978-），女，浙江大学生物医学工程博士，副教授，硕士生导师。学术任职/社会任职为杭州电子科技大学生仪学院测试计量及仪器系系副主任。主要研究方向为从事科研方向主要包括多种传感器微芯片仿真、设计及总体硬件平台搭建、后期信号分析工作，xuying@hdu.edu.cn。

Recognition and Classification of EEG Signal in Reading Mode Based on Hilbert-Huang Transformation*

MEI Wanxin1，2，XU Ying1，KE Daguan2*
（1.Hangzhou Dianzi University Biomedical Engineering Institute，Hanzhou 310018，China；2.Department of Biomedical Engineering，Wenzhou Medical University，Wenzhou Zhejiang 325035，China）

Objective To distinguish different kinds of EEG signals from the high-dimensional and redundant mass EEG nonlinear-data by Powerlab.Methods Firstly，EEG signals were sampled from an experimenter’s scalp when the experimenter was reading different kinds of books（closing eyes，reading English books，reading poems and reading modern Chinese）.Secondly，HHT transform（Hilbert-Huang Transform，HHT）and Support Vector Machine method were used to train and distinguish the model of closing eyes and other three kinds of reading patterns.Finally，the algorithm is optimized because of its frequent phenomenon-end issue that occurred during the Empirical Mode Decomposition and the results were analyzed.Results the Empirical Mode Decomposition based on polynomial fitting algorithm could be used to recognize largest amount of EEG signals by 70%.Conclusions The experimental results demonstrate that the Optimized HHT algorithm based on Empirical Mode Decomposition and polynomial fitting algorithm can effectively make use of the information from the mass EEG nonlinear-data signal and is suitable and practical method of classification for research.

EEG signal analysis；hilbert-huang transform；end issue；empirical mode decomposition；support vector machine

TP212.3

A

1004-1699（2016）10-1471-07

项目来源：国家自然科学基金项目（30800248，31300939）；浙江省公益技术研究社会发展项目（2016C33G2041024）；浙江省自然科学基金项目（LY13C100003）

2016-03-21修改日期：2016-05-10