基于球形内检测器的管道内磁场测量*
陈冠任,李 健,黄新敬,陈世利,徐天舒
(天津大学精密测试技术及仪器国家重点实验室,天津300072)
基于球形内检测器的管道内磁场测量*
陈冠任,李健*,黄新敬,陈世利,徐天舒
(天津大学精密测试技术及仪器国家重点实验室,天津300072)
球形管道内检测器在管道安全检测领域具有十分广阔的应用前景,但其在滚动过程中测得的磁场信号呈周期性,无法直观反映管道内磁场分布情况,给识别焊缝和计算管道走向带来了一定的困难。针对此问题本文推导了滚动坐标系下球形内检测器测得的磁场与管道内平动坐标系下磁场之间的数学关系,并利用处于同一滚动坐标系下的加速度信号构建了转换模型,然后设计实验和算法验证了模型的正确性。实验结果表明,平动磁场的计算值和实测值在数值大小和变化趋势上均吻合良好,误差绝对值的平均值基本不超过1 μT。
管道;球形内检测器;磁场;测量
EEACC:7230doi:10.3969/j.issn.1004-1699.2016.10.004
长输管道作为国民经济的生命线,是油气能源生产和供应链中不可或缺的桥梁,是工业生产的重要支柱。管道一旦发生泄漏,将会造成不可估量的经济损失和严重生态环境污染[1-2]。目前,一些比较成熟的管道泄漏检测手段包括负压波法、光纤法等[3]能够实现对管道实时在线监测和对泄漏的准确定位,但它们只适用于检测泄漏量较大的突发性泄漏,对微小泄漏并不敏感;内检测法[4]虽然能够检测微小泄漏和缺陷,但管道内检测器PIG(Pipeline Inspection Gauge)对管道变形十分敏感,存在较高的卡堵风险,因而限制了其应用。
球形管道内检测器[5-6]是一种新型的管道内检测工具。这种内检测器在管道中油品的推动下滚动前进,沿途记录管道内泄漏声信号、磁场信号以及自身加速度信号等多种信息,待检测结束后由上位机离线分析处理,识别泄漏并对其定位。该球形内检测器一方面具有传统漏磁内检测器经济快捷、能够检测微小泄漏的优点;同时,因为其直径小于管道内径,所以对管道变形并不敏感,通过性良好,非常适合管道微小泄漏检测。针对这种球形管道内检测器(下称内检测器),科研人员设计了一套多传感器数据采集与存储系统[7]应对各种工况下的球体机械结构[8],并对其在管道竖直管段的通过性和影响因素进行了仿真研究和实验验证[9-10]。
对于一些因为地势险要或埋地较深而无法使用地面标记装置AGM(Above Ground Marker)[11-13]进行定位的管线,利用内检测器对管道内磁场进行研究在辅助定位、焊缝识别以及管道走向计算等方面具有十分重要的意义。Kobayashi等人基于等效磁荷法[14]对圆柱体的均匀轴向磁化问题做了大量研究,并取得了许多成果[15-17]。黄新敬采用等效磁荷法研究了管道内磁场的分布情况[18],还分别对无缝钢管与螺旋钢管焊缝处的磁场分布进行了分析,并提出了利用管道内磁场识别和定位焊缝的方法[19,20];赵伟分析并建立了管道的磁屏蔽模型[21],得到了地磁场经管道屏蔽后的管道内剩余磁场与管道走向之间的数学关系,并基于该模型提出了一种管道走向的计算方法[22]。
以上提到的利用管道内磁场进行焊缝识别和管道走向计算的方法中,所使用磁场均为球形内检测器测得的滚动坐标下的磁场信号。该信号呈旋转周期性,无法直观反映管道内磁场的情况,因而在识别焊缝时需要使用小波对磁场信号进行处理提取焊缝处的磁场突变,而且随着管道内磁场强度的改变使用的小波函数和层数也不相同,信号处理和参数选择比较复杂;而计算管道走向时则要求内检测器在管道内行进过程中时刻围绕磁传感器的一个敏感轴转动,以获得在管道轴向上的磁场分量大小,条件过于苛刻。因此,如果能够直观地得到沿线各点的管道内磁场的大小与方向,不仅能够简化焊缝识别算法,还可以提高管道走向计算的精度和方法的适用性。针对此问题,本文推导了滚动坐标下内检测器测得的磁场(下称滚动磁场)和管道内平动坐标系下的磁场(下称管道平动磁场)之间的数学关系,并利用同处滚动坐标下的加速度信号建立了相应的数学模型来计算管道平动磁场,最后设计了地磁场实验对模型进行了验证。
1 建立模型
本课题组经多次现场实验发现:通过对球体转动惯量的特殊设计,在较短的一段时间里,内检测器能够保持围绕一个固定的方向轴滚动[6,14];对比内检测器在管道中运动速度和油品流速,发现二者基本一致,而后者相对稳定,因此内检测器在短时间内能够保持速度匀速。基于以上两点,推导模型如下。
内检测器中磁传感器所在滚动坐标系Os-XsYsZs(简称为传感器滚动坐标系)与“东-北-天”大地平动坐标系Oe-XeYeZe的关系如图1(a)所示。内检测器围绕转轴Ye以角速度ω沿Xe轴正向滚动。将Os-XsYsZs的原点Os移动至Oe使二者重合,如图1(b)。分别计算Os-XsYsZs各轴在Oe-XeYeZe各轴上的投影,可以得到滚动磁场Bs各分量与大地平动磁场Be各分量之间的关系如方程(1)所示。各个方程中的系数是Xs、Ys、Zs分别与Xe、Ye、Ze的夹角的余弦值。

图1 大地平动坐标系与传感器滚动坐标系(一)
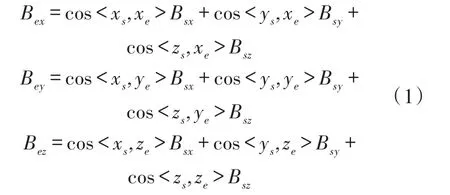
式中,xs、ys、zs分别是沿Xs、Ys、Zs正向的单位向量。xe、ye、ze分别是沿Xe、Ye、Ze正向的单位向量。

图2 大地平动坐标系与传感器滚动坐标系(二)
如图2所示,设Xs、Ys、Zs与Ye的夹角分别为θx、θy、θz,同时以角速度ω绕Ye旋转,并扫过一个以自身为母线、以自身和Ye夹角的二倍为顶角的无限大圆锥面。现以Xs为例,设其上一点M在Ye上的投影为l,旋转半径为r,向量OM分别与Xe、Ye、Ze的夹角余弦值如式(2)~式(4)。其中xm、ym、zm分别是OM在Os-XsYsZs各轴上分量。

因为xm、ym、zm和xs、ys、zs方向相同,所以二者与xe、ye、ze的夹角余弦值也相同。参考式(2)~式(4)可以推导得到Ys、Zs与Xe、Ye、Ze的夹角余弦值。带入新系数值将式(1)重写为:
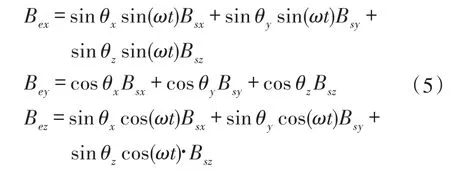
由于加速度传感器和磁传感器的敏感轴方向完全一致,而且其一直处于恒定的重力场中,因此可以使用加速度信号来确定式(5)的系数。但是测得的加速度信号中除了包含我们需要的重力加速度分量(交流),还存在由内检测器滚动造成的向心加速度分量(直流),因此必须先去除加速度信号中的直流分量与噪声。除去直流分量和噪声后的加速度信号中的重力加速度分量在Xs方向上的分量表达式如下:

同理可得其Ys、Zs方向上的分量的表达式:
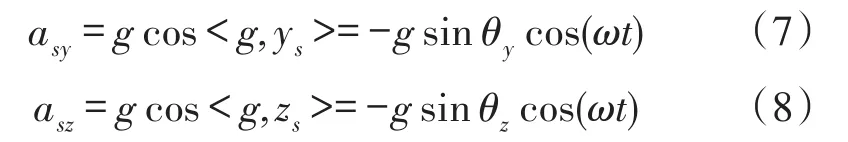
根据式(6)~式(8)可以直接得到式(5)中Bez关于Bsx、Bsy、Bsz的系数。同时易知Bex与Bez相位差为π/2,因此可通过移相得到Bex的系数。经观察Bex、Bey、Bez关于Bsx、Bsy、Bsz对应系数的平方和为1,因此可以求得Bey的系数大小。
Bey系数的正负取决于传感器在内检测器中安装的位置、转轴的方向以及滚动的方向。而内检测器在管道实际运行中,不同时段的转轴方向和管道方向都有可能发生变化,系数的正负也会随之变化,因而通常只采用平动磁场的Bex和Bez分量计算管道走向。本实验中滚动方向、转轴方向均为已知,故可确定其系数的符号。
当管道与地平面呈一定角度时,管道平动磁场Bp需要经过转换得到。如图3所示,当管道与地面夹角为α,同时其在地面上的投影与正东方向所成角度为φ,管道坐标系与大地坐标系之间的转换可以通过式(9)实现。其中Bpx、Bpy、Bpz为Bp在管道Op-XpYpZp坐标系下的三轴磁场分量。

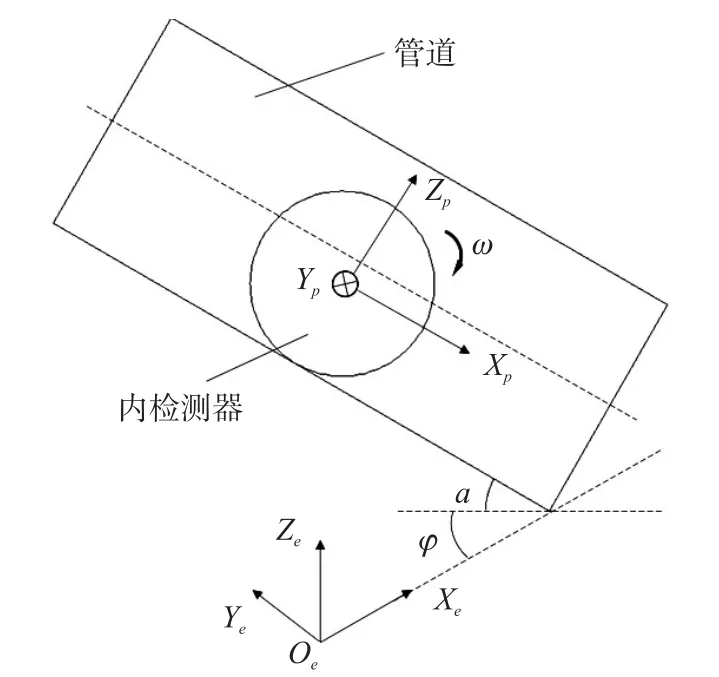
图3 大地坐标系与管道坐标系
2 实验
由于管道的屏蔽作用,管道内磁场强度相比于地磁场强度要弱一些,但考虑到二者大小均为数十微特,属同一数量级,因此可通过测量地磁场对模型进行验证。实验选择了一处地磁场相对均匀的开阔地,使用内检测器和作为参考的高精度磁阻式三轴微型数字磁场计HMR2300[23,24]分别对不同走向的一段6 m长路径上的地磁场进行了测量,如图4(a)所示。图4中X、Y、Z轴分别对应管道坐标系Op-XpYpZp中的Xp、Yp、Zp轴,但由于实验只对“管道”所在路径上的地磁场进行了测量,故下文将管道平动磁场简称为平动磁场。

图4 地磁场实验
为了能够更好地模拟管道中内检测器的运动情况,实验人员预先在地面上铺设了塑料地垫来模拟管道内的液体阻尼环境,减小其滚动过程中的振动。内检测器被固定在一个铝制套筒内以确保其定轴转动。同时,为探究模型对磁场异变的敏感程度,实验设置了对照组。如图4(b)所示,其中一组无铁磁体干扰,另一组放入了一段约0.5 m长的实验管道作为铁磁干扰,以探究模型对磁异常的敏感程度。
3 结果与讨论
算法流程如图5所示。

图5 算法流程图
虽然实验在一定程度上保证了内检测器围绕固定转轴这个条件,但由于不存在管道内油品的推力且套筒与地垫间存在摩擦力,内检测器在实际滚动过程中会减速,因而无法保证匀速运动。对此,可将测得加速度信号和磁信号等比例线性拉伸/压缩。
加速度传感器对滚动中的振动比较敏感,而且包含一些随机噪声,应使用零相位滤波器ZPSF(zero-phase-shift filter)[25]和中值滤波器(median filter,MF)[26]消除信号的毛刺与奇异点,对磁信号使用这两种滤波器亦可提高信号的光滑程度。之所以选用零相位滤波器和中值滤波器,是因为磁信号和加速度信号各分量之间存在着严格的相位关系,而这两种滤波器均能很好地保留信号各分量之间的初始相位。但需要谨慎选择滤波器参数,避免因参数选择不当造成信号失真。然后提取滤波后的加速度信号的重力加速度分量(交流),并做相应的归一化处理。同样,滤波后的磁信号也需要进行系数校正,以确保各轴信号的放大倍数一致。最后将计算得到的平动磁场再次进行零相位滤波以消除小幅波动,最终得到平动磁场的趋势。然而零相位滤波器的使用必然会在信号两端造成畸变,虽然可以通过优化算法在一定程度上减小畸变[27],但为了保证结果的正确性和真实性,应当将首尾处信号舍去,只保留中间一段作为研究对象。
东西向无铁磁干扰的实验结果如图7所示。可以看出,直接观察内检测器测得滚动磁场并不能得到太多的有用信息,而通过模型计算得到的平动磁场与HMR2300实测的平动磁场在数值和趋势上均十分相近。两条曲线不完全重合的原因包括:①内检测器中的磁传感器和加速度传感器不在正球心,计算得到的平动磁场实际为一条摆线上的平动磁场,因而内检测器和HMR2300的运动路径不完全重合;②内检测器中的磁传感器和HMR2300之间存在差异,另外传感器自身噪声和外界干扰也会对测量结果造成影响;③信号处理过程中引入的误差,比如滤波器参数选择不合适造成的信号失真。
东西向带铁磁干扰的实验结果如图8所示。观察图6和图7中的滚动磁场,发现二者除了因两次滚动时的初始姿态不同导致的相位上有所差异,并不能直观看出铁磁干扰的存在和影响。而对比两图的平动磁场测量值可以发现:虽然HMR2300的各轴磁场的输出值存在0.5~1 μT的漂移,但在其运动路径的2.5 m~3 m处(铁磁管道放置处)仍存在明显的磁场异变,而计算得到的平动磁场和实测磁场在异变处也吻合良好。

图6 等比例线性拉伸/压缩
改变内检测器滚动时的转轴方向与路径走向后再进行实验,计算得到的平动磁场值与实测值的误差如表1所示。其中γ为内检测器滚动转轴与Zs的夹角,为最大误差的绝对值,为误差绝对值的平均值,单位是μT。可见,除个别异常值以外,各轴最大误差的绝对值基本在2 μT以内,而误差绝对值的平均值基本不超过1 μT。“东北-90°”组之所以各轴的误差都比较大,是因为加速度传感器Y轴输出信号过小而输出噪声相对较大使得信噪比很低,导致用来计算平动磁场的模型系数误差较大,从而使得和均比较大。“东北-0°”组中加速度Z轴输出信号同样很小,但由于传感器自身特性差异,Z轴噪声相对Y轴更小些,因而对平动磁场计算结果影响较小。
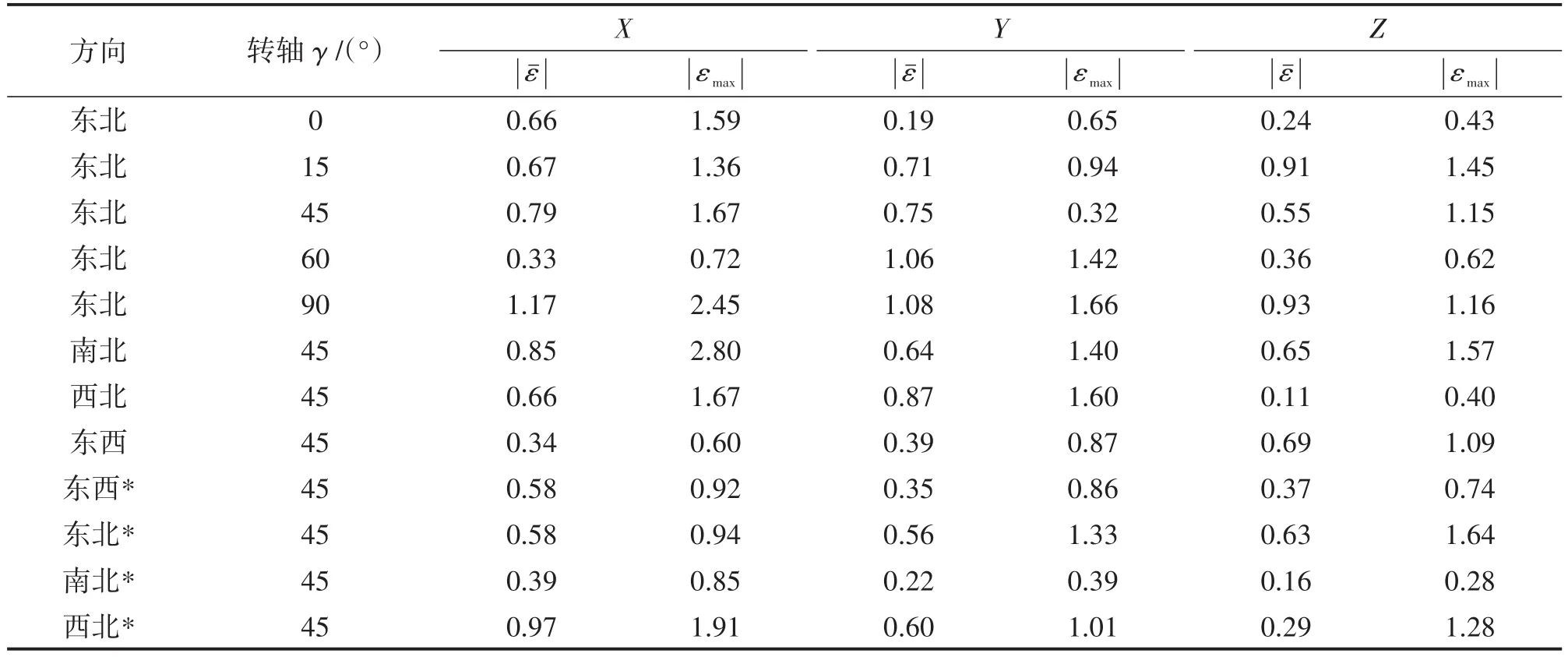
表1 改变走向与转轴后的误差表

图7 无铁磁干扰时东西方向滚动磁场以及平动磁场的计算值和实测值
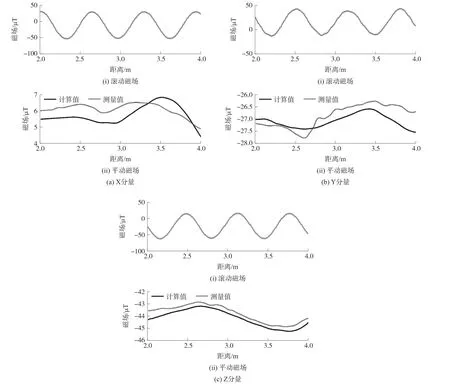
图8 引入铁磁干扰时东西方向滚动磁场以及平动磁场的计算值和实测值
4 总结与展望
本文提出和推导了内检测器测得的磁场和管道内平动坐标系下的磁场之间的数学关系,利用同处滚动坐标系的加速度信号建立了数学模型,设计了相应的信号处理算法,并通过地磁场实验验证了模型的正确性和实用性。实验结果表明:计算得到的平动磁场能够显著地反映实际磁场的大小与变化趋势,但由于实验操作、装配、传感器自身特性以及信号处理参数选择等一些因素的影响,计算值与实测值曲线不完全重合。当引入铁干扰之后,平动磁场计算值对铁磁管道造成的磁场异变依然敏感。最后,改变内检测器滚动转轴以及路径走向同样能够得到较小的实验误差。
为进一步提高现场实验时模型的适用性,可以针对文中出现的问题采取相应的措施,例如:①改进设计内检测器球体的机械结构:本模型要求内检测器在管道内定轴转动,虽然实验证明在很短的时间(数秒)里其确实能够保持定轴转动,但仍可进一步改进其机械结构,使其滚动更加平稳且更易于保持定轴转动②选择信噪比、分辨率和采样率更高的传感器:一方面是因为管道的磁屏蔽使得实际磁场较小,需要更高分辨率和信噪比的传感器;另一方面则是因为现场实验时内检测器中会安装电磁发射机,其发射的23Hz低频信号会影响磁场的测量结果,为将其滤除需要更高的采样率。
[1]Tonga Shujiao,Wub Zongzhi,Wanga Rujun,et al.Fire Risk Study of Long-Distance Oil and Gas Pipeline Based on QRA[J].Procedia Engineering,2016,135:368-374.
[2]Verde C,Molina L,Torres L.Parameterized Transient Model of a Pipeline for Multiple Leaks Location[J].Journal of Loss Prevention in the Process Industries,2014,29(1):177-185.
[3]Boaz L,Kaijage S,Sinde R.An Overview of Pipeline Leak Detection and Location Systems[C]//Pan African International Conference on Information Science,Computing and Telecommunications,2014:133-137.
[4]Gloria N B S,Areiza M C L,Miranda I V J,et al.Development of a Magnetic Sensor for Detection and Sizing of Internal Pipeline Corrosion Defects[J].Ndt&E International,2009,42(8):669-677.
[5]Fletcher R,Chandrasekaran M,Fletcher R,et al.Smart BallTM:A New Approach in Pipeline Leak Detection[C]//International Pipeline Conference,2008:117-133.
[6]郭世旭,陈世利,黄新敬,等.海底管道微泄漏检测器研制与应用[J].现代化工,2015(9):182-186.
[7]王正锋,陈世利,郭世旭,等.管道微小泄漏检测数据采集系统的设计[J].压电与声光,2014(4):564-568.
[8]崔尧尧,陈世利,赵吉波,等.海底管道微小泄漏球形内检测器结构设计[J].石油工程建设,2014,40(3):36-39.
[9]陈世利,高春倩,郭世旭,等.球形内检测器在海底立管内通过性仿真研究[J].计算机工程与应用,2015(19):265-270.
[10]陈世利,赵吉波,郭世旭,等.球形泄漏内检测器在海底管道竖直管段的通过性[J].纳米技术与精密工程,2015(1):1-7.
[11]刘梦然,张国军,简泽明,等.管道内检测器声定位技术研究[J].传感技术学报,2014(4):500-504.
[12]刘梦然,张国军,简泽明,等.一种用于管道地面标记的阵列式MEMS矢量声传感器仿真研究[J].传感技术学报,2014(2):184-189.
[13]Qi H,Zhang X,Chen H,et al.Tracing and Localization System for Pipeline Robot[J].Mechatronics,2009,19(1):76-84.
[14]Nakano S,Nomura T,Iwamoto M.Three-Dimensional Analysis of Leakage Field of Power Transformer[J].Electrical Engineering in Japan,1976,96(5):55-62.
[15]Kobayashi M,Ishikawa Y.Surface Magnetic Charge Distributions and Demagnetizing Factors of Circular Cylinders.IEEE Transactions on Magnetics,1992,28(3):1810-1814.
[16]Kobayashi M,Ishikawa Y,Kato S.Magnetizing Characteristics of Circular Cylinders in Perpendicularly Applied Magnetic Field.IEEE Transactions on Magnetics,1996,32(1):254-258.
[17]Ozaki K,Kobayashi M,Rowlands G.Surface Magnetic Charge Distribution of A Long,Thin Cylinder and Its Edge Singularity.IEEE Transactions on Magnetics,1998,34(4):2185-2191.
[18]Huang X,Chen S,Guo S,et al.Magnetic Charge mad Magnetic Field Distributions in Ferromagnetic Pipe[J].Applied Computational Electromagnetics Society Journal,2013,28(8):737-746.
[19]Huang X,Chen S,Guo S,et al.Analyses and Application of the Magnetic Field At Girth Welds in Pipelines[J].Measurement Science&Technology,2013,24(11):115007-115016(10).
[20]Zhang Y,Huang X,Chen S,et al.Analyses of Magnetic Field in Spiral Steel Pipe[J].Journal of Magnetism&Magnetic Materials,2015,375:210-216.
[21]赵伟,曾周末,陈世利,等.管道内地磁场特性分析及实验研究[J].仪器仪表学报,2012,33(7):1556-1560.
[22]Zhao W,Huang X,Chen S,et al.A Detection System for Pipeline Direction Based on Shielded Geomagnetic Field[J].International Journal of Pressure Vessels&Piping,2013,113(1):10-14.
[23]Ouyang J,Chen S,Zhang Y,et al.Measurement of the Anisotropy Fields for AMR Sensors[C]//Electron Devices and Solid-State Circuits(EDSSC),2011 International Conference of IEEE,2011:1-2.
[24]王立冬,孙世宇,王云峰.数字磁阻磁场仪在自行式武器导航中的应用[J].火力与指挥控制,2000,25(4):73-76.
[25]常广,鄢素云,王毅.零相位数字滤波器在非平稳信号处理中的应用[J].北京交通大学学报(自然科学版),2011,35(6):49-56.
[26]冯晅,刘财,杨宝俊,等.中值滤波器对信号相位和形状影响的研究[J].石油物探,2002,41(1):37-41.
[27]尚秀辉,郭爱煌,李广宇.基于零相位数字滤波器的边界问题的分析[J].电子测量技术,2010,33(4):25-27.

陈冠任(1992-),男,天津大学精密仪器与光电子工程学院硕士研究生,研究方向为输油管道内磁场检测,chenguanren@ tju.edu.cn;

李健(1973-),男,天津大学精密仪器与光电子工程学院教授,研究领域:管道安全检测、无损检测,tjupipe@tju.edu.cn。
In-Pipe Magnetic Field Measurement Using Spherical Inner Detector*
CHEN Guanren,LI Jian*,HUANG Xinjing,CHEN Shili,XU Tianshu
(State Key Laboratory of Precision Measurement Technology and Instrument,Tianjin University,Tianjin 300072,China)
Spherical inner detector has a board application prospect in pipeline safety detection.However,due to the detector’s rotation,the collected magnetic field signal is always periodic,which cannot reflect the actual condition of the in-pipe magnetic field directly and makes it difficult to calculate pipelines’orientation or discover the welds.A method is proposed to transfer the collected magnetic field signal in the rotating sensor frame to which in the stationary pipe frame.The relationship between them is deduced,and the mathematic model is built using the collected acceleration signal in the same rotating sensor frame as the acquired magnetic field signal.Experiment and algorithm are designed to verify the correctness of the model.The results show that the calculated magnetic field is in good agreement with the measured magnetic field both in value and trend,while the average of error’s absolute value is almost within 1 μT.
pipeline;spherical inner detector;magnetic field;measurement
TP393
A
1004-1699(2016)10-1486-07
项目来源:国家自然科学基金项目(61473205);天津市科技兴海项目(KJXH2013-06)
2016-04-25修改日期:2016-06-26
- 传感技术学报的其它文章
- 基于HHT的脑电信号在不同阅读模式下的识别与分类*
- Development and Test of Software Method to Achieve Constant-Temperature-Difference Control for Thermal Wind Sensor*
- Analysis of the Effect of the Equivalent Parallel Resistor of theComb Capacitive Accelerometer*
- 基于恒温谐波检测双回路瓦斯浓度仪研究*
- 炭黑/硅橡胶复合材料力敏元件热、力敏感试验研究*
- 一种基于霍尔效应的扭矩传感器*

