基于极坐标的扇束CT周期性优化算法

刘　辉，张　权，刘　祎，桂志国,2

(1.中北大学 电子测试技术重点实验室，山西 太原 030051；2.中北大学 仪器科学与动态测试教育部重点实验室，山西 太原 030051)



基于极坐标的扇束CT周期性优化算法

刘辉1，张权1，刘祎1，桂志国1,2

(1.中北大学 电子测试技术重点实验室，山西 太原 030051；2.中北大学 仪器科学与动态测试教育部重点实验室，山西 太原 030051)

为了提高传统扇束计算机断层扫描(Computed Tomography,CT)卷积反投影重建算法(Conventional Back-Projection,CBP )的重建速度，提出了一种快速的扇束CT重建算法.该算法结合极坐标特性，利用三角函数一定程度上的周期性，对传统CBP重建算法进行了改进，减少了正余弦函数的计算量和重建所需要的外围循环次数.同样利用该特性对极坐标重建后的图像坐标转换过程进行改善，从而对CBP算法进行了改进，降低了重建时间.

计算机断层扫描；卷积反投影；三角函数特性；极坐标

随着计算机断层成像技术(Computed Tomography，CT)的不断发展，CT重建技术越来越多地运用到医学诊断[1]、工业无损检测等行业中[2].CT重建主要有解析算法和迭代算法[3-5].与迭代算法相比，解析重建法以其重建速度快、重建图像质量高的特点，已经被广泛应用到工程上.CBP重建算法是解析算法中最具代表性的重建算法之一[6-8].虽然CBP重建算法重建所需数据量较少，但是运算数据量依然很大，还需要进一步提高其重建速度，才能更好地运用到工业上.

加权、卷积滤波和反投影是CBP算法的3个主要部分，其中反投影过程就占据了98.36%的重建时间[9]，因此反投影重建过程的改进是主要研究方向.文献[10]运用极坐标特性，提出了极坐标反投影重建算法(Polar Coordinates Back-Projection,PCBP)，但极坐标向笛卡尔坐标的转换过程中要使用插值运算，重建速度提高有限；文献[11]利用正余弦函数特性，将16幅投影同时进行反投影重建，提出了对极坐标重建的优化算法(Optimize Polar Conventional Back-Projection OPCBP)，该算法将重建速度提高了4倍；文献[12]利用了三角函数的对称性，提出了极坐标反投影对称优化算法(Symmetry Polar Conventional Back-Projection SPCBP)，同时对64幅预处理后的数据进行重建，将重建速度提高8倍.

本文利用三角函数一定程度上的周期性和极坐标反投影重建的特点，将144幅反投影数据同时进行反投影重建，使外围循环减少至传统算法的1/144，同时大大减少了三角函数的运算量，从而实现对传统算法的优化.本文称之为极坐标反投影周期性优化算法(Periodicity Polar-coordinate Conventional Back-Projection，PPCBP).

1　扇束CBP重建原理

扇束CT扫描示意图如图1所示，图中a(r,θ)是待重建图像切片的射线衰减系数分布函数；β为射线源投射角度；函数p(β,s)是该角度下的投影数据；D为射线源到物体重建中心的距离，重建公式为

(1)

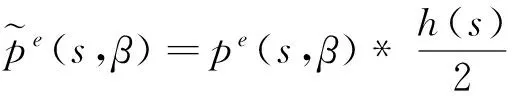
(2)

(3)

(4)

(5)

由式(1)～式(5)可知计算机实现CBP反投影重建时，首先通过式(3)给投影数据进行加权；其次通过式(2)对加权过的数据进行卷积滤波；最后根据式(4)和式(5)确定的射线的反投影地址s和加权因子U对滤波后的数据进行累加反投影重建.假设重建的图像的大小为N×N，投影角度为[0°,360°),投影视图数为M，该算法的反投影过程流程如图2所示，从图2中可以看出CBP反投影重建中运最复杂的就是对反投影地址s和加权因子U求解.由式(4)和式(5)可知，每次求s和U需要9次乘法(含除法)和6次正余弦函数运算，反投影过程总共需要次乘法和次正余弦运算，因此主要考虑对s和U求解过程的简化.

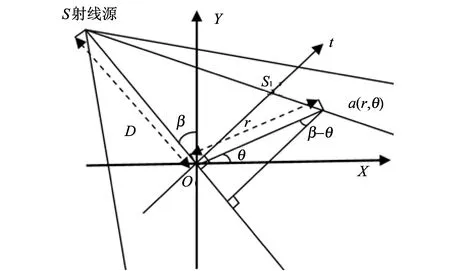
图1　扇束扫描示意图Fig.1　The scanning schematic of fan-beam

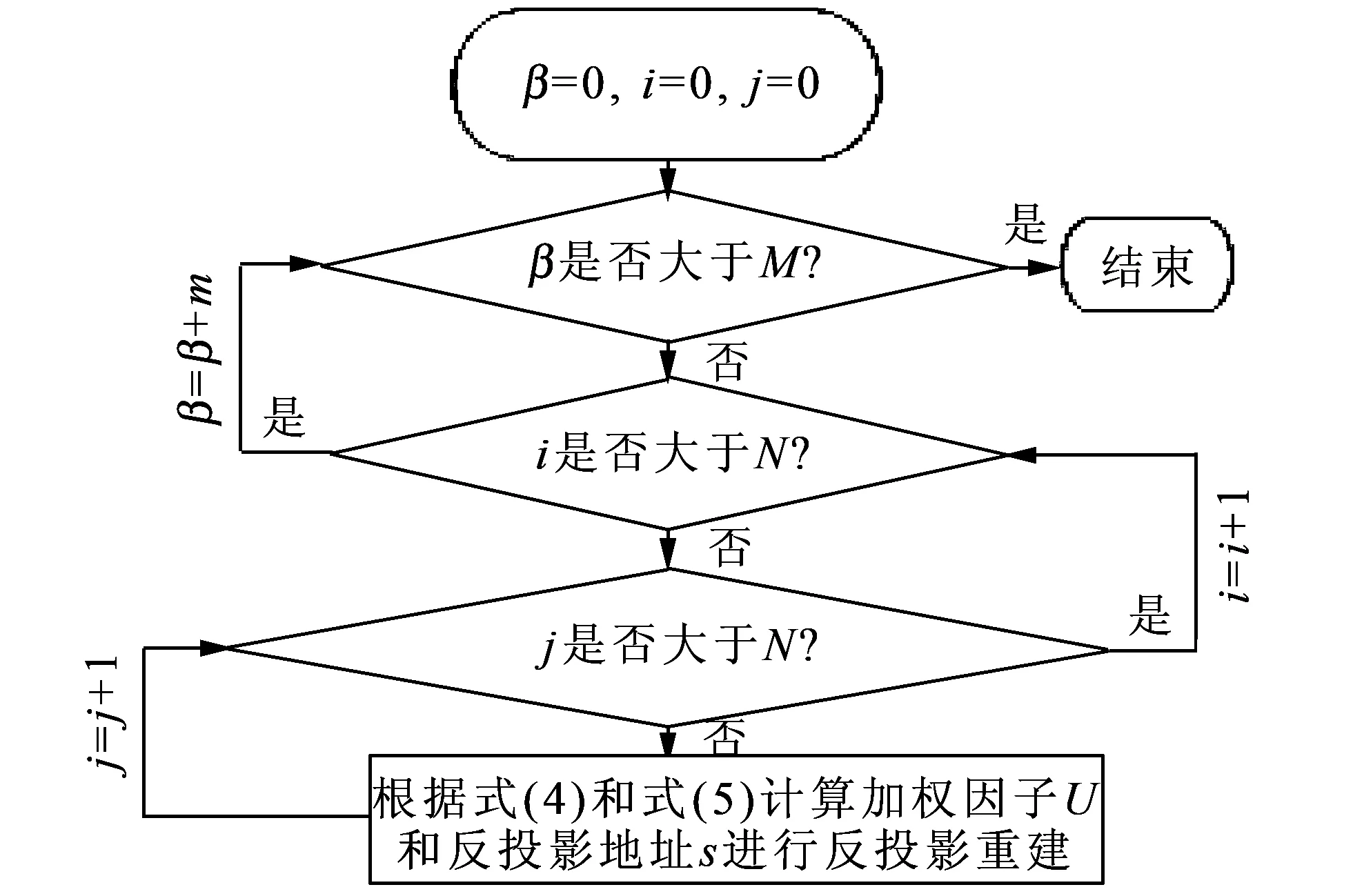
图2　CBP反投影重建过程流程图Fig.2　The flowchart of CBP back-projection reconstruction

2　极坐标下进行重建

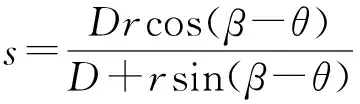
(6)

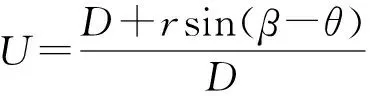
(7)

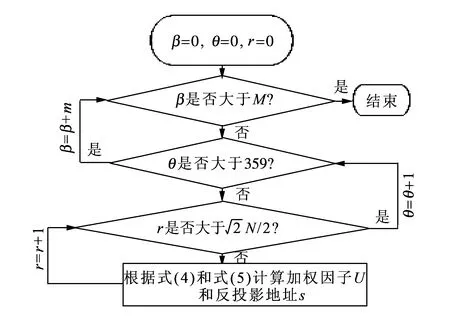
图3　PCBP反投影重建流程图Fig.3　The flowchart of PCBP algorithm

3　三角函数周期性优化

3.1反投影过程的优化

三角函数中30°，45°，60°和90°是几个特殊的角度，三角函数值很容易计算得出.通过简单的三角函数的诱导公式，可以得出120°,135°,150°,180°,210°,225°,240°,270°,300°,315°和330°的三角函数值，这些角度中除了45°及其诱导产生的角度之外，其余角度都是呈现出的等差关系，这些角度的正余弦值一定程度上表现出了周期性，给PCBP算法优化提供了很好的条件.分别让β-θ=30m(0≤m≤11,m∈Z)，讨论其正余弦值并研究各角度下的余弦值之间的关系

(8)

(9)

(10)

(11)

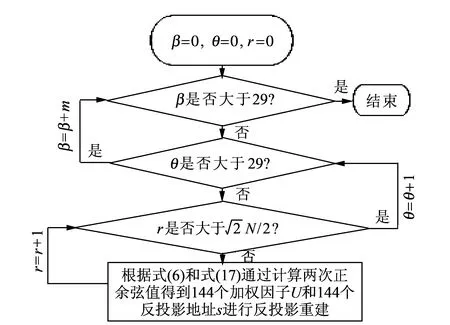
图4　PPCBP反投影重建流程图Fig.4　The flowchart of PPCBP algorithm

式(8)～式(10)之间关系只是差了一个正负号，而且A,B和A1,B1以及A2,B2具有式(12)所示的关系，因此只要求解出[0°,30°)范围内的正余弦值就可以求得所有扫描角度下β-θ的正余弦值，极坐标三角函数周期性优化算法(PPCBP)算法的反投影过程流程如图4所示.

(12)

通过以上分析，在一个投影角度β下通过三角函数的变换，只需要计算两次正余弦值就可以计算出θ+30m(0≤m≤11,m∈z)下的s和U的值，因此一个循环可以完成12个投影视角下的144个投影数据参与重建，外层循环减少为极坐标下的1/144，同时将三角函数计算量降低为极坐标下的1/72，大大提高了重建速度.所以PPCBP算法无论在循环，乘法或者是三角函数运算上都得到了很大的提高，在理论上证实了PPCBP的优越性.

3.2重建图像坐标转换的优化

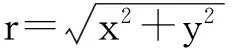
本文在图像的转换过程中采用双线性插值方法，如图5所示，双线性插值通过临近目标点G的A,B,C和D 4点经过3次线性插值从而求得G点像素值的过程，其原理如式(13)所示，其中P(x)代表了x点的像素值，a=BE/AB,b=DF/CD，c=FG/EF.

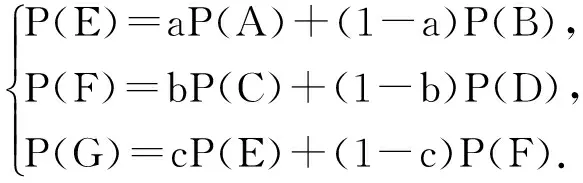
(13)

针对采用双线性插值增加的计算量，本文使用正切函数对称性对其简化.图6中所标记的点在极坐标中具有相同的值，且其正切值之间具有正负和互为倒数的关系.因此，如果知道极坐标下任意一个点的坐标，就能同时知道极坐标下其他7个点的坐标转换，使外围循环减少至改变前的1/8，同时使正余切函数值的计算量也减少至改变前的1/8，提高了坐标转换的速度.

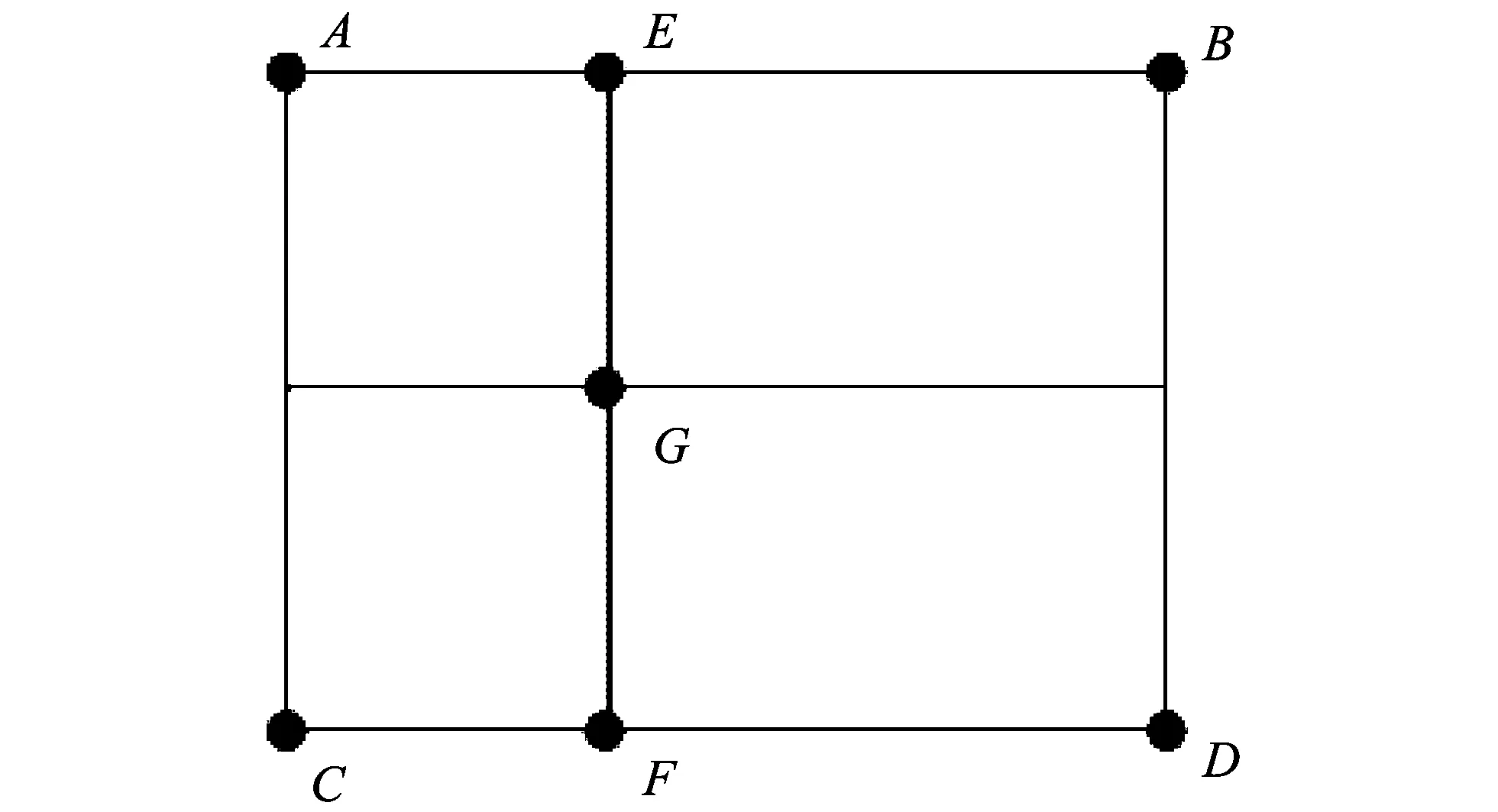
图5　双线性插值示意图Fig.5　The schematic of bilinear interpolation

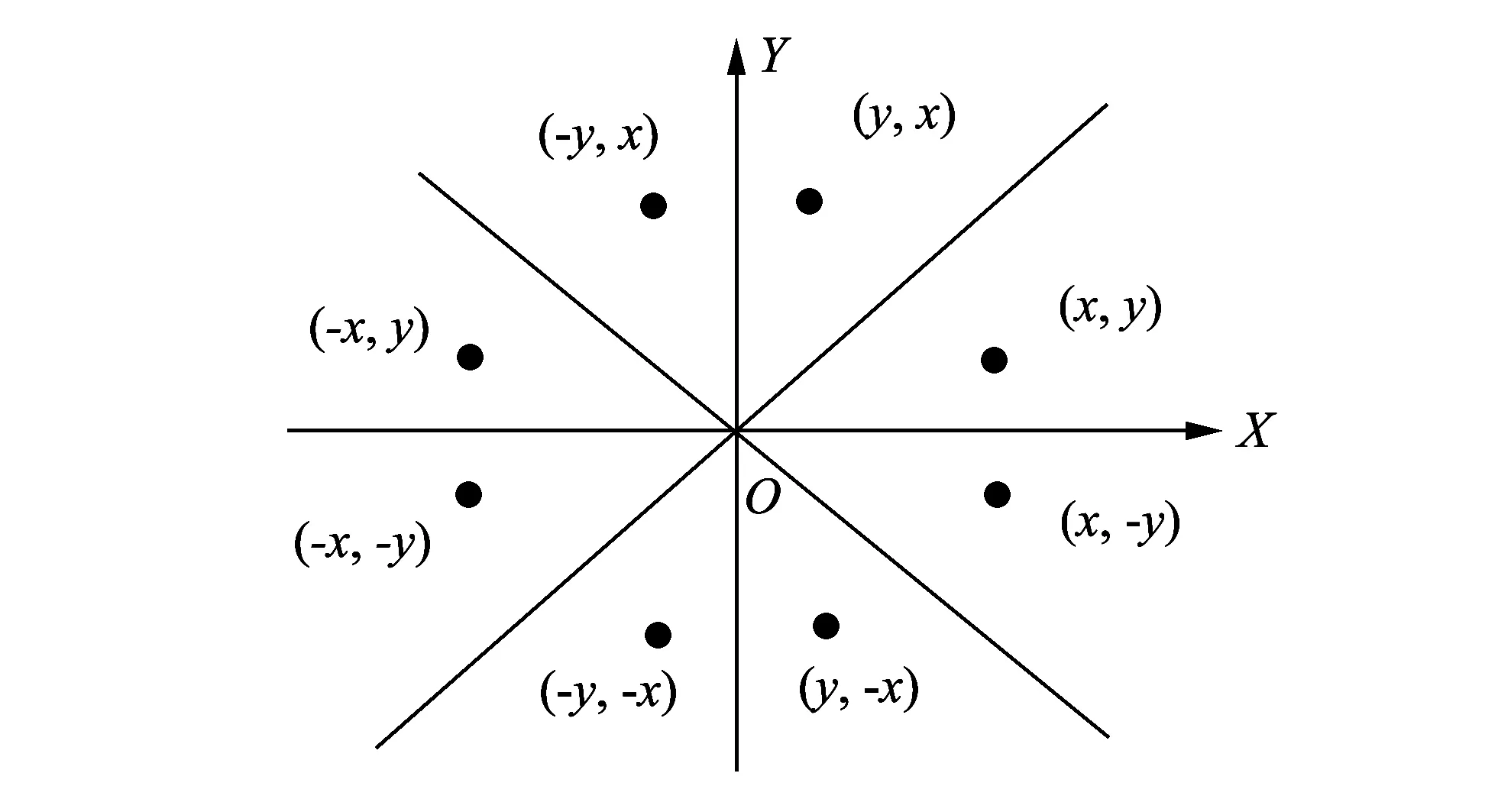
图6　坐标转换中像素点的选取示意图Fig.6　Pixels chosen schematic during coordinate transformation

4　实验结果

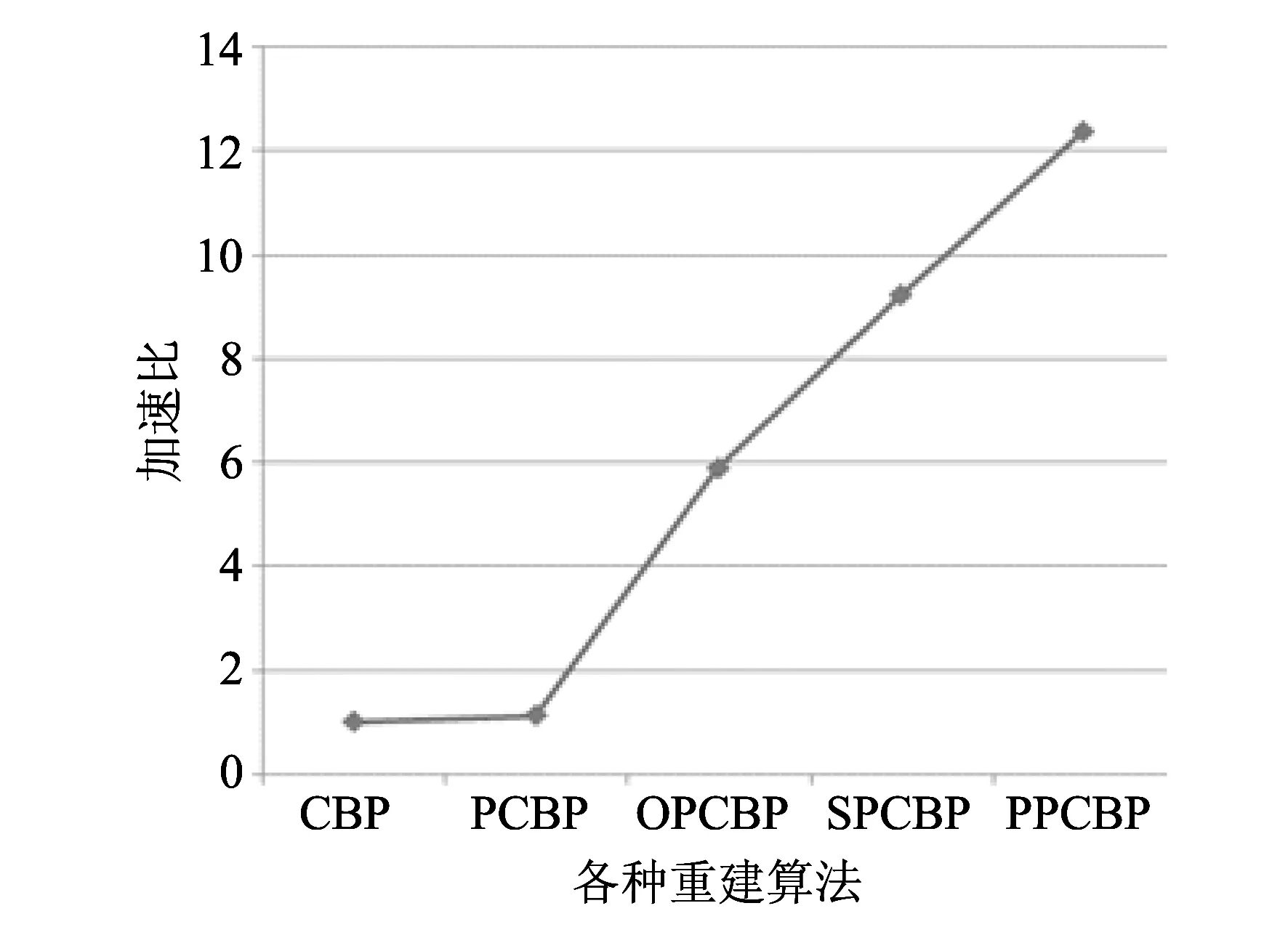
图7　各种算法相对CBP重建时间加速比Fig.7　The speedup time compared with CBP

为了验证本文算法的可行性，将PTCBP算法和CBP算法、PCBP算法、OPCBP算法和SPCBP算法的重建结果进行对比.实现本文算法的软件设备为Windows 7 32 b操作系统和VC++6.0编译环境；硬件设备为英特尔 Pentium(奔腾)双核 E5400@2.70 GHz处理器，DDR3 2G金士顿内存.投影数据参数如下：射线源到旋转中心的距离为800 mm，物体中心到探测器的距离为150 mm，射线为ISOVOLT 450，探测器为paxscan2520，探元大小0.127 mm，电压110 kV，电流2.5 mA，投影数据大小为570×460，投影视图数为360，重建图像大小为512×512.

4.1重建速度比较

各算法的重建时间如表1所示，加速比如图7所示：从重建的时间和加速比上可以看出，PTCBP算法的速度是CBP算法的将近12.5倍，是PCBP算法的近10倍，是SPCBP的近1.5倍，是OPCBP的2.1倍.因此，本文所提出的PPCBP算法大大提高了CBP算法的重建速度.由于使用的是三角函数一定程度上表现出来的周期性原理，使得重建过程中所占用的内存也大大减少，在计算机编程中充分展示了PPCBP算法的优越性.

表1　各算法重建速度对比表

4.2重建图像质量比较

各种算法图像如图8所示，从图中我们很难看出图像之间的差别，图9展示的是各算法重建出图像的第145列像素大小之间的对比，从中我们发现各图像之间差别很小，说明了利用PPCBP算法重建出的图像与其他重建算法重建出的图像在质量上没有明显的差别.为了量化本文算法重建出的图像与其他算法重建图像之间的差别，本文采用归一化均方距离 (Normalized Mean Square Distance,NMSD)和归一化平均绝对距离(Normal Average Absolute Distance,NAAD)对图像质量进行评估，其公式分别为

(14)

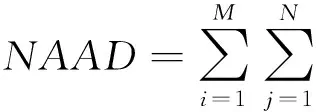
(15)

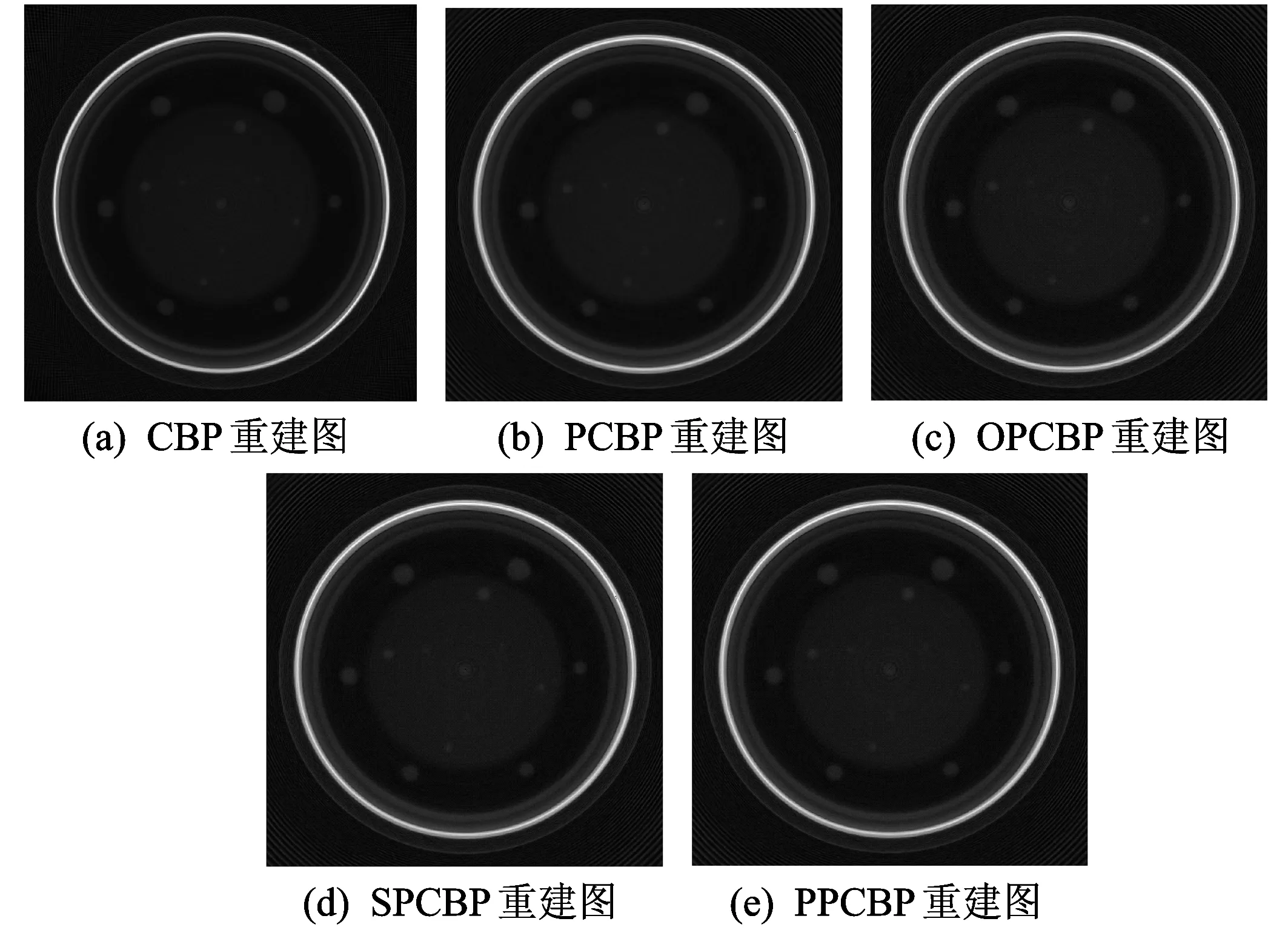
图8　各种算法重建图像质量对比图Fig.8　The quality comparison chart of the images constructed by different algorithms

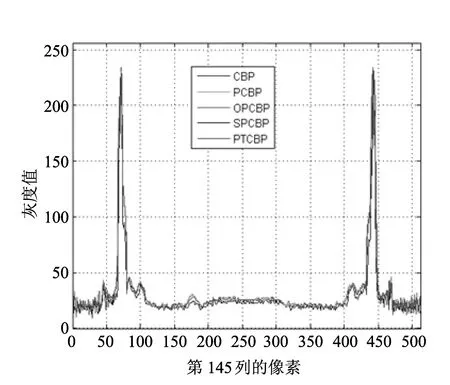
图9　各算法第145列像素大小对比图Fig.9　The comparison of pixels in the 145th row but from different images reconstructed by vary algorithms.

算法CBPPCBPPTCBPOPTCBPSPCBPNMSD-0.3881030.3881080.3881040.405673NAAD-0.1984530.1984590.1984540.217913

由表2可知，无论是从归一化均方距离还是归一化平均绝对距离上PTCBP算法跟PCBP,OPTCBP和SPCBP算法重建出的图像在质量上没有明显的差别，因此进一步的说明PTCBP算法在重建图像时并没有引入误差，PTCBP算法在保证图像质量上有良好的适用性.

5　结　论

本文提出的PTCBP算法结合三角函数一定程度上的周期性以及对称性分别对反投影过程和坐标转换过程进行了改进.在保证了重建图像质量的前提下，很大程度上提高了传统CBP算法的重建速度.

[1]曾更生.医学图像重建[M].北京：高等教育出版社,2010.

[2]Franco L,Tahoces P G,Martínez-Mera J A.Visualization software for CT：fan/cone beam and metrology applications [J].Procedia Engineering,2013,63(63)：779-785.

[3]庄天戈.CT原理与算法[M].上海：上海交通大学出版社，1992.

[4]Rit S,Oliva M V,Brousmiche S,et al.The Reconstruction Toolkit (RTK),an open-source cone-beam CT reconstruction toolkit based on the Insight Toolkit (ITK)[C].Journal of Physics：Conference Series.2014,489：012079.

[5]Wang A S,Stayman J W,Otake Y,et al.Soft-tissue imaging with C-arm cone-beam CT using statistical reconstruction[J].Physics in Medicine and Biology.2014,59(4)：1005.

[6]Zhang F,Du J,Jiang H,et al.Iterative geometric calibration in circular cone-beam computed tomography[J].Optik-International Journal for Light and Electron Optics,2014,125(11)：2509-2514.

[7]Zheng Fang,Xin Gu,Xing Liang Zhang,et al.Research on the relationship between projection number and image noise level in FBP reconstruction [J].Advanced Materials Research.2013,718-720：2324-2328.

[8]Xin Y,Yang J,Xie Z Q,et al.An overlapping semantic community detection algorithm base on the ARTs multiple sampling models[J].Expert Systems with Applications,2014,42(7)：3420-3432.

[9]刘晓平.扇束卷积反投影法的程序优化[J].CT 理论与应用研究.1996,5(1)：35-37.

Liu Xiaoping.Program optimization of swctor-beam convolution backprojection[J].Computerized Tomography Theory and Applications,1996,5(1)：35-37.(in Chinese)

[10]杨民,路宏年,黄朝志.用查找表和极坐标反投影法实现计算机断层扫描快速重建[J].兵工学报，2004,35(4)：476-479.

Yang Min,Lu Hongnian,Huang Chaozhi.Fast computed tomography reconstruction with look-up table and polar coordonate back-projection[J].Acta Armamentarii,2004,35(4)：476-479.(in Chinese)

[11]张銮，桂志国.扇束等距CT极坐标反投影重建算法的速度优化[J].无损检测，2010,32(2)：95-98.

Zhang Luan,Gui Zhiguo.Speed optimization of polar coordinate back-projection rectonstruction algorithm for fan beam collinear equispaced CT[J].Nondestructive Testing,2010,32(2)：95-98.(in Chinese)

[12]张晶，张权，刘祎，等.扇束CT极坐标反投影重建算法的对称优化[J].计算应用.2014,34(6)：1711-1714.

Zhang Jing,Zhang Quan,Liu Yi,et al.Symmetry optimization of polar coordinate back-projection reconstruction algorithm for fan beam CT[J].Journal of Computer Applications,2014,34(6)：1711-1714.(in Chinese)

Periodic Optimization Algorithm Based on Fan-Beam CT Polar Coordinates

LIU Hui1,ZHANG Quan1,LIU Yi1,GUI Zhiguo1,2

(1.State Key Laboratory of Electronic Measurement Technology (North University),Taiyuan 030051,China；2.Instrument Science & Dynamic Measurement,Ministry of Education Key laboratory of (North University),Taiyuan 030051,China.)

To improve the reconstruction speed of traditional fan-beam CT image reconstruction based on fan-beam conventional back projection (CBP),a fast polar coordinate back projection reconstruction algorithm was proposed.Combining with the features of polar coordinate,the proposed algorithm applied the trigonometric periodicity in some degree,and improved traditional CBP to reduce the amount of computation of trigonometric function and the times of external cycle in reconstruction process.Similarly,the mentioned properties were also used in the process of the conversion between polar coordinate and Cartesian coordinate to improve the CBP algorithm and the reconstruction time gets reduced.

computed tomography; conventional back-projection; trigonometric function characteristics; polar coordinate

1671-7449(2016)05-0394-06

2016-03-01

国家自然科学基金资助项目(61271357)；国家重大科学仪器设备开发专项资助项目(2014YQ240445)；山西省自然科学基金资助项目(2015011046)

刘辉(1989-)，男，硕士生，主要从事图像重建的研究.

TP391.4

Adoi：10.3969/j.issn.1671-7449.2016.05.005