基于投影寻踪的机械装备测试性分配方法研究

周　平，刘杰林，刘东风

(1.中国人民解放军92557部队，广东 广州 510720；2.海军工程大学 青岛油液检测分析中心，山东 青岛 266012)



基于投影寻踪的机械装备测试性分配方法研究

周平1，刘杰林1，刘东风2

(1.中国人民解放军92557部队，广东 广州 510720；2.海军工程大学 青岛油液检测分析中心，山东 青岛 266012)

借鉴可靠性分配模型建立方法，建立了机械装备测试性分配模型；并将测试性分配问题转化为求分配因子，提出了基于投影寻踪的子系统重要度评价方法，依据子系统重要度，获得各子系统分配因子并最终分配测试性指标；以柴油机为例进行了测试性分配，结果证实论文提出的分配方法合理可行.

机械装备测试性；指标分配；投影寻踪；分配因子

装备长期使用和维修实践表明，传统先研制出装备再考虑测试诊断问题的模式，已不适应装备发展形势，不仅保障能力形成滞后，保障工作盲目被动，无法实施精确保障，而且维修保障的总费用也无法承受.必须改变思路，从设计抓起，全系统全寿命周期地考虑装备测试诊断问题，才能使装备全寿命周期内性能最优而费用最省.测试性正是这样一门技术，通过在设计阶段就考虑与测试诊断有关因素，使装备能及时准确地确定其状态并隔离其内部故障.当前，对装备开展测试性设计已势在必行，而测试性设计过程中，首当其冲的是要做好测试性分配工作，只有在设计之初明确测试性指标要求，才能使测试性与其它技术指标一样得到考量，才有可能使装备获得良好的测试性.

测试性分配影响因素较多，主要包括故障影响程度、可靠性、维修性、监测难易度及经济性等.国内外学者针对电子装备测试性分配开展了较多研究，总体来看主要是通过评判系统各组成部分在测试性设计中的重要度而展开，相关研究成果促进了电子装备测试性水平的提高.但对机械装备而言，还未有明确的测试性指标要求，相应的测试性分配方法也未曾涉及[1,2].本文借鉴可靠性分配建模理论，对机械装备测试性分配模型进行研究，并就测试性分配过程中人为因素干扰过多的问题，引入投影寻踪对机械装备测试性指标实施分配，结果客观可信.

1　机械装备测试性分配模型

可靠性分配中由于子系统之间存在串并联关系而分配模型亦不一样，测试性分配中同样存在串并联的情况，但对机械装备可认为子系统之间是串联关系，系统测试性串联框图如图1所示，影响机械装备测试性分配的主要因素有各子系统故障影响程度G1、可靠性G2、维修性要求G3、监测难易度G4、经济性G5.

图1　机械装备测试性串联框图Fig.1　Block diagram of testability in series

1.1故障检测率分配模型

设某机械装备系统由n个分系统组成，这时，对于故障检测率，有

等价变换得

定义αiD为i第个分系统的分配因子，表示第i个分系统检测出的故障数占总检测出的故障数的比例

于是有

若事先求得αiD，γFDs改为γFDsa，则

(6)

式中：γFDsa为给定的系统级故障检测率.式(6)即为FDR的分配模型.

由于γFDi∈[0,1]，于是

即有

式中：βiD为该分系统的故障数占总检测出的故障数的比例.

于是，FDR的分配问题归结为求分配因子αiD.

1.2故障隔离率分配模型

由故障隔离率函数关系

等价变换得

定义αiI为第i个分系统FIR的分配因子，表示第i个分系统隔离出的故障数占总隔离故障数的比例

(10)

于是有

式中：γFIsa为给定的系统级故障隔离率. 式(13)即为FIR的分配模型.

(13)

式中：γFIsa为给定的系统级故障隔离率.式(13)即为FIR的分配模型.

由于γFDi∈[0,1]，于是

(14)

即有

式中：βiI为第i个分系统检测的故障数占总隔离故障数的比例.

于是，FIR的分配归结为求分配因子αiI.

1.3分配因子的生成

以故障检测率的分配因子αiD为例来说明分配因子的生成思路[3]：根据式(5)可知，在进行测试性分配时，必须保证各子系统所获得的故障检测率分配因子αiD相加之和等于1；又由式(7)可知，各分配因子理论上允许的最大值相加之和等于1/γFDsa，因此，可以以各分配因子允许的最大值βiD为基准，向下降低以获得各子系统故障检测率的分配因子，且满足所有子系统向下降低之和等于(1/γFDsa-1).由此，我们可以采取如下方法进行故障检测率分配因子的生成：按照装备测试性分配影响因素组成，求得各子系统在这些测试性分配影响因素下的重要度，显然，由这些影响因素进行评判的重要度大的子系统应获得较高的测试性指标，降额度应小一些；重要度小的子系统获得的测试性指标要低一些，降额度应大一些.因此，可采用如下公式计算各子系统分配因子向下的降额度

因此，可采用如下公式计算各子系统分配因子向下的降额度

同理，可得各子系统的故障隔离率分配因子αiI的计算公式为

需要指出的是， 按照上述方法计算分配因子时， 可能存在某个子系统最终得到的αkD（或αkI）小于0的情况， 这是由于该子系统基准值βkD（或βkI）较小， 且该子系统重要度又较小，导致分配因子的降额度εkD（或εkI）大于该子系统所允许的最大值βkD（或βkI）的缘故. 遇到此种情况时， 可以将该子系统的降额度εkD（或εkI）置为0，即不对该子系统进行降额处理， 而将总的降额度(1/γFDsa-1)(或(1/γFIsa-1))在其余子系统间进行分配，依此类推，确保各子系统最终得到的分配因子αkD（或αkI）都大于0.

2　基于投影寻踪的机械装备子系统重要度评价

由第1节确立的测试性分配模型，分配问题转化为求各子系统的重要度，因此，如何确定各子系统在测试性分配时的重要度成为关键，人为赋权固然简单省事，但决策者主观偏好将影响最终的评判结果，使评价结果可信度下降，为增强评判过程的客观性，本文引入投影寻踪对机械装备测试性指标进行分配，这种方法不需要人为赋权，评价结果更加客观可信.

2.1投影寻踪(PP)模型

PP是用来处理和分析高维数据，尤其是来自非正态总体的一类统计方法，既可作探索性分析，又可作确定性分析，其基本思路是：将高维数据通过某种组合投影到低维子空间上，并通过优化投影指标函数，寻找出能反映原高维数据结构或特征的投影向量，在低维空间上对数据结构进行分析，以达到研究和分析高维数据的目的.应用PP的目的是对机械装备各子系统综合重要度进行评价，即根据综合重要度大小对各子系统进行排序，可以利用投影寻踪分类模型，模型构建过程主要分为以下步骤[4]：

① 样本评价指标集的归一化处理.设各指标值的样本集为{x*(i,j)|i=1,2,…,n; j=1,2,…,p}，其中{x*(i,j)}为第i个样本第j个指标值，n和p分别为样本的个数(样本容量)和指标的数目.为消除各指标值的量纲和统一各指标值的变化范围，可采用下式进行极值归一化处理：

对于越大越优的指标

对于越小越优的指标

(20)

其中：xmax(j)和xmin(j)分别为第j个指标值的最大值和最小值，x(i,j)为指标特征值归一化的序列.

② 构造投影指标函数.PP方法就是把p维归一化数据{x(i,j)|j=1,2,…,p}综合成以a(a(1),a(2),…,a(p))(a是单位向量)为投影方向的一维投影值z(i)，

综合投影指标值时，要求投影值z(i)的散布特征应为：局部投影点内部尽可能密集，类间尽可能散开.基于此，投影指标函数可表达为

(22)

Sz为投影值z(i)的标准差，Dz为投影值z(i)的局部密度，即

(24)

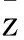
③ 优化投影指标函数.当各指标值的样本集给定时，投影指标函数Q(a)只随着投影方向a的变化而变化.不同的投影方向反映不同的数据结构特征，最佳投影方向就是最大可能暴露高维数据某类特征结构的投影方向.因此可通过求解投影指标函数最大化问题来估计最佳投影方向，即

(25)

(26)

这是一个以{a(j)|j=1,2,…,p}为优化变量的复杂非线性问题，用传统的优化方法处理较难，本文采用遗传算法来解决其高维全局寻优问题.

④ 分类(优序排列).把步骤(3)求得的最佳投影方向a*代入式(21)，可得各样本点的投影值z*(i).投影值z*(i)和z*(j)进行比较，二者越接近，表示样本i与j越倾向于分为同一类.按z*(i)值从大到小排序，则可将样本从优到劣排序.

2.2影响因素评分标准

根据机械装备测试性分配确定的影响因素，对各子系统开展测试性设计的各影响因素进行评分，评分标准如表1所示.采用10分制，满分10分，考虑评分时存在的模糊性，分数可以是0～10之间任意数，如故障影响程度为10分，表示故障的发生影响安全；如故障影响程度为9分，表示故障的发生对系统的影响介于“可能影响安全”和“影响安全”之间.

表1　影响因素评分标准

由表1确定的装备各子系统测试性分配影响因素评分标准，以典型机械装备柴油机为例对各子系统测试性设计时各影响因素进行评分，结果如表2所示.

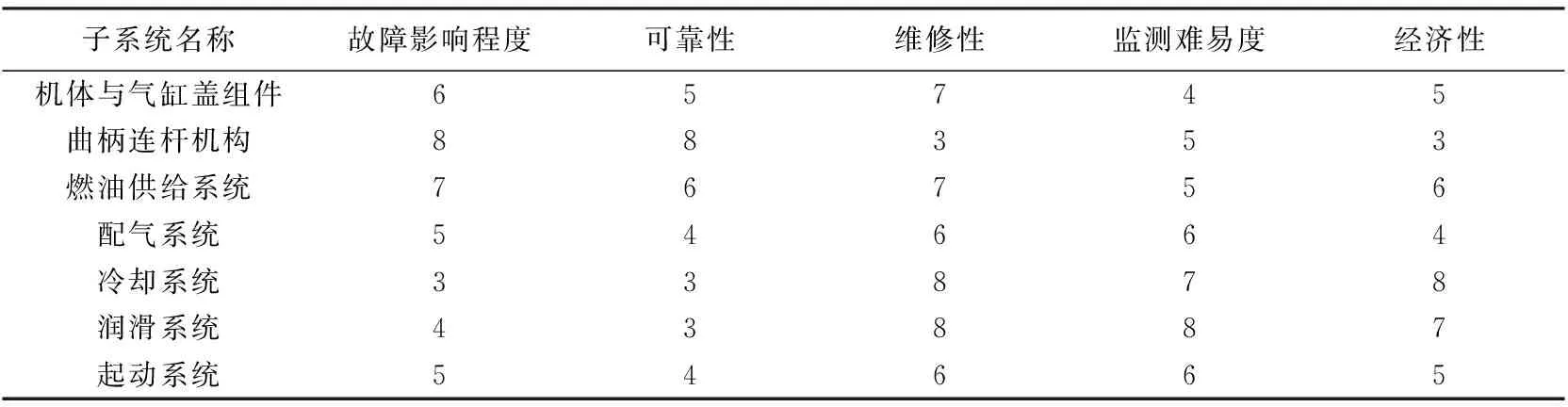
表2　影响因素评分结果

2.3子系统重要度评价

评分完成后，即可利用投影寻踪分类模型对各子系统重要度进行排序.首先，将评分结果按式(19)进行无量纲处理，结果如表3所示.

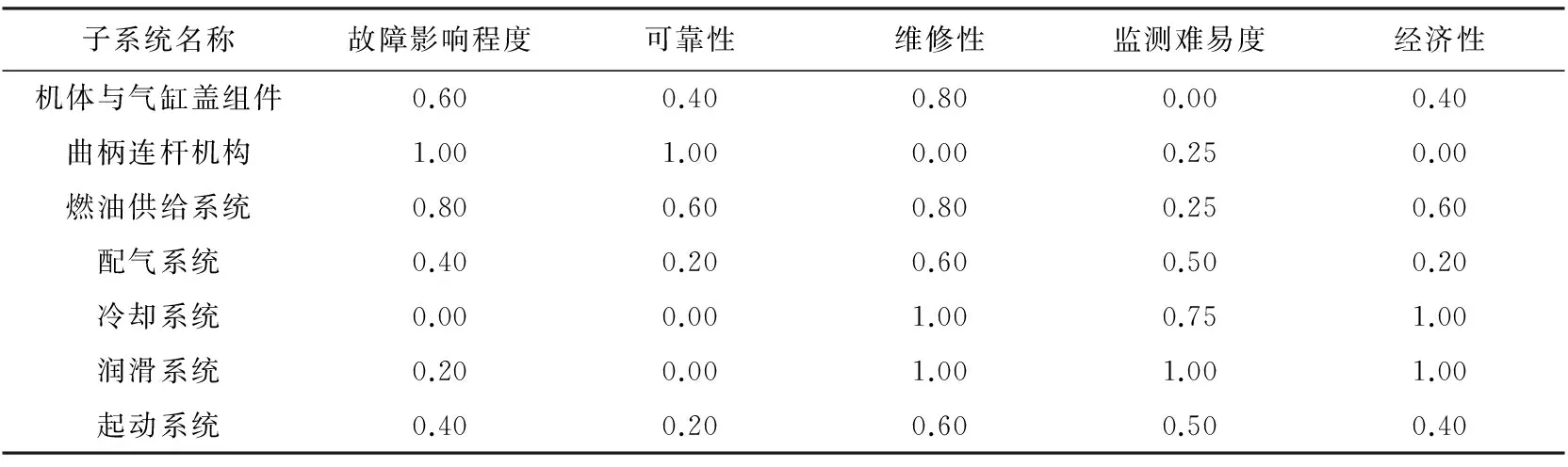
表3　影响因素评分结果归一化

然后，将归一化序列{x(i,j)}代入式(22)～式(24)，即可得到投影指标函数，利用遗传算法求解由式(25)和式(26)所确定的优化问题，步骤如下：

1) 随机产生p=500组初始单位投影方向向量a*，按式(1)分别计算p组n维向量的投影特征值z*(i)；

2) 分别计算每组投影方向上的Sz和Dz，进而根据式(2)计算每组投影方向上的目标函数值Q(a)；

3) 通过遗传算法中的选择、交叉和变异操作，产生3×p组新的投影方向向量a*；

4) 根据Q(a)值越大越优的原则，从3×p组投影方向向量中选取新的投影方向向量，回到第(1)步，重新计算z*(i)；

5) 当目标函数值Q(a)不再增大时所对应的投影方向向量就是最优投影方向a*.

按上述步骤可求得柴油机测试性设计时各子系统重要度评价最佳投影方向为a*=(0.036,0.023,0.660,0.516,0.544)，各子系统重要度评价的最终投影值为z*(i)=(0.776,0.188,1.026,0,782,1.720,0.891)，结果如图2所示.

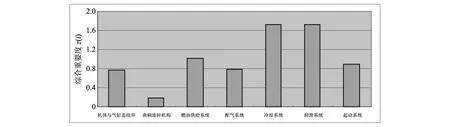
图2　柴油机各子系统重要度投影值Fig.2　Projection value of diesel engine subsystem importance

可以看出各子系统重要度排序为：冷却系统和润滑系统的重要度最高，起动系统、燃油系统和配气系统的综合重要度分列其后，最后是机体与气缸盖组件和曲柄连杆机构.

3　机械装备测试性分配实施

仍以上述柴油机测试性分配为例说明机械装备测试性分配实施的具体过程.对柴油机而言，不同类型的柴油机故障发生概率基本相似，因此，可参考已有成熟机型的故障率数据.本文以某型柴油机故障率数据为基础来确定新研制柴油机测试性分配方案，数据如表4所示[5].

表4　柴油机子系统故障率数据

测试性分配实施步骤：首先，根据各子系统故障率数据，按式(7)求得各子系统的βiD；然后，根据投影寻踪求得各子系统重要度，按式(15)计算各子系统故障检测率的降额度εiD；再根据式(16)求得各子系统的分配因子；最后，即可根据式(6)求得各子系统分配的故障检测率指标γFDi.同理，可求得各子系统分配的故障隔离率指标γFIi.具体数据如表5所示.

表5　测试性分配结果

由上述分配结果可知，冷却和润滑系统的重要度最大，但由于二者故障率较低，最终分配的测试性指标并不是最大的；曲柄连杆机构虽然重要度最低，但由于故障率最高，分配的测试性指标较大.可见，该方法能够体现重要度在测试性分配中的作用，让故障率较低的冷却和润滑系统的测试性指标得到了提高，这与实际情况中设计人员重视冷却和润滑系统测试性设计的初衷是一致的.

4　结　论

本文在借鉴可靠性分配模型的基础上，建立了机械装备测试性分配模型，并将测试性分配问题转化为求分配因子；分配因子求解过程中，提出了基于投影寻踪的子系统重要度评价方法，以子系统重要度为基础，求得分配因子，最终得到各子系统测试性指标.论文以柴油机为对象进行了测试性分配实例实施，分配结果为：冷却和润滑系统由于故障率较低，尽管重要度最大，分配的测试性指标并不是最大；曲柄连杆机构虽然重要度最低，但由于故障率最高，分配的测试性指标最大，体现了子系统重要度在测试性分配中的作用.

[1]田仲.测试性分配方法研究[J].北京航空航天大学学报，1999，25(5)：607-610.

Tian Zhong.Research on testability allocation method[J].Journal of Beijing University of Aeronautics and Astronautics，1999，25(5):607-610.(in Chinese)

[2]李金龙，陶凤和，贾长治，等.基于AHP的测试性分配方法研究[J].中国测试，2010，36(2)：30-33.

Li Jinlong，Tao Fenghe，Jia Changzhi，et al.Study on testability allocation method based on analytic of hierarchy process[J].China Measurement & Test，2010，36(2):30-33.(in Chinese)

[3]沈亲沐.装备系统级测试性分配技术研究及应用[D].长沙：国防科技大学，2007.

[4]Fu Q，Liu J Y，Wang L K.Study on the PPE model based on RAGA to classify the county energy[J].Journal Systems Science and Information，2004，2(1):73-82.

[5]高晓清.基于多传感器信息融合的柴油发动机故障诊断研究[D].太原：中北大学，2008.

Research on Mechanical Equipment Testability Allocation Method Based on Projection Pursuit

ZHOU Ping1，LIU Jielin1，LIU Dongfeng2

(1.PLA Unit No.92557，Guangzhou 510720，China；2.Qingdao Oil Analysis Centre，Naval University of Engineering，Qingdao 266012，China)

Reliability of distribution modeling method,mechanical equipment testability allocation model was firstly established.Then translate the testability allocation problem into seeking distribution factor; Pojection pursuit method was proposed to evaluate subsystem importance,And based on subsystem importance acquired the distribution factor of each subsystem,the subsystem distribution factor is obtained and the test index is finally assigned.Finally,a diesel engine allocation example was given as an example,the allocation result dedicate the testability allocation method proposed in this paper is reasonable.

testability of mechanical equipment；index allocation；projection pursuit；distribution factor

1671-7449(2016)05-0450-07

2016-01-09

周平(1982-)，男，工程师，博士，主要从事机械设备状态监测与故障诊断的研究.

TP206

Adoi：10.3969/j.issn.1671-7449.2016.05.015