一类广义平均曲率Rayleigh方程周期解存在性与唯一性
兰德新,陈鹭杰,陈文斌
(武夷学院数学与计算机学院,福建武夷山354300)
一类广义平均曲率Rayleigh方程周期解存在性与唯一性
兰德新,陈鹭杰,陈文斌
(武夷学院数学与计算机学院,福建武夷山354300)
主要运用Mawhin重合度拓展定理研究了一类广义平均曲率Rayleigh方程周期解存在性与唯一性问题,得到了周期解存在性与唯一性的相关新结果。
广义平均曲率;Rayleigh方程;周期解;重合度
考虑如下一类广义平均曲率Rayleigh方程:

这里f,e:R→R,g:R×R→R是连续函数,f(0)=0,e是以T为周期的函数,g是第一分量且以T为周期的函数,T>0.众所周知,Rayleigh方程的动力特性在一些领域上的应用,如物理、力学和工程技术领域,而被广泛研究[1-3]。在这些领域的应用,最重要的是Rayleigh方程周期解存在性与唯一性。例如文献[4]讨论了受迫Rayleigh-type方程周期解存在性与唯一性,并得到如下结果:
定理A考虑如下Rayleigh方程:
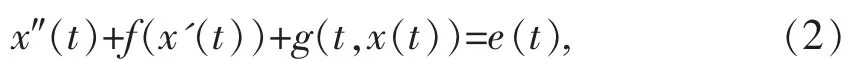
这里f,e:R→R,g:R×R→R是连续函数,f(0)=0,e是以为T周期的函数,g是第一分量且以T为周期的函数,T>0。假设存在非负常数d,m1和m2满足:
(A1)对所有t∈R,x1,x2∈R且x1≠x2都有

(A2)对所有有x(g(t,x)-e(t))<0,
(A3)对所有t,x∈R,有
则方程(2)有唯一周期解。
1 预备知识
在本文中,设X和Y是实的Banach空间,令L∶D(L)⊂X→Y是一个指标零的Fredholm算子,其中D(L)表示L的定义域。这意味Im L在Y上封闭,且dim KerL=dim(Y/Im L)<+∞。考虑余子空间X1和Y1使得X=KerL⊕X1和Y=Im L⊕Y1,令P∶X→KerL和Q∶Y→Y1是自然投影,很显然,KerL∩(D(L)∩X1)=0。所以限制Lp∶=L|D(L)∩X1是可逆的,用K表示Lp的逆。
引理1[8]假设X和Y是两个Banach空间,且L∶D(L)⊂X→Y是一个指标零的Fredholm算子,而且Ω⊂X是有界开集和上是L紧的。
假设:
(1)Lx≠λNx,∀(x,λ)∈(D(L)∩∂Ω)×(0,1);
(2)Nx∉Im L,∀x∈KerL∩∂Ω;
(3)deg(JQN,Ω∩KerL,0)≠0这里J∶Im Q→KerL是一个同构。
运用Mawhin重合度拓展定理来研究方程(1)的周期解存在性,为此考虑如下系统:
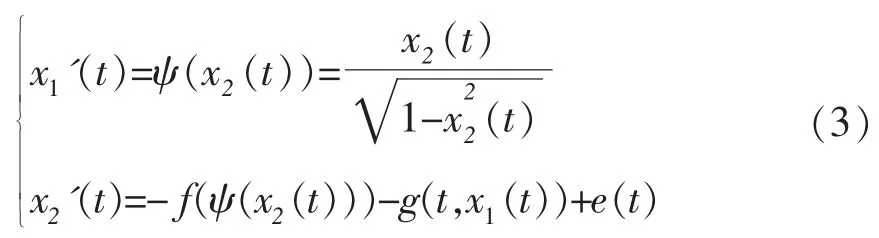
令X=Y={x:x=(x1,x2)T∈C(R,R2),x(t)≡x(t+T)},‖x‖=max{|x1|0,|x2|0},其中。显然,X和Y是两个Banach空间。
同时,令
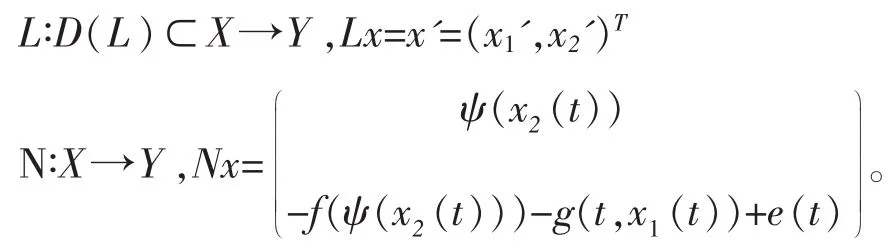
易知方程组(3)被转换成抽象的方程Lx=Nx。此外,从L的定义,我们知道所以L是一个指标零的Fredholm算子。
另外,定义投影算子P∶X→KerL和Q∶Y→Im Q为

设K表示LKerP∩D(L)的逆算子。则有KerL=Im Q=R2和
2 主要结果
证明首先考虑Lx=λNx,∀λ∈(0,1)。令Ω1={x∈X:Lx=λNx,λ∈(0,1)}。
如果x∈Ω1,则有

由(4)式中的第一个方程,我们有

由此得出
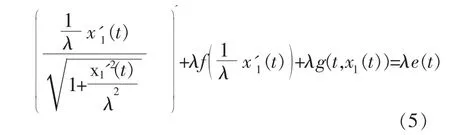
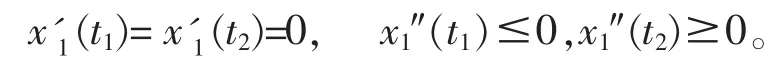

再由条件(A2)的假设,有x1(t1)<d和x1(t2)>-d。因此由x1(t)的周期性,我们得到

这意味着x1(t)是有界的,即|x1|0<d。
进一步,从(4)式中的第一个方程,得到

这意味着存在一个常数ζ∈[0,T]使得x2(ζ)=0。
所以
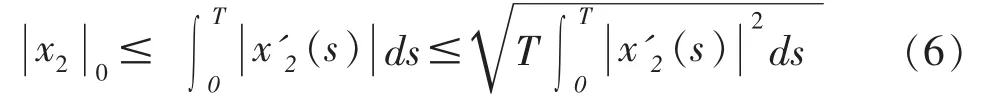
由(4)式的第二个方程的两边同乘以x'2(t)后在区间[0,T]上积分得
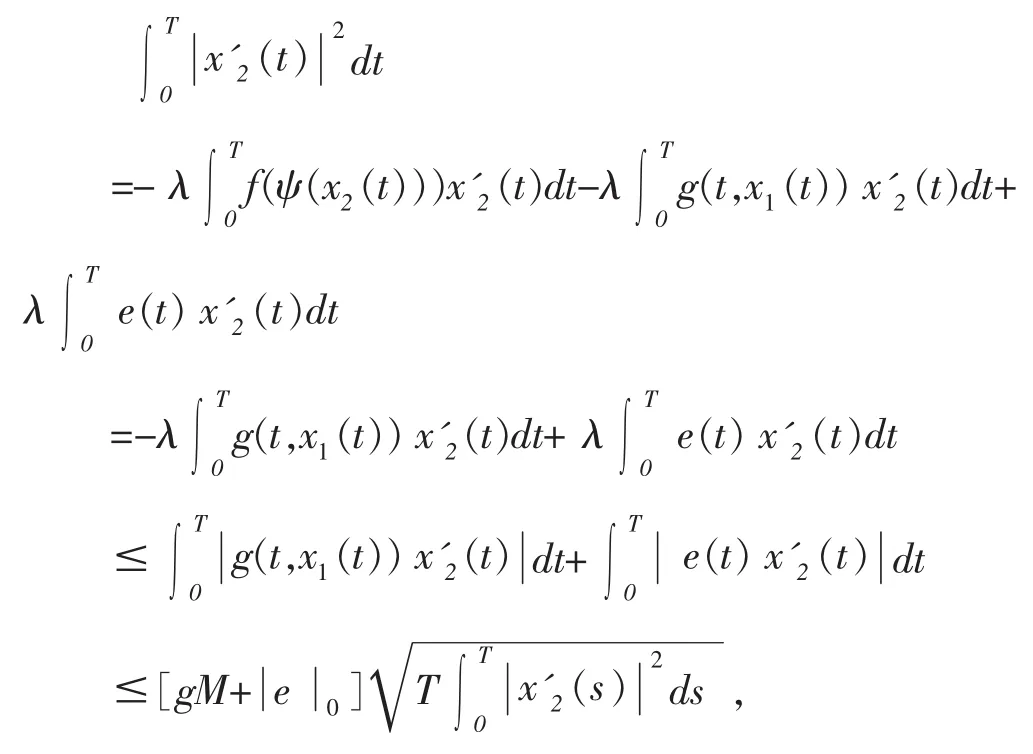


令Ω2={x:x∈Ker L,QNx=0}。则易得x2(t)=0≤d0。
因此引理1的条件(1)和(2)是满足的。然后再验证引理1的条件(3)。
为此令J:Im Q→Ker L,J(x1,x2)=(x1,x2),易知对任意小的ε>0,方程QN(x)=(0,0)T,也就是

在(Ω∩KerL)/Δε上没有解,其中ε∈(0,ε0)是任意常数。
所以deg{JQN,Ω∩Ker L,0}=deg{JQN,Δε,0}。令
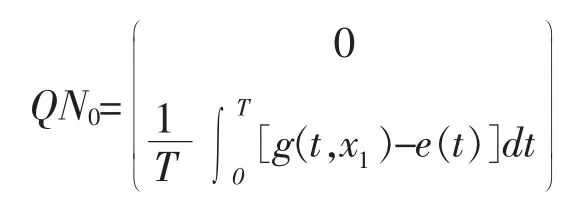
如果x∈∂Δε,则有
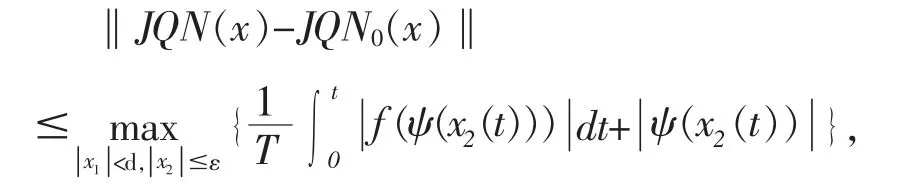
这意味着当ε→0时有‖JQN(x)-JQN0(x)‖→0。所以若取充分小ε>0,则有deg{JQN,Δε,0}=deg{JQN0,Δε,0}
注意到dim QN0=1,由此得出deg{JQN0,Δε,0}= deg{JQN0,Δ0,0},其中是常数。
再由条件(A2)的假设得知deg{JQN0,Δ0,0}≠0,也就是
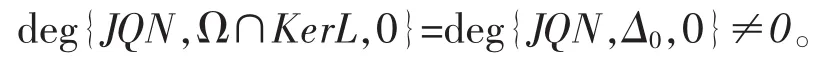
因此引理1条件(3)也是满足的。所以,应用引理1,推出方程上至少有一个周期解x1(t)。
其次证明唯一性,假设条件(A1)成立。令x3(t)和x4(t)是方程(1.1)的两个不同的周期解,并设
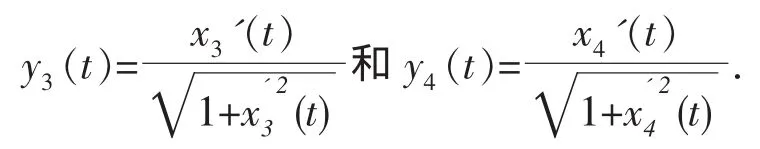

下面验证对∀t∈[0,T],有u(t)≤0。
假设这里存在t0∈[0,T]使得

则u'(t0)=ψ(y3(t0))-ψ(y4(t0))=0,这意味着y3(t0)=y4(t0)和u″(t0)≤0。

而由条件(A1)和y3(t0)=y4(t0)得出这是矛盾的,因此maxt∈[0,T]u(t)≤0。
同理可得,将x3和x4互换角色,即可得出maxt∈[0,T]u(t)≥0.这就意味着u(t)≡0,也就是说x3(t)≡x4(t)。
所以方程(1)最多有一个解。这样定理1可证。
3 例子
在物理、力学和工程技术的实际应用中,考虑如下Rayleigh方程:
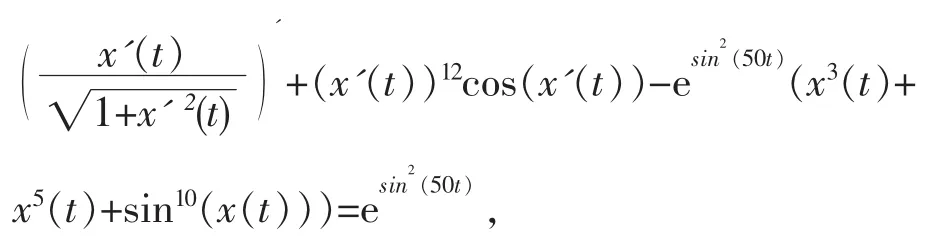
这里f(x)=x12(t)cos(x(t)),g(t,x)=-esin2(50t)((x3(t)+x5(t)+ sin10(x(t)))和e(t)=esin2(50t)。应用定理1,推算得d=1,。容易验证条件(A1)和(A2)是成立的,应用定理1得上述方程有唯一的周期为的周期解。
[1]Hale JK.Theory of functional differential equations[M].New York:Springer-Verlag,1977.
[2]Antosiewicz H A.On nonlinear differential equations of the second order with integrable forcing term[J].J.Lond.Math.Soc,1955(30):64-67.
[3]Sansone G,Conti R.Non-linear differential equation[M].New York:MacMillan,1964.
[4]Gao H,Liu BW.Existence and uniqueness of periodic solutions for forced Rayleigh-type equations[J].Applied Mathe matics and computation,2009(211):148-154.
[5]Bonheure D,Habets P,Obersnel F.Classical and non-classical solutions of a prescribed curvature equations[J].J.Differential Equations,2007(243):208-237.
[6]Lopez R.A comparison result for radial solutions of themean curvature equation[J].Appl.Math.Lett,2009(22):860-864.
[7]Pan H.One-dimensional prescribed mean curvature equation with exponentialnonlinearity[J].Nonlinear Annl,2009(70):999-1010.
[8]Gaines R E,Mawhin J.Coincidence degree and nonlinear differential equaations[M].New York:Springer-Berlin.1977.
(责任编辑:叶丽娜)
Existence and Uniqueness of Periodic Solutions for a Kind of Prescribed Mean Curvature Rayleigh Equation
LAN Dexin,CHEN Lujie,CHENWenbin
(School of Mathematics and Computer Science,WuyiUniversity,Wuyishan,Fujian 354300)
In this paper,we use the coincidence degree theory to establish new results on the existence and uniqueness of T-periodic solutions for a kind of prescribed mean curvature Rayleigh equation of the form
prescribed mean curvature;Rayleigh equation;periodic solution;coincidence degree
O175
A
1674-2109(2016)06-0061-04
2016-02-27
福建省中青年教师教育科研项目(JA15524)。
兰德新(1964-),男,畲族,副教授,主要从事应用数学的研究。

