CO-OFDM系统中基于线性预处理的新相位噪声抑制算法

李玲香，李季碧

(1.湖南科技学院 电子与信息工程学院，湖南 永州 425199； 2.重庆邮电大学 通信与信息学院，重庆 400065)



CO-OFDM系统中基于线性预处理的新相位噪声抑制算法

李玲香1，李季碧2

(1.湖南科技学院 电子与信息工程学院，湖南 永州 425199； 2.重庆邮电大学 通信与信息学院，重庆 400065)

针对相干光正交频分复用(coherent optical orthogonal frequency division multiplexing, CO-OFDM)系统中相位噪声引起的载波间干扰(inter-carrier interference, ICI)问题，提出了一种基于线性预处理的新判决反馈相位噪声抑制算法。该新算法改进了线性预处理部分，利用循环前缀与OFDM符号固有的相关性，在时域进行简单的线性组合运算，充分利用了OFDM符号中冗余信息。仿真分析表明，在激光器线宽为200 kHz且误码率(bit error rate, BER)为10-4时，与判决反馈相位噪声抑制算法和一次迭代的判决反馈相位噪声抑制算法相比，该新算法BER曲线的信噪比(signal to noise ratio, SNR)分别改善了3 dB和1 dB，有效地降低由ICI引起的错误平层。

相干光正交频分复用(CO-OFDM)；相位噪声；线性预处理；载波间干扰(ICI)；误码率(BER)

0　引　言

光通信系统中相干光正交频分复用(coherent optical orthogonal frequency division multiplexing, CO-OFDM)技术是一项最具发展前景的技术之一，因它能有效对抗由色度色散(chromatic dispersion, CD)和偏振模色散(polarization-mode dispersion, PMD)引起的符号间干扰[1-2]。但是相位噪声会对(orthogonal frequency division, OFDM)符号产生公共相位误差(common phase error, CPE)与载波间干扰(inter-carrier interference, ICI)的影响，进而破坏子载波正交性。这会导致系统误码率性能变差，出现错误平层[3-4]。因而，相位噪声抑制算法的研究对CO-OFDM系统具有重要的意义。相位噪声对OFDM的影响已经被广泛地研究[5-7]。研究者们根据相位噪声影响和OFDM符号结构特点，在传统导频辅助算法的基础上，不断进行改进和延伸。到目前为止，按相位噪声抑制算法结构特点可分为如下几类[8-10]：导频辅助类、数据辅助类、判决反馈类和盲估计类。判决反馈类算法能够有效抑制CPE和ICI，且易实现[6]。判决反馈类相位噪声在大的相位噪声情况下或采用高阶调制形式的情况下，易出现判决误差[6]。

本文将在判决反馈相位噪声抑制(decision feedback phase noise suppression，DF-PNC)算法的基础上进行改进，提出一种基于线性预处理的新判决反馈相位噪声抑制算法。该算法先在时域上对OFDM符号进行线性预处理过程，然后在接收端经快速傅里叶变换(fast fourier transform, FFT)之后，对预处理过的OFDM符号进行判决反馈相位噪声抑制。

1　CO-OFDM系统与相位噪声模型

图1给出了具有相位噪声的基带CO-OFDM系统基本框图。其中，P/S为并串变换；S/P为串并变换。频域发送OFDM符号X=[X(1)X(2)…

X(N)]T经IFFT后得到时域信号z=[z(1)z(2)

…z(N)]T，其中，T表示转置。假设OFDM子载波信号是均值为0，方差为ES的相互独立的随机变量，则Ε{X(m1)X*(m2)}=ESδ(m1-m2)，其中，*表示复共轭。

在接收端，假设时间和频率都同步，则接收到的频域符号表示为[8]

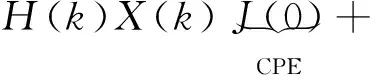
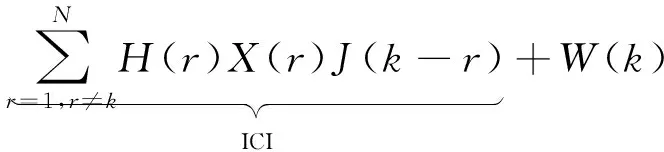
(1)

(1)式中，系数J(0)作用在所有的载波上，即为CPE；第2项即为ICI，受J(k)的高阶系数影响而产生。

可把(1)式表示为

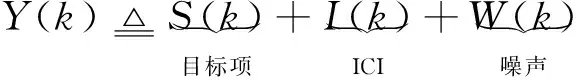
(2)

(1)-(2)式中：W(k)为相应的频域噪声；H(k)为信道频域响应；J(k)为相位噪声的傅里叶变换过程，表示为

(3)

相位噪声φ(n)模拟为维纳过程[11]，表示为

(4)

(4)式中：v(n)为相邻子载波间的相位偏差，这是一个高斯随机变量：v(n)～Ν(0,2πΔf/fs)。其中，Δf为发送和接收激光器线宽总和，fs为数模变换采样频率。

图1　具有相位噪声的CO-OFDM基本框图Fig.1　Block diagram of CO-OFDM systems with the phase noise

2　判决反馈相位噪声抑制算法

相位噪声对OFDM符号造成的CPE影响对OFDM符号内所有载波产生相同的相位旋转，则可利用导频符号发送前后的相位差值对CPE影响进行纠正。当相位噪声较小时，ICI的影响较小，可以忽略。因此，对于受到相位噪声影响的接收OFDM符号，可表示为[6]

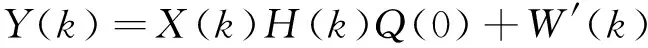
(5)

(6)

根据(6)式，利用最小平方准则(least squares criterion,LS)得到相邻导频相位偏差初始值为

(7)

(7)式中：QP(0)为相邻导频相位偏差初始值；(·)*为共轭运算；Sp为导频信号；H(k)在信道估计中由训练序列进行估值，此处假设已进行正确信道估计过程。

当相位噪声较严重时，OFDM符号受ICI影响较严重，此时需考虑ICI的影响。根据最小均方误差(minimum mean squared error,MMSE)准则，频域均衡系数表示为

(8)

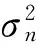
(9)

(9)式中：NN，SN分别表示虚拟子载波数目与所有虚拟子载波的集合。

根据MMSE准则，得纠正后的估计符号为

(10)

由于导频数过少，估计出的Q(0)不精确；而导频数太多，频带利用率降低。因而，为了提高判决反馈相位噪声抑制算法中对Q(0)估值精确性，提出了迭代更新的判决反馈相位噪声抑制算法。迭代判决反馈相位噪声抑制算法的计算过程如下：首先，用导频符号对Q(0)进行估值，然后，利用此估计值校对数据子载波进行校正，在一定程度上改善系统性能。特别是在大信噪比时，采用估计值Q(0)对数据子载波进行CPE校正后，此时的OFDM符号误码率较低。因此，可利用校正后的数据子载波对Q(0)做进一步的估计。采用导频符号对数据子载波进行初次校正后，对校正后的数据子载波进行判决处理，根据(11)式对判决后的数据符号进行二次CPE估值，得到CPE的二次估值QD(0)，最后，根据2次CPE估值，进行优化得出最终的CPE估值并对数据子载波进行重新校正。

(11)

(11)式中，SD为判决后的数据子载波。

(12)

利用优化出的估计值对OFDM数据符号进行校正，计算如下

(13)

(13)式中，优化因子P的取值为0～0.1。

3　基于线性预处理的一种新判决反馈相位噪声抑制算法

判决反馈相位噪声抑制算法对CPE与ICI都有抑制作用，性能较好，且实现简单。但其在相位噪声较大的情况下，易发生错误判决噪声错误累积，系统的抗噪性能不强[12]。随后的迭代判决反馈相位噪声抑制算法需进行多次迭代计算，算法复杂且抗噪性能提升不大。因此，本文在判决反馈相位噪声抑制算法的基础上提出了一种基于线性预处理的新判决反馈相位噪声抑制算法。该新算法能有效利用循环前缀中的信息，进一步提升原有算法的相位噪声抑制性能，计算简单，易实现。

3.1一种新判决反馈相位噪声抑制算法

众所周知，OFDM符号中的循环前缀部分即为OFDM符号末尾处的重复采样。本算法的核心思想就是充分利用传输过程中的循环前缀与OFDM符号固有的相关性，将此循环前缀中的部分与OFDM发送符号中的部分在时域进行有效的线性组合预处理，然后，在频域采用原有的判决反馈相位噪声抑制算法对OFDM符号进行相位噪声抑制。循环前缀在传输过程中占有一定的带宽，而在接收端又被丢弃，本论文的改进算法正是充分利用循环前缀的信息，提高相位噪声抑制算法性能，具体的框架图如图2所示。

图2中，在基于判决反馈的相位噪声抑制算法的基础上，先将OFDM符号与部分循环前缀信息进行线性组合预处理。其中，线性预处理部分的结构如图3所示。最后得到的长度为q的循环前缀信息实际上来源于原OFDM发送符号的最末q个采样信息符号，此两者之间存在相关性，因此，将此部分循环前缀信息与接收到的部分OFDM符号进行线性组合，从而改善判决反馈相位噪声抑制算法的相位噪声抑制性能，进一步改善系统性能。为方便起见，这里定义q=Ncp-L+1，L为循环前缀中未被利用的部分；最后接收到的长度为q的循环前缀部分，r(-q),…,r(-1)是将要进行线性组合预处理的部分。组合后的信号vt(n)可表示为

υt(n)=

(14)

图2　线性预处理过程的系统框图Fig.2　Block diagram for the linear preprocessing process

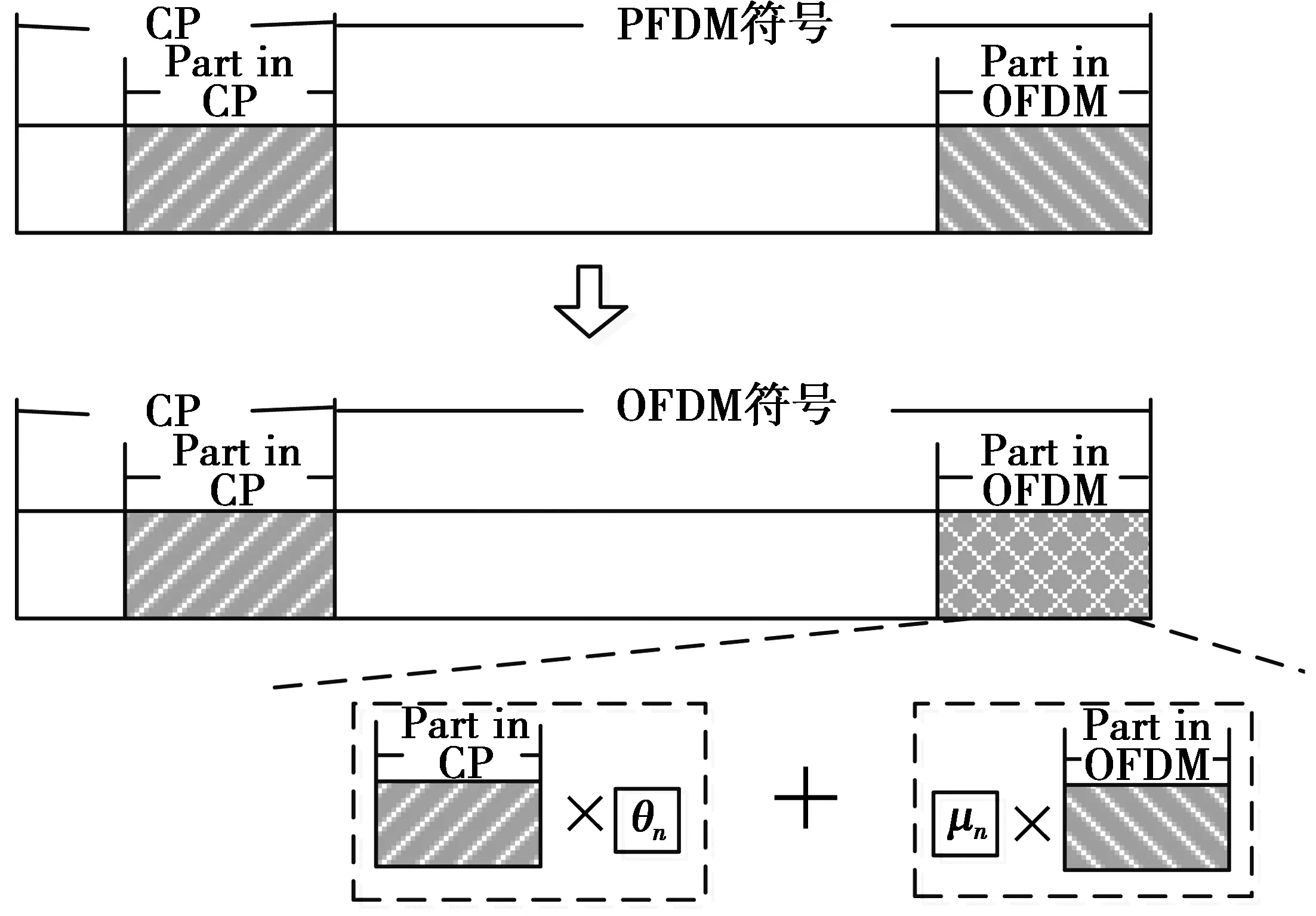
图3　线性预处理过程结构示意图Fig.3　Schematic diagram for the linear preprocessing process

(15)

(15)式的系数约束条件，即所谓的奈奎斯特约束条件，确保在没有相位噪声情况下的正交性。根据(4)式所示的相位噪声数学模型，经过进一步繁琐的推论计算可得到线性系数表示为

(16)

(17)

(18)

(18)式中:fs为模数变换的采样频率；T为OFDM符号周期；Δf为激光器线宽。

3.2仿真分析

以MATLAB仿真软件进行仿真实验，基本的仿真参数设计如下：OFDM符号总的子载波数N为512，其中，有效子载波数为384路，导频子载波数NP为16路，数据子载波与导频子载波都采用16-QAM或4-QAM调制方式进行对比分析，剩余的112路则为虚拟子载波；循环前缀长度NCP为128，为总载波数的1/4；采样率为24 GHz；OFDM符号数为2 000；OFDM符号周期T=37.9 ns；仿真实验过程中采用的发送端和接收端的激光器线宽Δf分别为2，20，200 kHz等，便于对比分析。另外，改进算法中选用的循环前缀的长度因子q值分别为25，50，75与100。在本文中，基于线性预处理所提出的新判决反馈相位噪声抑制算法记作LP-DF-PNC。

本文仿真主要分为3组进行对比分析：①在激光器线宽Δf=200 kHz时，LP-DF-PNC算法在选取的部分循环前缀长度因子q不同情况下的误码率性能对比分析；②OFDM符号采用16-QAM调制形式，在不同程度的相位噪声情况下，对DF-PNC算法、一次迭代的DF-PNC算法(即DF-PNC-1算法)、LP-DF-PNC算法进行误码率性能对比分析。③在激光器线宽Δf=200 kHz时，以4-QAM和16-QAM调制为例，针对不同调制方式的OFDM符号，分别采用DF-PNC算法、DF-PNC-1算法与LP-DF-PNC算法进行相位噪声抑制后对应的误码率性能对比分析。

图4为在激光器线宽为Δf=200 kHz时，选取的部分循环前缀长度因子q不同时，LP-DF-PNC算法的误码率性能曲线对比图。从图4中可以看出，随着q长度的增加，LP-DF-PNC算法的误码率性能逐渐改善，说明选取q值长度越大，相应的LP-DF-PNC算法的相位噪声抑制性能越好。当选取的长度因子q等于循环前缀的长度时，即q=128时，LP-DF-PNC算法的误码率性能最好；另一方面，q值增加时，说明参与计算的循环前缀符号个数在增加，则相应的计算量也会增大。因而在本文实验中，折中考虑长度因子q值都设定为100。

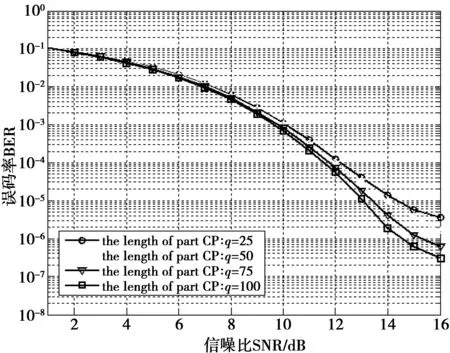
图4　不同循环前缀长度因子q时， LP-DF-PNC 改进算法的误码率性能曲线对比图Fig.4　Contrast figure of the BER performance curve for the improved LP-DF-PNC algorithm at the different cyclic prefix length factor q

图5是以16-QAM调制方式为例，在不同程度的相位噪声情况下，本文改进算法与另外2种算法的误码率性能对比图。由图5可知，当激光器线宽Δf=20 kHz时，LP-DF-PNC算法误码率性能优于另外2种算法，且超过了没有相位噪声时的误码率曲线的边缘。当激光器线宽Δf=200 kHz，LP-DF-PNC算法在误码率为10-4时，与DF-PNC算法相比，性能提升了3 dB，而与DF-PNC-1算法相比，性能提升了1 dB，有效地降低由ICI引起的错误平层。

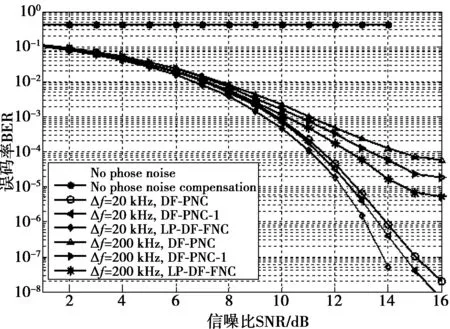
图5　不同程度相位噪声时，改进算法与 原有算法的误码率性能曲线对比图Fig.5　Contrast figure of the BER performance curve between the improved algorithm and the original algorithm at the different degree of the phase noise

图6为在激光器线宽Δf=200 kHz时，3种算法在不同调制情况下的误码率曲线对比图。由图6可知，在4-QAM调制情况下，3种算法的误码率性能较接近，改善不大。这是因为4-QAM调制欧氏距离较大，在相位噪声不是特别严重的情况下，经相位噪声抑制算法处理后，星座点都能在判决范围内，在接收端不易发生错误判决。在16-QAM调制的情况下，三者之间的误码率曲线性能差距变得逐渐明显。这说明本文改进的LP-DF-PNC算法更适合于高阶调制的情况。

图6　不同调制时，改进算法与原有算法的 误码率性能曲线对比图Fig.6　Contrast figure of the BER performance curve between the improved algorithm and the original algorithm at the different modulation conditions

图7　进行相位噪声抑制后对应误码率曲线对比图Fig.7　Contrast figure of the corresponding BER curve after suppressing the phase noise

图7为LP-DF-PNC算法与DF-PNC算法对不同级别相位噪声的容忍度。由图7可知，本文所改进的LP-DF-PNC算法具有更优的相位噪声容忍度。特别是在激光器线宽Δf=50 kHz及其以下时，LP-DF-PNC算法的误码率低于没有相位噪声情况的误码率。这是因为LP-DF-PNC算法不仅对相位噪声具有抑制作用，同时还能对部分的加性高斯随机噪声具有抑制作用。

4　结　论

本文为了改善相干光正交频分复用通信系统中相位噪声引起的载波间干扰问题，在判决反馈相位噪声抑制算法的基础上提出了一种基于线性预处理的新判决反馈相位噪声抑制算法。该新算法充分利用传输过程中的循环前缀与OFDM符号固有的相关性，将此循环前缀中的部分与OFDM发送符号中的部分在时域进行有效的线性组合预处理，然后在频域采用原有的判决反馈相位噪声抑制算法对OFDM符号进行相位噪声抑制。仿真分析表明，本文所提出的新算法在不需要额外增加辅助信息的前提下，既能有效地改善相位噪声抑制性能，还能对加性高斯随机噪声具有部分抑制作用。

[1]ZHAO C, YANG C, YANG F, et al. A CO-OFDM System With Almost Blind Phase Noise Suppression[J]. IEEE Photonics Technology Letters, 2013, 25 (17): 1723-1726.

[2]HONG X, HONG X, HE S. Linearly interpolated sub-symbol optical phase noise suppression in CO-OFDM system[J]. Optics Express,2015, 23(4):4691-4702.

[3]YUAN Jianguo, BI Wenjuan, BI Wenjie, et al. A Novel Two-stage Phase Noise Estimation Algorithm for Coherent Optical OFDM Systems[J]. OPTIK, 2013, 124(24):7053-7055.

[4]YI X W, SHIEH W, MA Y. R. Phase noise effects on high spectral efficiency coherent optical OFDM transmission[J]. J Lightw Technol, 2008, 26(10): 1309-1316.

[5]HA Youngsun, CHUNG Wonzoo. Non-Data-Aided Phase Noise Suppression Scheme for CO-OFDM Systems[J]. IEEE Photonics Technology Letters, 2013, 25(17): 1703-1706.

[6]CAO Shengjiao, KAM Pooi Yuen, YU Changyuan. Decision-Aided, Pilot-Aided, Decision-Feedback Phase Estimation for Coherent Optical OFDM Systems[J]. IEEE Photonics Technology Letters, 2012, 24(22): 2067-2069.

[7]袁建国，毕文娟，胡云霞，等. CO-OFDM系统中基于维纳滤波的相位噪声ICI抑制算法[J]. 光电子.激光，2014, 25(2):259-263.

YUAN Jianguo, BI Wenjuan, HU Yunxia, et al. Phase noise ICI suppression algorithm based on Wiener filter in CO-OFDM systems[J]. Journal of Optoelectronics.Laser, 2014, 25(2):259-263.

[8]RANDEL S, ADHIKARI S, JANSEN S. Analysis of RF-Pilot-Based phase noise compensation for coherent optical OFDM systems[J]. IEEE photonics technology letters, 2010, 22(17):1288-1290.

[9]NGEBANI I, LI Y, XIA X G, et al. Analysis and Compensation of Phase Noise in Vector OFDM Systems[J]. IEEE Transactions on Signal Processing, 2014, 62(23): 6143-6157.

[10] MOUSA-PASANDI M, PLANT D. Noniterative interpolation-based partial phase noise ICI mitigation for CO-OFDM transport systems[J].IEEE Photonics Technology Letters, 2011, 23(21): 1594-1596.

[11] TANG Y, SHIEH W, YI X, et al. Optimum design for RF-to-optical up-converter in coherent optical OFDM systems[J]. IEEE Photonics Technology Letters, 2007, 19(7): 483-485.

[12] LEE M K, YANG K, CHEUN K. Iterative receivers based on subblock processing for phase noise compensation in OFDM systems[J]. IEEE Transactions on Communications, 2011, 59(3):792-802.

李玲香(1976-)，女，湖南郴州人，讲师，硕士，主要研究方向为移动通信。E-mail：lilingxiang2013@hotmail.com。

李季碧(1975-)，女，四川开江人，讲师，硕士，主要研究方向为无线通信网。E-mail:lijb@cqupt.edu.cn。

(编辑：刘勇)

s：The National Natural Science Foundation of China(61472464); The Key discipline construction project funding for Hunan University of Science and Engineering(Circuits and Systems)

Novel phase noise suppression algorithm based on the linear preprocessing in CO-OFDM systems

LI Lingxiang1，LI Jibi2

(1.School of Electronics and Information Engineering ,Hunan University of Science and Engineering, Yongzhou 425199, P.R. China;2.Shool of Communication and Information Engineering, Chongqing University of Posts and Telecommunications,Chongqing 400065, P.R.China)

A novel decision feedback phase noise suppression algorithm based on the linear preprocessing is proposed according to the Inter-Carrier Interference (ICI) problem caused by the phase noise in the coherent optical orthogonal frequency division multiplexing (CO-OFDM) systems. The novel algorithm has improved the linear preprocessing, the inherent correlation between the cyclic prefix and the OFDM symbol is applied to make a simple linear combination operation in time domain, and the novel algorithm can make full use of the redundant information in the OFDM symbol. The simulation analysis shows that the signal to noise ratio (SNR) of the BER curve of the novel algorithm, compared with the decision feedback phase noise suppression algorithm and an iteration of the decision feedback phase noise suppression algorithm, can respectively be improved 3 dB and 1 dB when the bit error rate (BER) is of 10-4and the laser line width is of 200 kHz. Therefore, the proposed algorithm can effectively reduce the error floor caused by the ICI.

coherent optical orthogonal frequency division multiplexing(CO-OFDM); phase noise; linear preprocessing; inter-carrier interference(ICI); bit error rate(BER)

10.3979/j.issn.1673-825X.2016.05.020

2016-05-03

2016-09-13通讯作者：李玲香lilingxiang2013@hotmail.com

国家自然科学基金(61472464)；湖南科技学院重点学科建设项目(电路与系统)

TN929.11

A

1673-825X(2016)05-0743-06