循环荷载下饱和软黏土累积变形遗传分数阶导数开尔文模型

张秋瑾 ,姚兆明 ,姜自华, 王春萌

(安徽理工大学土木建筑学院，安徽　淮南　232001)



循环荷载下饱和软黏土累积变形遗传分数阶导数开尔文模型

张秋瑾 ,姚兆明 ,姜自华, 王春萌

(安徽理工大学土木建筑学院，安徽淮南232001)

研究循环荷载作用下饱和软黏土的累积变形对计算交通荷载引起的地基沉降具有重要意义。对饱和软黏土分别进行围压为100kPa、150kPa、200kPa的等向固结动应力比为0.1、0.2和偏压固结动应力比为0.06、0.1、0.2的循环加载试验，得到轴向循环塑性应变与时间的关系，分析得到围压、动应力比及固结形式对轴向循环塑性应变的影响规律；将Abel黏壶引入开尔文模型，得到分数阶开尔文模型；利用遗传算法优化轴向循环塑性累积应变的开尔文模型和分数阶开尔文模型的参数，通过分析两组模型的计算值与试验值的对比曲线，得到分数阶开尔文模型更适合模拟计算循环荷载下饱和软黏土的累积变形。

饱和软黏土；开尔文模型；分数阶开尔文模型；遗传算法

在路基沉降计算中，长期交通荷载引起的软土地基累积沉降占主要部分，因此研究循环荷载作用下饱和软黏土的累积变形具有非常重要的意义。

国内外学者通过大量的室内试验和现场试验，经拟合分析得到描述不同循环累积应变和循环次数之间关系的经验模型。文献[1]在考虑累积塑性应变速率和循环加载次数关系、循环加载动应力大小及应力历史等的影响因素条件下提出了指数模型。文献[2]提出了主要考虑应变与循环次数的指数关系的指数模型，而在此后提出的指数模型多是在此基础上提出的。如文献[3-4]提出的考虑初始静偏应力、静破坏偏应力和动偏应力影响的模型，文献[5-7]等提出的相对偏应力模型。这些由试验拟合得到的经验模型参数没有明确的物理意义，且难以确定。而由整数阶元件组合而成的整数阶模型具有理论性强，物理概念清晰的特点[8]。但从以往的试验和研究得到，在运用整数阶微积分得到的整数阶微积分型本构方程描述岩土的蠕变曲线时，在蠕变或松弛的初始阶段不能与实验数据很好吻合[9-10]。在整数阶微积分模型基础上得到的分数阶微积分模型不仅能体现整数阶微积分模型的优点，而且能改善其不足之处[11]。

本文是将Abel黏壶引入开尔文模型，得到分数阶开尔文模型，用遗传算法优化参数来计算循环三轴轴向循环塑性累积应变。遗传算法是采用二进制遗传编码的一种自适应全局优化搜索算法[12]。通过分析广义开尔文模型和分数阶开尔文模型的计算值与试验值，得到分数阶开尔文模型更能真实的反映循环荷载下饱和软黏土的累积应变特征。

1　循环荷载下饱和软黏土三轴试验

1.1试样制备及方法

试验所用的土样深度为地表以下10～12 m的上海第④ 层淤泥质软黏土。为了尽可能减少对土样的扰动，用挖土机挖至取样深度，将挖土面修平后，把取样筒垂直插入土中，然后把周围土挖掉取出土样。

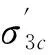
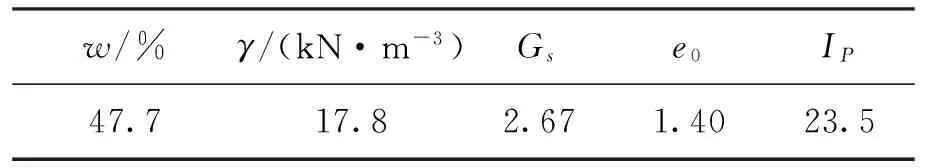
表1　土样物理指标

1.2试验结果及分析

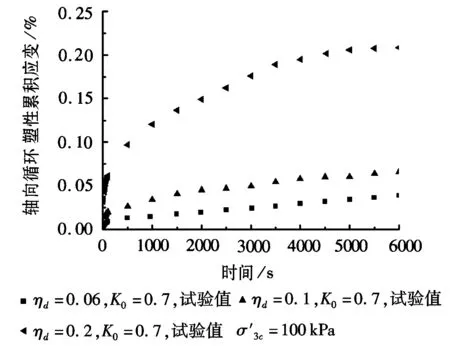
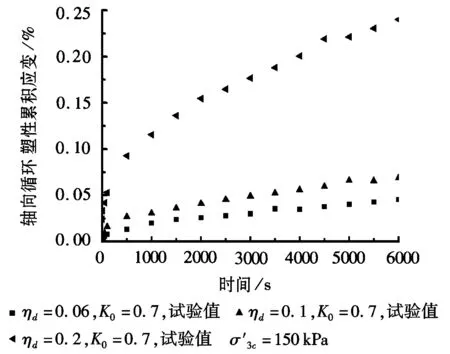
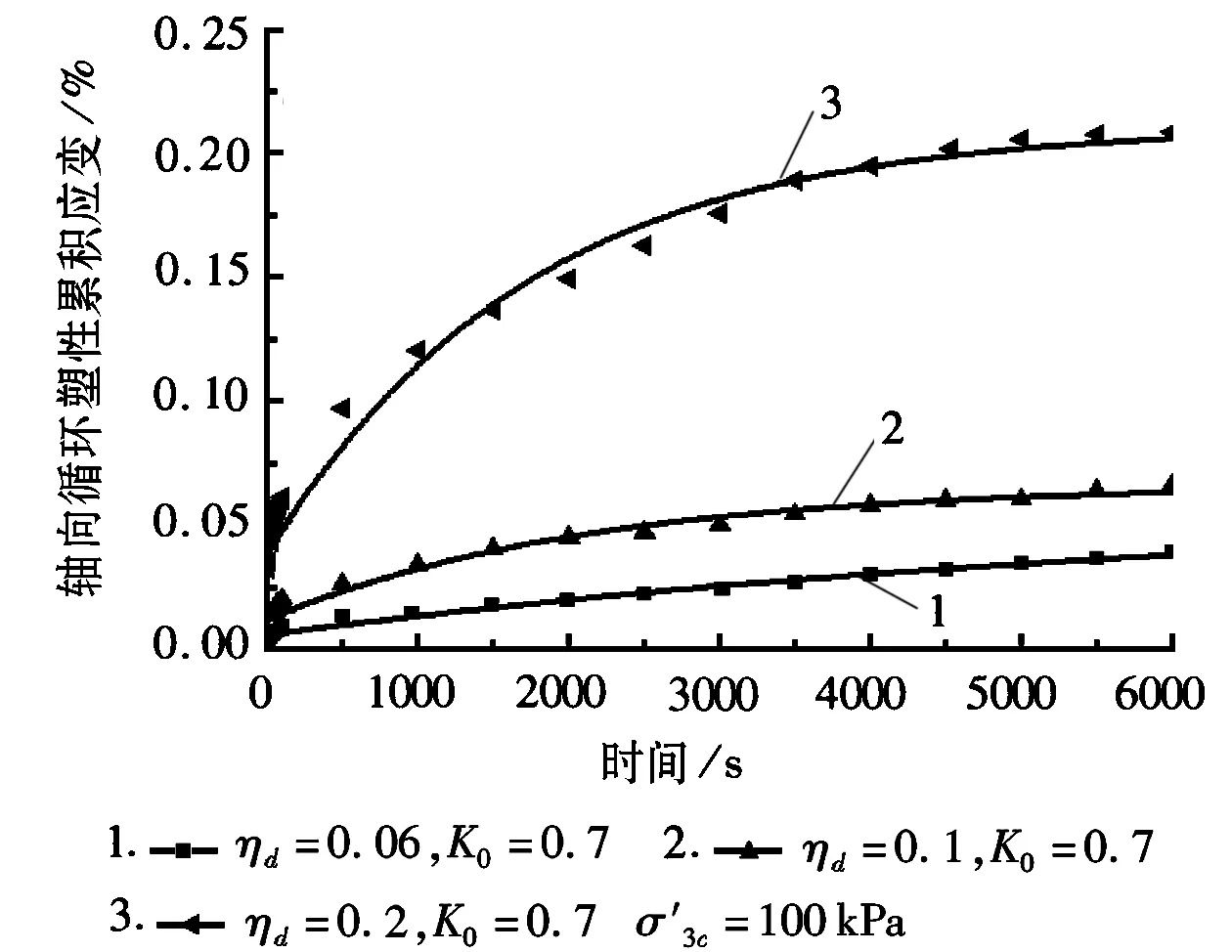
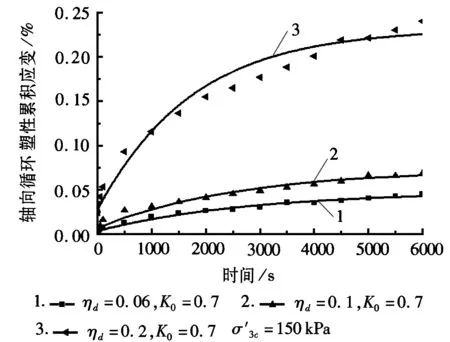
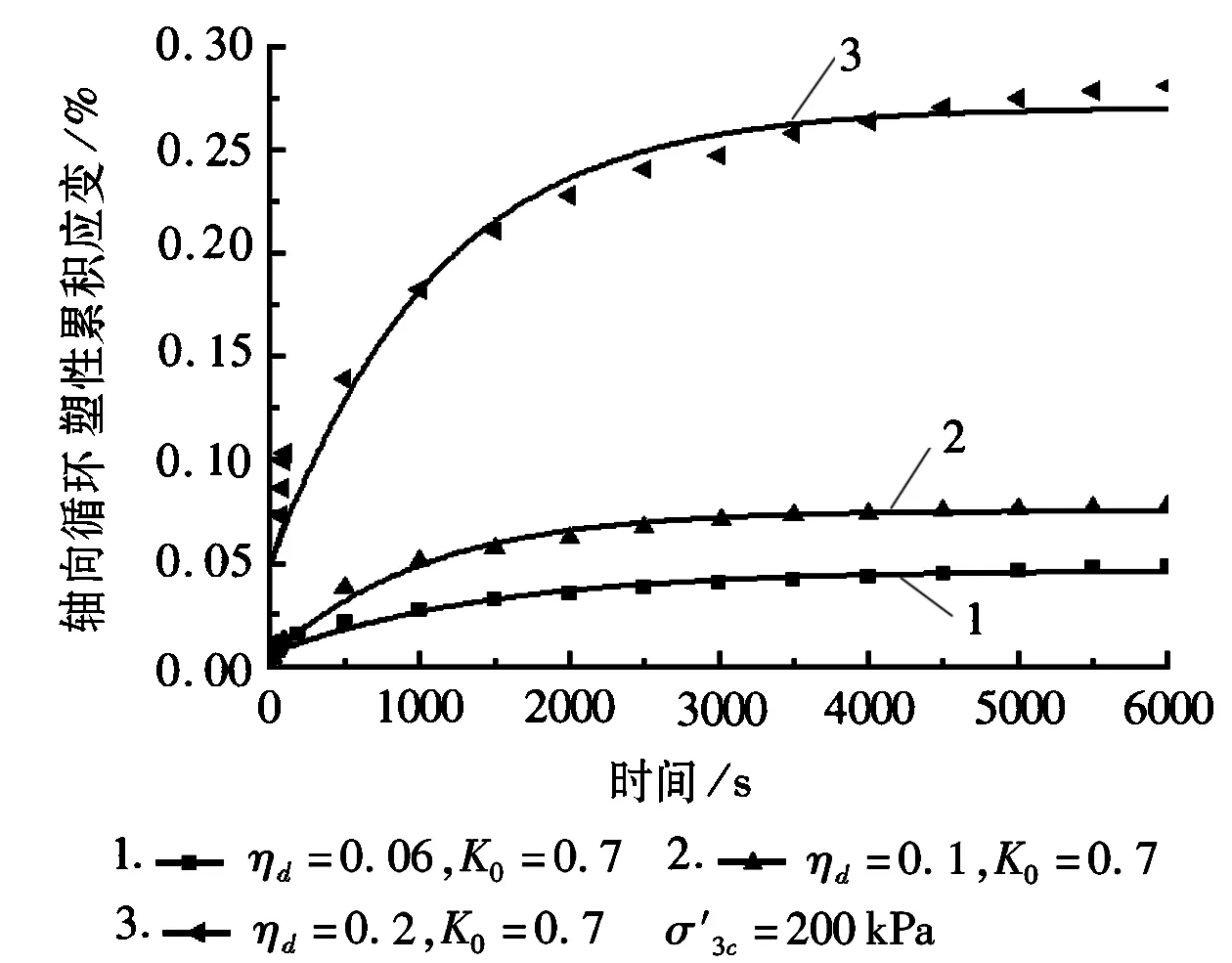
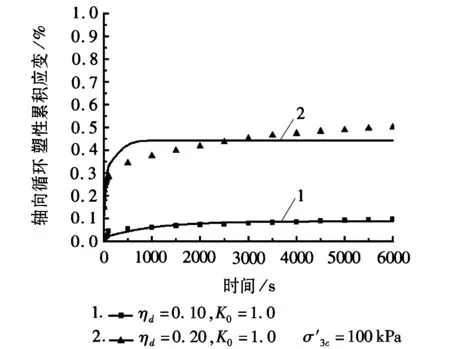
偏压固结条件下循环三轴轴向循环塑性累积应变与循环时间的关系如图1所示，等向固结条件下循环三轴轴向循环塑性累积应变与循环时间的关系如图2所示。

a

b

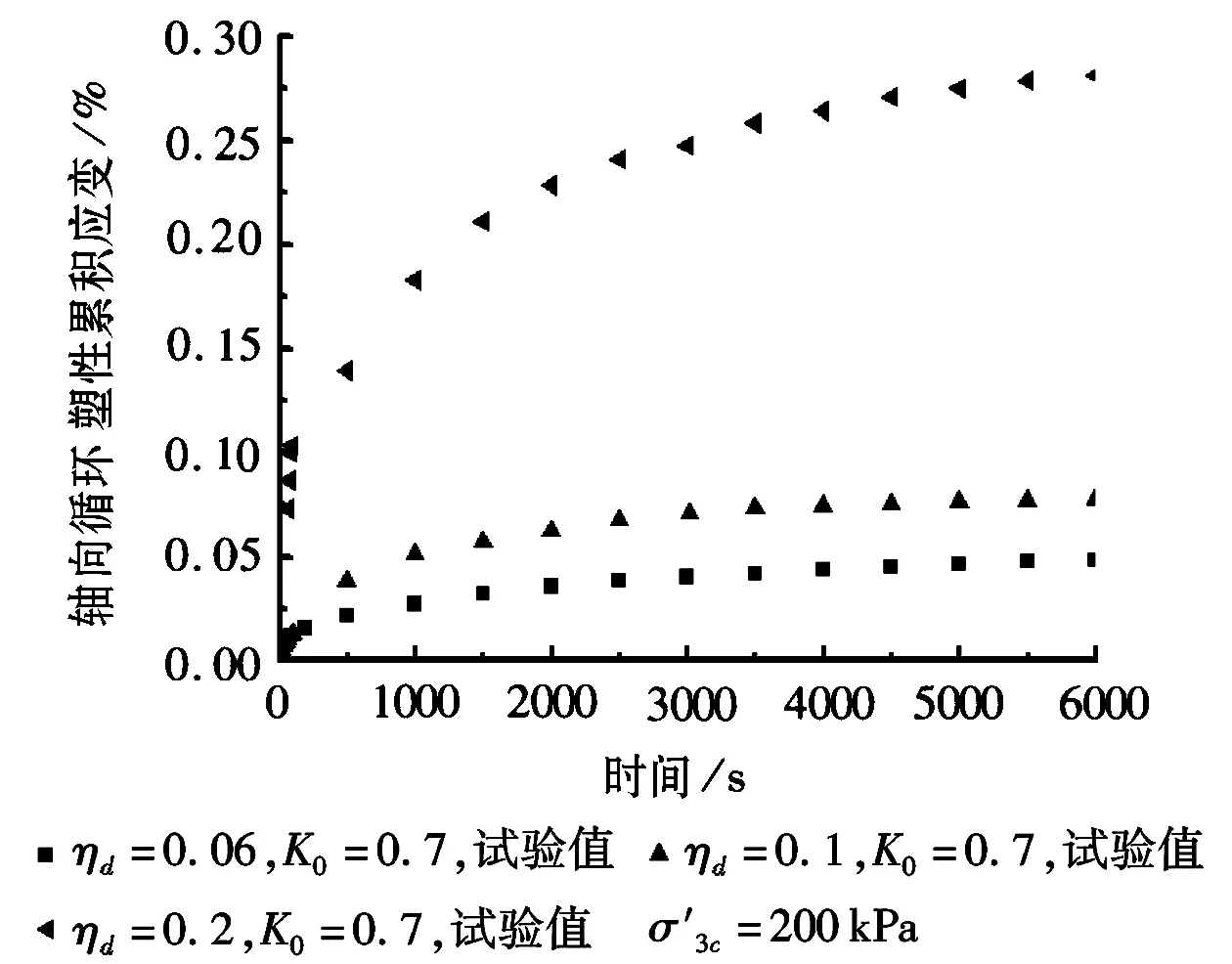
c图1　偏压固结条件

从图1可以得出，随着循环时间的增加，轴向循环塑性累积应变逐渐增加，最后逐渐趋于一个稳定值。对比图1中的曲线得到，当围压相同时，动应力比大的，对应的达到的稳定累积应变值也大，可见动应力比对轴向循环塑性累积应变影响显著。

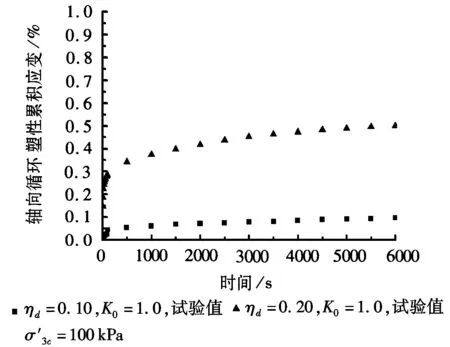
a

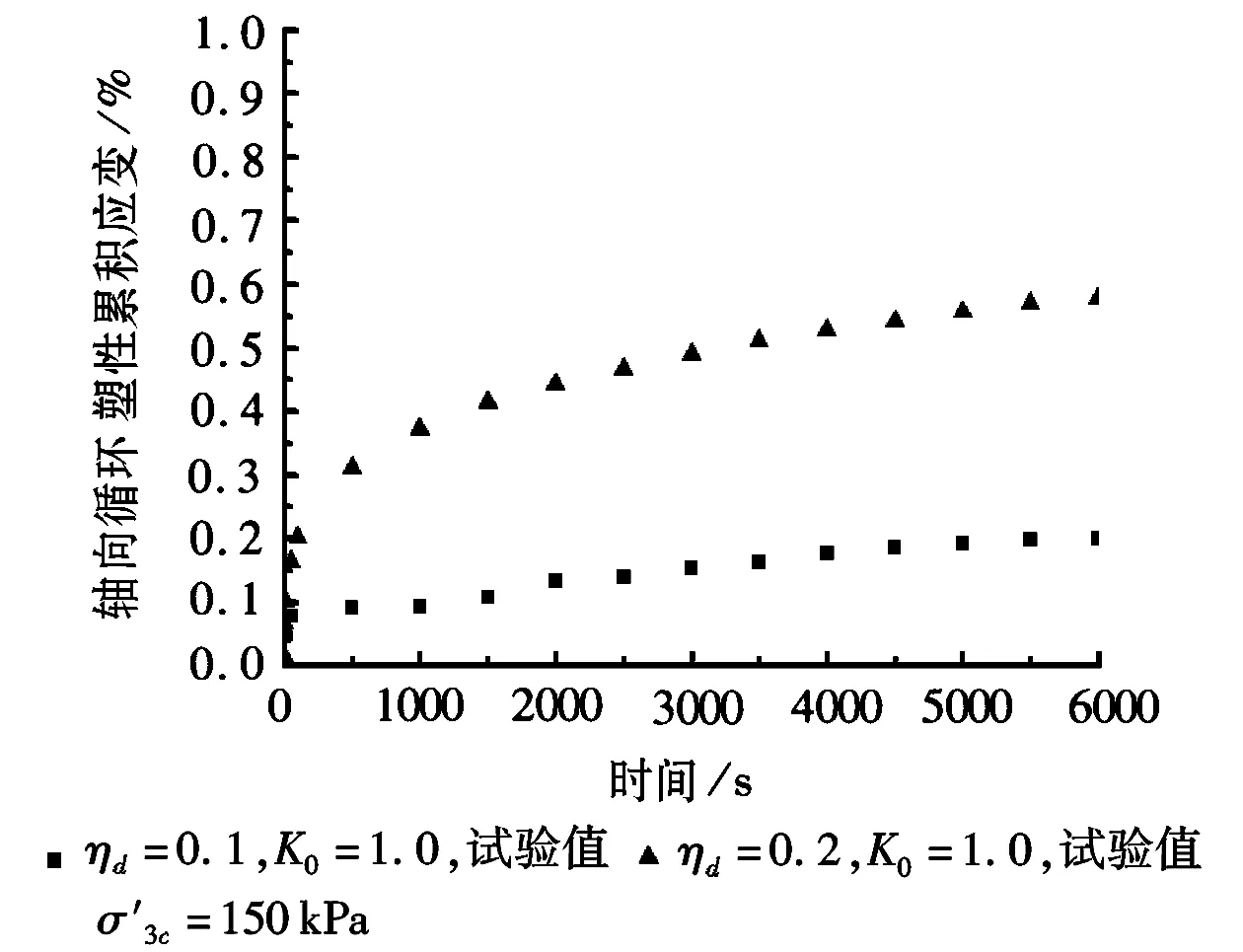
b

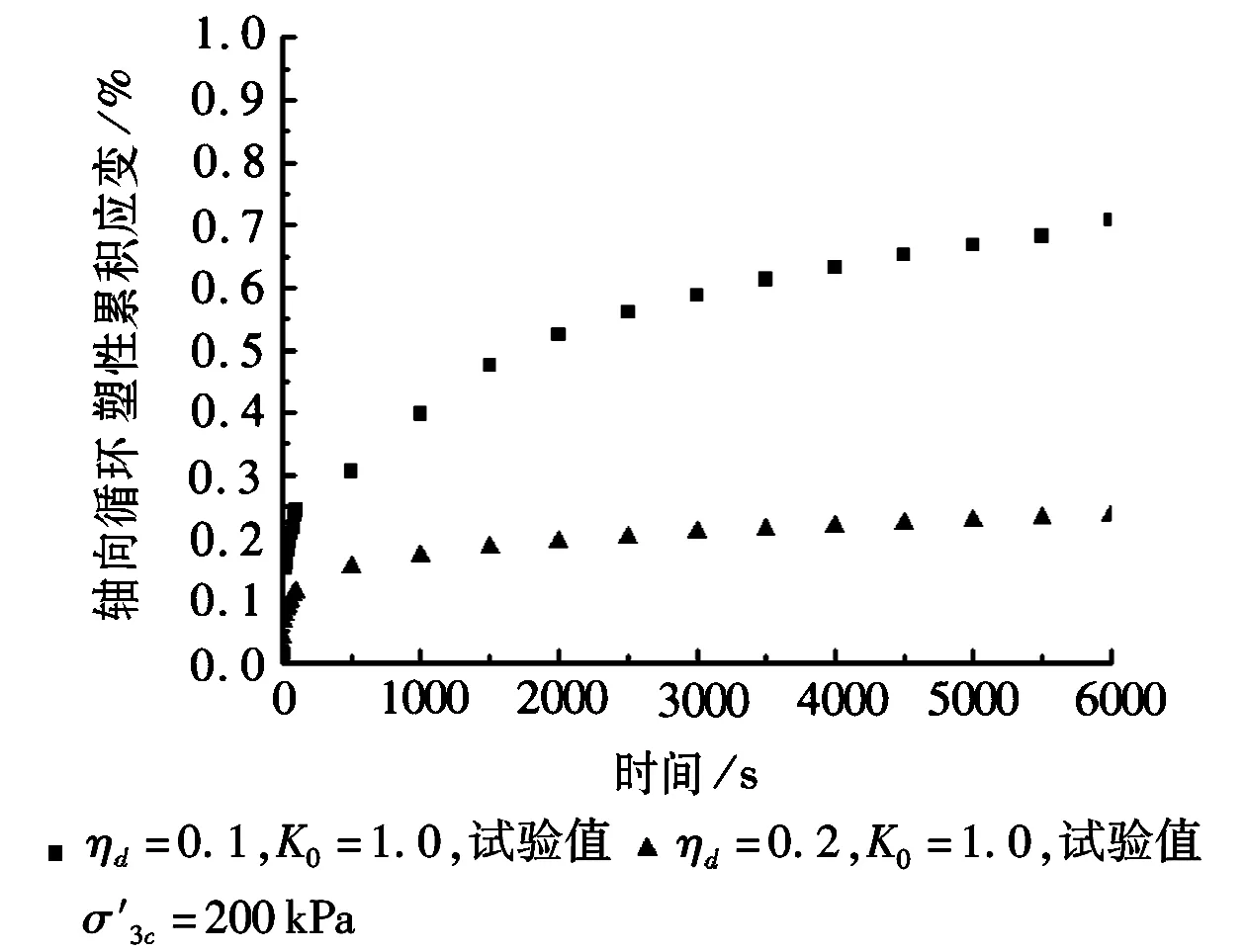
c图2　等向固结条件

从图2中得出在等向固结条件下，轴向累积应变也是随循环时间的增加逐渐增加最后趋向一个稳定值。但对比图1、图2可以得到，当围压和动应力比相同时，等向固结条件下的轴向累积应变要大于偏压固结条件下的轴向累积应变，可见固结形式对轴向循环累积应变的影响也较显著。

2　分数阶导数模型

2.1广义Kelvin模型

广义Kelvin模型元件是由一个开尔文元件和一个牛顿体串联而成(见图3)。

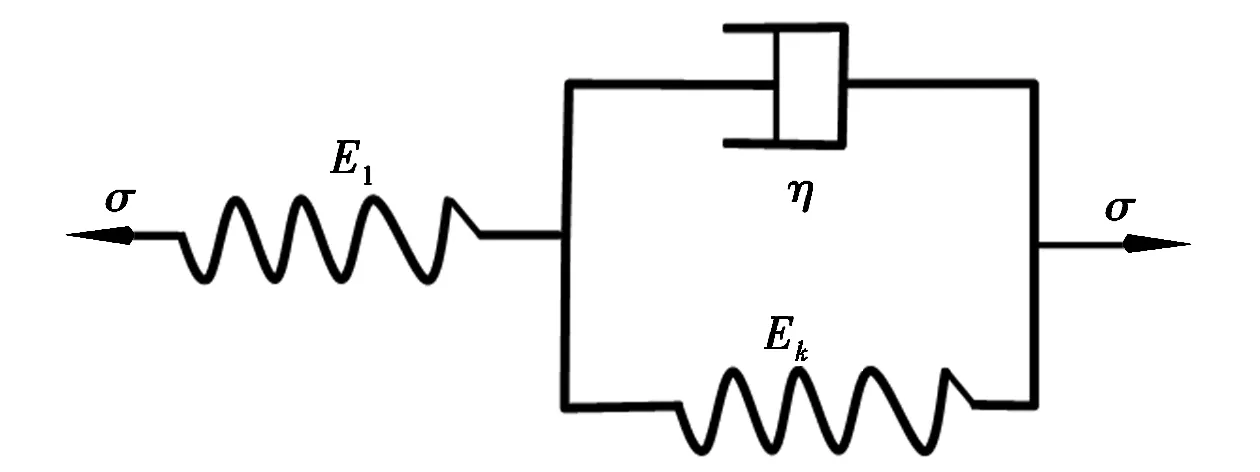
图3　广义Kelvin模型

其本构方程为

(1)

式中：E1，Ek均表示广义Kelvin体中材料的弹性参数，η表示黏壶的黏滞系数；t表示时间。

2.2分数阶导数开尔文模型

采用分数阶导数的流变模型理论实质上就是用Abel黏壶取代经典模型理论中的Newton黏壶，分数阶导数开尔文模型组成如图4所示。

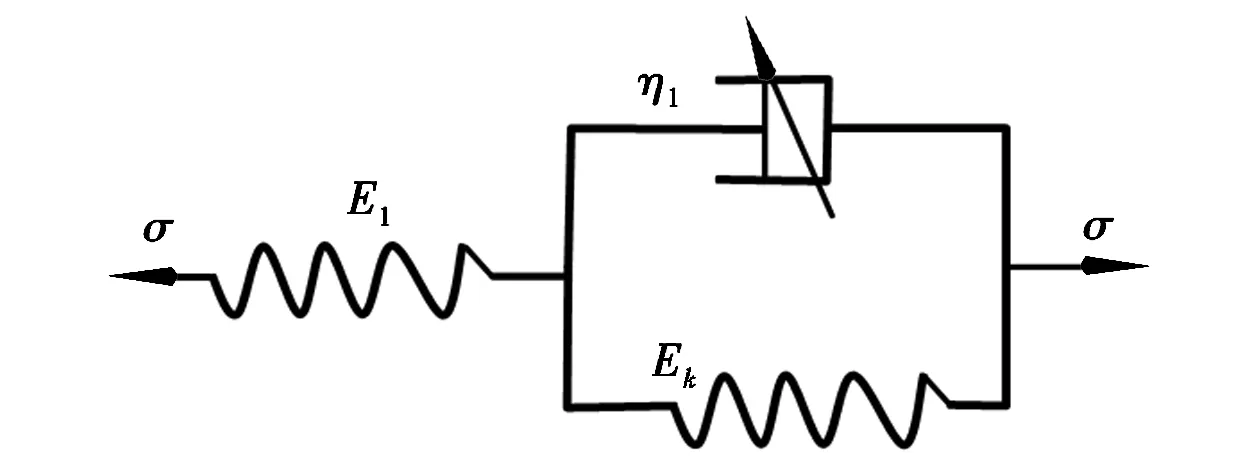
图4　分数阶导数开尔文模型

运用Riemann-Liouville分数阶微分算子理论，对函数f(x)的r阶微分定义为[13]

(2)

式中：Dr表示分数阶微分算子，r取值区间为(0，1)，Γ是Gamma函数。

(3)

定义Abel黏壶体的本构关系是应力与应变的分数阶导数成正比。则它的本构关系为

σ=ηDrε(t)(0≤r≤1)

(4)

则根据Riemann-Liouville分数阶微积分算子理论，可得

(5)

可得分数阶导数开尔文模型的本构方程为

(6)

2.3遗传算法优化模型参数

遗传算法(Genetic Algorithm， GA)是一种基于自然群体遗传演化原理而建立的一种最优化的高效探索算法，它是美国Michigan大学Holland教授于1975年首先提出来的[14-15]。遗传算法是用于解决最佳化的搜索算法，是进化算法的一种。在遗传算法中，它将问题域中的每个可能解看作是群体的一个个体或者是染色体，对群体的每个个体按照它们对环境适应度施加一定的操作(遗传，交叉和变异)，依据适者生存，优胜劣汰的进化规则，用全局并行搜索方式进行搜索优化，进而求得满足要求的最优解。

遗传算法的步骤[16]：

1) 先定义目标函数f(x)；

4) 按照优胜劣汰原则淘汰适应值差的染色体，将剩余的染色体按一定的概率进行随机选择，形成新的群体，选择的概率公式为

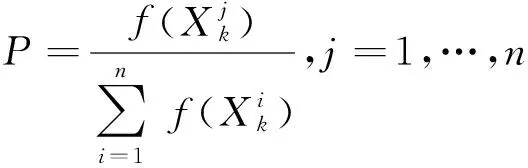
5) 对新的群体进行杂交、变异，产生子代。杂交是在新的群体中以等概率选择两条染色体(双亲)，将这两个个体按照预设的概率P1杂交产生两个新个体，变异是对新群体的每个个体基因中的某一点或多点以一定的概率P2进行随机改变；

6) 测试是否达到迭代收敛(适应值趋稳定)，否则重复步骤(3)～(5)的操作，直到满足条件，即得到最优解(准最优解)。

2.4饱和软黏土累积变形分数阶模型

1) 广义开尔文模型。利用遗传算法优化广义开尔文模型参数，模型参数见表2。广义开尔文模型的计算值与循环荷载下饱和软黏土三轴试验试验值对比如图5～图6所示。

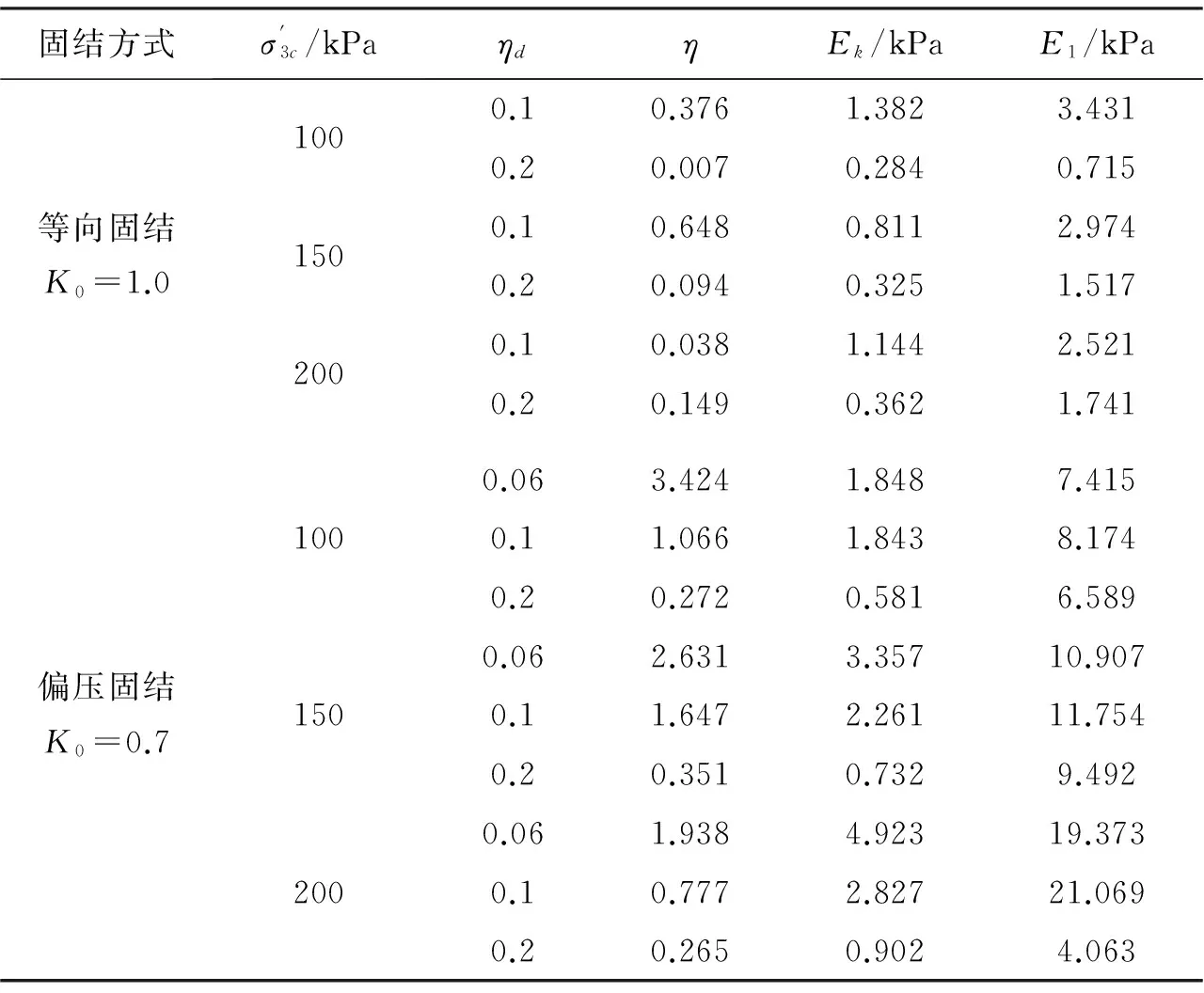
表2　广义开尔文模型参数

a

b

c图5　广义开尔文模型计算值与偏压固结试验值

a

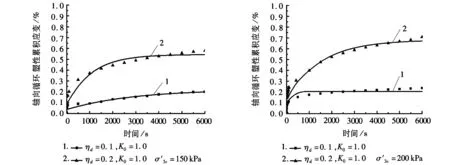
b c图6　广义开尔文模型计算值与等向固结试验值

对比图5、图6中广义开尔文模型的计算值与试验值得到：当动应力比较小时，模拟曲线与试验得到的曲线吻合很好，但动应力比较大时，在稳定阶段吻合较好，但是在加速阶段误差较大。因此可见，广义的开尔文模型计算轴向循环塑性累积变形的误差较大。

2) 分数阶导数开尔文模型。利用遗传算法优化分数阶导数开尔文模型的参数，模型参数见表3。分数阶导数开尔文模型的计算值结果如图7-8所示。

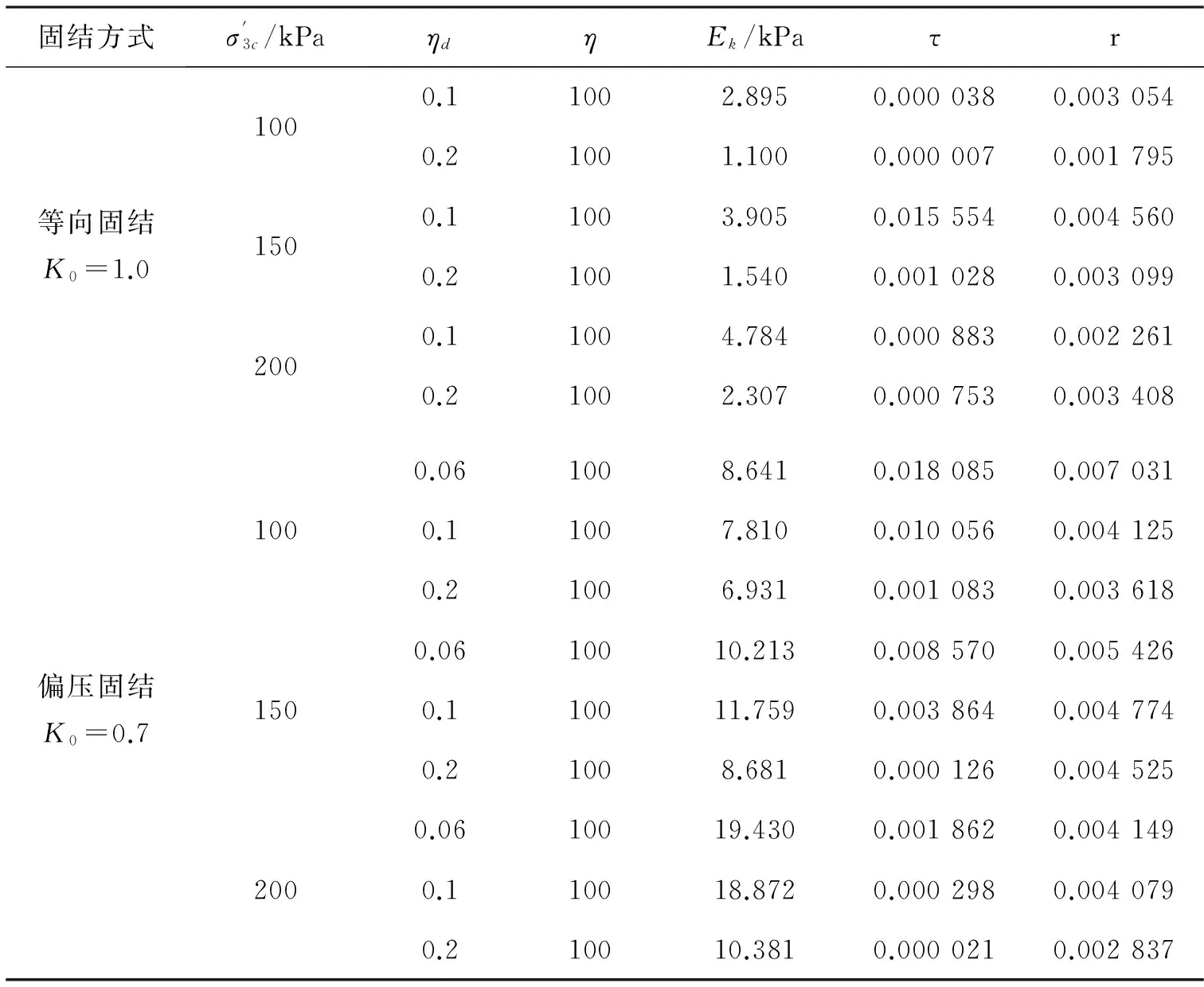
表3　分数阶导数开尔文模型参数

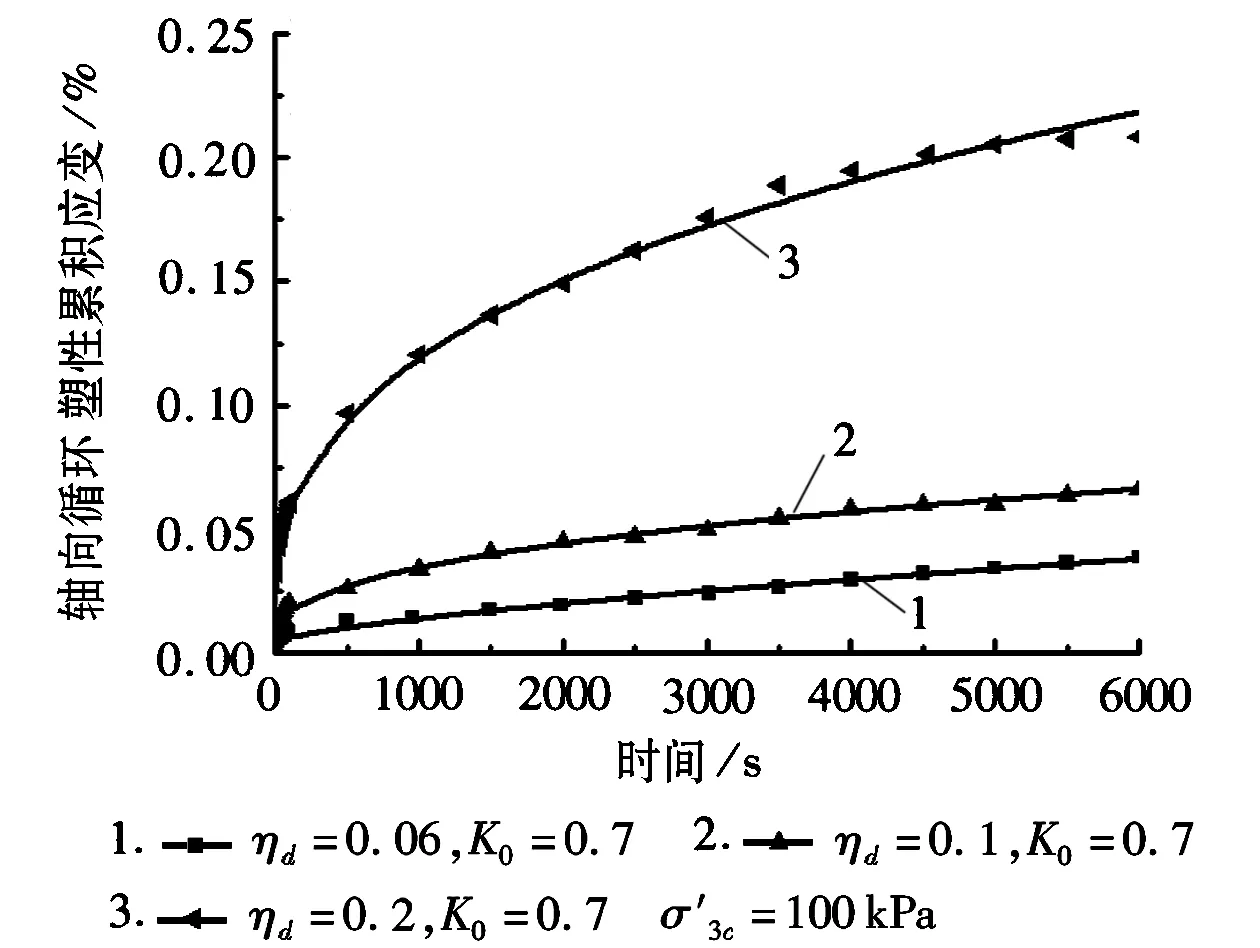
a

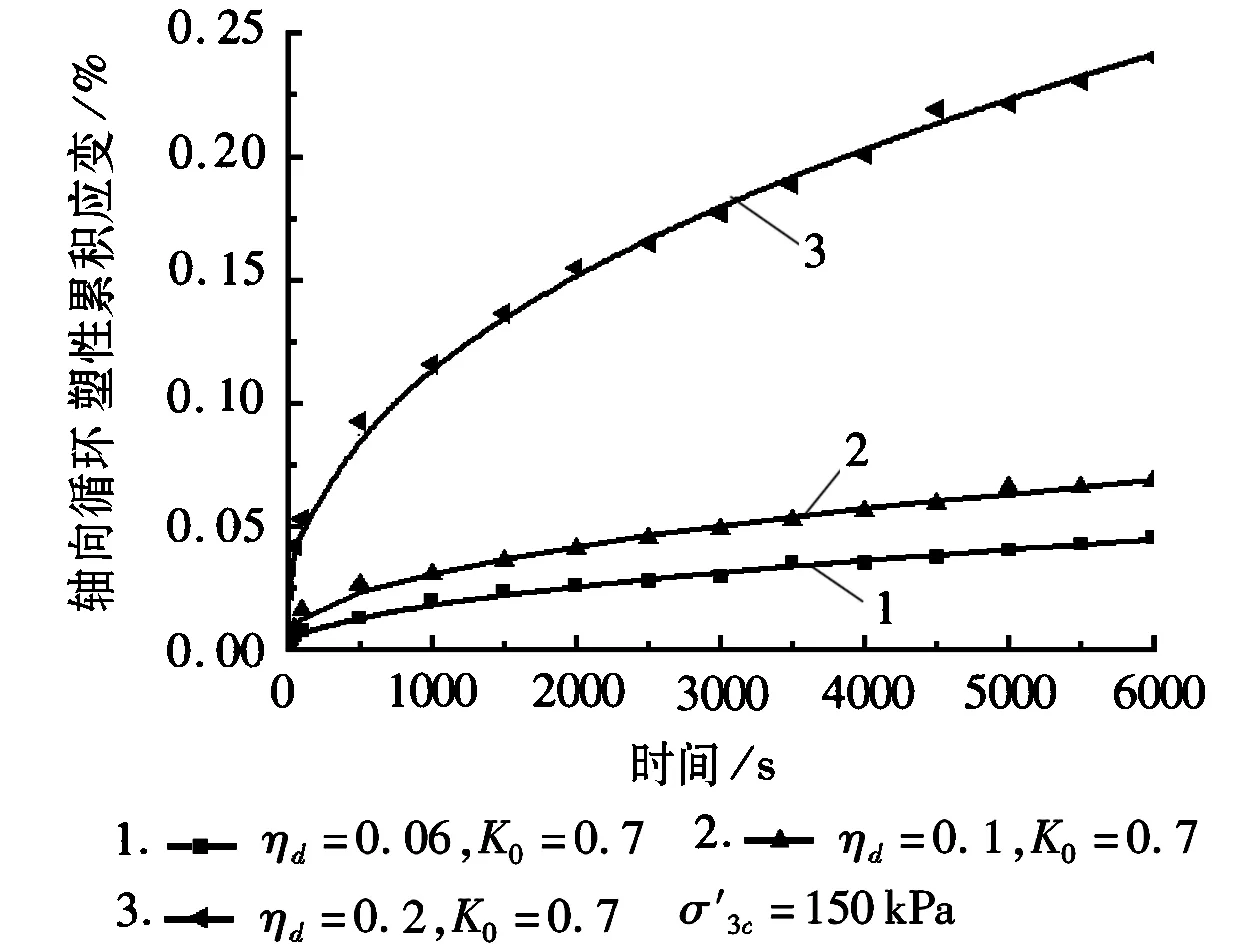
b

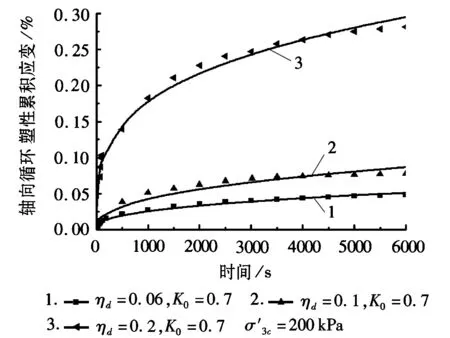
c图7　计算值与偏压固结试验值

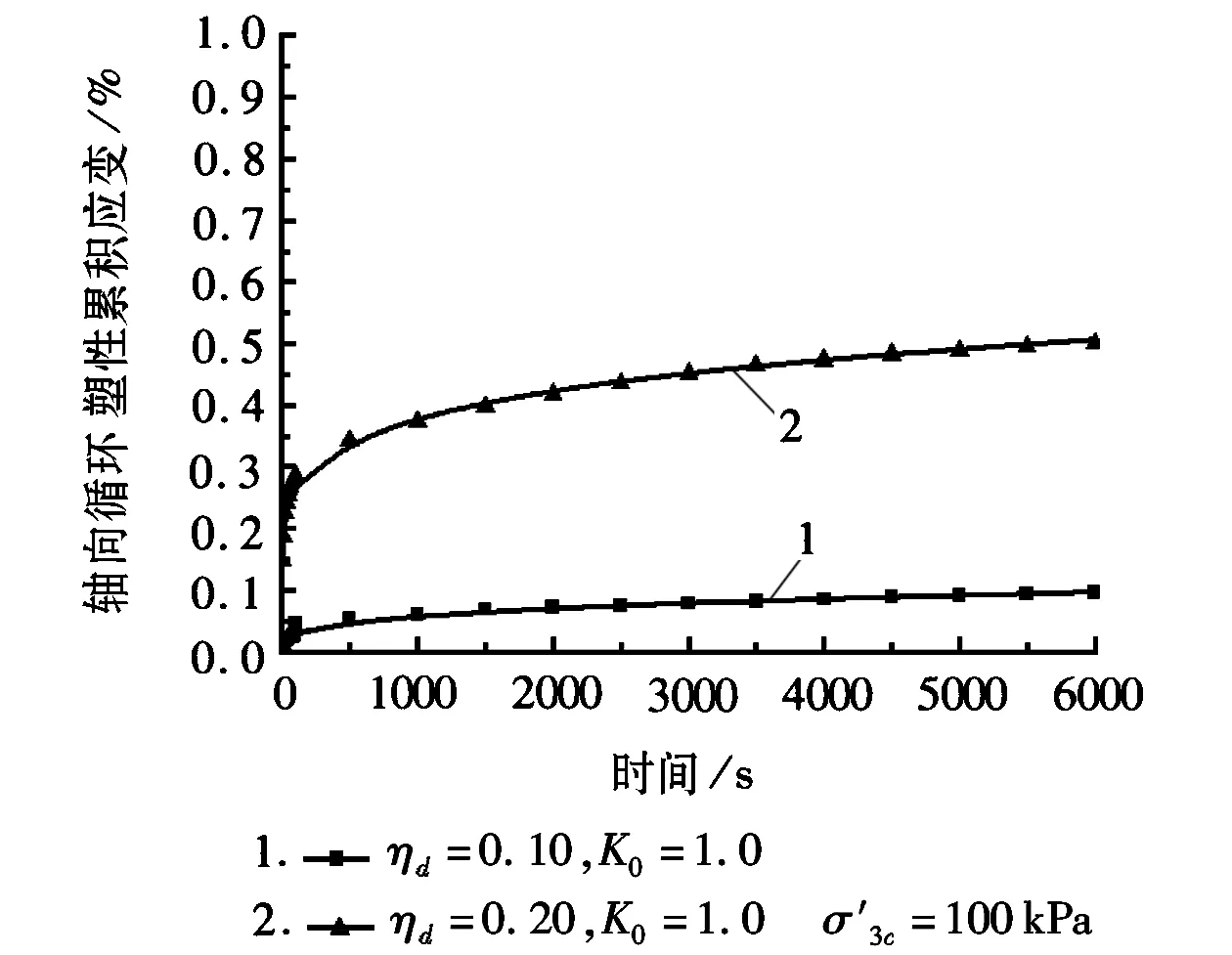
a

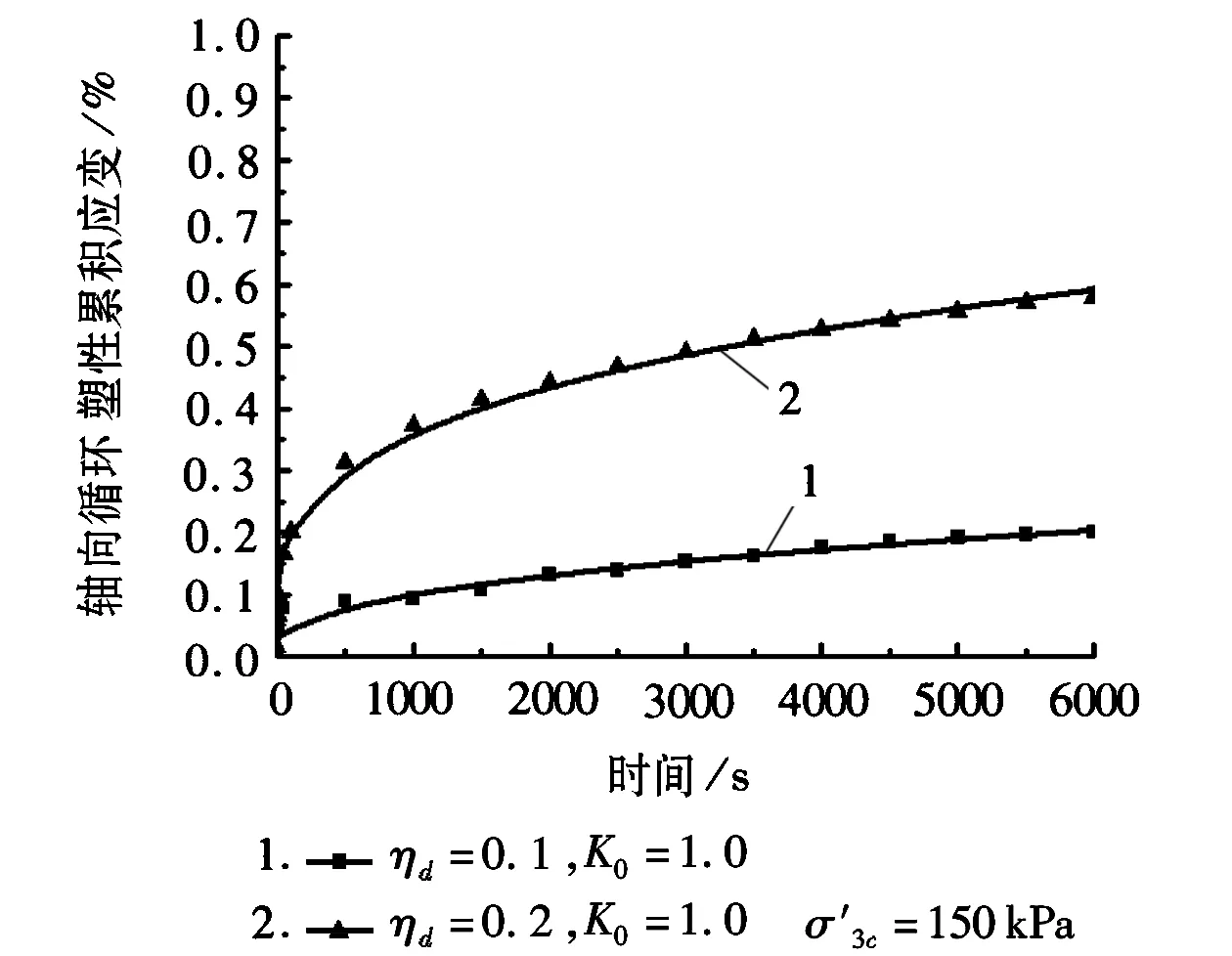
b

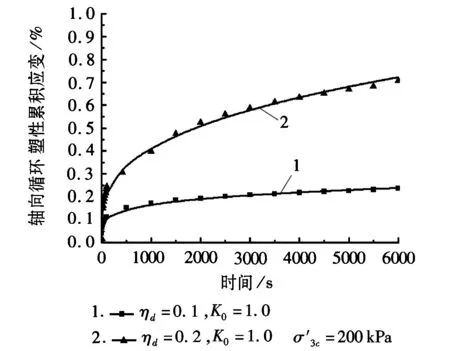
c图8　计算值与等向固结试验值

分析图7、图8可以得到，经遗传算法优化的分数阶开尔文模型的模拟曲线与试验值吻合很好，则可得出分数阶开尔文模型能很好地计算饱和软黏土轴向循环塑性累积变形。

3　结论

1) 随着循环时间的增加，轴向循环塑性累积应变逐渐增加，最后逐渐趋于一个稳定值。

2) 当围压相同时，动应力比大的，对应达到的稳定的累积应变值也大，可见动应力比对轴向循环塑性累积应变影响显著。当围压相同时，相同的动应力比条件下，等向固结条件下的轴向循环塑性累积应变明显大于偏压固结条件下的轴向循环塑性累积应变，由此可见固结形式对轴向循环塑性累积应变影响较大。

3) 遗传算法能有效优化分数阶开尔文模型参数；分数阶开尔文模型能很好地计算饱和软黏土轴向塑性累积变形。

[1]PARR G B. Some aspects of the behaviour of London clay under repeated loading[D]. UK： University of Nottingham， 1972.

[2]MONISMITH C L， OGAWA N， FREEME C R. Permanent deformation characteristics of subgrade soils due to repeated loading[J]. Transportation Research Board. Washington， D. C.， 1975：1-17.

[3]LI D， SELIG E T. Cumulative plastic deformation for fine-grained subgrade soils[J]. Journal of Geotechnical Engineering. 1996，122(12)：1 006-1 013.

[4]CHAI J C， MIURA N. Traffic-load induced permanent deformation of road on soft subsoil[J]. Journal of Geotechnical and Geoenvironmental Engineering，2002，128(11)： 907-916.

[5]黄茂松，李进军，李兴照.饱和软粘土的不排水循环累积变形特性[J].岩土工程学报，2006，28(7)：891-895.

[6]刘明，黄茂松，柳艳华.车振荷载引起的软土越江隧道长期沉降分析[J].岩土工程学报， 2009， 31(11)：1 703-1 709.

[7]黄茂松，姚兆明.循环荷载下饱和软黏土的累积变形显式模型[J].岩土工程学报，2011，33(3)：325-331.

[8]齐亚静，姜清辉，王志俭，等.改进西原模型的三维蠕变本构方程及其参数辨识[J].岩石力学与工程学报，2012， 31(2)： 347-355.

[9]康永刚，张秀娥.岩石蠕变的非定常分数伯格斯模型[J].岩土力学，2011，32(11)：3 237-3 241.

[10]姚兆明，周洋，徐颖，等.人工冻土遗传分数阶导数加速伯格斯蠕变模型[J].工业建筑，2013，43(11)：73-76.

[11]殷德顺，和成亮，陈文.岩土应变硬化指数理论及其分数阶微积分理论基础[J].岩土工程学报，2010，32(5)：762-766.

[12]葛继科，邱玉辉，吴春明，等.遗传算法研究综述[J].计算机应用研究，2008，25(10)：2 911-2 915.

[13]孙海忠， 张卫. 一种分析软土黏弹性的分数阶导数开尔文模型[J].岩土力学， 2007， 28(9)：1 983-1 986.

[14]乔均俭，付君丽，徐雅玲.应用遗传算法原理确定函数的最优解[J].微计算机信息杂志，2007，23(18)：240-241.

[15]王志美，陈传仁.遗传算法理论及其应用发展[J].内蒙古石油化工，2006(9)：44-45.

[16]赵越，茹婷婷.遗传算法理论与应用新探[J].计算机与信息技术，2014(1)：77-78.

(责任编辑：李丽,吴晓红)

Genetic Algorithm Fractional Order Derivative Kelvin Model for Cumulative Strain of Saturated Soft Clay under Cyclic Loading

ZHANG Qiu-jin, YAO Zhao-ming, JIANG Zi-hua, WANG Chun-meng

(School of Civil Engineering and Architecture, Anhui University of Science and Technology,Huainan Anhui 232001, China)

To study the accumulative deformation of saturated soft clay under cyclic load has practical significance for foundation settlement calculation caused by the traffic load. The cyclic loading tests of the isotropic dynamic stress ratio of 0.2, 0.1 and the anisotropic consolidation dynamic stress ratio of 0.06, 0.1, 0.2 are conducted for saturated soft clay, whose confining pressure is respectively 100kPa,150kPa and 200kPa.The relationship of axial cyclic plastic strain with time as well as the influencing rule of confining pressure, dynamic stress and consolidation form to axial cyclic plastic strain are gained. The Abel dashpot is introduced into the Kelvin model, and the fractional order derivative Kelvin model is established. The parameters of Kelvin model and fractional order derivative Kelvin model of axial plastic cumulative strain are optimized by genetic algorithm. By analyzing the correlation curve of calculation value and trial value of two models, the fractional order derivative Kelvin model is more appropriate for calculating cumulative strain of saturated soft clay under cyclic loading.

saturated soft clay; Kelvin model; fractional order derivative Kelvin model; genetic algorithm

2015-08-25

张秋瑾(1991-)，女，河南南阳人，在读硕士，研究方向：岩土工程。

TU473

A

1672-1098(2016)04-0052-08