面向差分调制解调的编码码率研究

徐亚冲，胡东伟

（中国电子科技集团公司第五十四研究所，河北 石家庄 050081）

面向差分调制解调的编码码率研究

徐亚冲，胡东伟

（中国电子科技集团公司第五十四研究所，河北 石家庄 050081）

差分调制解调是解决无线通信高动态条件下信息传输的一种重要方法。针对面向差分调制解调的编码码率既不宜过高，也不宜过低的问题，从信息论的角度，分别针对差分BPSK调制和差分QPSK调制，分析了各种不同码率下无差错传输的香农限，得出了最佳的编码码率。通过采用不同码率的卷积编码和Turbo编码，实验仿真验证了所得理论的正确性。

差分调制解调；编码码率；卷积编码；Turbo编码

1 引言

差分调制解调是解决无线通信高动态条件下信息传输的一种重要方法。 在无线通信中，物体在高速移动中会产生多普勒频移。地面移动通信的高动态还会带来小区切换的问题。卫星移动通信的高动态还会带来跟踪和同步的问题。差分调制解调是高动态条件下信息传输的一种重要方法，也是目前克服高动态效应很有效的方法。其他信息传输方法，如多进制扩频、采用并行导频等，在能够克服的高动态范围方面，均不如差分调制解调，也不能比差分调制解调更节省比特能量［1～3］。因此，差分调制解调可以在保证可靠性的基础上，比其他方法更为高效地进行信息传输。

面向差分调制解调的编码问题是一个有趣的问题。当编码码率太高时，根据香农定理，它不能有效利用带宽，不能达到最有效地利用比特能量［4］；当编码码率过低时，比特能量分散到各个编码码元，码元能量过低，导致接收端接收信号信噪比太低，差分解调时，噪声得到极大的放大，这会导致译码时发生更多的错误。因此，直观上判断，面向差分调制解调的编码码率，既不宜过高，不宜过低。那么，究竟采取哪种编码码率才能达到性能最优？直至目前，尚未见文献对这一问题进行研究。本文试图从信息论的角度，计算不同码率下的香农限［5，6］，寻找出面向差分调制解调的最优的编码码率。

2 信号模型

设发送信号为s（n），接收信号为r（n），则

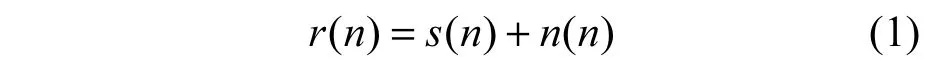
其中，n（n）为高斯白噪声。n（n）的均值为0，方差记为。则

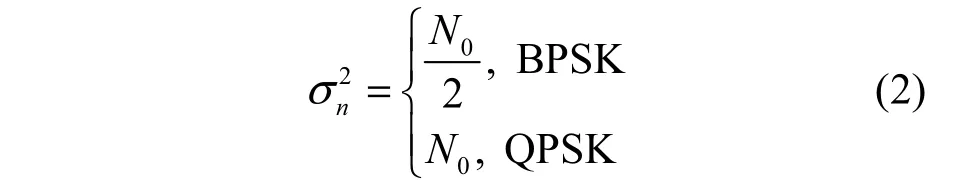
其中，0N为自然噪声的单边带功率谱密度。

对接收信号进行差分解调，有

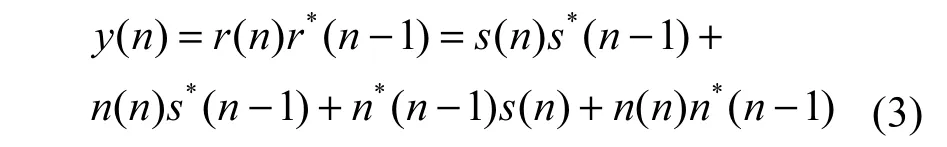
其中，（·）*表示复共轭。式（3）中第一项为信号项，其他3项为噪声项。记

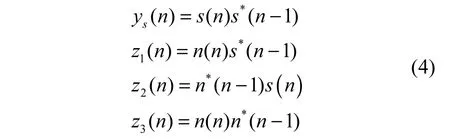
显然，由于噪声为高斯白噪声，z1（n）、z2（n）、z3（n）相互独立，且z1（n）、z2（n）符合高斯分布。z1（n）、z2（n）的均值均为0，方差均为Es。其中

为发送的符号能量。E｛·｝为求期望值。记

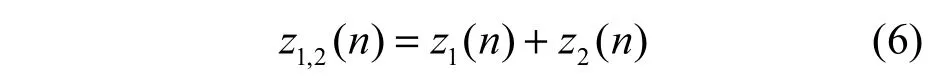
则z1，2（n）均值均为0，方差为，且符合高斯分布。

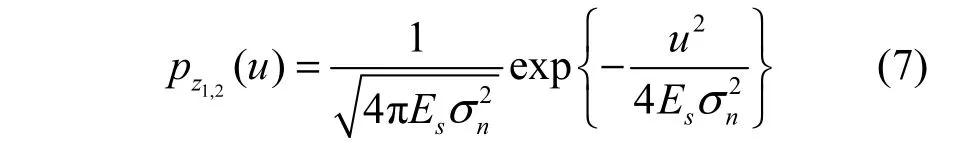
z3（n）的均值为0，方差为

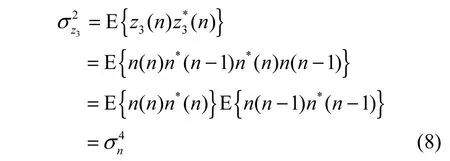
z3（n）为2个独立高斯随机变量的乘积，其概率密度函数为［7］

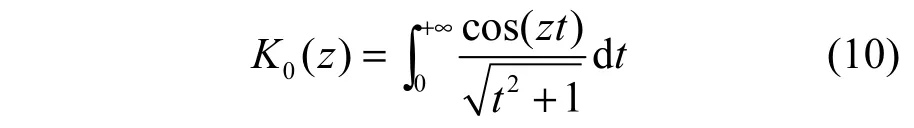
当0z=时，

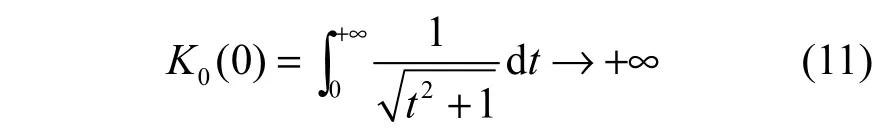
图1给出了z3（n）的概率密度函数。其中，取1。为方便比较，图中同时画出了标准方差的高斯函数。

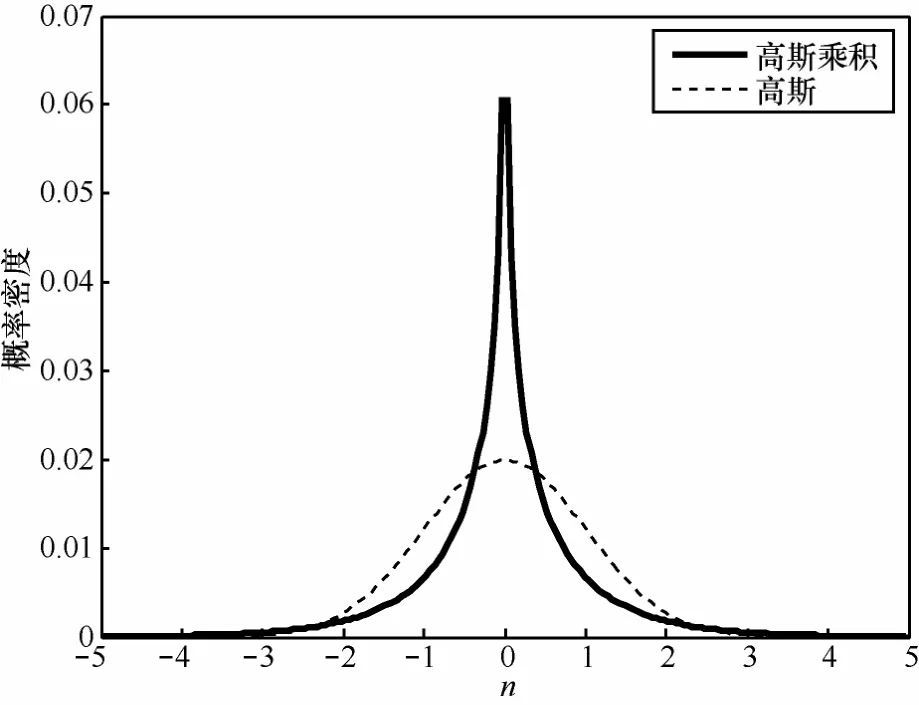
图1 z3（n）（2个高斯随机变量乘积）的概率密度函数

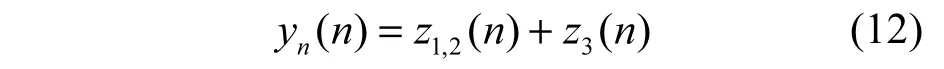
由于z1，2（n）和z3（n）独立，yn（n）的概率密度函数为z1，2（n）和z3（n）概率密度函数的卷积［8］

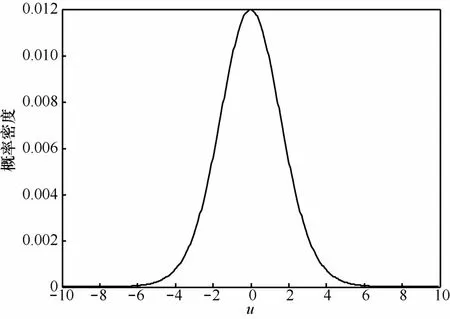
图2 噪声项yn（n）的概率密度函数

根据以上推导，差分检测后的信号y（n）可记为

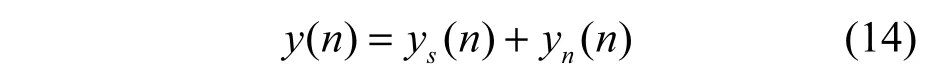
其中，ys（n）为信号项，yn（n）为噪声项。

3 香农限的计算

从发送s（n）到接收y（n），信道传递的互信息为

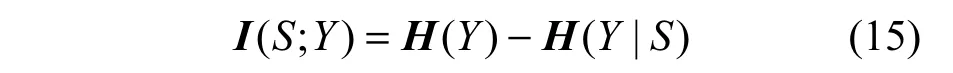
其中，H（·）为信源熵，如下

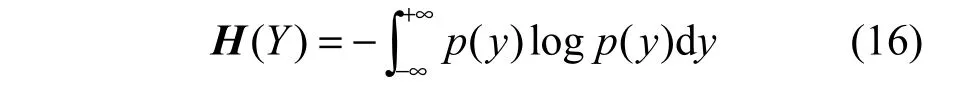
根据香农定理，信道容量为最大互信息［4］

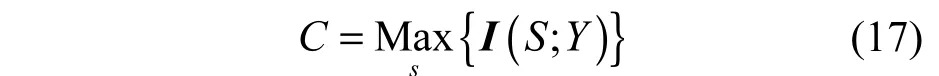
显然，信道容量C跟调制方式有关，且为信号能量Es和噪声功率的函数。下面的推导中，限定Es=1。于是，对于码率为R的编码，比特能量Eb为

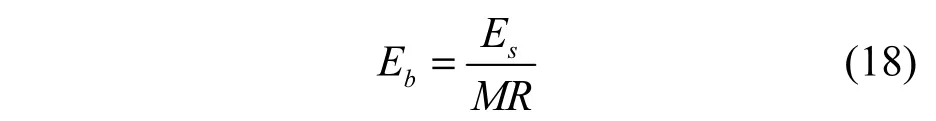
其中，M为调制阶数。对于差分BPSK调制，M=1；对于差分QPSK调制，M=2。

香农限是指达到信道容量的无误码传输时，所需要的最小比特能量，通常用来表示。下面分别计算差分BPSK调制和差分QPSK调制的香农限。

3.1 差分BPSK调制的香农限

对于差分检测所得的信号y（n），其概率密度函数为［5］

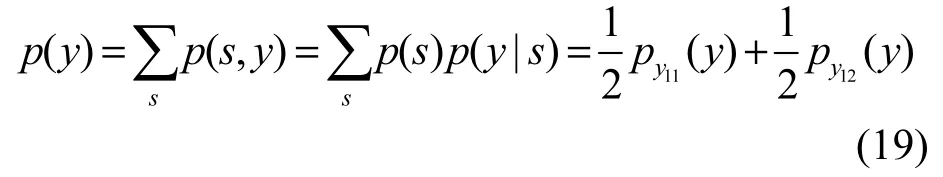
其中，py11（y）为pyn（u）左移到以-1为中心，py12（y）为pyn（u）右移到以+1为中心。因此，已知pyn（u）时，很容易求得p（y），进而求得H（Y）。由于pyn（u）无法用解析解的形式表达出来，因此需采用数值计算的方式来求取H（Y）。

当y（n）中信号项ys（n）已知时，y（n）的熵和噪声yn（n）的熵相同，即

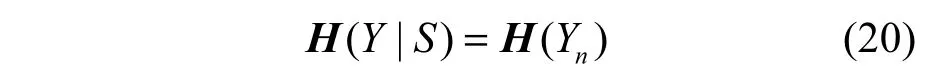
因此，已知pyn（u）时，很容易求得H（Yn），即H（Y|S）。同样，H（Y|S）的求取需采用数值计算的方法。

1） 根据式（7）和式（9）计算pz1，2（u）和pz3（u），其中，Es=1，并注意避开pz3（0）。

2） 根据式（13）计算pyn（u）。

3） 根据式（16）、式（20）计算H（Y|S）。

4） 将pyn（u）分别左移-1和右移+1，得到py11（y）和py12（y）。

5） 根据式（19）得到p（y）。

6） 根据式（16）求得H（Y）。

7） 根据C=H（Y）-H（Y|S）求得信道容量C。

根据以上计算过程，很容易计算出不同噪声方差下的信道容量C，并画出信道容量C和噪声方差之间的变化曲线。再根据式（18）和式（2）的关系，很容易将横坐标2nσ转换为。图3为码率为时信道容量C和的关系。

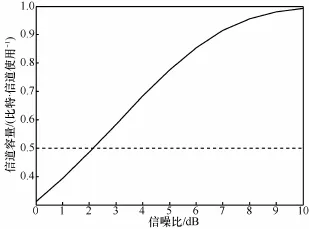
图3码率差分BPSK调制时不同信噪比下的信道容量

根据此方法，可求出不同码率下的香农限。如表1和图4所示。

表1 差分BPSK调制时不同码率下的香农限

图4 差分BPSK调制时不同码率下的香农限

3.2 差分QPSK调制的香农限

计算差分QPSK香农限的过程与计算差分BPSK香农限的过程类似，只不过噪声变为复噪声，实部虚部的分布分别如式（13）所示，且实部虚部独立。同时，式（19）变化为

其中，py21（y）、py22（y）、py23（y）、py24（y）分别为复噪声平移到以1、、exp（jπ）和为中心。

按照求差分BPSK相同的方法，可以求得差分QPSK调制时不同码率下的香农限。图5为码率为时的信道容量，表2和图6为差分QPSK调制时不同码率下的香农限。

图5码率差分QPSK调制时不同信噪比下的信道容量

表2 差分QPSK调制时不同码率下的香农限

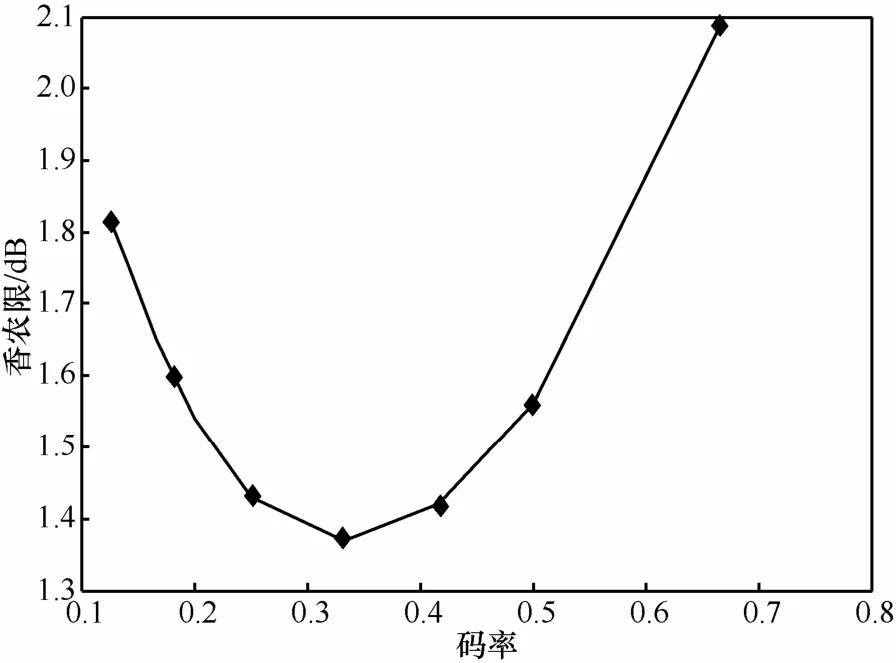
图6 差分QPSK调制时不同码率下的香农限

4 仿真实验

本节采用实际的编码来检验不同码率下差分调制解调的性能。

4.1 不同码率咬尾卷积编码的差分调制解调性能

表3 不同码率的编码多项式

图7 不同卷积编码码率下差分BPSK调制解调的性能

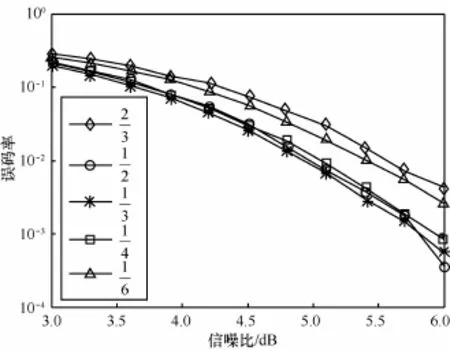
图8 不同卷积编码码率下差分QPSK调制解调的性能

4.2 不同码率Turbo编码的差分调制解调性能

图9 不同Turbo编码码率下差分BPSK调制解调的性能

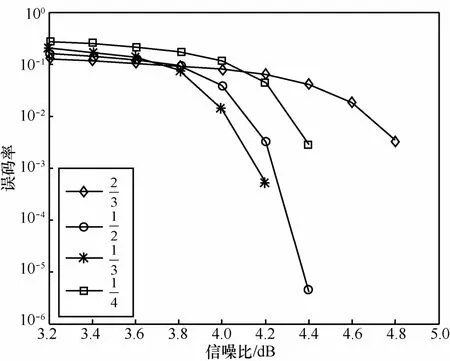
图10 不同Turbo编码码率下差分QPSK调制解调的性能

5 结束语

差分调制解调是无线通信中可靠性和有效性传输的一种折衷的方法。面向差分调制解调的编码码率既不宜过高，也不宜过低。本文从信息论的角度，求出各种码率下的香农限，得出编码码率在时，差分BPSK和差分QPSK调制解调的性能最优，并采用不同码率下的卷积编码和Turbo编码，仿真验证了这一结论。

本文的工作为差分调制解调时编码码率的选取提供了指导。但是，由于实际采用的编码，性能都和香农限有差异，因此针对实际的编码，应在码率附近，仔细仿真后以最终实际编码的性能为准，选取最优的码率。从这个意义上说，本文的工作为编码码率的选取提供了一个启发指导。

［1］ 陈文龙. 高动态多进制扩频系统的关键技术研究［D］. 西安： 西安电子科技大学，2009. CHEN W L. Study of key technology of high dynamic multi-band spread spectrum system［D］. Xi'an： Xidian University， 2009.

［2］ 胡东伟， 陈杰， 石寅， 等. BPSK调制高动态遥测接收机的设计［J］. 电子科技大学学报， 2011， 40（5）： 691-696. HU D W， CHEN J， SHI Y， et al. Design of BPSK modulate high dynamic telemetry receiver［J］. Journal of University of Electronic Science and Technology， 2011，40（50）： 691-696.

［3］ 胡东伟， 王力男， 王永超. 一种基于并行导频的短突发传输方法［J］. 无线电通信技术， 2015， 41（6）： 50-53. HU D W，WANG L N，WANG Y C. A transmitting method based on parallel pilot short burst［J］.Wireless Communication Technology，2015， 41（6）： 50-53.

［4］ 沈连丰， 叶芝慧. 信息论与编码［M］. 北京： 科学出版社， 2004：146-148.SHEN L F， YE Z H. Information theory and coding［M］. Beijing：Science Press， 2004： 146-148.

［5］ 杨志敏. 逼近香农限的检测解码算法与差错控制技术研究［D］.杭州： 浙江大学， 2009. YANG Z M. Research approaching shannon limit of detection code algorithm and error control technology［D］. Hangzhou： Zhejiang University， 2009.

［6］ LIANG C L， MA X， ZHUANG Q T， et al. Spatial coupling of generator matrices： a general approach to design good codes at a target BER［J］. IEEE Transmition On Communication， 2014， 62（12）：4211-4219.

［7］ MARVIN K. Probability distributions involving gaussian random variables： a handbook for engineers and scientists［M］. Berlin：Springer， 2006：49.

［8］ 李博纳， 赵新泉. 概率论与数理统计［M］. 北京： 高等教育出版社， 2006：81. LI B N， ZHAO X Q. Probability and mathematical statistics［M］. Beijing： Higher Education Press，2006：81.

［9］ 王新梅， 肖国镇. 纠错码——原理与方法［M］. 西安： 西安电子科技大学出版社， 2001：413. WANG X M， XIAO G Z. Error correcting code， principles and methods［M］. Xi'an： Xidian University Press， 2001：413.

［10］ TOMLINSON M， RG'H'EFF M. A quasi coherent spread spectrum decoder for satellite communications using a low rate convolutional code ［J］. IEEE the 4th International Symposium on Spread Spectrum Techniques and Applications， 1996（2）： 570-574.

［11］ 王晓涛， 刘振华. 基于可信位置排序的咬尾卷积码译码算法［J］.电子与信息学报， 2015， 37（7）： 1575-1579. WANG X T， LIU Z H. Biting tail convolution code decoding algorithm based on trusted position sort［J］.Journal of Electronics & Information Technology， 2015， 37（7）： 1575-1579.

［12］ WANG X T， QIAN H， XIANG W D， et al. An efficient ML decoder for tail-biting codes based on circular trap detection［J］. IEEE Transmition On Communication， 2013， 61（4）： 1212-1221.

［13］ 3GPP TS 25.212. Multiplexing and channel coding（FDD）［S］. 1999.

［14］ 胡东伟. 极低码率Turbo及其应用［J］. 无线电工程， 2014， 44（12）：1-3. HU D W. Very low bit rate Turbo and its application［J］.Radio Engineering of China，2014，44（12）：1-3.

徐亚冲（1984-），男，山东肥城人，硕士，中国电子科技集团公司第五十四研究所工程师，主要研究方向为无线通信、卫星通信。

胡东伟（1980-），男，湖北麻城人，博士，中国电子科技集团公司第五十四研究所高级工程师，主要研究方向为无线通信理论、集成电路设计。

On the coding rate for differential modulation and detections

XU Ya-chong， HU Dong-wei
（The 54th Research Institute of CETC， Shijiazhuang 050081， China）

Differential demodulation is an important method of solving the information transmission which is used in the high dynamic condition of the wireless communication. The coding rate for differential modulation and detections neither be too high， nor be too low. To find the optimal coding rate， the Shannon limit of error free transmissions with different rates for differential BPSK and differential QPSK were derived. Thereafter， the optimal coding rate was obtained from the view point of information theory. Convolutional codes and Turbo codes with different rates were employed， and simulations were conducted for the verification of the result.

differential demodulation， coding rate， convolutional code， Turbo code

TP393

A

10.11959/j.issn.2096-109x.2016.00072

2016-05-07；

2016-07-02。通信作者：徐亚冲，chongge006@163.com