Eshelby夹杂理论在岩石损伤本构研究中的应用★

柏　准

(解放军理工大学国防工程学院爆炸冲击防灾减灾国家重点实验室，江苏 南京　210007)



Eshelby夹杂理论在岩石损伤本构研究中的应用★

柏准

(解放军理工大学国防工程学院爆炸冲击防灾减灾国家重点实验室，江苏 南京210007)

结合岩石本构的研究历程，论述了Eshelby夹杂理论在岩石损伤力学应用研究中的最新进展，分析了不同平均场方法的优缺点，探讨了夹杂理论在岩石损伤本构研究中的应用前景，指出Mori-Tanaka法进行岩石细观损伤研究的优越性。

夹杂理论，岩石损伤力学，等效弹性模量

岩体本构是外界荷载引起岩体变形的数学描述，是解决工程实践中岩石力学问题的基础。在研究初期，岩石被看作均匀完整的连续介质，一般采用经典的弹塑性力学来描述其应力应变的关系，用强度准则来表征岩体破坏的应力应变状态。随着认识水平的发展，岩石内部微观缺陷对其力学行为的影响越来越受到研究者的重视，损伤力学随即被引入岩石力学。

岩石损伤力学主要用于描述岩体的非线性和非连续性，因其立足点和研究尺度不同可分为宏观损伤力学(CDM)和细观损伤力学(MDM)，两者的不同主要体现在损伤变量的定义上。宏观损伤力学唯象地将岩石缺陷演化与力学行为联系起来，定义宏观损伤变量，由K.yoya[1]于1985年首次引入岩体力学，将损伤变量定义为岩石不连续面面积的减少；在国内，周维垣等[2]首次将损伤力学用于构建岩石本构，基于裂隙统计定义损伤张量；李新平[3]将断裂力学引入岩石损伤研究，较好地解决了岩体内部裂隙的损伤效应。20世纪90年代以来，因细观损伤力学能解释岩石细观结构的变化而逐渐获得重视，其中王金龙等[4]将损伤变量定义为裂纹引起的体积应变和基体体积应变之比，分析岩石裂纹的扩展作用；冯夏庭等[5]以孔隙率为微损伤变量，建立化学腐蚀下的岩石细观损伤本构关系；谢和平[6]首次运用分形几何定量损伤，用于研究岩石微观断裂机理与宏观变形的关系。Eshelby夹杂理论作为研究非均质材料的重要细观理论模型，也引起了岩石力学研究者的注意，本文将对Eshelby夹杂理论及其衍生的Mori-Tanaka平均场方法在岩石损伤力学中的应用现状及前景进行综述与展望。

1　Eshelby夹杂理论的基本概念

Eshelby夹杂理论对于非均质材料(如复合材料)的研究有着非常重要的意义。由于缺乏对于材料微观结构的全面描述，细观力学及其复合材料力学只能根据材料有限的微结构信息建立局部化关系，利用平均化思想，选取代表性体积单元RVE，将非均质转换为均质，进而对材料的性质进行近似界限分析和近似预测[7]。而大多数平均场方法都是将多个夹杂问题转换为代表性体积单元中的单夹杂问题，则关于单夹杂问题的Eshelby解成为许多细观模型，如Mori-Tanaka模型[8]，Taylor模型[9]，自洽模型[10]的重要基础。1957年英国科学家Eshelby首次给出椭球夹杂问题的显示解，提出本征应变概念，指出夹杂物应变场与基体应变场之差ε差与本征应变ε*之间存在以下关系[11]：

ε差=S∶ε*

(1)

其中，S为Eshelby张量，与夹杂物的形状和基体性质有关，其长径比α不同可表示针状(α→∞)、球状(α=1)或者裂纹(α=0)等。而细观力学平均场方法是基于多尺度的，将夹杂应变ε和宏观应变E通过局部化张量A联系起来：

ε(x)=A(x)∶E

(2)

其中，A取决于不同的平均场方法，其中Taylor法计算方便，但无法考虑夹杂相互作用，只适合稀疏夹杂的情况；自洽法形式简单，但过高估计夹杂相互作用对材料刚度的影响；IDD和PCW可考虑夹杂间空间分布，但计算较为复杂。而Mori-Tanaka法采用背应力概念考虑夹杂相互作用，该方法物理概念清晰，逐次迭代可提高精度，针对非圆形夹杂，利用正交化可考虑夹杂各向异性等多方面优越性，受到广泛关注。Mori-Tanaka平均场方法还被进一步拓展，用于研究复合材料的细观损伤机理，例如赵颖华[12]以Eshelby夹杂理论和Mori-Tanaka法为基础，针对不同的细观损伤模式，建立了复合材料损伤弹性和弹塑性力学理论。复合材料损伤理论的不断发展，为其他非均质材料的研究提供了有益的借鉴与启示。

2　Eshelby夹杂理论在岩石损伤本构研究中的应用现状

岩石内部存在着孔隙、裂隙和节理等细微观缺陷，作为非均质材料的力学行为越来越受到学者的重视。随着CT等技术用于岩石内部探测，人们对岩石细观结构有了更加直观的认识。细观损伤力学作为研究岩石细观结构变化的主要理论不断获得发展，采用Eshelby夹杂理论分析岩石的损伤力学特性也正处于积极探索阶段。比如针对脆性岩石内部已有裂纹的扩展与新裂纹的萌生是非线性力学行为产生的主要原因，ZHU[13]运用Eshelby夹杂问题解，将微裂纹近似为币形夹杂(α=0)，构建了细观力学损伤模型的热动力学框架，考虑基体的弹性应变εm和裂纹产生的非弹性应变εc，得到代表性体积单元自由能的一般形式：

(3)

其中，Cm为基体模量；Cb为四阶有效弹性张量。

该细观损伤模型能够很好的解释岩石材料损伤的各项异性、裂纹的闭合和张开等现象，但无法考虑裂纹的空间分布效应和不同族裂纹间相互影响。陈益峰等[14]将上述模型拓展到非等温条件，引入微裂纹的法向闭合条件和滑动剪涨条件，分别运用M-T法和Taylor法推导出有效热传导张量，建立了热—力耦合条件下岩石的细观损伤力学模型。而针对节理岩体内部结构面广泛分布、数量多而规模小的特点，朱福巍[15]将结构面简化为圆盘夹杂，利用本构积分算法，得到节理岩体的增量型本构关系：

(4)

(5)

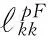
该损伤本构关系虽然考虑了破坏岩体的承载力，但是由于Eshelby理论解不适用夹杂比例较大的情况，造成模型模拟结果与试验结果在后期有较大出入。

3　Eshelby夹杂理论在岩石损伤本构研究中的前景分析

(6)

L等=L0{I-φ[(L1-L0)(φ+(1-φ)S+L0)]-1(L1-L0)-1}

(7)

其中，I为四阶单位张量；S为Eshelby张量。将式(7)代入式(6)可知孔隙岩石的损伤变量是孔隙度的函数，只要选取合适的孔隙动态演化模型就可探究孔隙岩石细观损伤规律。此外，Eshelby夹杂理论还可用于岩石动态特性及其本构特性的研究，从细观损伤角度分析岩石内部缺陷在动态荷载作用下的力学响应。从细观损伤角度出发，主要是指不考虑岩石的粘性，基于夹杂理论和动态断裂理论，根据裂纹扩展速率公式和平均场方法建立模型。同样为准脆性材料的混凝土已有此方面的研究，比如刘海峰等[17]将混凝土看成实体和裂纹组成的复合材料，基于Eshelby夹杂理论和M-T法建立了冲击荷载作用下混凝土材料的动态本构模型，并进行了应变率相关性研究，该本构模型具有物理概念清晰、参数便于试验确定的特点，对宏—细观结合的岩石动态损伤研究具有重要参考意义。

4　结语

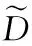
[1]K.yoya,T.An alication of damage tensor for estimating mechanical properties of rock mass(in Japanese),civil conference,1985,10(6)：358-363.

[2]周维垣,杨若琼,周力田.节理岩体和拱坝坝肩稳定的断裂力学分析[J].岩石力学与工程学报,1986(4):377-388.

[3]李新平.多裂隙岩体的等效连续弹性损伤断裂模型强度特性及有限元分析[D].武汉：中科院武汉岩土所博士论文,1990.

[4]王金龙,林卓英,吴玉山,等.脆性岩石的损伤与裂隙扩展[J].岩土力学,1990(3):1-8.

[5]冯夏庭,丁梧秀.灰岩细观结构的化学损伤效应及化学损伤定量化研究方法探讨[J].岩石力学与工程学报,2005(8):1283-1288.

[6]谢和平.分形—岩石力学导论[M].北京:科学出版社,1997.

[7]胥柏香.Eshelby夹杂问题特殊性质的研究[D].北京：北京大学,2008.

[8]Mori T,Tanaka K.Average stress in matrix and average elastic energy of materials with misfitting inclusion[J].Acta Metall,1973(21):571-574.

[9]Hill R.Continuum micro-mechanics of elastoplastic polycrystals[J].Mech.phys.Solids,1965(13):89-101.

[10]Christensen R.M.Lo K.H.Solutions for effective shear properties in three phase sphere and cylinder models[J].Mech.Phy.Solids,1979,27(3)：15-330.

[11]Eshelby J D.The determination of the elastic field of an ellipsoidal inclusion,and related problem[J].Proc Royal SocLond A,1957(421):376-396.

[12]赵颖华.复合材料损伤细观力学分析[D].北京：清华大学,1996.

[13]ZHU Q Z.Applications of homogenization approaches to 3D damage modelling of quasi-brittle materials：formulation，validations and numerical implantations[Ph.D.Thesis][D].Lille：Université des Sciences et Technologies de Lille，2006.

[14]陈益峰,李典庆,荣冠,等.脆性岩石损伤与热传导特性的细观力学模型[J].岩石力学与工程学报,2011(10):1959-1969.

[15]朱福巍.节理岩体细观损伤模型的理论研究与数值方法[D].北京：北京交通大学,2011.

[16]赖勇.岩石(体)宏细观复合损伤理论与应用研究[D].重庆：重庆大学,2008.

[17]刘海峰,宁建国.冲击载荷作用下混凝土本构模型(英文)[J].Journal of Southeast University(English Edition),2012(1):79-84.

On application of Eshelby hybrid theory in constitutive research on rock damages★

Bai Zhun

(KeyLabforExplosionShockDisasterPreventionandMitigation,DefenseEngineeringCollege,PLAUniversityofScienceandTechnology,Nanjing210007,China)

Combining with the research on the rock constitutive structure, the paper indicates the latest progress of Eshelby hybrid theory in rock damage dynamics, analyzes the advantages and disadvantages of various mean fields, explores the application prospect for the theory in the constitutive research of rocks, and points out the priority of adopting Mori-Tanaka method in the microscopic damage of rocks.

hybrid theory, rock damage dynamics, effective elastic property

1009-6825(2016)08-0081-03

2016-01-07★：江苏省自然科学基金(项目编号：BK20141067)

柏准(1991- )，男，在读硕士

P584

A