基于有限元法对边坡稳定敏感性参数的分析★
范福广 张新春
(1.中建三局安装工程有限公司,湖北 武汉 430000; 2.华北电力大学,河北 保定 071003)
基于有限元法对边坡稳定敏感性参数的分析★
范福广1张新春2
(1.中建三局安装工程有限公司,湖北 武汉430000;2.华北电力大学,河北 保定071003)
采用有限元强度折减法,从计算范围、内摩擦角、粘聚力、土体重度、坡高与坡度等方面,研究了计算敏感性参数对山区边坡稳定性安全系数的影响,结果表明,土体的粘聚力、内摩擦角和重度对边坡稳定性的影响最为敏感,坡角与坡高的影响次之,计算范围的影响最小。
边坡稳定性,安全系数,强度折减法,敏感性参数
为了解决能源分布不均匀和经济发展不平衡的现状,我国提出了“西电东送”这一伟大工程。“西电东送”不仅可以满足东部地区发展的电力需求,而且还有利于东部地区电力结构的战略性调整,从而实现电力的可持续发展。但由于西部地区地形复杂多变,在输电过程中,杆塔基础不可避免的要建在山顶或半山坡等地形上,这样就会面临着塔位边坡稳定性问题。因此,对山区边坡的稳定性进行分析,并评估其敏感性参数的影响程度,对于边坡稳定性治理方法及其技术经济特性,有着重要的工程意义和实践价值。
随着计算机技术的发展,有限元强度折减法已成为研究山区边坡稳定性的一种有效的数值分析方法,并被广泛的推广和应用。基于这一方法,许多学者在边坡稳定性方面做了大量的工作,并得到了一些最新的成果[1-8]。例如,郑颖人等[1]首先利用有限元强度折减法对边坡稳定性的安全系数进行了研究,并将该方法应用于岩质边坡的稳定性分析[2];侯连成等[3]对某变电所的边坡稳定性进行了分析;董璞等[4]对有限元强度折减法的边坡稳定性分析精度进行了探讨;杨铭键等[5]基于两种有限元软件对边坡的稳定性进行了对比分析。针对目前山区输电线路铁塔塔位边坡的实际特点,曾二贤等[6]采用FLAC/Slope软件数值模拟了塔位边坡分步开挖的施工过程,并对塔位边坡处理方法及技术进行了分析[7]。然而如何通过对山区输电线路的边坡稳定性的分析,得出其影响参数的敏感性,对于山区边坡失稳的预防和治理都是非常重要的。基于以上分析,本文以均匀土体介质为例,采用强度有限元折减法对边坡稳定性进行了分析。通过对山区边坡达到极限破坏状态的判定,求得边坡稳定安全性系数,从而分析出计算参数对山区边坡稳定的敏感性。
1 有限元强度折减法
1.1有限元强度折减法的基本原理
强度折减法是由Duncan于1996年提出的,他指出边坡的安全系数Fs可定义为使边坡刚好达到临界破坏状态时,对土体材料抗剪强度进行折减的程度。基本原理就是逐渐减小土体的剪切强度参数(也就是逐渐增大折减系数)直至土坡发生破坏,换一种说法就是当边坡的塑性变形贯穿于边坡上的某一个平面时,其减少的倍数(即临界折减系数)就被定义为安全系数。对于土体强度折减的基本公式主要有以下两个,分别为:
(1)
(2)
其中,C为粘聚力;φ为内摩擦角;C′为折减后的粘聚力;φ′为折减后的内摩擦角;F为强度折减系数。强度折减技术的要点[8]就是假定外载不变,利用式(1)和式(2)来折减土体的强度指标C和φ,然后对边坡进行数值分析,通过不断地增加折减系数F,反复进行应力应变分析,直到边坡破坏,此时的折减系数为安全系数Fs。
1.2有限元中边坡破坏的判据
目前,有限元强度折减法已经成为边坡稳定性分析的一种有效数值分析方法。在有限元计算结果的基础上,如何判定边坡达到极限破坏状态已经成为边坡稳定性分析的关键问题。目前主要有三种判断方法[8]:1)采用有限元计算力和位移迭代不收敛作为失稳依据;2)以塑性应变从坡脚至坡顶塑性区是否贯通作为判据;3)以某一特征部位的最大位移或最大塑性应变随着折减系数的增加发生了突变作为边坡失稳的破坏标志。以上三种判据得到的安全系数相差不大。有限元强度折减法就是通过不断对岩土强度指标进行折减得到新的强度指标,然后将折减后的指标代入有限元模型中,若程序收敛,则岩土处于稳定状态;继续增大折减系数,得到新的强度指标,代入有限元模型中计算,如此反复,直到程序不收敛。该边坡的稳定性安全系数即为程序恰好在收敛与不收敛的临界点时的折减系数。然而,塑性区贯穿并不一定意味着破坏,塑性区贯穿是破坏的必要而非充分条件,仍需要看有限元计算的收敛性。第三种判据由于迭代次数,容许限值等影响也存在很大的偏差。可见,虽然第一种判据因为收敛准则的不同会引起安全系数的差异,但可把有限元计算是否收敛作为边坡破坏的依据。本文拟通过一些工程算例来分析边坡稳定性敏感参数的影响。
2 山区边坡稳定敏感性参数分析
2.1有限元模型
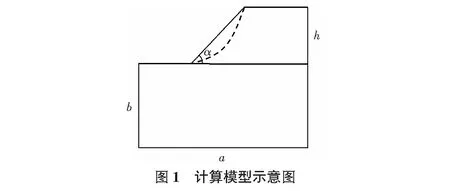
某工程山区边坡如图1所示,坡高为h,坡角为α,该边坡沿竖直方向的计算深度为b,水平方向的计算宽度为a。该边坡考虑为一均匀土体介质,其材料参数如表1所示。

表1 土体物理力学参数
该计算模型为二维均质边坡,利用商业有限元软件ANSYS对山区边坡稳定中的参数敏感性进行了分析。计算过程中,左右两侧边界为水平约束,下部边界为X和Y方向位移约束,上部为自由边界。按平面应变问题进行数值模拟分析,求解器选用稀疏矩阵求解器(Sparse Matrix Direct Solver),并选用全牛顿—拉普森迭代方法。同时采用非关联流动法则,力和位移同时收敛的收敛准则进行计算,力和位移的收敛容许限值均取为0.001。具体研究了计算敏感性参数(包括强度参数和几何参数)对山区边坡稳定性的影响。需要指出的是,当研究某一敏感参数的影响时,人为改变这一参数,其余敏感参数指标不变。
2.2边坡失稳时判据的判定
为了对边坡失稳时的判据进行判定,文中利用有限元方法对计算尺寸a=120 m,b=80 m和h=20 m时的边坡稳定性进行了分析。表2是对土体进行折减后的结果,其他参数保持不变。

表2 折减以后的土体物理力学参数
当F=1时即为没有折减,要得到边坡的安全系数,就要将折减后的参数代入有限元模型进行分析,由程序的收敛与否判定边坡稳定性。若程序收敛,则边坡稳定,反之则失稳。当稳定性系数F未知而需要试算时,通常采用二分法,这样可以减少试算次数。直到收敛时的折减系数与不收敛时的折减系数之间相差甚小,这时可以认为折减系数较大时的程序为恰好不收敛的边界,则较大的折减系数就是该边坡的安全系数。

图2是折减系数分别为3.5和3.53时的收敛过程图。图2中显见,当F=3.5时,程序是收敛的;当F=3.53时,程序已不收敛。
边坡的稳定性系数还可以通过塑性应变区的发展情况来进行校核,一般情况下,当边坡的塑性应变发展为一个贯通的曲面时,边坡就已经失稳,此时将会沿着塑性应变区破坏。在图3中,当F=3.5时,其边坡塑性应变云图没有贯穿;当F=3.53时,边坡塑性应变云图已经贯穿,说明此时边坡已经不稳定。
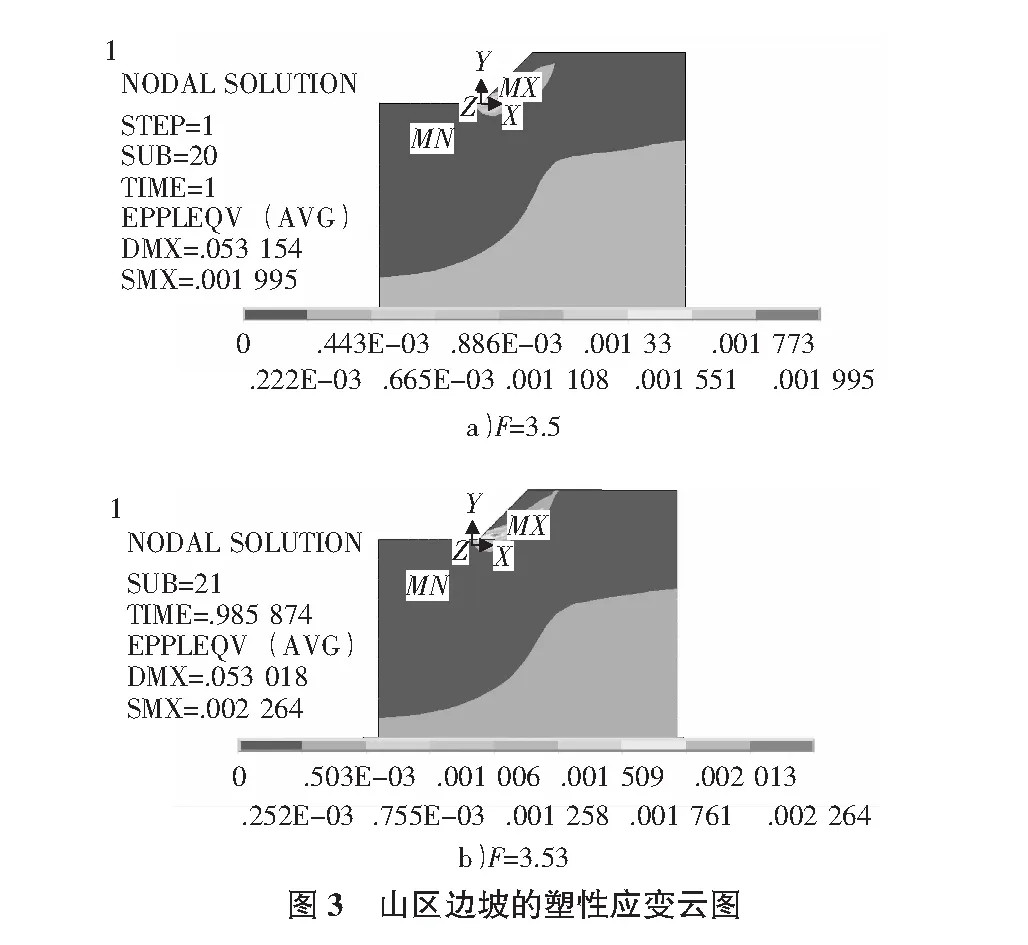
综合图2和图3可知,当a=120 m,b=80 m和h=20 m时,该边坡的稳定安全系数为Fs=3.53。基于以上分析,本文具体讨论了不同敏感性参数对山区边坡稳定性的影响。
2.3不同敏感性参数对山区边坡稳定性的影响
2.3.1内摩擦角的影响
内摩擦角是土体抗剪强度一个非常重要的参数指标。内摩擦角可定义为岩体在重力作用下发生剪切破坏时错动面的倾角,反映的是土体中颗粒间相互移动和胶合作用形成的摩擦特性,其值为强度包线与水平线的夹角。为了反映土体内摩擦角对安全系数的影响,文中取了7组不同内摩擦角数值,其他参数不变,利用强度折减有限元法对其对应的安全系数进行了分析。图4给出了土体内摩擦角和内摩擦角的正切值与山区边坡安全系数的影响关系曲线。图4中显见,安全系数Fs与土体内摩擦角φ(或tanφ)几乎呈直线关系,随着土体内摩擦角的增大而增大。可见,土体的内摩擦角对于山区边坡稳定性较敏感。
2.3.2土体粘聚力的影响
粘聚力C一般由土粒之间的胶结作用或电分子引力等因素形成,通常与土体中的粘粒含量、矿物成分、含水量和土的结构等因素密切相关。粘聚力亦是影响边坡稳定性的一个重要参数指标。为了研究粘聚力的影响,文中取了5组不同数值,其他参数保持不变。图5给出了粘聚力与安全系数间的关系。图5中显见,安全系数近乎直线地依赖于粘聚力,安全系数随着粘聚力的增加而线性增加。研究表明,无论粘聚力的大小如何,由粘聚力和安全系数所决定的点都较为完好地符合这条直线。

2.3.3土体重度的影响
图6给出了土体的重度对山区边坡安全系数的影响。当土体重度增加时,边坡土体的安全系数将随之减小,也就是降低了边坡的稳定性。由图6可知,安全系数与土体的重度构成一条上凹的曲线。实际上,边坡安全系数关于重度的曲线应该是坐标系中的一段孤立的曲线段,不能向两端无限延伸。当土体重度逐渐增大时,安全系数的变化趋于平缓,也就是说,边坡安全系数对土体重度的敏感性将逐渐降低。
2.3.4坡高与坡度的影响
坡高为边坡坡顶到坡脚的垂直距离,一般用h来表示,如图1所示。图7给出了坡高h对山区边坡稳定性的影响。由图7可知,坡高h与安全系数Fs的关系曲线与反函数(或双曲线关系)相似,安全系数Fs随着坡高h的增大而减小。并且,随着坡高的增大,安全系数曲线逐渐变得平缓,即安全系数对坡高的敏感性逐渐降低。

坡度就是边坡坡面的倾斜程度,是地表单元陡缓的程度。文中用坡角的度数来表示坡度。研究表明,当坡角很小时,边坡的稳定性较好,即安全系数较大,这对研究边坡的稳定性意义不大;当坡角很大时,此时的边坡极不稳定,极容易发生失稳破坏,这对研究边坡的稳定性也意义不大。本文中具体研究了坡角在30°~70°范围内,坡角对安全系数的影响。图8中显见,坡角α和安全系数Fs之间的关系亦与反函数(或双曲线)关系相似,安全系数Fs随着坡角α的增大而减小。由于该曲线不可能向两端无限延伸,随着坡角的增大,安全系数也逐渐趋于平缓,即安全系数对坡角的敏感性逐渐降低,但影响程度要大于边坡的高度。

2.3.5计算范围的影响
所谓的计算范围就是指图1中a和b的值。改变a和b的值将会对边坡的稳定性产生一定的影响。文中取了5组不同的a值和b值。利用强度折减有限元法对安全系数进行了讨论,图9给出了计算范围对边坡安全系数的影响曲线。当计算范围不大时,无论增加X或Y方向的尺寸,其安全系数都相应的增大。但当尺寸增加到一定程度时,对安全系数的影响不敏感。
从图4~图9可知,内摩擦角φ及粘聚力C与安全系数Fs的关系都接近于线性关系,对安全系数最为敏感;当土体重度γ较大时,对安全系数也较敏感;坡高及坡角与安全系数的关系和双曲
线近似,随着坡高与坡角的增加,曲线逐渐平缓。当坡高与坡角较小时,由于边坡的破坏形式可能不是失稳滑坡,所以其安全系数较大,但随着坡高与坡角的增大,安全系数对其敏感性逐渐降低,因此安全系数对坡高与坡角的敏感性仅次于土体的内部物理参数(即土体内摩擦角、粘聚力和土体重度);计算范围与安全系数的关系近乎是水平直线关系,对安全系数的影响最小。

3 结语
本文利用强度折减有限元法对影响边坡稳定性的敏感性参数进行了分析。研究结果表明,与几何因素相比,土体物理力学参数(例如土体、粘结力和土体重度)对山区边坡稳定性安全系数的影响较为敏感。在几何参数中,边坡角α的敏感度要大于坡高h和计算尺寸;在土体物理力学参数中,土体的内摩擦角φ的敏感度最大,土体的重度γ和粘聚力C次之。本文结论将为山区输电铁塔基础的合理设计以及边坡治理提供重要的理论依据。
[1]赵尚毅,郑颖人,时卫民,等.用有限元强度折减法求边坡稳定安全系数[J].岩土工程学报,2002,24(3):343-346.
[2]郑颖人,赵尚毅.有限元强度折减法在土坡与岩坡中的应用[J].岩石力学与工程学报,2004,3(19):3381-3388.
[3]侯连成,王笑二,王家伟,等.基于强度折减法的某变电所边坡稳定性分析[J].水文地质工程地质,2012,9(1):72-74.
[4]董璞,刘金龙,李亮辉.强度折减有限元法分析边坡稳定性的精度探讨[J].四川建筑科学研究,2009,35(2):146-150.
[5]杨铭键,余贤斌,黎剑华.基于ANSYS与FLAC的边坡稳定性对比分析[J].科学技术与工程,2012,12(24):1671-1815.
[6]曾二贤,舒爱强,廖文炜.基于FLAC/Slope模拟分析输电线路塔位边坡的开挖稳定性[J].电网与清洁能源,2011,27(4):14-18.
[7]曾二贤,陈治,胡星,等.山区输电线路塔位边坡治理方法及技术经济分析[J].能源技术经济,2010,22(10):20-25.
[8]聂守智,袁继国,要创,等.基于有限元强度折减法边坡失稳的数值试验研究[J].电网与清洁能源,2009,25(12):91-94.
Analysis of slope stability sensitivity parameters based on the Finite Element Method(FEM)★
Fan Fuguang1Zhang Xinchun2
(1.InstallationEngineeringCompany,ChinaStateConstructionEngineeringCop.theThirdBureau,Wuhan430000,China; 2.NorthChinaElectricPowerUniversity,Baoding071003,China)
Using the finite element strength subtraction method, from the calculation scope, internal friction angle, cohesive force, soil weight, slopeheight andgradient and other aspect, researched the influence of calculation of sensitivity parameters to mountain slope stability safety coefficient, the results showed that the influence of soil cohesive force, internal friction angle and weight was the most sensitive to slope stability, the influence of slope angle andgradient took second place, the influence of calculation was smaller.
slope stability, safety factor, strength reduction, sensibility parameters
1009-6825(2016)08-0078-03
2016-01-07★:中央高校基本科研业务费专项资金资助项目(项目编号:2014MS117)
范福广(1984- ),男,工程师;张新春(1980- ),男,副教授
TU432
A

