具有均匀Dzyaloshinskii-Moriya相互作用的一维反铁磁链的孤子激发
汪 森, 陈 浩, 王瑞强
(华南师范大学物理与电信工程学院,广州 510006)
具有均匀Dzyaloshinskii-Moriya相互作用的一维反铁磁链的孤子激发
汪森, 陈浩*, 王瑞强
(华南师范大学物理与电信工程学院,广州 510006)

孤子; 反铁磁链; 多重尺度法
准一维磁体的孤子激发在理论研究上取得了重大成果,体现在2个方向:(1)一维海森伯铁磁链中的孤子解[1-5];(2)一维海森伯反铁磁链中的孤子解[6-8].其基本思想均考虑一维海森伯磁性链,在存在非线性作用(交换作用各向异性、Aharonov-Bohm效应等)时,再考虑外磁场的影响,求出此时磁性链所具有的孤子解.
对于一维反铁磁物质来说,超交换作用非常重要.克拉默斯[9]认为:反铁磁性物体内部磁性离子之间的交换作用是以隔在中间的非磁性离子为媒介来实现的,并命名为超交换作用,同时提出超交换作用模型,用于解释反铁磁自发磁化的起因.Dzyaloshinskii-Moriya(DM)相互作用是一种各向异性超交换相互作用[10-11],存在于许多反铁磁体与弱铁磁体中,如CuGeO3、La2CuO4、Cs2CuCl4、BaCu2Si2O7等,根源于粒子自旋和轨道耦合的反对称性, MORIYA[11]5在1960年提出了DM相互作用的表达式:

(1)其中,Di,j为DM相互作用矢量,反对称,即Di,j=-Dj,i,Si和Sj分别为格点i和格点j上的自旋矢量.
氧化铜超导体中低温相的弱磁性、相变问题与DM相互作用有关,而且它在量子点量子计算中也起着重要的作用.在反铁磁链模型[9-11]中,DM相互作用都是交错的,对应哈密顿量为:
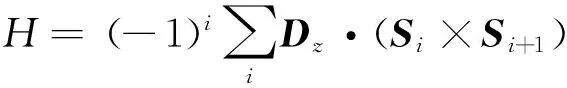
(2)
其中,取DM相互作用的方向为Z方向,即Dz=(0,0,D).然而近年随着对磁性材料探讨的深入,人们发现,部分反铁磁体(TiOCl等)在垂直于DM相互作用矢量方向的外磁场作用下,也有可能存在均匀DM相互作用[12-13]. 此后,对该情况下的反铁磁体的零温相图,所用的反铁磁体的哈密顿量[14]2为:

(3)
由于式(3)描述了反铁磁体一种不同以往的新现象,求式(3)的孤子解很有必要,但其求解极其困难,如果磁场是弱磁场,对应的Zeeman能小于DM相互作用能,粗略计算时忽略Zeeman能,式(3)就变成了具有均匀DM相互作用的一维反铁磁链,此时可求出其孤子解.
本文求出了具有均匀DM相互作用的一维反铁磁链的椭圆函数波解和对应孤子解,并且讨论了DM相互作用对一维反铁磁链孤子解的影响.为求解计算过程中出现的非线性方程组,利用了多重尺度方法[15].已知利用多重尺度方法可求出非线性薛定谔方程的包络孤子解[16]以及Aharonov-Bohm磁通对反铁磁链中的孤立子的影响[17].
1 模型的哈密顿量和运动方程


(4)


(5)
假设a、b子格中自旋分别沿+Z、-Z方向,利用Holstain-Primakoff变换[20]

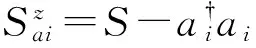
(6)


(7)

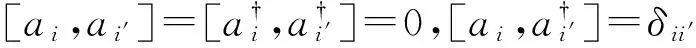


(8)


(9)
利用海森伯运动方程[21],得到算符al、bl的运动方程为

(10)

(11)
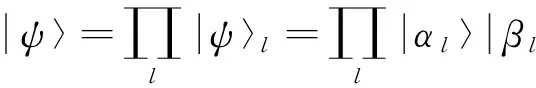
(12)
算符al、bl的本征方程为

(13)
利用式(13),可将式(10)、(11)化为
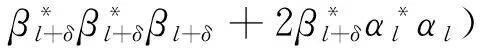
(14)

(15)
2 多重尺度方法求解
利用准分立近似和多重尺度相结合的方法[16]83,将αl(t)和βl(t)按以下方式展开:
yl(t)=εy(1)(t,ξl,θl)+ε2y(2)(λ,ξl,θl)+…=
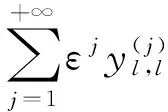
(16)

(17)

把式(16)、(17)代入式(14)、(15),并比较ε的不同幂次项.
(1)比较ε的一次项,得到

(18)

(19)
由式(18)、(19)可假设

(20)

(21)
式中

(22)

(23)
(2)比较ε的二次项,并结合式(20)、(21)得到



(24)


(25)
由式(24)、(25)可得
-i[2ωvg+2A1(4DSdcoskd-4JSdsinkd)×

(26)
其中,等号右端含有诱发久期项的exp(iθl),为了消除久期项,要求右端方括号内的值为0,得到
vg=

(27)
式(27)满足vg=dω/dk. 由式(24)、(25),可假定

(28)

(29)
(3)比较ε的三次项,并结合式(20)、(21)、(24)、(25)、(28)、(29)得到
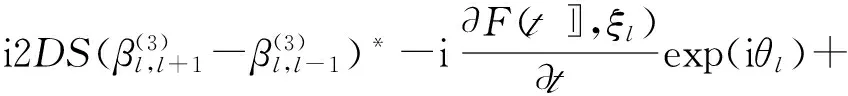

(30)
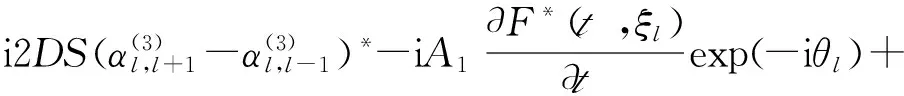
exp(-iθl)-[4A1+3(A1)2coskd+coskd]×

(31)
由式(30)、(31)可得

(32)

(33)

(34)

(35)
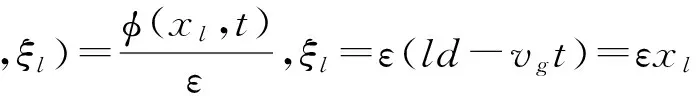
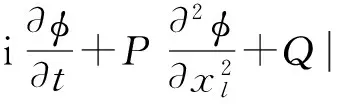
(36)
即标准的非线性薛定谔方程.
3 椭圆函数波解及相应孤子解
当P>0、Q>0时,式(36)具有椭圆函数波解和相应亮孤子解[15]169-173,结合式(16)有

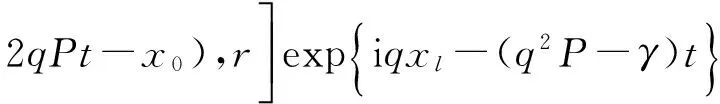
(37)


(38)
其中DN(x,r)被称为第三类Jacobi椭圆函数[23],Ω=qvg+q2P-γ+ω,γ>0,γ,q是待定常数,x0是积分常数.若将所讨论的反铁磁链闭合成1个环,则αl(t)满足周期边界条件:
αl(t)=αl+N(t),
(39)
其中N为元胞个数.将式(39)代入式(38),结合第三类Jacobi椭圆函数的周期性:
DN(μ+2K)=DN(μ),
其中

可得k+q=2nπ/Nd(n=0,±1,±2,…);

当r→1时,即K(r)→∞,Nd→∞,式(37)、(38)化为亮孤子解:



exp{i[(k+q)ld-Ωt]},
(40)

其中Ω=qvg+q2p-γ+ω,γ>0,根据式(12)得
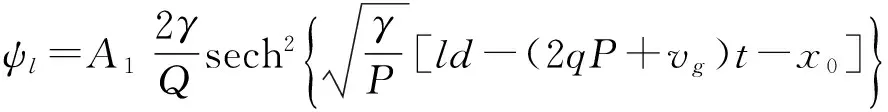
(41)
可将式(41)归一化可得

(42)
由式(40)、(42)可知,对于αl(t)的孤子解,其峰值A、宽度Ls、能量E分别为:

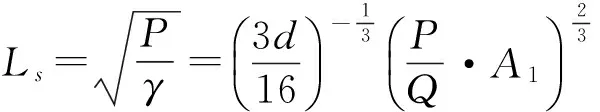

其中ω、A1、vg、P、Q分别由式(22)、(23)、(27)、(34)、(35)表述,解αl(t)代表相速为Ω/(k+q)的振荡波,其包络是1个钟形峰,峰宽由Ls量度,包络中心以速度(2qP+vg)在一维链中传播,传播过程中包络的形状不变,因此φ(xi,t)为包络孤子,Ls代表包络孤子的尺寸.
4 讨论与结论
本文研究了具有DM相互作用的一维反铁磁链,采用反铁磁中常用的双子格模型,在只考虑最近邻作用时,利用Holstain-Primakoff变换、Glauber相干态表示,以及Heisenberg运动方程,得到了1个偏微分方程组,然后应用多重尺度方法,消除久期项时,得到1个非线性薛定谔方程,求出了在一级近似下该模型的椭圆函数波解和孤子解,并求出亮孤子(P>0、Q>0)情况下相应的特征量——孤子宽度、孤子峰值及孤子能量.结果表明,孤子宽度、峰值及能量与DM相互作用的Z分量D的关系非常复杂,与k的取值有关,并不随D的增减而单调增减.
式(22)表明,系统具有2支谱线. 1支为光学支,对应于

另1支为声学支,对应于

明显,-4JS≤ω-≤0≤ω+≤4JS.对于光学支顶部,此时
ω+=4JS,4JS coskd+4DSsinkd=0,
结合式(23)、(35),得到Q=0,代入式(36)知,系统只存在简谐波解,无孤子解;对于声学支底部,此时
ω-=-4JS,4JScoskd+4DSsinkd=0,
同理,得到Q→∞,系统波函数趋于0;对于光学支底部和声学支顶部,有ω+=ω-=0,式(27)中vg→∞,出现奇异性,有待进一步研究.
当D取0时,式(4)表示各项同性的一维反铁磁链,此时式(35)中Q=0,式(36)在一级近似下没有孤子解,这表明:均匀DM相互作用的存在破坏了各项同性.当2qP+vg=0时,式(41)表示的包络振幅不随时间而变化,代表局域模.
[1]PUSHKAROV D I, PUSHKAROV K I. Solitary magnons in one-dimensional ferromagnetic chain[J]. Physics Letters A, 1977, 61(5):339-340.
[2]翁紫梅,陈浩.单离子各向异性影响下的一维铁磁链中的孤子[J].物理学报,2007, 56(4):1911-1918.
WENG Z M, CHEN H. Solitons in a one-dimensional ferromagnetic chain under the influence of single-ion anisotropy[J]. Acta Physica Sinica, 2007, 56(4):1911-1918.
[3]朱善华,黄国翔,徐在新.一维更键Heisenberg铁磁链间隙非线性元激发[J].物理学报,1997,46(10):2036-2046.
ZHU S H, HUANG G X, XU Z X. Nonlinear excitations in one-dimensional Heisenberg ferromagnetic chain with bond alternation[J]. Acta Physica Sinica, 1997, 46(10):2036-2046.
[4]YU X Y,CHEN H. Solitary excitations in one-dimensional ferromagnetic spin chains with biquadratic exchange interaction[J]. Chinese Physics B, 2011, 20(12):Art 120509,7pp.
[5]陈浩, 黄皙恒, 谢元栋. 一维铁磁链的一个改进孤子解[J]. 华南师范大学学报(自然科学版), 2002(2):5-8. CHEN H, HUANG X H, XIE Y D. An improved soliton in one-dimensional ferromagnetic chain[J]. Journal of South China Normal University (Natural Science Edition), 2002(2):5-8.
[6]PANDIT R, TANNOUS C, KRUMHANSL J A. Statistical mechanics of a classical one-dimensional canted antiferromagnet II: Solitons[J]. Physical Review B,1983,28(1):289-299.
[7]LIU W M, ZHOU B L. Solitons in an order-parameter-preserving antiferromagnet[J]. Journal of Physics: Condensed Matter, 1993, 5(12):L149-L156.
[8]LISSOUCK D, NGUENANG J P. Solitary magnon excitations in a one-dimensional antiferromagnet with Dzyaloshinsky-Moriya interactions[J]. Journal of Physics:Condensed Matter,2007, 19(9):357-363.
[9]KRAMERS H A. L’interaction entre les atomes magnétogènes dans un cristal paramagnétique[J]. Physica, 1934, 1(1-6):182-192.[10]DZYALOSHINSKII I. A thermodynamic theory of “weak” ferromagnetism of antiferromagnetics[J]. Journal of Phy-sics and Chemistry of Solids,1958,4(4):241-255.
[11]MORIYA T. Anisotropic super exchange interaction and weak ferromagnetism[J].Physical Review,1960,120(1):91-98.
[12]ZAKHAROV D V, DEISENHOFER J, KRUG VON NIDDA H A, et al. Spin dynamics in the low-dimensional magnet TiOCl[J]. Physical Review B,2006, 73(9): Art 094452,23pp.
[13]GANGADHARAIAH S, SUN J M, STARYKH O A. Spin-orbital effects in magnetized quantum wires and spin chains[J]. Physical Review B,2008, 78(5): Art 054436,23pp.
[14]GARATE I, AFFLECK I. Interplay between symmetric exchange anisotropy, uniform Dzyaloshinskii-Moriya interaction and magnetic fields in the phase diagram of Quantum Magnets and superconductors[J]. Physical Review B,2010, 81(14): Art 144419,20pp.
[15]刘式适,刘式达. 物理学中的非线性方程[M]. 2版. 北京: 北京大学出版社, 2012:127-132.
[16]YOSHIMURA K, WATANABE S. Envelope soliton as an intrinsic localized mode in a one-dimensional nonlinear lattice[J]. Journal of the Physical Society of Japan, 1991, 60(1):82-87.
[17]许长谭. Aharonov-Bohm磁通对反铁磁链中的孤立子的影响[J].数学物理学报,2014, 24(1): 51-57.
XU C T. Effect of the Aharonov-Bohm flux on the solitonin antiferromagnetic chain[J]. Acta Mathematica Scientia,2014, 24(1): 51-57.
[18]JACOBS A E, NIKUNI T.Fluctuation-induced phase in CsCuCl3in a transverse magnetic field:theory[J].Journal of Physics:Condensed Matter,1998,10(28):6393-6404.
[19]AFFLECK I, OSHIKAWA M.On the field-induced gap in Cu benzoate and otherS=1/2 antiferromagnetic chains[J].Physical Review B,1999, 60(2):1038-1056.
[20]HOLSTEIN T, PRIMAKOFF H. Field dependence of the intrinsic domain magnetization of a ferromagnet[J]. Phy-sical Review, 1940, 58(12): 1099.
[21]曾谨言.量子力学[M].4版.北京:科学出版社,2007:162.
[22]GLAUBER R J. Coherent and incoherent states of the radiation field[J]. Physical Review, 1963, 131(6): 2769.
[23]刘式适,刘式达. 特殊函数[M].2版. 北京: 气象出版社, 2003:620-715.
【中文责编:成文英文责编:肖菁】
Soliton Excitation in An One-Dimentional Antiferromagnetic Chain with Uniform Dzyaloshinskii-Moriya Interaction
WANG Sen, CHEN Hao*, WANG Ruiqiang
(School of Physics and Telecommunication Engineering, South China Normal University, Guangzhou 510006, China)

soliton; antiferromagnetic chain; multi-scale method
2015-08-23《华南师范大学学报(自然科学版)》网址:http://journal.scnu.edu.cn/n
国家自然科学基金项目(11174088)
陈浩,教授,Email: chenhao@scnu.edu.cn.
O482.51;O175.29
A
1000-5463(2016)03-0082-06

