Current Reversals of an Underdamped Brownian Particle in an Asymmetric Deformable Potential∗

Chun-Chun Cai(蔡纯纯),Jian-Li Liu(刘建立),Hao Chen(陈浩),and Feng-Guo Li(李丰果)

Guangdong Provincial Key Laboratory of Quantum Engineering and Quantum Materials,School of Physics and Telecommunication Engineering,South China Normal University,Guangzhou 510006,China

1 Introduction

When a system at rest is perturbed by an external force,it usually responds by moving in the direction of that force.However,in many situations,the quite surprising contrary behavior in the form of a permanent motion against a(not too large)static force of whatever direction is known as absolute negative mobility.The absolute negative mobility is impossible in a heat-balanced system because it violates the second law of the thermodynamics.Therefore,the study of the absolute negative mobility in the ratchet has aroused much attention in theoretical and experimental physics.[1−7]

The phenomena of the absolute negative mobility are showed in many different cases.In a spatially symmetric and periodic system,which is far from thermal equilibrium,it is discovered that the average particle velocity of the single Brownian particle is positive for negative force and negative for positive force.[1]When several inertial Brownian particles move in a symmetric periodic potential under the in fl uence of a time periodic and a constant,biasing driving force,thermal equilibrium fl uctuations can cause the absolute negative mobility.[2]The overdamped motion of Brownian particles is analysed in the one-dimensional system with a symmetric serration potential subjected to both unbiased thermal noise and spatially inhomogeneous three-level colored noise.It is found that the appearance of the absolute negative mobility depends on the parameters of nonequilibrium and thermal noises such as amplitude,temperature,switching rate.[8]In addition,the absolute negative mobility can be induced by the spatial asymmetry in the shape of the transported particles,[4]white Poissonian noise,[6]the colored thermal fl uctuations.[5]

The absolute negative mobility has been experimentally detected and theoretically studied in pmodulation-doped multiple quantum wells,[9]semiconductor superlattices,[10]and tunnel junction in superconductor devices.[11]In addition,negative conductances or even absolute negative conductances have been theoretically interpreted in the Josephson junctions[12−15]according to electric transportation.

However,in contrast to the regular potential,the shape of the substrate potential,which deviates from the standard one is more common in the real physical systems.The deformation of the potential may have a great in fl uence on the transport characteristics of the particle.In the physical situations,application of standard Frenkel-Kontorova(FK)model could be very restricted,and real physical systems could not be“exactly” described by standard models.[16]For wider generality,Remoissenet and Peyrard[17−18]obtained in a control manner by an adequate choice of parameters rich variety of deformable potentials related to the physical systems such as Josephson junctions,charge-density wave condensates,and crystals with dislocations,these deformable potentials allow the modeling of many speci fic physical situations without employing perturbation methods.Therefore,it is necessary to study the in fl uence of the deformation of the potential on average particle velocity.In this paper,we extend the previous work from standard sinusoidal potentials to the asymmetric deformable potentials.We will focus on how the deformation of the potential affects the directed transport.Since the inertial of the particle affects the anomalous transport feature,we will discuss the underdamped motion of a Brownian particle.

2 Model and Methods

We consider underdamped dynamics of a Brownian particle in the presence of the one-dimensional asymmetric deformable potential.[17,19]The particle is subjected to both an unbiased time-periodic external forceAcos(Ωt)and a constant forceF.Its dynamic can be described by the following inertial Langevin equation:[2,20]

The dot and the prime denote the differentiation with respect to timetand the Brownian particle’s coordinatex,respectively.mindicates the mass of the particle.Γ is the friction factor.Aand Ω denote the amplitude and the angular frequency of the ac driving force,respectively.kBis the Boltzmann constant andTis the thermodynamics temperature.Thermal equilibrium fl uctuations owing to the coupling of the particle with the environment are modeled by the Gaussian white noiseξ(t),which satis fies with the following relation

The asymmetric deformable potential can be given by[17,19]

where∆Uis the height of the potential andris the deformable parameter in the range from−1 to+1.Whenr=0,the potential becomes to the standard sinusoidal one,and forit is an asymmetric deformable potential,which has a static barrier height and two inequivalent successive wells with a fl at and sharp bottom,respectively.The deformation of the potential increases with the increasing ofThe period of the potential isL.Equation(1)can be rewritten in dimensionless form:

Here we will use Brownian dynamic simulations to study the transport of the particle.The average velocityof the particle can be obtained from the following formula:

wheret0is the initial time.

3 Results and Discussion

During the numerical simulations,we set the step time∆tto be 0.001 and the total integration time to be more than 107.Unless otherwise noted,our simulations are under the parameter sets:γ=0.9,ω=4.9,a=4.2,∆U=1.0,andD0=0.001.

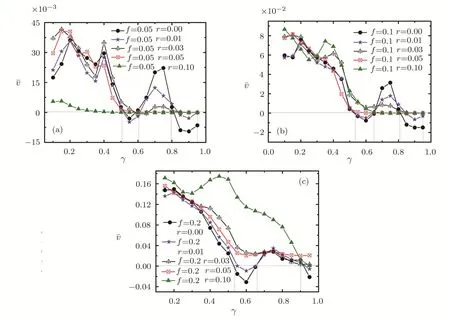
Figure 1 shows the average velocityas a function of the static forceffor different values ofr.When the forcefandrare both small,the absolute negative mobility is presented.However,whenfincreases,the current shows a reversal,which means the absolute negative mobility disappears.When the forcefis larger than 0.175,the average velocity¯vis always positive and increases with the increasing off.It is noted that there are two current reversals presented forr=0.015.Namely,the average velocity¯vis firstly positive,then negative,and finally positive.From Fig.1,we can also obtain that the behaviors of¯vare very different for the different values ofr.Whenr=0,it is equivalent to the Brownian particle moving in the simply sinusoidal potential,the average velocity is negative forf<0.17.It means that the absolute negative mobility can be observed in the range off

Whenris not equal to zero,the deformable potential has two inequivalent wells with the fl at and sharp bottoms.When the particle stays in the fl at well,it can easily pass through the barriers although the force acting on it is very small.When the particle stays in the sharp well,although the acting force is very large,it is also hard for the particle to pass through the barriers.Therefore,the fl at well is bene ficial to the particle’s transport while the sharp well impede the particle’s transport.Whenrincreases but it is smaller,the effect of the fl at well on particle’s transport is larger than that of the sharp one.At this time,the fl at well dominates the particle’s transport and the absolute negative mobility is suppressed.On the further increasingr,the particle in the sharp well is trapped more strongly.When the force is not large enough,the particle can not pass through the potential,so the average velocitytends to zero.However,when the force is large enough,the transport of the particle is dominated by the static force,so the average velocityincreases with the increasing of the force.

Fig.1(Color online)Average velocity as a function of the static force f for different values of r.(a)0≤r≤0.013,(b)0.015≤r≤0.017,(c)r≥0.03.

Fig.2(Color online)Average velocity as a function of the noise intensity D0for different values of r and f.(a)f=0.05,(b)f=0.1,(c)f=0.2.

In Fig.2,we study the average velocityversus the noise intensityD0for different values ofrandf.From Figs.2(a)and 2(b),we can see the absolute negative mobility is presented whenD0andrare both small.WhenD0increases,the current shows a reversal from negative to positive and the average velocityincreases with the increasing ofD0.In addition,there is a small fl uctuation in the range of 0.1≤D0≤1.We also find that the potential deformation has stronger in fl uences on the absolute negative mobility.Whenrincreases,the absolute negative mobility is suppressed.Whenr≥0.03,the absolute negative mobility disappears and the average velocityis firstly equal to zero then increases with theD0increasing(Figs.2(a)and 2(b)).These results denote that the potential deformation affects the absolute negative mobility.In these cases,whenD0→0,the particle cannot pass across the barrier of the potential,so there is no net current.WhenD0increases from zero but is still small.At the same time,forr≤0.01,the probability of the particle in the fl at well is larger than in the sharp well and the particle can pass across the potential barrier.So the average velocity is not zero and the absolute negative mobility presents.With the increasing ofD0,the particle can jump freely between the fl at well and sharp well,so the average velocity goes to zero,reverses its direction,and increases monotonically to a certain value.It should be noted that the above phenomena occur when the force is small.From Fig.2(c),we can find the average velocity is always positive when the force is equal to 0.2.It indicates that the large force can drive the particle to move in its direction.

Fig.3(Color online)Average velocity as a function of the friction coefficient γ for different values of r and f.(a)f=0.05,(b)f=0.1,(c)f=0.2.

It is well known that the system is in underdamped state when the friction coefficientγis small.The system will move with the periodic oscillation and the amplitude of the oscillation logarithmically decreases with the time increasing.However,whenγis large enough,the system is in overdamped state and it will slowly move to the equilibrium position without any oscillation.In Fig.3,we display the average velocityas a function of the friction coefficientγfor different values ofrandf.We can find that the behavior of the average velocity(r̸=0.1)shows the oscillation motion and presents several peaks as what the underdamped system transport curve shows.However,whenr=0.1,the behavior ofshows the same as the overdamped system transport(Fig.3(a)).Very interestingly,contrary to Figs.1 and 2,the average velocity(r=0 andr=0.01)shows three reversals with the increasing ofγ,which means that there are two intervals of the absolute negative mobility.Forr≥0.03,the absolute negative mobility disappears and the average velocity is equal to zero or larger than zero.In addition,the average velocity behaviors are also different from Fig.2 forr=0 andr=0.01.The absolute negative mobility always presents when the force is equal to 0.2.The forcefonly affects the amplitude ofand the absolute negative mobility is determined byrandγ.

4 Concluding Remarks

In summary,we numerically study the transport of a particle in a one-dimensional asymmetric deformable potential.It is found that the competition between the force and the deformation of the potential can result in the current reversals and the absolute negative mobility suppressed.Remarkably,when the deformable parameterr=0.015,there are two current reversals presenting.Whenr≤0.016,the absolute negative mobility is suppressed with the increasing ofr.Whenr>0.016,the absolute negative mobility disappears.When the noise intensity,the force,and the potential deformation are small,the absolute negative mobility and current reversals present,whereas the absolute negative mobility disappears when both the force and the potential deformation are large.Very interestingly,the average velocity behaviors as a function of the friction coefficient for different values ofrandfare very different.These show the oscillation motion and three reversals with the increasing ofγ,which means that there exists two intervals of the absolute negative mobility whenris small.Therefore,we can obtain the current reversals and control the particle’s transport direction by changing the potential deformation.The results we have presented may be another way to manipulate the transport of particles in complex environments.Furthermore,we expect our results can help people develop a new route to control particle systems based on the underdamped dynamics.

[1]R.Eichhorn,P.Reimann,and P.Hänggi,Phys.Rev.Lett.88(2002)190601.

[2]L.Machura,M.Kostur,P.Talkner,et al.,Phys.Rev.Lett.98(2007)040601.

[3]B.Q.Ai and L.G.Liu,Phys.Rev.E 76(2007)042103.

[4]P.Hänggi,F.Marchesoni,S.Savelev,and G.Schmid,Phys.Rev.E 82(2010)041121.

[5]M.Kostur,J. Luczka,and P.Hänggi,Phys.Rev.E 80(2009)051121.

[6]J.Spiechowicz,J. Luczka,and P.Hänggi,J.Stat.Mech.(2013)P02044.

[7]P.K.Ghosh,P.Hänggi,F.Marchesoni,and F.Nori,Phys.Rev.E 89(2014)062115.

[8]A.Haljas,R.Mankin,A.Sauga,et al.,Phys.Rev.E 70(2004)041107.

[9]R.A.Höpfel,J.Shah,P.A.Wol ff,and A.C.Gossard,Phys.Rev.Lett.56(1986)2736.

[10]B.J.Keay,S.Zeuner,S.J.Allen Jr,et al.,Phys.Rev.Lett.75(1995)4102.

[11]M.E.Gershenzon and M.I.Faleǐ,Zh.Eksp.Teor.Fiz.94(1988)303;Sov.Phys.JETP 67(1988)389;Pis’ma,Zh.Eksp.Teor.Fiz.44(1986)529;JETP Lett.44(1986)682.

[12]L.Machura,M.Kostur,J. Luczka,et al.,Physica E 42(2010)590.

[13]M.Kostur,L.Machura,P.Talkner,et al.,Phys.Rev.B 77(2008)104509.

[14]M.Kostur,L.Machura,J. Luczka,et al.,Acta Phys.Polon.B 39(2008)1115.

[15]J.Nagel,D.Speer,T.Gaber,et al.,Phys.Rev.Lett.100(2008)217001.

[16]B.Q.Ai and B.B.Hu,Phys.Rev.E 83(2011)011131.

[17]M.Remoissenet and M.Peyrard,Phys.Rev.B 29(1984)3153.

[18]M.Peyrard and M.Remoissenet,Phys.Rev.B 26(1982)2886.

[19]J.Tekic and B.Hu,Phys.Rev.E 81(2010)036604.

[20]P.Hänggi and H.Thomas,Phys.Rep.88(1982)207.