Thermally Radiative Rotating Magneto-Nano fl uid Flow over an Exponential Sheet with Heat Generation and Viscous Dissipation:A Comparative Study

M.Sagheer,M.Bilal,S.Hussain,and R.N.Ahmed

Department of Mathematics,Capital University of Science and Technology,Islamabad,Pakistan

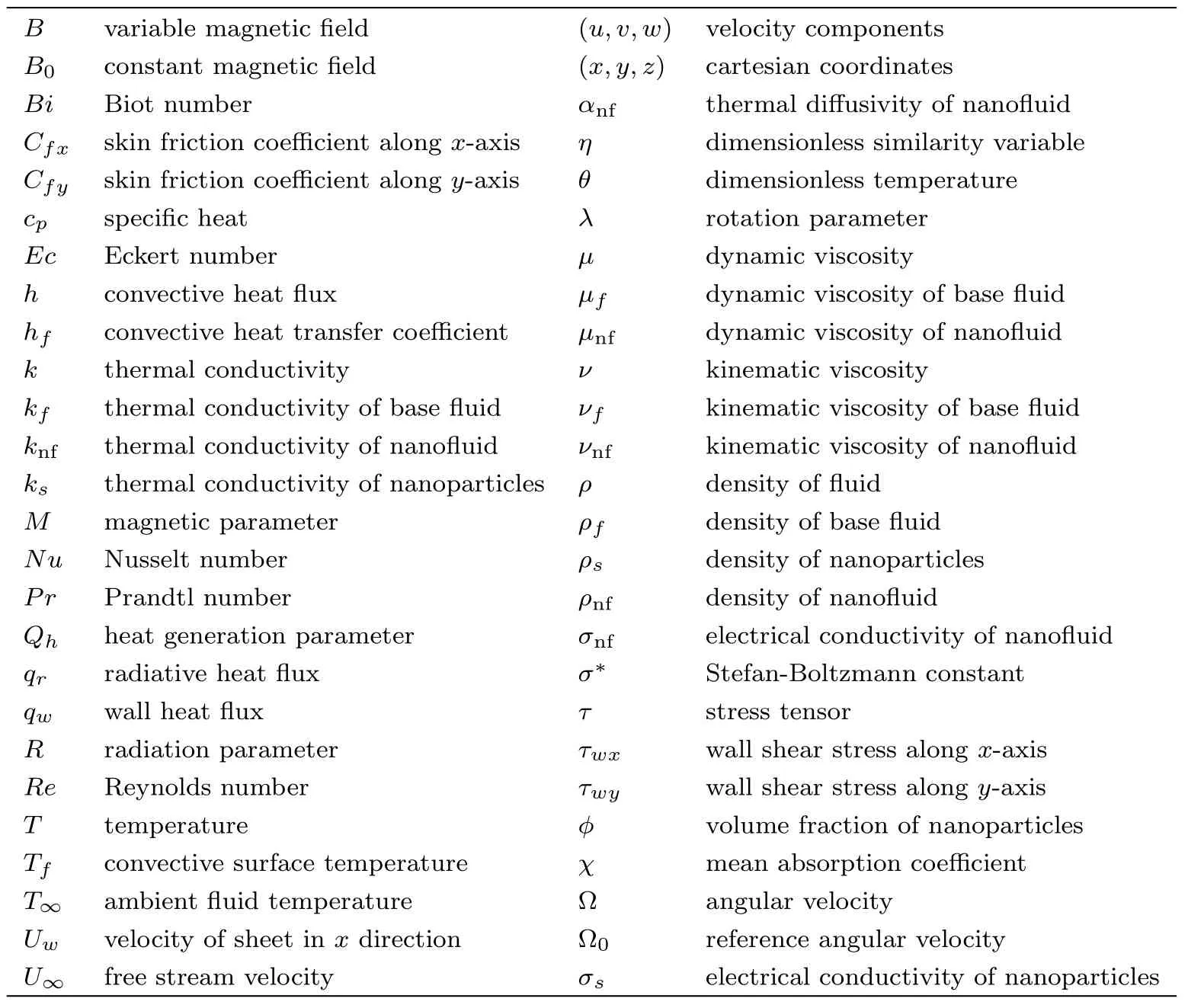
Nomenclature

?

1 Introduction

In the present fast growing and developing computer age,the transportation,communication,heavy mechanical industries,electronics industries and house hold appliances,all are running by some mechanical and electronic devices.Almost in all such devices,according to the requirements of devices,a system of cooling or heating is built-in,by which a fl uid fl ows through or around the device to prevent these devices from overheating or cooling down from certain temperature threshold.To meet the human requirements and demand of the market,it is essential that these devices work round the clock.To keep the devices at a constant temperature,the heat dissipated must be equal to the heat generated.The conventional fl uids with low thermal conductivity do not meet the temperature requirements of many mechanical and electronics devices,which results in poor performance of these devices and reduces their efficiency and working age.Therefore,it is imperative to improve the thermal conductivity of the conventional fl uids.

The conventional fl uids used for the transfer of heat energy were first time replaced by the nano fl uids by Choi[1]followed by many researchers.A nano fl uid is a mixture of nanoparticles in a conventional heat transfer fl uid.The nanoparticles(1–100 nm)in size are usually metals,metallic oxides,nano fibers,etc.Choi[1]experimentally found that the nanoparticles when added to the base fl uids,considerably improve the thermal conductivity of the base fl uid.Magyari and Keller[2]focused on the heat and mass transfer analysis in the boundary layer fl ow due to an exponentially continuous stretching sheet.Eastmanet al.[3]observed that the thermal conductivity of pure ethylene glycol is much increased when copper nanoparticles are added to it.Liet al.[4]investigated the MHD nano fl uid fl ow in a thin film through unsteady stretching sheet with additional effects of thermal radiation,heat generation,Brownian motion,and thermophoresis.They used theMATLABbuilt-in bvp4c solver to solve their ODEs.It is found form their investigation that temperature and nanoparticle concentration have opposite behavior for the thermophoresis parameter.Nadeemet al.[5]analyzed the in fl uence of nanoparticles on the two-dimensional fl ow of Maxwell nano fl uid over a stretching sheet for the heat and mass transfer effects.By applying the boundarylayer approximation,they also incorporated the effects of MHD and elasticity parameter.Sheikholeslamiet al.[6]presented an analysis focusing on the unsteady squeezing fl ow of electrically conducting nano fl uid using the homotopy perturbation method.Two phase simulation model for the nano fl uid is considered along with the magnetohydrodynamics effects.They concluded that the Nusselt number is a decreasing function of the squeezing parameter.Another useful contribution of Sheikholeslami and Ganji,[7]is a review work addressing both the single and the double phase models for the nano fl uids.They describe brie fl y the various attempts of different scientists on heat transfer of convective nano fl uids.It is further analyzed that while increasing the Reynolds number and Rayleigh number,the rate of heat transfer is increased.Sheikholeslamiet al.[8]discussed the thermal radiation on MHD free convection of Al2O3-water nano fl uid.Chopkaret al.[9]studied the effect of the size of the nanoparticles on the thermal conductivity of nano fl uid and found that the thermal conductivity decreases by increasing the size of the particles.In last half decade,many articles related to the nano fl uid dynamics are published in literature.[10−24]

A reasonable number of applications emphasizing the role of steady and unsteady rotating fl ows may be found in chemical and geophysical fl uid mechanics.These all are of applied nature like in the thermal power generating systems,food processing,the skins of high speed air crafts and in rotor stator systems.The pioneering work highlighting the rotating fl ow was done by Wang.[25]Takharet al.[26]discussed the effects of magnetohydrodynamic in a rotating fl ow.They concluded that the skin friction along thex-axis increases for the higher values of the magnetic parameter and has a reverse relation for they-axis skin friction coefficient.Zaimiet al.[27]applied the numerical technique to examine the rotating fl ow of viscoelastic fl uid.Turkyilmazoglu[28]applied the spectral numerical integration method for the problem related to the shrinking rotating disk with the effect of magnetohydrodynamic.Some recent attempts emphasizing the rotating fl ow can be found in Refs.[29–31].

During the study of nano fl uid,the thermal radiative properties of Newtonian and non-Newtonian fl uids for the heat transfer phenomenon have got much attention.Because of the insertion of the nanoparticles in the base fl uid,the thermal properties are enhanced which resultantly rises the temperature of the nano fl uids and for the higher temperature differences,the effects of the thermal radiation cannot be neglected.The operating systems performing the energy conversion at high temperature show a comparable effect of the thermal radiation.In other engineering and chemical processes such as solar water technology,fossil fuel combustion,astrophysical fl ows,hypersonic fl ights,gas turbines,space vehicles,nuclear reactors etc.,the effects of thermal radiations are quite phenomenal.Many researchers have considered the in fl uence of thermal radiation on the boundary layer fl ow of Newtonian and non-Newtonian fl uids.Mushtaqet al.[32]considered the nonlinear thermal radiation in the two-dimensional stagnation point fl ow with additional effects of Joule heating and viscous dissipation over a convectively heated surface.They deduced that both the temperature and its gradient are increasing functions of thermal radiation parameter.Pourmehranet al.[33]numerically investigated the MHD boundary layer fl ow of nano fl uid through convectively heated vertical stretching sheet.During the study,the in fl uence of thermal radiation and buoyancy effects got special attention.Pourmehran et al.considered three different types of base fl uid i.e.,pure water,ethylene glycol 30%and ethylene glycol 50%while the four types of nanoparticles i.e.,copper,silver,alumina,and titanium oxide.

Motivated by the above mentioned literature,the primary objective of the present study is to examine the effects of thermal radiation and viscous dissipation on heat transfer fl ow over a bi-directional convectively heated exponentially stretching sheet in the presence of transverse magnetic field and volumetric rate of heat generation.Five different nanoparticles(silver,copper,copper oxide,titanium oxide,alumina)are assumed to be suspended in the pure water.A detailed comparative study of these nano fl uids for the fl ow and heat transfer is presented and discussed graphically and numerically.Boundary layer approximations are used to govern the partial differential equations,which are then transformed to the ordinary differential equations with the help of transformations.The modeled problem is solved numerically by the shooting method using Runga-Kutta integration scheme of order 4.Effects of emerging parameters on velocity and temperature pro files are discussed in detail.Nusselt number and skin friction coefficient are also calculated.In the limiting case,the results are veri fied by reproducing the results of previously published article[34−35]

2 Mathematical Formulation

A laminar,incompressible and steady water-based electrically conducted nano fl uid fl ow over an exponentially bidirectional stretching sheet is considered.Sheet temperatureTfis controlled via convection by considering hot fl uid below it.The temperature faraway from the surface where its difference is negligible is known as the ambient temperature and is denoted byT∞.The fl uid is assumed to rotate with angular velocityalongz-axis having the coriolis effect.A transverse variable magnetic fieldis applied alongz-axis with the assumption of small Reynolds number,ignoring the induced magnetic field.The fl uid has internal volumetric rate of heat generationIn thexdirection,the velocity of the sheet is taken asas shown in Fig.1.

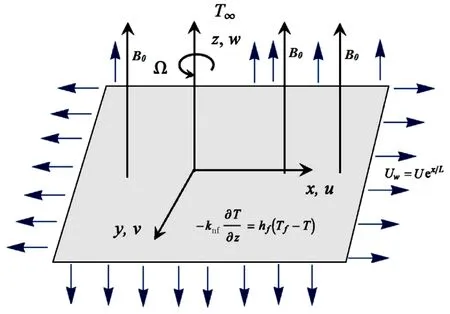
Fig.1 Geometry of the Problem.

Further the effects of the thermal radiation,Joule heating and viscous dissipation are considered in the formulation of energy equation.For the nano fl uid model,the Tiwari and Das model.[36]has been utilized.Applying the boundary layer by incorporating the Boussinesq approximations,the conservation equations of mass,momentum and energy in the mathematical form can be expressed as

In Table 1,the thermo-physical properties of different nanoparticles and pure water are shown.The following dimensionless variables are used to convert the system of the non-linear PDEs to the system of ODEs.

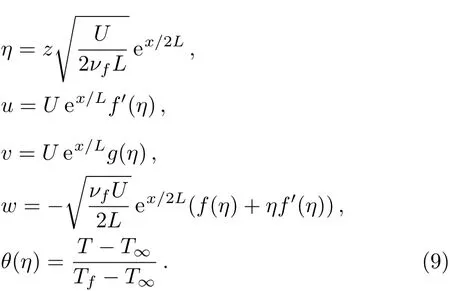
In Eq.(4),qris a radiative heat fl ux which is de fined as

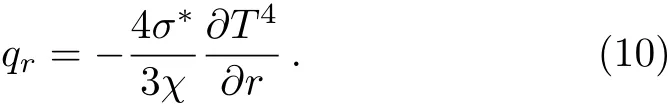
Furthermore,the temperature difference within the fl ow is assumed such thatT4may be expanded in a Taylor series.Hence,expandingT4aboutT∞and neglecting the higher order terms,we get

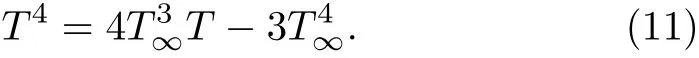
Using the similarity transformation de fined in Eq.(9),Eq.(1)is identically satis fied while Eqs.(2)–(5)are converted into the following nonlinear ordinary differential equations:

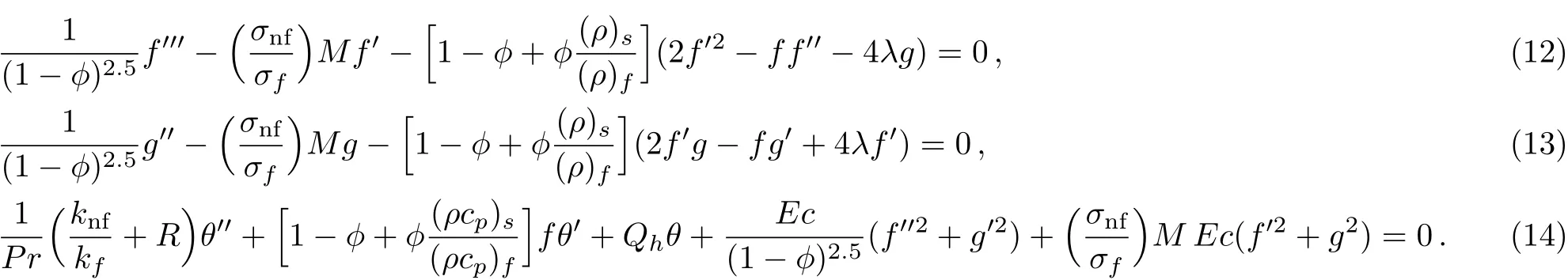
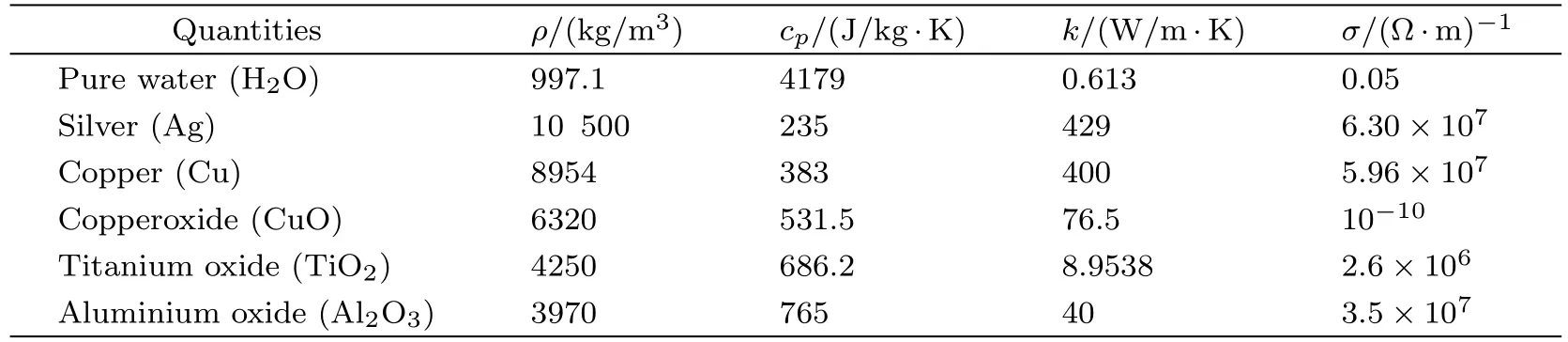
Table 1 Thermo-physical properties of H2O and nanoparticles.

The transformed boundary conditions are:

3 Solution Methodology

An efficient numerical technique,namely the shooting method has been employed to solve the transformed ordinary differential equations along with the boundary con-ditions for different values of the emerging parameters.While applying the shooting method,[42]first the higher order boundary value problem is converted to a system of first order initial value problem(IVP).During the conversion,fis denoted byy1,gbyy4andθbyy6.The missing initial conditions are supposed to beς1,ς2andς3.The converted first order IVP takes the following form

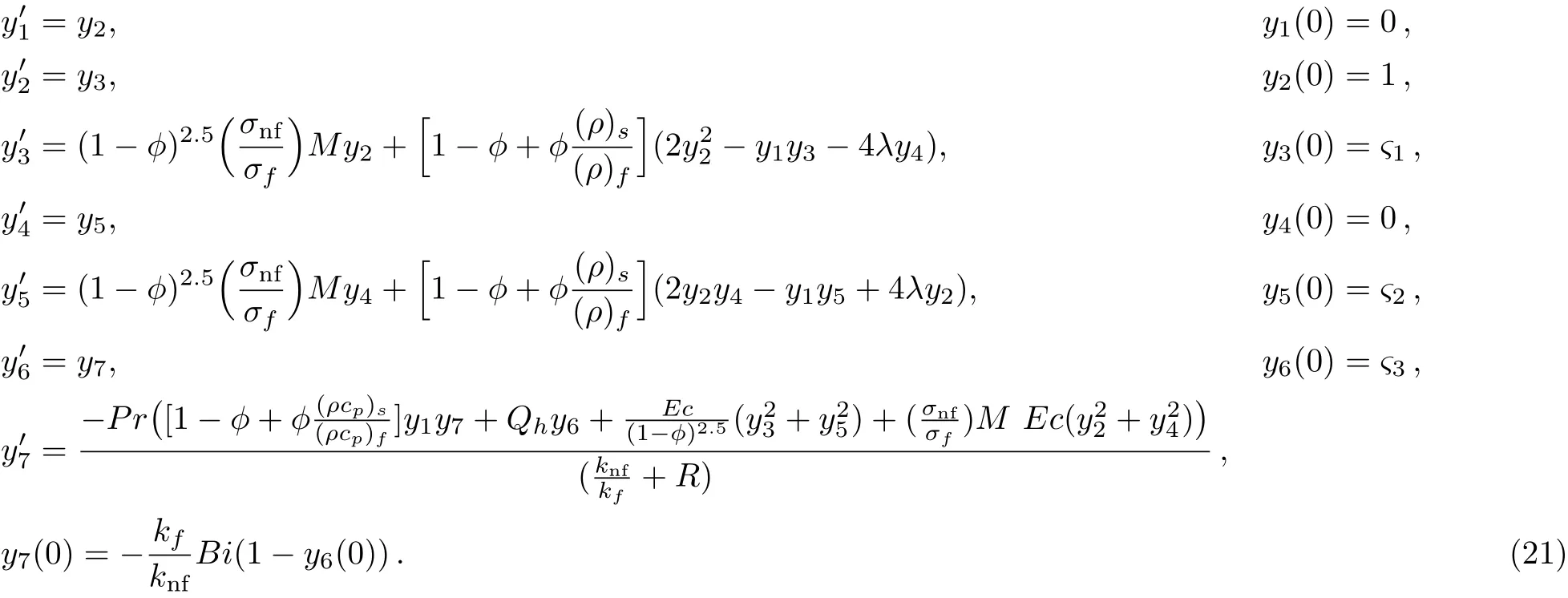
Fourth order Runge-Kutta method is utilized to solve this IVP.The re finement of initial guesses is carried out by the Newton’s method.Because the numerical solution cannot be computed on the unbounded domain[0,∞),a bounded domain[0,η∞]has been considered,whereη∞is an appropriate real number.After performing a number of computational experiments,η∞is set to 4,because there is no signi ficant variation in the results forη∞>4.The stoping criteria set for the Newton’s iterative process is

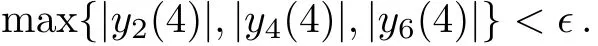
Throughout this article,ϵis chosen as 10−6.For the validation of theMATLABcode of the shooting method,it is affectively applied to reproduce the numerical results of Javedet al.[35]and Ahmad and Mustafa.[34]The successful comparison has been presented in Table 2.

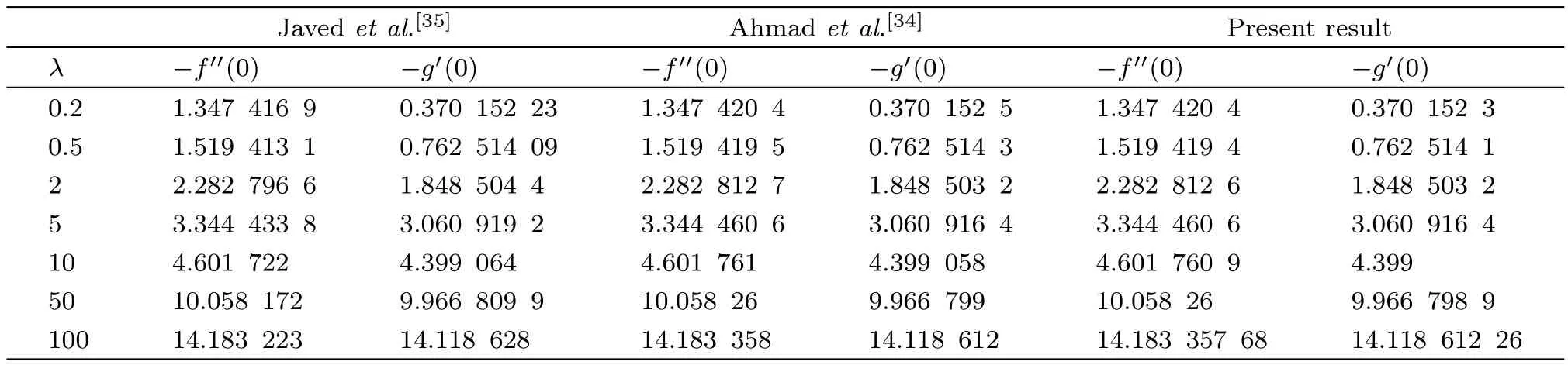
Table 2 Comparison of present results with those of Javed et al.[35]and Ahmad and Mustafa.[34]

4 Results and Discussions

In this section,we discuss the in fl uence of different parameters such as nanoparticles volume fractionϕ,rotational parameterλ,magnetic parameterM,thermal radiation parameterR,Eckert numberEc,heat generation/absorption parameterQhon the velocity,temperature,skin-friction and Nusselt number,both graphically and numerically in the tabular form.

In Table 3,the in fl uence of the nanoparticle volume fractionϕ,rotational parameterλand magnetic parameterMon the skin friction coefficient alongx-axis is presented for different nanoparticles.It is observed that due to the addition of more nanoparticles in the base fl uid,the skin-friction is enhanced.This enhancement is more rapid in Ag-H2O nano fl uid whereas in case of Al2O3-H2O,the increase in the skin-friction is less as compared to the other nanolfuids.Quite similar behavior is noticed for the rotational parameterλ.When the magnetic field is intensi fied along thez-axis,the skin-friction escalates along thex-axis due to the presence of the Lorentz force.Again,Ag-H2O nano fl uid has more frictional force as compared to the other nano fl uids.

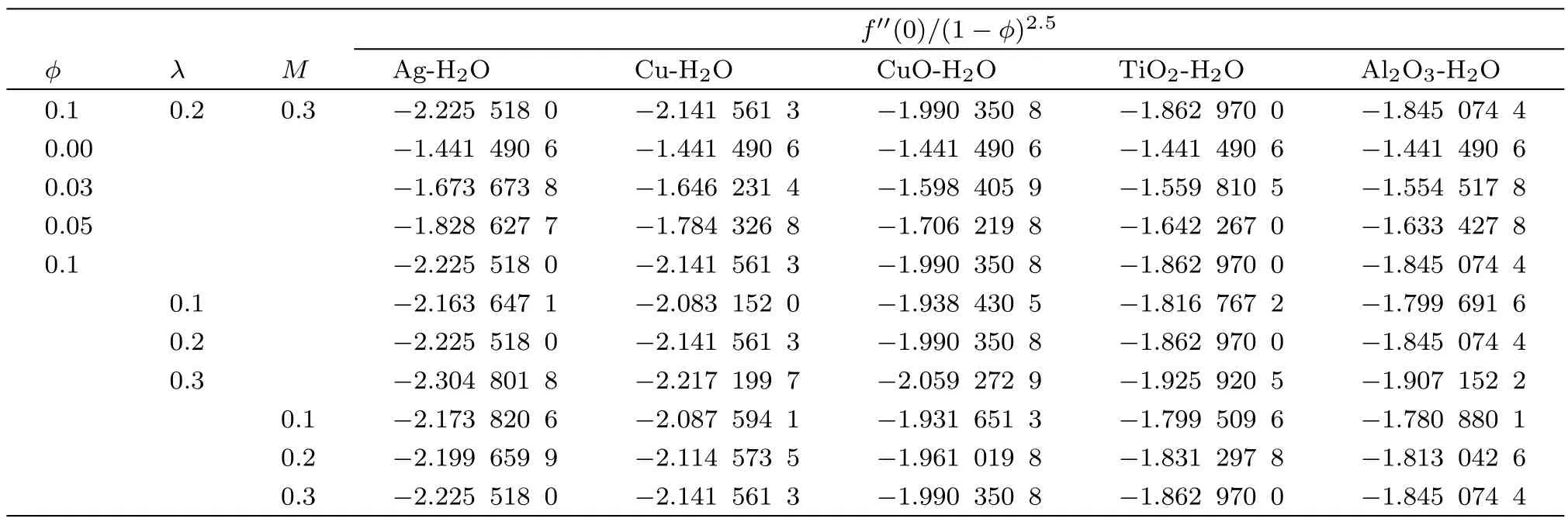
Table 3 Effect of ϕ,λ and M on the skin friction coefficient along x-axis when Qh=0.1,Bi=0.6,Pr=6.2,n=3.0,R=0.2,Ec=0.01.

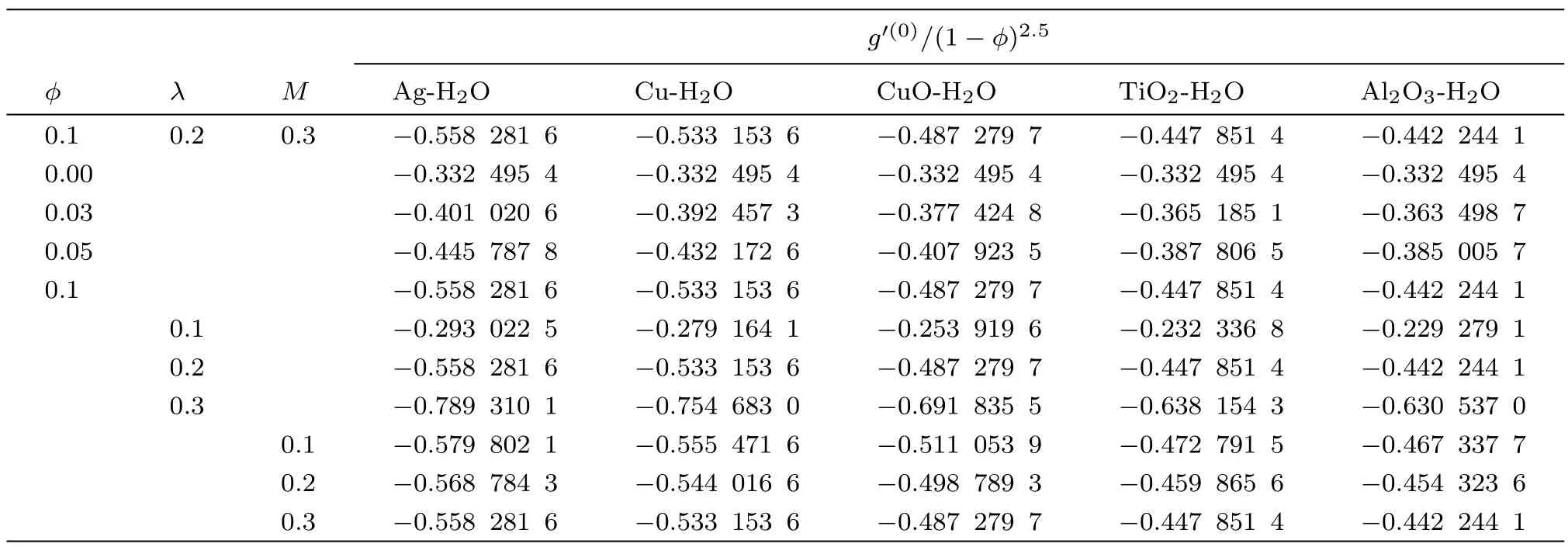
Table 4 Numerical values of skin friction coefficient along y-axis for different values of parameters when Qh=0.1,R=0.2,Ec=0.01.

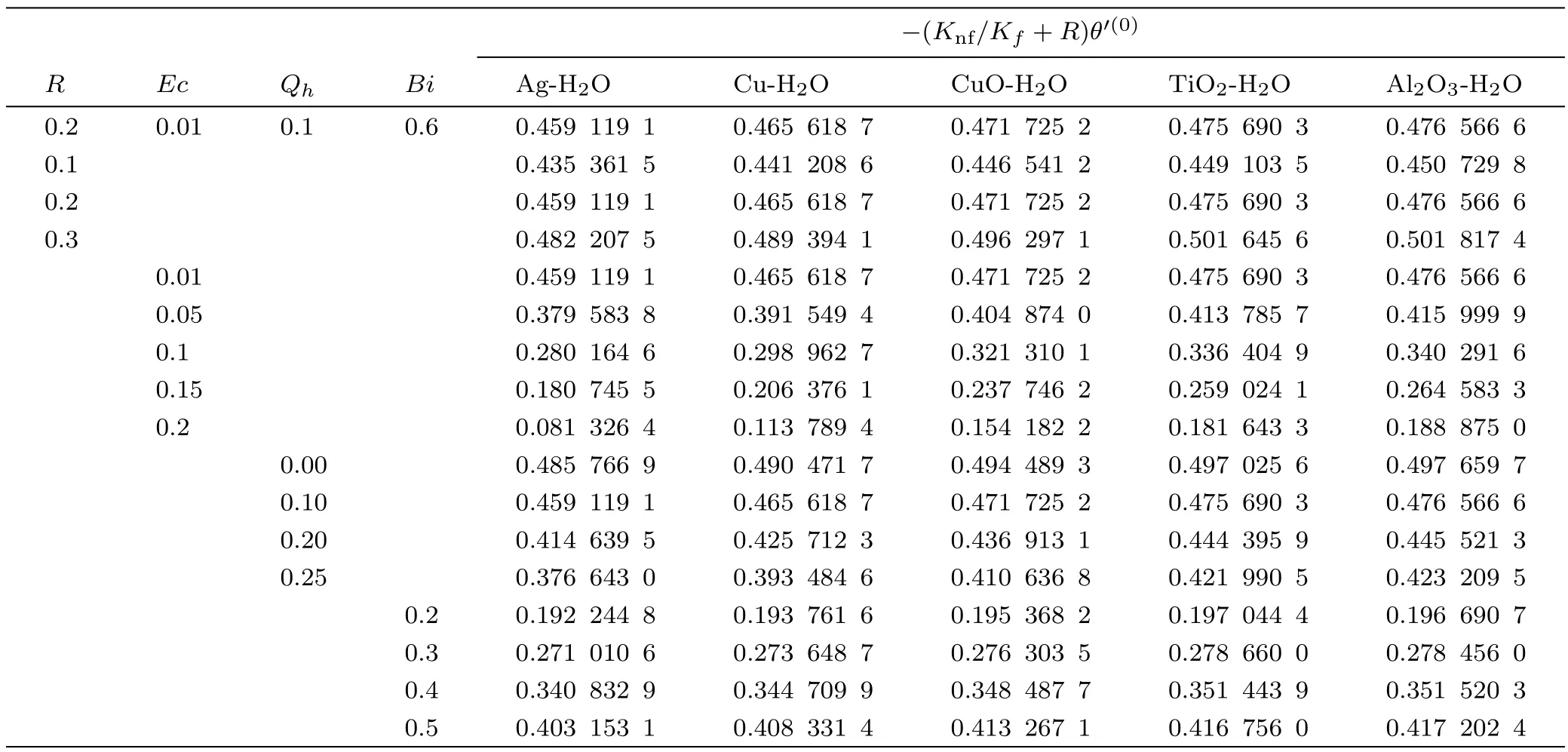
Table 5 Numerical values of local Nusselt for different values of parameters when ϕ =0.01,λ =0.2,M=0.3.

Table 3 shows the effect of variation of nanoparticles volume fractionϕ,rotational parameterλ,and magnetic parameterMon the skin friction coefficient alongyaxis. From the table,it is highlighted that fractional force between the fl uid and the solid surface in theydirection is enhanced when the nanoparticles volume fraction is increased.However this increase in skin friction is very small. Again it is observed that Al2O3water base nano fl luid has least increase when compared with the other nano fl uids.By escalating the angular velocity of the nanoparticles,the skin friction rises along they-axis.The effect of magnetic fieldMon the skin friction along they-axis is quite similar as already shown in Table 3.By enhancing the magnetic parameter,the surface fractional force also increased.

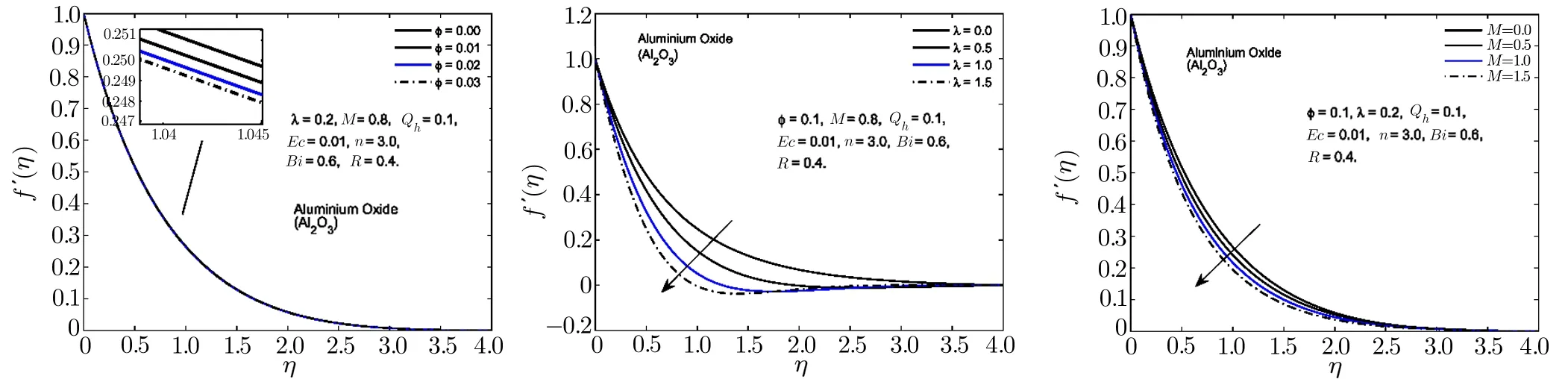
Fig.2 In fl uence of ϕ,λ,and M on f′(η)for Al2O3-H2O nano fl uid.

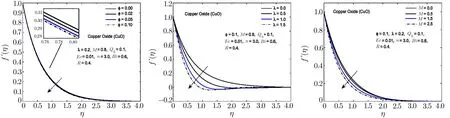
Fig.3 In fl uence of ϕ, λ,and M on f′(η)for CuO-H2O nano fl uid.

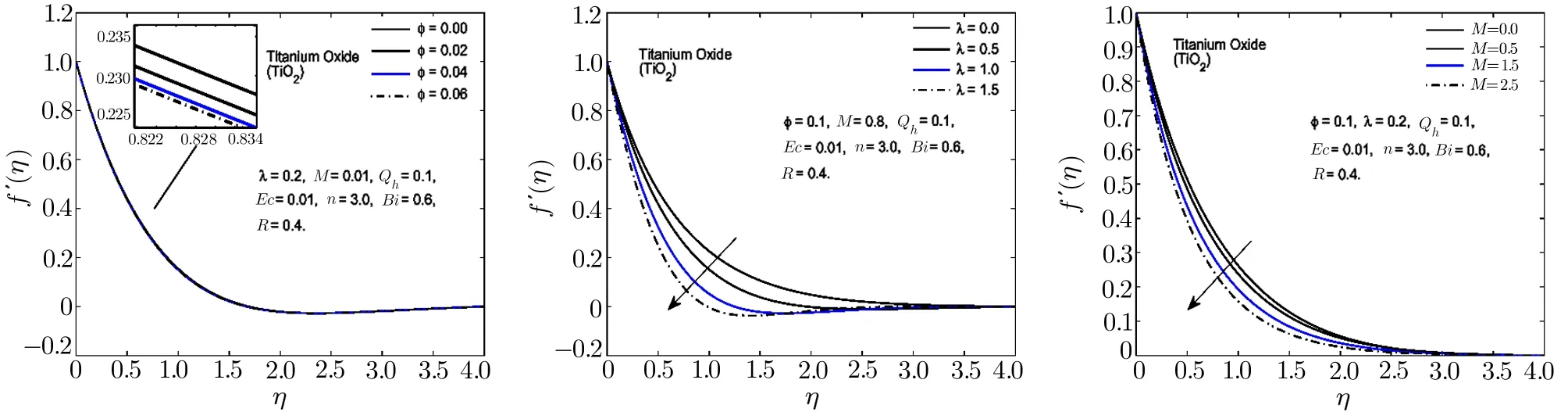
Fig.4 In fl uence of ϕ, λ and M on f′(η)for TiO2-H2O nano fl uid.

The effect of thermal radiation parameterR,Eckert numberEc,heat generation/absorption parameterQhand Biot number on Nusselt number is shown in Table 5.From this table,it is observed that these parameters have increasing effect on the Nusselt number.The comparison among different nanoparticles exhibits that Al2O3-H2O nano fl uid possesses the highest value of Nusselt number for thermal radiation parameter.It is also perceived that Ag-H2O nano fl uid has more heat transfer rate as compared to the other nano fl uids for the increasing values of Eckert number and heat generation/absorption parameterQh.Nusselt number is also enhanced for the higher values of the Biot numberBi.It happens because for the higher values of the Biot number,a stronger convection is produced which causes higher rate of change in the temperature.

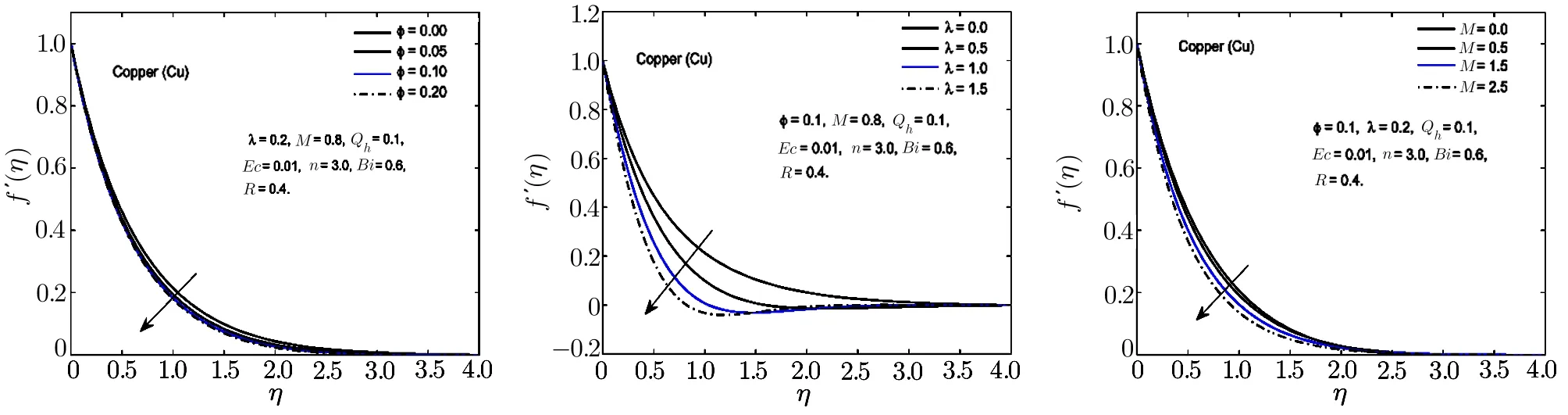
Fig.5 In fl uence of ϕ,λ and M on f′(η)for Cu-H2O nano fl uid.

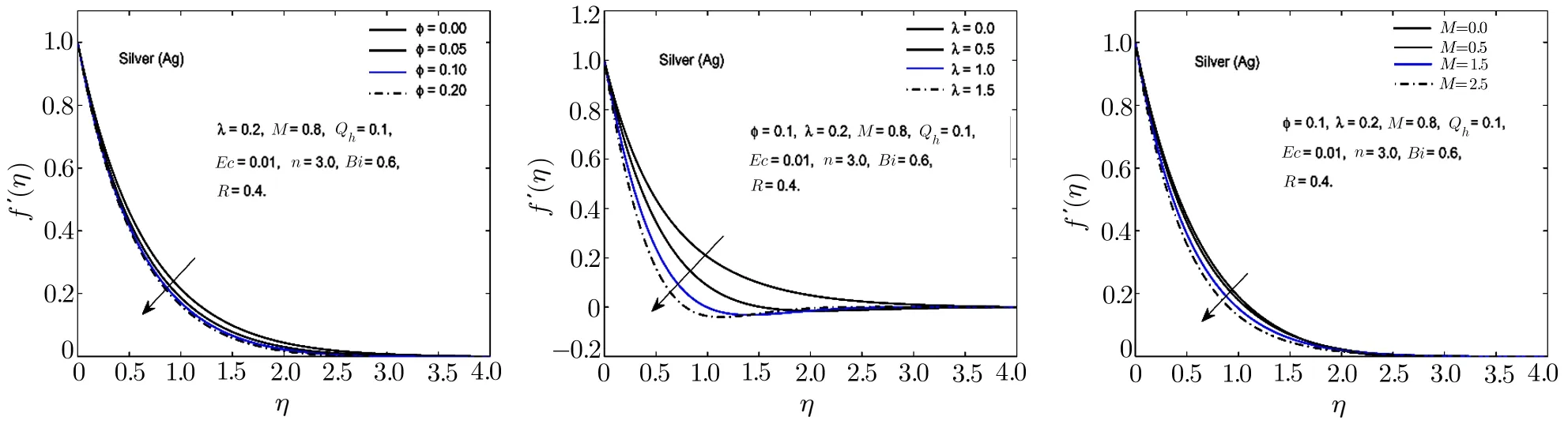
Fig.6 In fl uence of ϕ,λ and M on f′(η)for Ag-H2O nano fl uid.

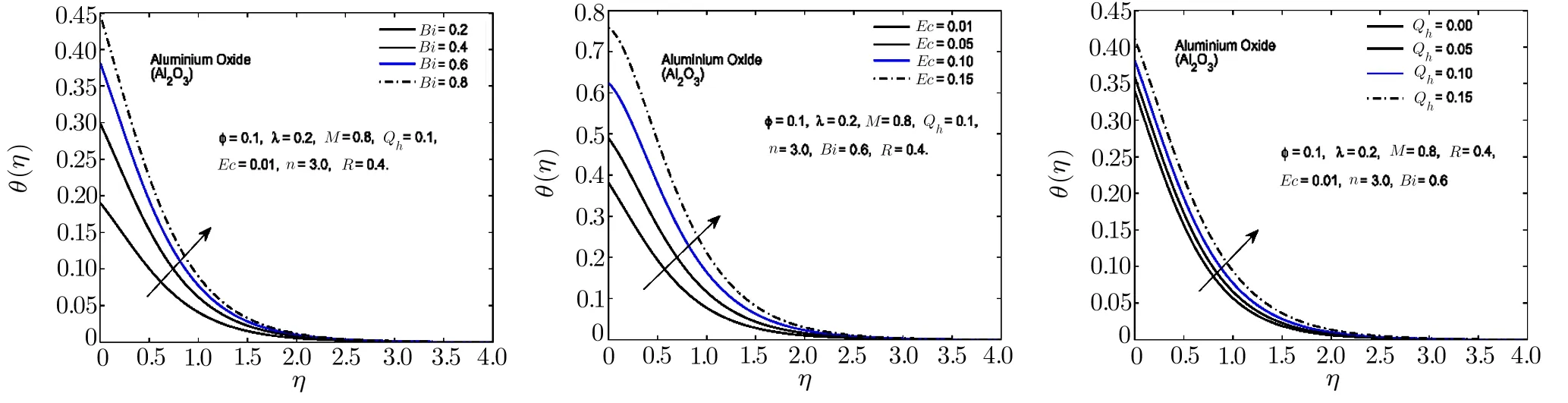
Fig.7 In fl uence of Bi,Ec and Qhon θ(η)for Al2O3-H2O nano fl uid.

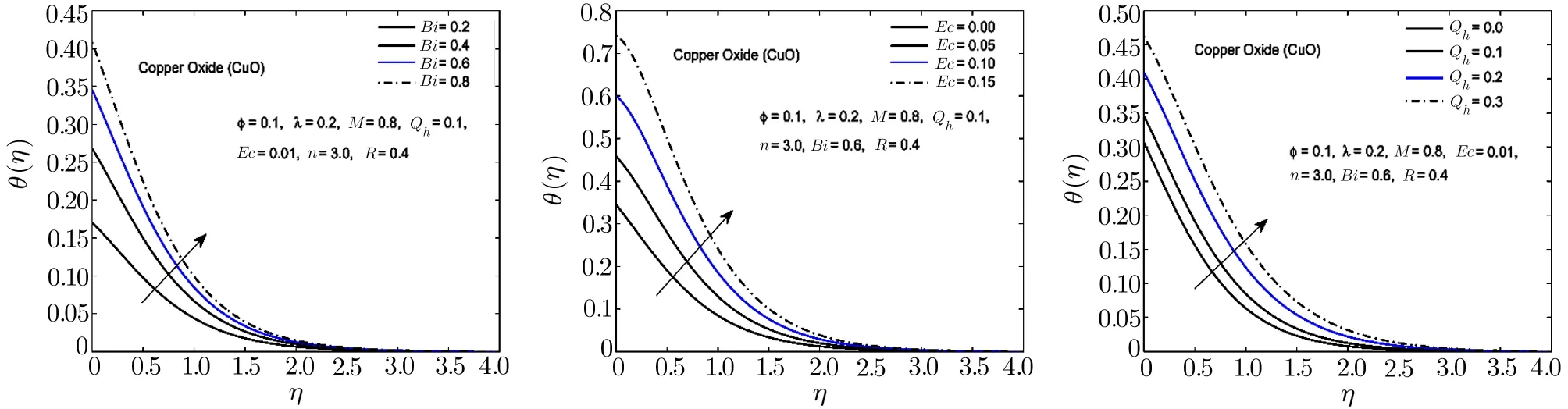
Fig.8 In fl uence of Bi,Ec and Qhon θ(η)for CuO-H2O nano fl uid.

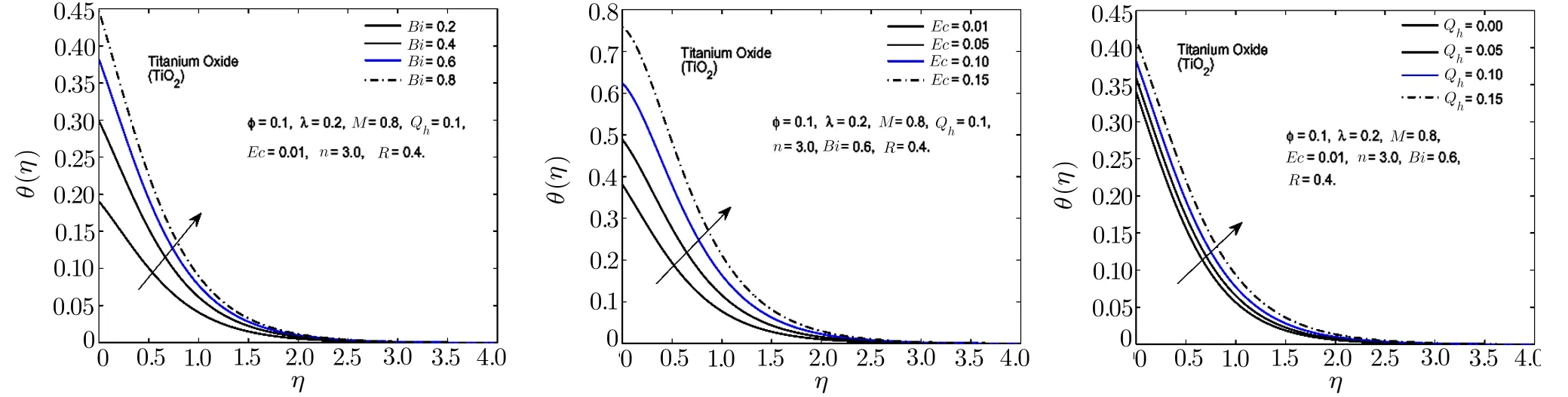
Fig.9 In fl uence of Bi,Ec and Qhon θ(η)for TiO2-H2O nano fl uid.

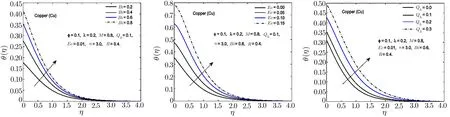
Fig.10 In fl uence of Bi,Ec and Qhon θ(η)for Cu-H2O nano fl uid.

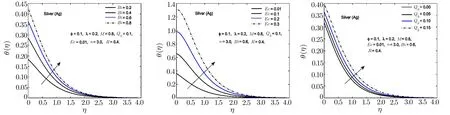
Fig.11 In fl uence of Bi,Ec and Qhon θ(η)for Ag-H2O nano fl uid.

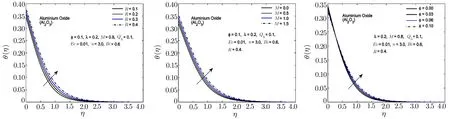
Fig.12 In fl uence of R,M and ϕ on θ(η)for Al2O3-H2O nano fl uid.

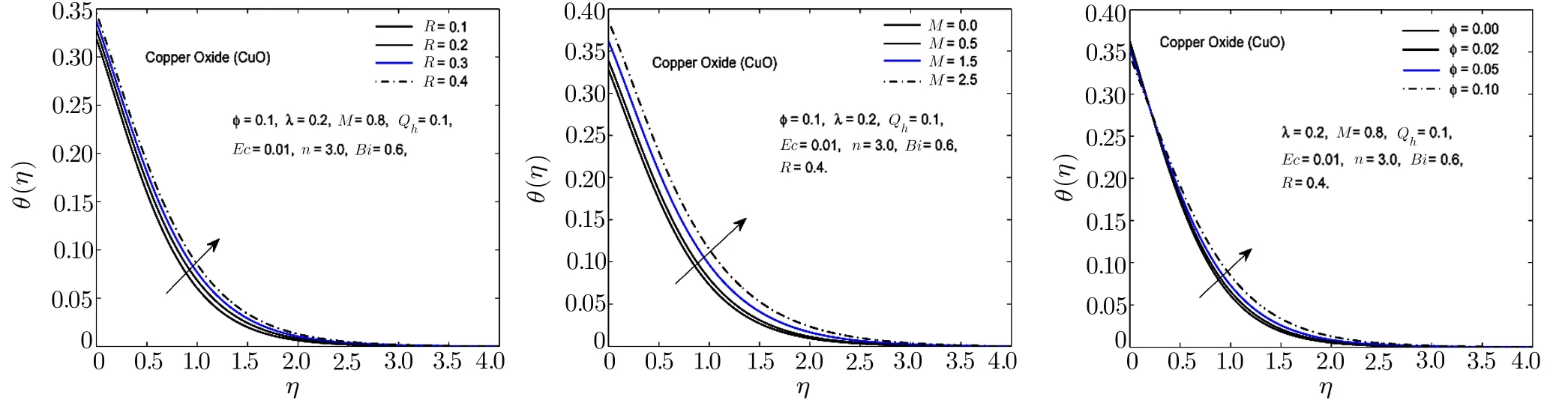
Fig.13 In fl uence of R,M and ϕ on θ(η)for CuO-H2O nano fl uid.

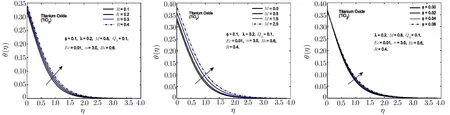
Fig.14 In fl uence of R,M and ϕ on θ(η)for TiO2-H2O nano fl uid.

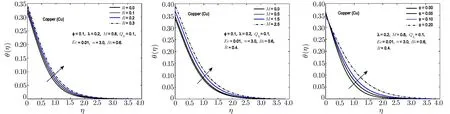
Fig.15 In fl uence of R,M and ϕ on θ(η)for Cu-H2O nano fl uid.

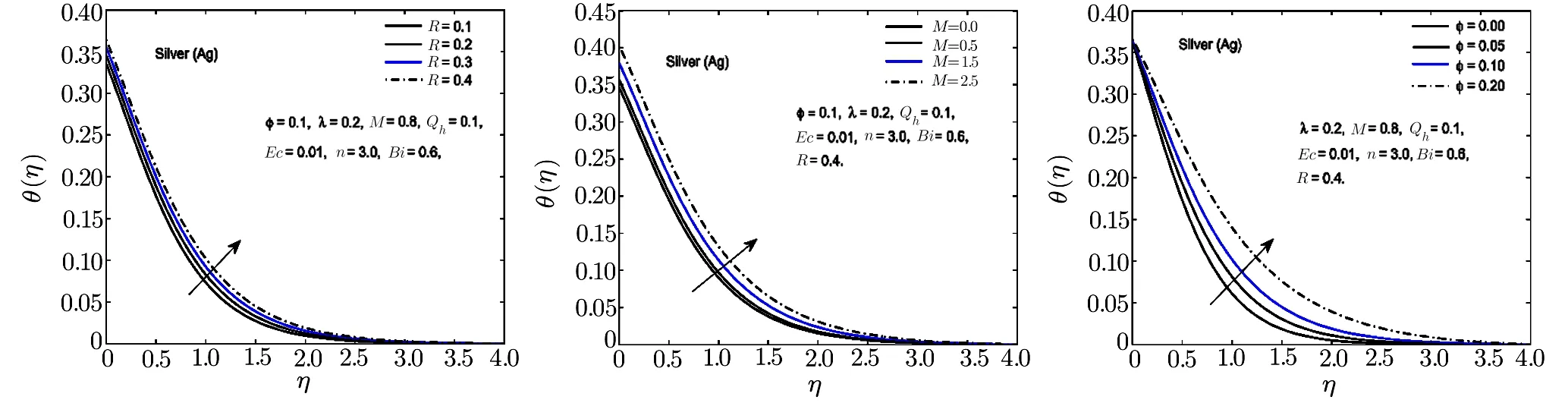
Fig.16 In fl uence of R,M and ϕ on θ(η)for Ag-H2O nano fl uid.

To visualize the effect of different physical parameters on the velocityf′(η)and the temperature pro fileθ(η),Figs.2–6 are plotted.In Figs.2–6,the effects of nanoparticle volume fractionϕ,rotational parameterλand magnetic parameterMon the velocity pro file for alumina,copper oxide,titanium oxide,copper and silver based nano fl uids are displayed.For all the nano fl uids,it is observed that the velocity as well as the boundary layer thickness of the nano fl uid decreases when the quantity of the nanoparticles in the base fl uid is increased.Velocity distribution is dominant at the surface of the sheet.The effect of rotational parameterλwhich is the associated with the angular velocity of the fl uid,on velocity pro file is displayed in Figs.2–6.From these figures,it is noticed that the velocity pro file and its momentum boundary layer thickness is reduced for the increasing values ofλ.Hence,the rotational effects resist the fl uid fl ow in thex-direction.For higher values of rotational parameter,the velocity becomes negative in some part of the boundary layer thickness and an interesting phenomenon of oscillatory decaying pro file are also observed.The Lorentz forces,which are resistive in nature are produced when the magnetic field is applied across the fl uid fl ow.These forces are responsible for the reduction in the fl uid particle’s motion for the higher values of magnetic parameterM.Hence for all the nano fl uids,the speed of the fl uid decreases for the increasing values of magnetic parameter.

To observe the effect of the variation in the Biot numberBi,Eckert numberEc,and heat generation parameterQhon the temperature distribution Figs.7–11 are plotted.It is observed that the higher values of the Biot number escalate the temperature distribution and the thermal boundary layer thickness.The same observation is preserved for all the nano fl uids.The strength of the convected heating is signi fied for the higher values of the Biot number which resultantly rise the temperature distribution.The temperature is enhanced when the Eckert number is increased.Eckert number appears in the energy equation because of the consideration of the viscous dissipation effects in the fl uid motion.It is inversely proportional to the difference between the fl uid temperature on the surface and the ambient temperature.An increase in the Eckert number means there is a slight temperature difference between the surface and the thermal boundary layer and hence the rate of heat transfer is reduced.This reduction in heat transfer rate leads to escalate the temperature of the nano fl uid as shown in Figs.7–11.The effect of heat generation parameterQhis also displayed in the same figures.It is quite obvious that if heat is generated from any external or internal source the temperature of the fl uid is increased.In Figs.12–16,the in fl uence of the thermal radiation parameterR,magnetic parameterMand nanoparticle volume fractionϕis displayed for the temperature distribution.Higher values of thermal radiation produces more heat in the working fl uid which rises the temperature and the thermal boundary layer thickness of the nano fl uid as shown in these figures.By increasing the magnetic field across the fl uid,the resistive forces are enhanced.Temperature is increased due to these resistive forces.Lastly,by inserting the more quantity of nanopartices in the base fl uid,the thermal properties of the fl uid go up and hence the temperature of the fl uid is increased.

5 Concluding Remarks

This article encompasses the three-dimensional MHD rotating fl ow of electrically conducting nano fl uid over an exponentially stretching sheet.The effect of heat generation,viscous dissipation and thermal radiation for five different nanoparticles is analyzed graphically and numerically.The main findings of the investigation are as follows.

•Al2O3-H2O nano fl uid has more capacity to transfer heat as compared to the other discussed nano fl uids when the thermal radiation is enhanced.

•The skin friction coefficient is maximum for Ag-H2O nano fl uid.

•An increase in the Eckert numberEcand the heat generation parameterQhreduces the Nusselt number.This reduction in the heat transfer rate is much lower for Ag-H2O nano fl uid.

•The velocity pro file diminishes for increasing values of the magnetic parameterM.

•Ag-H2O and Cu-H2O nano fl uids have greater values of the Nusselt number as compared to Al2O3-H2O and TiO2-H2O nano fl uids.

[1]S.U.S.Choi,ASME Int.Mech.Engr.Cong.Exp.78(1995)99.

[2]E.Magyari and B.Keller,J.Phys.D 32(1999)577.

[3]J.A.Eastman,S.U.S.Choi,S.Li,et al.,Appl.Phys.Let.78(2001)718.

[4]J.Li,L.Liu,L.Zheng,and B.B.Mohsin,J.Taiwan Inst.Chem.Engr.67(2016)226.

[5]S.Nadeem,R.U.Haq,and Z.H.Khan,J.Taiwan Inst.Chem.Engr.45(2014)121.

[6]M.Sheikholeslami,M.Hatami,and G.Domairry,J.Taiwan Inst.Chem.Engr.46(2015)43.

[7]M.Sheikholeslami and D.D.Ganji,J.Taiwan Inst.Chem.Engr.65(2016)43.

[8]M.Sheikholeslami,T.Hayat,and A.Alsaedi,Int.J.Heat Mass Transfer 96(2016)513.

[9]M.Chopkar,S.Sudarshan,P.K.Das,and I.Manna,Metall.Matter.Trans.A 39(2009)1535.

[10]M.Ramzan and M.Bilal,PLoS ONE 10(2015)e0124929.

[11]M.Ramzan and M.Bilal,J.Mol.Liq.215(2016)212.

[12]M.Bilal,M.Sagheer,and S.Hussain,Alex.Engr.J.,doi.org/10.1016/j.aej.2017.03.039,(2017).

[13]M.Sheikholeslami and S.A.Shehzad,Int.J.Heat Mass Transfer 109(2017)82.

[14]M.Bilal,S.Hussain,and M.Sagheer,Bull.Po.Acad.Sci.Tech.Sci.65(2017)383.

[15]M.Sheikholeslami and S.A.Shehzad,Int.J.Heat Mass Transfer 113(2017)796.

[16]M.Sheikholeslami,T.Hayat,and A.Alsaedi,Int.J.Heat Mass Transfer 108(2017)1870.

[17]M.Sheikholeslami and M.M.Bhatti,Int.J.Heat Mass Transfer 109(2017)115.

[18]M.Sheikholeslami and H.B.Rokni,Int.J.Heat Mass Transfer 107(2017)288.

[19]M.Sheikholeslami and M.M.Bhatti,Int.J.Heat Mass Transfer 111(2017)1039.

[20]M.Sheikholeslami and M.K.Sadoughi,Int.J.Heat Mass Transfer 116(2018)909.

[21]M.Sheikholeslami and M.M.Bhatti,Int.J.Heat Mass Transfer 111(2017)1039.

[22]M.Sheikholeslami,Phys.B 516(2017)55.

[23]M.Sheikholeslami,Eur.Phys.J.Plus.132(2017)55.

[24]M.Sheikholeslami and H.B.Rokni,Int.J.Heat Mass Transfer 115(2017)1203.

[25]C.Y.Wang,Zeitschrift für angewandte Math-ematik und Physik ZAMP 39(1988)177.

[26]H.S.Takhar,A.J.Chamkha,and G.Nath,Int.J.Therm.Sci.42(2003)23.

[27]K.Zaimi,A.Ishak,and I.Pop,Appl.Math.Mech.34(2013)945.

[28]M.Turkyilmazoglu,Comp.&Fluids 90(2014)51.

[29]A.Mushtaq,M.Mustafa,T.Hayat,and A.Alsaedi,Comp.&Fluids 27(2016)2223.

[30]A.Mushtaq,M.Mustafa,T.Hayat,and A.Alsaedi,Adv.Powder Technol.27(2017)2223.

[31]A.U.Rehman,R.Mehmood,and S.Nadeem,Appl.Therm.Engr.112(2017)832.

[32]A.Mushtaq,M.Mustafa,T.Hayat,and A.Alsaedi,J.Taiwan Inst.Chem.Engr.45(2014)1176.

[33]O.Pourmehran,M.Rahimi-Gorji,and D.D.Ganji,J.Taiwan Inst.Chem.Engr.65(2016)162.

[34]R.Ahmed and M.Mustafa,J.Mol.Liq.220(2016)635.

[35]T.Javed,M.Sajid,Z.Abbas,and N.Ali,Int.J.Num.Meth.Heat&Fluid Flow 21(2011)903.

[36]R.Tiwari and S.Das,Int.J.Heat Mass Trans.50(2007)2002.

[37]H.C.Brinkman,J.Chem.Phys.20(1952)571.

[38]M.Sheikholeslami,J.Mol.Liq.234(Supplement C):(2017)364.

[39]Mohsen Sheikholeslami,Magnetic Int.J.Hydrogen Energy 42(2017)19611.

[40]M.Sheikholeslami and A.Zeeshan,Comput.Methods Appl.Mech.Eng.320(Supplement C):(2017)68.

[41]R.L.Hamilton and O.K.Crosser,Ind.Engr.Chem.Fund.1(1962)187.

[42]T.Y.Na,Computational Methods in Engineering Boundary Value Problem,Acad.Press,New York(1979)pp.71–76.