Hidden-charm Pentaquark Production at e+e− Colliders∗
Shi-Yuan Li(李世渊) Yan-Rui Liu(刘言锐)Yu-Nan Liu(刘雨男)Zong-Guo Si(司宗国)and Xiao-Feng Zhang(张晓锋)
1School of Physics,Shandong University,Jinan 250100,China
2Institute of Theoretical Physics,Chinese Academy of Science,Beijing 100190,China
To study the properties and production mechanisms of the multiquark state is important to understand the quark model and the strong interactions deeply. The newest evidence for the existance of the pentaquark is from LHCb experiments.Recently,the LHCb Collaboration announced the observation of two charged hidden-charm resonancesproduced in the processThe corresponding decay channelindicates that their minimal quark content isThe most important work at present is to confirm whether the new resonances are pentaquarks or not.Up to now,lots of theoretical investigations have been if nished.Several possibilities for these new resonances to be baryon-meson molecules,two-or three-cluster compact states,etc.,have been discussed.[4−5]In fact,studies on hidden-charm pentaquarks have been started before the observation of thePcstates.In Ref.[6],the interaction between a charmed baryon and an anticharmed meson was studied and it was found that hadronic molecules with the mass above 4 GeV are possible.While in Refs.[7–18],the possibility for this kind of bound state to be the hiddenheavy pentaquark was studied.
In the mean time,the investigations on the pentaquark production in various collisions have also been performed.In Ref.[15],the discovery potential of hidden-charm pentaquarks in the photon-induced production was discussed.In Ref.[19],theJ/ψphotoproduction of the twoPcstates o ffthe proton was proposed to understand their nature.References[20–24]also presented the pentaquark production inγNcollision processes.In Refs.[17,25–27],the hidden-charm pentaquark effects in theπ−preaction were considered.Discussions for the production in bottom baryon decays[28−30]and in heavy-ion orpAcollisions[31−32]can also be found.
However,most of the discussions on production in the present literature are at hadron level and the understanding for the pentaquark structures needs more studies.Obviously,theis not a bound state ofJ/ψand nucleon.A compactpentaquark state with coloredmay be formed through gluon-exchange interactions.The spectrum and qualitative decay properties of the compact pentaquarks[33−34]indicate that such a con figuration is not contradicted with the observedPcstates.In principle,various con figurations of a five-quark system related to different production mechanisms are worthy to be studied in detail.For the hadron-hadron molecules,the produced quarks fragment firstly into various hadrons and then the residual strong interactions between these hadrons lead to possible hadronic molecules.One may study this kind of production mechanism at hadron level.[35]For the compactpentaquark state with coloreda feasible approach is the framework proposed in Ref.[36].Since the gluon is easily converted to a colored charm-anticharm pair,the production rate of the considered compact pentaquark might be signi ficant.We here discuss the production of such a type of pentaquark in the multiproduction process,which can help to better understand their structure as well as the strong interaction mechanism at the hadronization scale.[37]The information of the cross section,rapidity and transverse momentum distributions,etc.,of the relevant particles on a speci fic collider can help the experimentalists to set the proper triggers and cutoffs for the measurements.[35,38]Among the high energy collisions,thee+e−annihilation process is of special advantage for its clean background and one can gain more clear pictures on the color and other structure evolution via the study of the production.
For this kind of hidden-charm pentaquark states,we can rely on the perturbative QCD(PQCD)to calculate the charm quark pair production.On the other hand,how to embed the PQCD result into the production amplitude of the pentaquark,depends on the structure of the state and the framework for the approximation.Here we ignore the consideration of it as hadron bound state,which has been studied in the general case.[35]A benchmark framework could be the heavy quark effective theory,which provides the feasible factorization formulation to connect the PQCD process with the parameterization of the nonperturbative QCD process,i.e.,the PQCD producedc¯ctransiting to the pentaquark,in the rest frame of the bound state.For concrete,we employ the nonrelativistic QCD(NRQCD)factorization framework.The NRQCD factorization approach has been used to discuss the production ofin Ref.[36]and that ofTccin Ref.[39]at variouscolliders.The aim of this paper is to study the hidden-charm pentaquark production via a color-octetpair fragmentation in the process
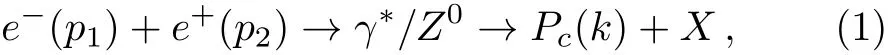
wherep1,p2,andkdenote the momenta of the related particles.The unobserved partXcan always be divided into a perturbative partXPand a nonperturbative partXN,X=XN+XP.The corresponding invariant amplitude can be written as
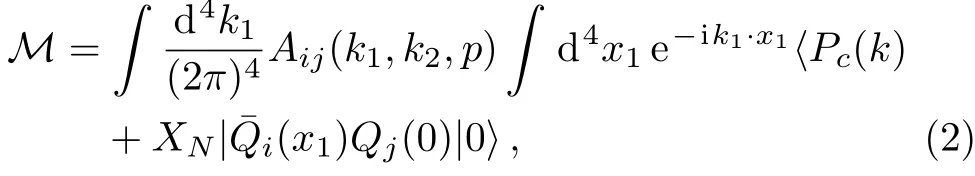
where bothiandjtake Dirac and color indices.Q(x)is the Dirac field for charm quark.k1andk2respectively represent the momentum ofcandin the pentaquark state.pdenotes the total momentum of the partons appearing in the perturbative part.In this paper,we will discuss two cases for the perturbative part,one isand the other isFor the latter case,the quark pair can be light(u,d,s)or heavy(c,b).
First we consider thec¯cgcase.Ifof Eq.(2)is replaced by the state of a free charm-anticharm quark pair with momentak1andk2and a gluon with momentakg,Mis the amplitude for the processso the corresponding contribution is the production of the color-octet charm quark-antiquark pair and then this pair fragments into the pentaquarkPc.
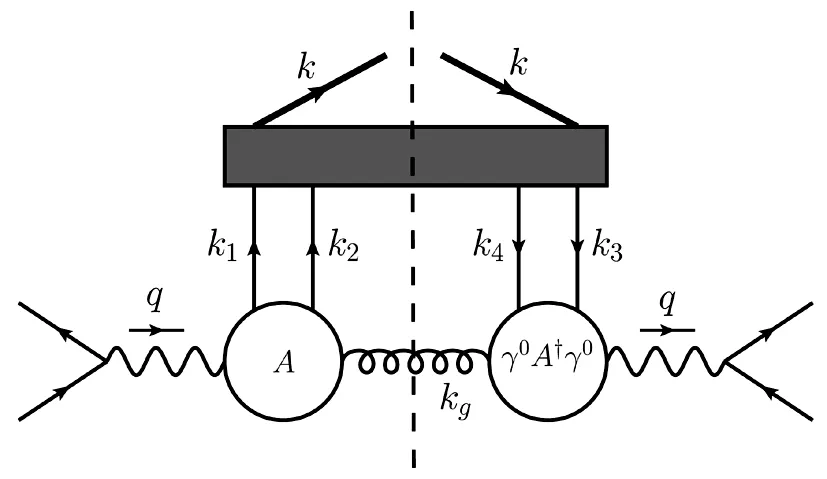
Fig.1 Graphic representation for the contribution in Eq.(5).
For the process
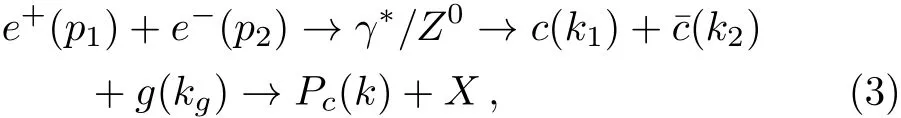
the corresponding cross section can be written as
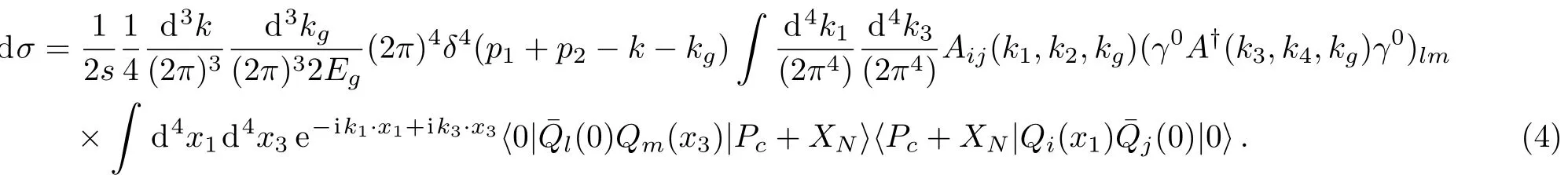
Here we take nonrelativistic normalization forPc.Bothlandmtake Dirac and color indices related toThe spin average of initial leptons,spin summation of finalPc,and the polarization and color summation of gluon are implied.k3andk4respectively represent the momenta ofcand¯cinas shown in Fig.1 where the black box represents the Fourier transformed matrix element of the second line in Eq.(5).By using translational covariance one can eliminate the summation overXN.De fining the creation operatora†(k)forPcwith the three momentumk,we obtain
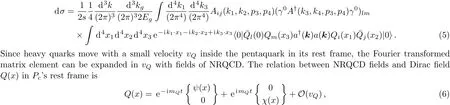
whereψ(x)(χ(x))denotes the Pauli spinor field that annihilates(creates)a heavy(anti-)quark.We will work at the leading order ofvQ.In order to express our results for the Fourier transformed matrix element in a covariant way,we employ the four-velocity of the pentaquark withvµ=kµ/MPc.The Fourier transformed matrix element is related to that in the rest frame:[36]
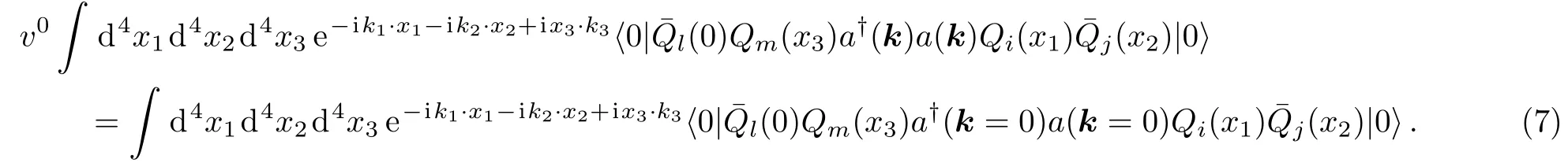
Using Eq.(6),one can expand the matrix element in Eq.(7)withψ†(x)andχ(x).The space-time of the matrix element with NRQCD fields is controlled by the scalemQvQ.Hence at leading order ofvQone can neglect the space-time dependence inψ†(x)andχ(x).With this approximation,the matrix element in Eq.(7)is

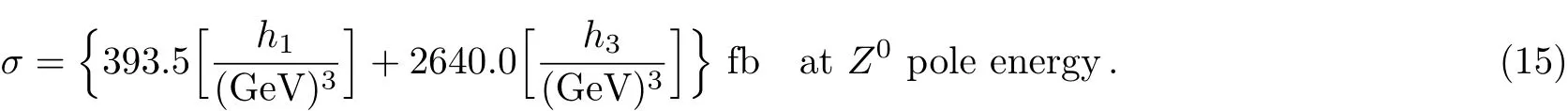
Up to now,h1andh3are still unkown exactly.One can attempt to relate the nonperturbative factorsh1andh3to the wave function of thein the pentaquark,e.g.,
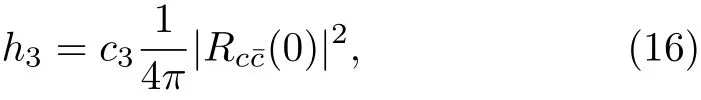
whereRc¯c(ξ)represents the radial wave function of thequark pair in the pentaquarkPcandξis the distance betweencand.In the heavy quark limit,h1andh3are identical up to the corrections of orderi.e.,The coefficientc3is due to the fact thath3is de fined by a color-octet matrix element.In the non-perturbatuive process,the transition from a color-octet state to the final color-singlet pentaquark state introduces extra suppressions of certain power of the relative velocity between the heavy pair in their rest frame,vQ,which we expand the amplitude around its zero value as done above.So the matrix element is suppressed by the small factor proportional to powers ofIn the following numerical calculations we simply takec3as 10−1for the charm sector.
The radial wave functionRc¯c(ξ)can be calculated in potential models.As a first estimation for its value at origin,we consider a simple model where the Hamiltonian contains the kinetic term and the harmonic oscillator as the color con finement potential.[39]With this model,the interaction between the heavy quarks can be easily separated out.This part of Hamiltonian reads
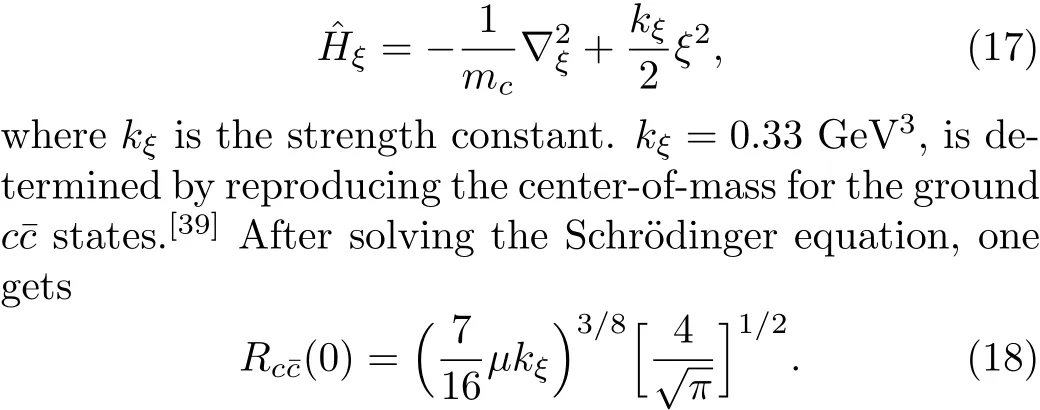
Substituting this expression into Eq.(16),one estimatesh1=h3=0.0036 GeV3,which is used in our numerical calculations.So we obtain thePcproduction cross section of the process(3).The results are listed in Table 1.To investigate the contributions from the spin-singlet and triplet color-octetfragmentation in detail,we study the angular distribution(1/σ)(dσ/d cosθ)of the pentaquarkPc.The results are shown in Fig.2,whereθis the angle between the moving direction of thee−beam and that ofPc.One can see clearly from the figure that the difference between the contribution fromh1and that fromh3is signi ficant.
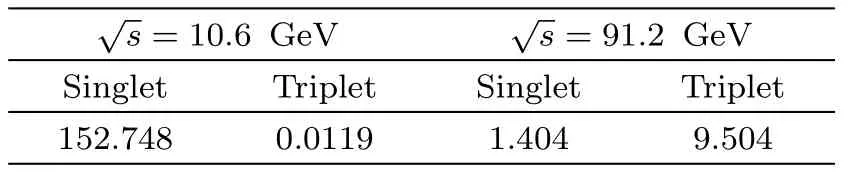
Table 1 Pentaquark proction cross section(in units of fb)of the process(3).
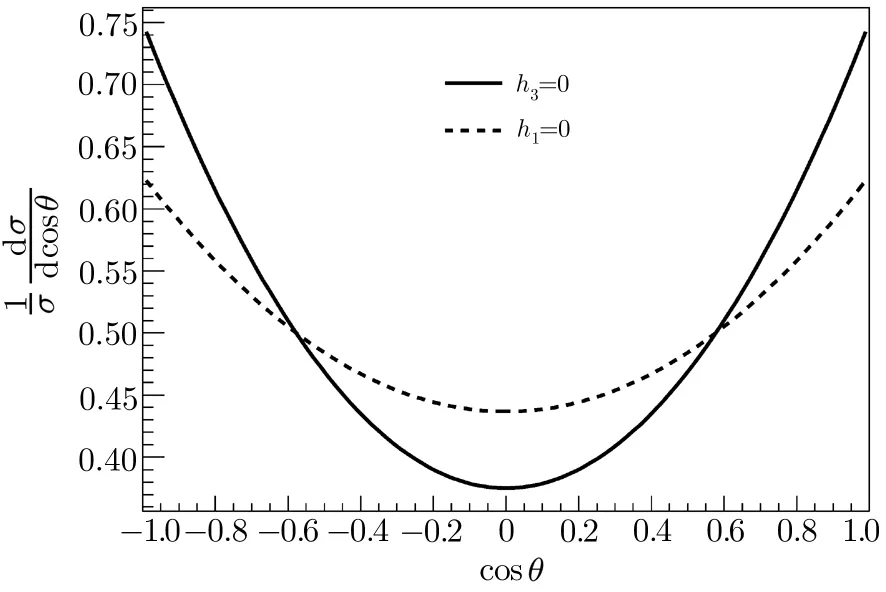
Fig.2 Angular distribution(1/σ)(dσ/d cosθ)of the process(3)at
Next we consider the pentaquark state that can also be produced from the corlor-octetc¯cfragmentation in the process
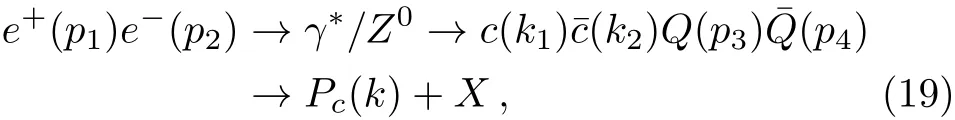
whereQ=c,b,andX=XP+XNas before.p3andp4respectively denote the momentum ofQandetc.For this case,is replaced by the state of four heavy quarks including at least onepair.The corresponding differential cross section can be written as
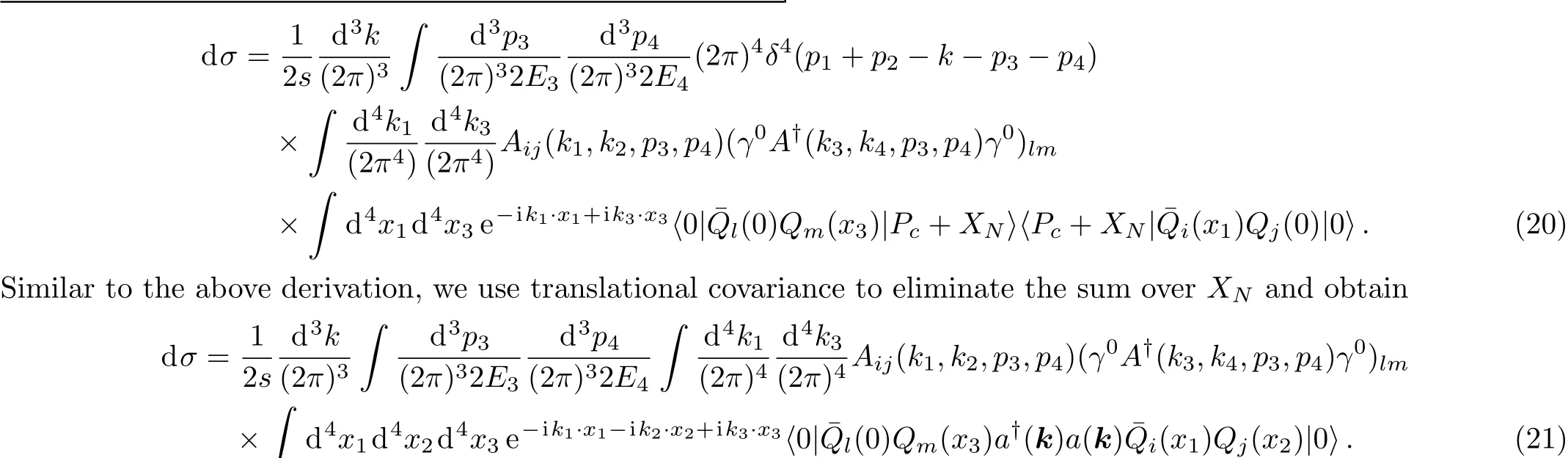
The factorized cross section is displayed in Fig.3.With the help of Eq.(10),the differential cross section for this kind of processes can be further expressed as
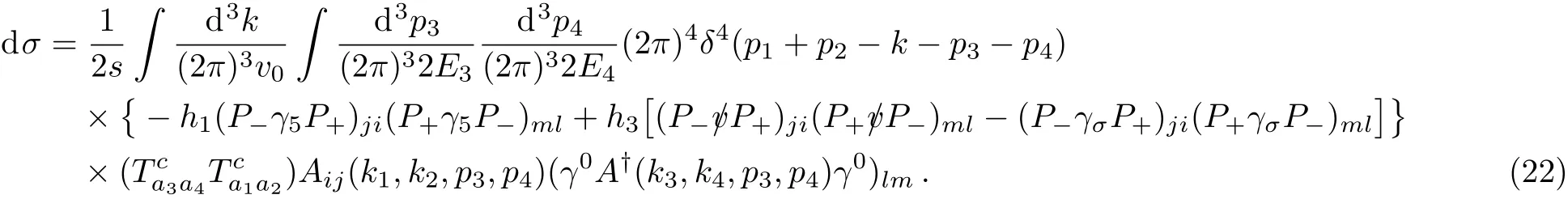
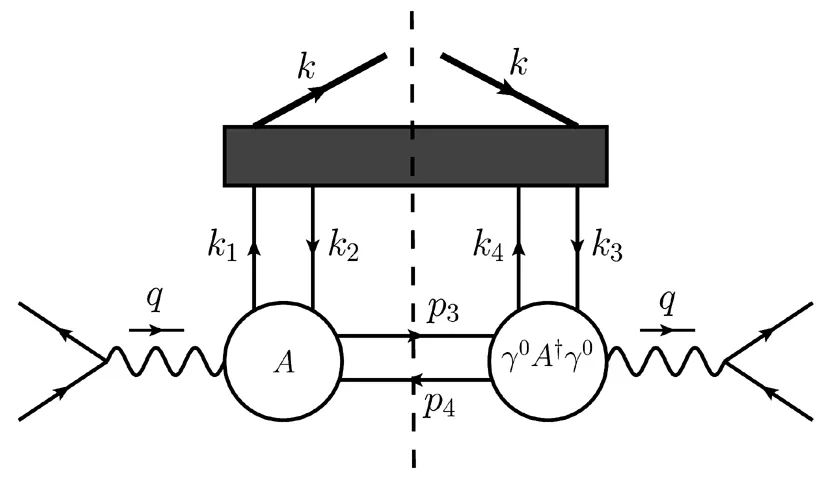
Fig.3 Graphic representation for the contribution in Eq.(21).
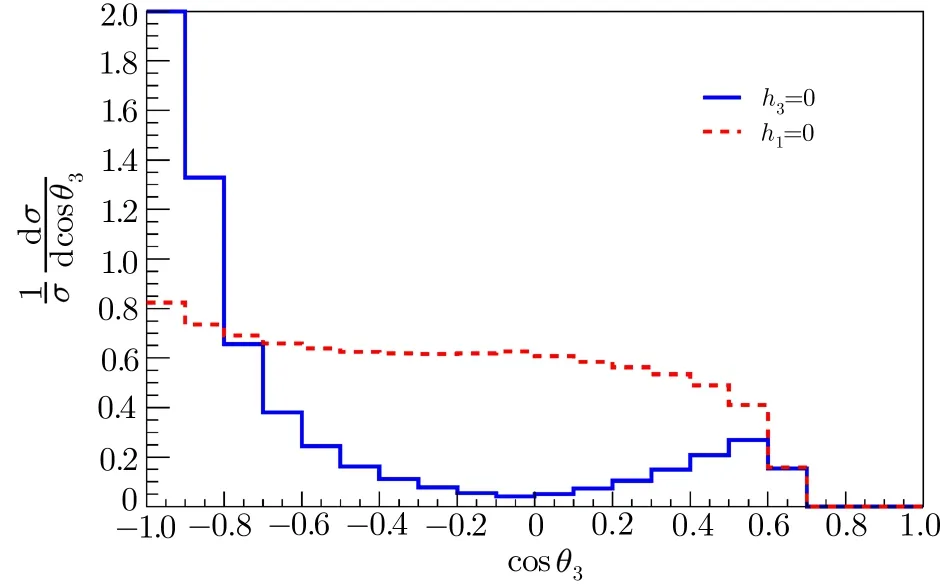
Fig.4 Angular distribution(1/σ)(dσ/d cosθ)of the process(19)at
The angular distribution(1/σ)(dσ/d cosθ)atZ0pole is shown in Fig.4,whereθ3is the angle between the momentum of thecquark(p3)and that ofPc.Because of mass effect,the cross section drops in the small angular range.From Fig.4,our results show that for the case of spinsinglet(h3=0),the cross section is suppressed when the angularθ3is nearπ/2.In this case,one of the free charm quarks takes a relatively large transverse momentum with respect to the c-quark to compensate that of thePc,andPcproduction via gluon fragmentation is prohibited because of the angular momentum conservation at thegq¯qvertex.Employing Eq.(22),we can get the total cross section of pentaquark production related to the process(19)atBfactory energy and atZ0pole.In our following discussions,we simply seth1=h3=0.0036 GeV3.The numerical results of spin-singlet and spin-triplet contributions are given in Table 2.Our results show that atZ0pole energy,thePcproduction cross section contributed from the process(19)is much larger than that from the process(3).

Table 2 Pentaquark production cross section(in units of fb)of the process(19).

Table 3 Pentaquark production cross section(in units of fb)of the process(23).
Finally,we investigate thePcproduction in light quarkq(u,d,s)jet fragmentation by studying the process
The numerical results are presented in Table 3.Since in this process,Pcis produced via the gluon fragmentation,only the spin-triplet component contributes to the cross section.For this process atZ0pole,the cross section contributed from the spin-triplet component is comparable to that of the process(19),which shows that for these two processes,the hidden-charm pentaquark produced from gluon fragmentation is dominant.The cross sections of processes(19)and(23)are both larger than that of the process(3)because of the momentum conservation.The hadron and gluon produced in the final state must recoil from each other in the process(3),which makes the gluon very hard so that it is suppressed.
To summarize,in this paper,we study the compact hidden-charm pentaquark production via the color-octet charm-anticharm pair fragmentation ine+e−annihillation with clean backgrounds.The most straightforward application of our analysis is theBfactory at present and in the future.Based on our above calculations,atBfactory energies,the dominant production process isThis meansPcis dominantly produced in a two-jet like event.Belle collaboration now has collected an integrated luminosity about 1000 fb−1and the events number ofPcproduction could be 105.The future operation ofBfactory will accumulate even more events.So to set a jet algorithm trigger as suggested in Ref.[38]may help us to obtain a clear signal or upper limit forPcproduction ine+e−annihillation.Our method can be easily applied to investigate the production of the pentaquark state including aorc¯bate+e−colliders.In the future,at high energye+e−colliders,e.g.,a high luminosity Z-factory,CEPC and Linear collider,a large number of the events related to our studies in this paper will be accumulated,so that the corresponding measurement with high precision is possible.Once the direct production of the hidden-charm pentaquark states is con firmed ate+e−colliders,it will be very helpful to understand the quark model and the strong interactions.
Acknowledgements
We greatly thank Profs.Yi Jin and Zhong-Juan Yang for helpful discussions.
[1]R.Aaij,et al.,Phys.Rev.Lett.115(2015)072001,[arXiv:1507.03414[hep-ex]].
[2]R.Aaij,et al.,[LHCb Collaboration],Phys.Rev.Lett.117(2016)082002,[arXiv:1604.05708[hep-ex]].
[3]R.Aaij,et al.,[LHCb Collaboration],Phys.Rev.Lett.117(2016)082003,[arXiv:1606.06999[hep-ex]].
[4]H.X.Chen,W.Chen,X.Liu,and S.L.Zhu,Phys.Rep.639(2016)1,[arXiv:1601.02092[hep-ph]].
[5]R.Chen,X.Liu,and S.L.Zhu,Nucl.Phys.A 954(2016)406,[arXiv:1601.03233[hep-ph]].
[6]J.J.Wu,R.Molina,E.Oset,and B.S.Zou,Phys.Rev.Lett.105(2010)232001,[arXiv:1007.0573[nucl-th]].
[7]J.J.Wu,R.Molina,E.Oset,and B.S.Zou,Phys.Rev.C 84(2011)015202,[arXiv:1011.2399[nucl-th]].
[8]Z.C.Yang,Z.F.Sun,J.He,et al.,Chin.Phys.C 36(2012)6,[arXiv:1105.2901[hep-ph]].
[9]W.L.Wang,F.Huang,Z.Y.Zhang,and B.S.Zou,Phys.Rev.C 84(2011)015203,[arXiv:1101.0453[nucl-th]].
[10]S.G.Yuan,K.W.Wei,J.He,et al.,Eur.Phys.J.A 48(2012)61,[arXiv:1201.0807[nucl-th]].
[11]J.J.Wu,T.S.H.Lee,and B.S.Zou,Phys.Rev.C 85(2012)044002,[arXiv:1202.1036[nucl-th]].
[12]C.Garcia-Recio,J.Nieves,O.Romanets,et al.,Phys.Rev.D 87(2013)074034,[arXiv:1302.6938[hep-ph]].
[13]C.W.Xiao,J.Nieves,and E.Oset,Phys.Rev.D 88(2013)056012,[arXiv:1304.5368[hep-ph]].
[14]T.Uchino,W.H.Liang,and E.Oset,Eur.Phys.J.A 52(2016)43,[arXiv:1504.05726[hep-ph]].
[15]Y.Huang,J.He,H.F.Zhang,and X.R.Chen,J.Phys.G 41(2014)115004,[arXiv:1305.4434[nucl-th]].
[16]X.Y.Wang and X.R.Chen,Eur.Phys.J.A 51(2015)85,[arXiv:1504.01075[hep-ph]].
[17]E.J.Garzon and J.J.Xie,Phys.Rev.C 92(2015)035201,[arXiv:1506.06834[hep-ph]].
[18]X.Q.Li and X.Liu,Eur.Phys.J.C 74(2014)3198,[arXiv:1409.3332[hep-ph]].
[19]Q.Wang,X.H.Liu,and Q.Zhao,Phys.Rev.D 92(2015)034022,[arXiv:1508.00339[hep-ph]].
[20]V.Kubarovsky and M.B.Voloshin,Phys.Rev.D 92(2015)031502,[arXiv:1508.00888[hep-ph]].
[21]M.Karliner and J.L.Rosner,Phys.Lett.B 752(2016)329,[arXiv:1508.01496[hep-ph]].
[22]Y.Huang,J.J.Xie,J.He,et al.,Chin.Phys.C 40(2016)124104,[arXiv:1604.05969[nucl-th]].
[23]A.N.H.Blin,C.Fernndez-Ramrez,A.Jackura,et al.,Phys.Rev.D 94(2016)034002,[arXiv:1606.08912[hepph]].
[24]V.Kubarovsky and M.B.Voloshin,arXiv:1609.00050[hep-ph].
[25]Q.F.L,X.Y.Wang,J.J.Xie,et al.,Phys.Rev.D 93(2016)034009,[arXiv:1510.06271[hep-ph]].
[26]S.H.Kim,H.C.Kim,and A.Hosaka,Phys.Lett.B 763(2016)358,[arXiv:1605.02919[hep-ph]].
[27]Z.Ouyang and L.P.Zou,arXiv:1512.02130[hep-ph].
[28]H.Y.Cheng and C.K.Chua,Phys.Rev.D 92(2015)096009,[arXiv:1509.03708[hep-ph]].
[29]Y.K.Hsiao and C.Q.Geng Phys.Lett.B 751(2015)572,[arXiv:1508.03910[hep-ph]].
[30]A.Ali,I.Ahmed,M.J.Aslam,and A.Rehman,Phys.Rev.D 94(2016)054001,[arXiv:1607.00987[hep-ph]].
[31]R.Q.Wang,J.Song,K.J.Sun,et al.,Phys.Rev.C 94(2016)044913,[arXiv:1601.02835[hep-ph]].
[32]I.Schmidt and M.Siddikov,Phys.Rev.D 93(2016)094005,[arXiv:1601.05621[hep-ph]].
[33]J.Wu,Y.R.Liu,K.Chen,et al.,Phys.Rev.D 95(2017)034002,[arXiv:1701.03873[hep-ph]].
[34]S.Takeuchi and M.Takizawa,Phys.Lett.B 764(2017)254,[arXiv:1608.05475[hep-ph]].
[35]Y.Jin,S.Y.Li,Y.R.Liu,et al.,Chin.Phys.C 41(2017)083106,[arXiv:1610.04411[hep-ph]].
[36]J.P.Ma and Z.G.Si,Phys.Lett.B 568(2003)135,[hep-ph/0305079].
[37]Y.Jin,S.Y.Li,and S.Q.Li,Phys.Rev.D 94(2016)014023,[arXiv:1603.03250[hep-ph]].
[38]Y.Jin,S.Y.Li,Y.R.Liu,et al.,Phys.Rev.D 89(2014)094006,[arXiv:1401.6652[hep-ph]].
[39]T.Hyodo,Y.R.Liu,M.Oka,et al.,Phys.Lett.B 721(2013)56.
[40]G.T.Bodwin,E.Braaten,and G.P.Lepage,Phys.Rev.D 51(1995)1125,Erratum:[Phys.Rev.D 55(1997)5853],[hep-ph/9407339].
 Communications in Theoretical Physics2018年3期
Communications in Theoretical Physics2018年3期
- Communications in Theoretical Physics的其它文章
- A First-Principles Study on the Vibrational and Electronic Properties of Zr-C MXenes∗
- Cole-Hopf Transformation Based Lattice Boltzmann Model for One-dimensional Burgers’Equation∗
- Thermally Radiative Rotating Magneto-Nano fl uid Flow over an Exponential Sheet with Heat Generation and Viscous Dissipation:A Comparative Study
- Decoherence Effect and Beam Splitters for Production of Quasi-Ampli fied Entangled Quantum Optical Light
- Application of Connection in Molecular Dynamics
- Wilsonian Renormalization Group and the Lippmann-Schwinger Equation with a Multitude of Cuto ffParameters∗
