Decoherence Effect and Beam Splitters for Production of Quasi-Ampli fied Entangled Quantum Optical Light
Saad R fi fi
Laboratoire des Sciences et Technologies Avanc´ees,Facult´e Polydisciplinaire de Larache,Universit´e Abdelmalek ESSAADI,Route de Rabat,Km 2–Larache BP.745–Larache 92004,Maroc
1 Introduction
Optical coherent states are classical light fields with high purity,and are essential tools of information in optical areas. If these states,especially the entangled ones,[1−2]could be controlled in the quantum limit,then novel quantum-enhanced functions such as coherent-state quantum computing(CSQC),[3−4]quantum metrology,[5]and a quantum repeater[6−7]could be realized in the networks.Then,entangled coherent states have a large important applications that are investigated in several physical systems.[8−11]
Consider the case where some of quantum information(or classical parameter value)is encoded in the complex amplitudeαof a coherent stateIf the state amplitude is made too small(generally by losses),then the strong overlap between different states can make it impossible to correctly distinguish among them.To make them exactly distinguishable for quantum information applications,including precision measurements,[12]quantum computation,[13]quantum teleportation[14]and quantum key distribution,[15]we need to amplify them with a good way on the limit of our need.
In this context,many works are focused on the ampli fication methods of coherent states with higher fidelity.For example,Ref.[16]has implemented a quantum setup containing interferometers,single-photon detectors and linear polarized fibers to achieve the ampli fication task.Reference[17]has realized the ampli fication of superposition of coherent states by using Beam splitters.References[18–19]have also realized this ampli fication using successive photon additions and photon subtractions(photon creation and annihilation operators).In addition,Ref.[20]has achieved a hybrid linear ampli fier in order to establish a probabilistic cloning.In the same context,other works achieved a non-Gaussian encoding operations[21−23]to implement Error correction in the purpose of ampli fication.
Although,the above ampli fication protocols avoid working on the noisy limit due to the amplitude attenuation made by the noise effect.In other words,the noise gives rise to a phase uncertainty that plays an increasingly devastating role for the estimation of the phase as the excitation of the coherent states decreases.So,the state must be ampli fied in such a way that its phase variance is reduced as compared to the input state.Indeed,improving coherent states entanglement by its ampli fications[24]is an interesting research field.
In the current work,we exploit positively the decoherence effect,to realize an entangled coherent states as quantum channels starting from separate ones,that is by using a symmetric decoherent noisy environment.[25−27]Indeed,the used decoherence model is based on the interaction of the signal with a beam splitters in a vacuum mode and a chosen transmittance parameterη.This corresponds to a Gaussian Error[28−29]implementation that will be helpful in our scheme to generate an attenuated quantum channels based on optical light.
After that,for the robustness of continuous variables quantum key distribution protocols,especially in the presence of an eavesdropper attacks using such quantum channels.We eliminate the photon losses and the amplitude damping caused generally by the noise effect as mentioned before.Then,we establish a quasi-ampli fication process of the realized entanglement,in a way that we can control the ampli fication rate.Otherwise,we discuss the attenuation process of the coherent states amplitude.To highlight the strength of our scheme,we study and analyze the behavior increase of the amplitude rate,the entanglement amount of the output entangled system after application of the proposed scheme.We analyze also the fidelity of the quasi-ampli fication process.Our protocol is useful in the production of either the quasi-ampli fied entangled coherent states or the attenuated entangled coherent states according to our need.We add that the protocol application is easier in the current technology because it needs only a simple light source as a diode laser and beam splitters(for decoherence effect and quasi-ampli fication process),knowing that the measurement will be efficient thanks to the homodyne detection of coherent light.
2 Production Model of Entangled Coherent States via Noise Effect
The decoherence effect model used in our work is realized by using the following process:
A Beam Splitter in the vacuum mode with a chosen transmittance parameterηin interaction with a coherent statecauses a photon losses and an amplitude damping as follows:
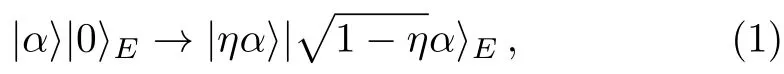
whereis the vacuum mode corresponding to the channel andηis the transmittance parameter(which is equal to the channel noise rate;the fraction of photons that survive the noise).
We mention that the explanation of the overall steps of the used model is described initially in Fig.1.
Consider a qubit state initially inhabits in a coherent lightb:
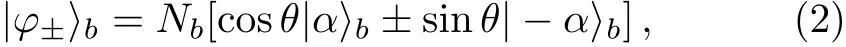
knowing thatNbis the normalized factor of the state(2),θis unknown to us andConsidering also another qubit state initially inhabits in a coherent lighta:
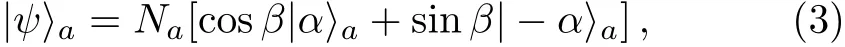
whereNais the normalized factor of the state(3),βis unknown to us and 0
Secondly,we consider the fact that the two modes of the statessuffer both from the photon losses after crossing together two symmetric beam splitters of the vacuum mode as de fined above in the decoherence model.
Then,we get:
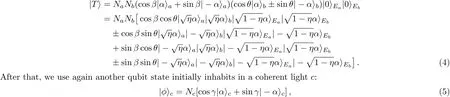
knowing thatNcis the normalized factor of the state(5),γis unknown to us and 0<γ≤π/2.
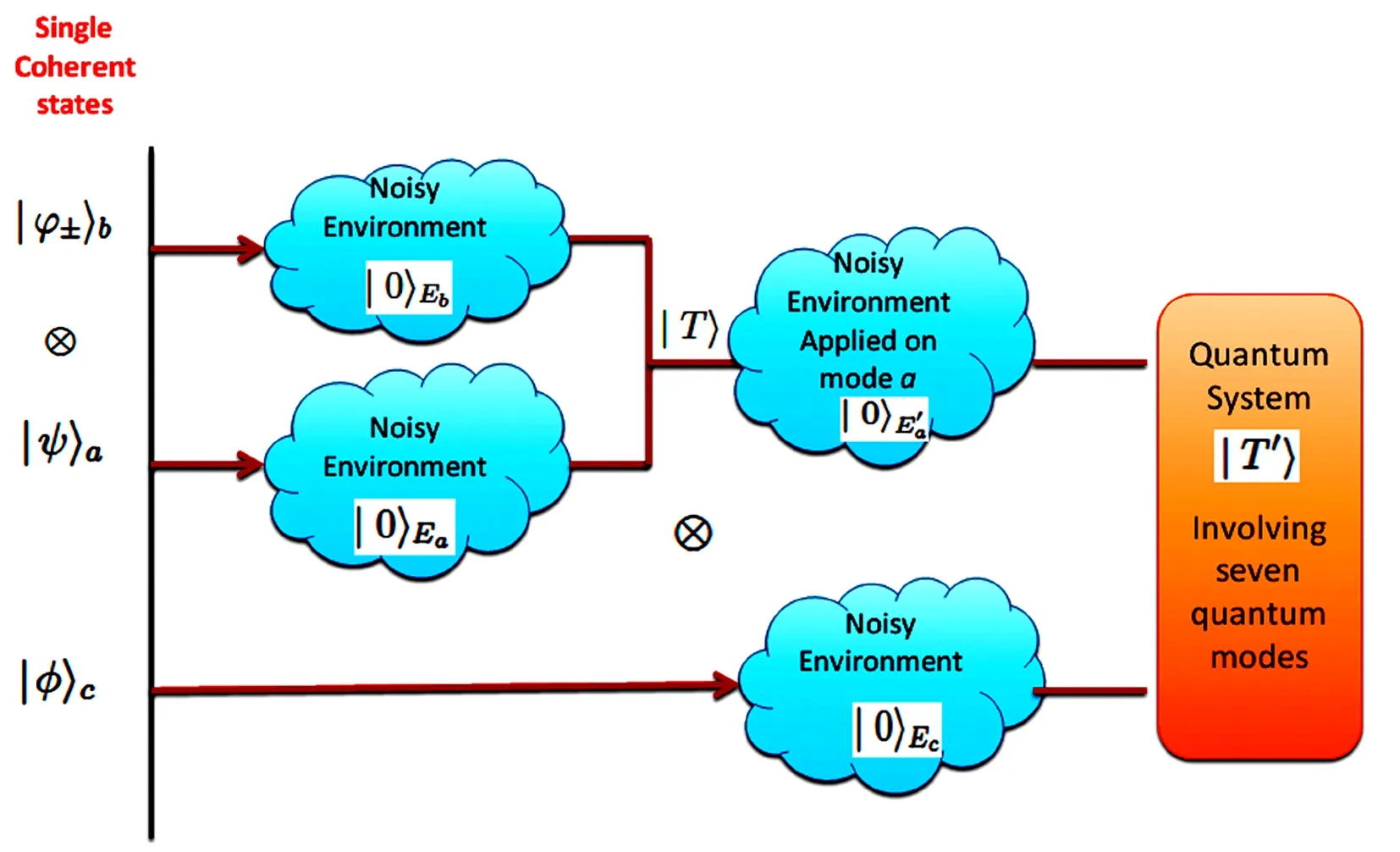
Fig.1 (Color online)The scheme that describes the applied steps on single coherent states a,b,and c to reach Eq.(8)before the final phase of local measurements for entanglement production;to get an attenuated quantum channels based on optical light.
If the two modesaandcof the whole systemsuffer both too from the photon losses after crossing together the symmetric noisy environment(Fig.1).Then,we get:


Table 1 Different possibilities of produced attenuated quantum channels via decoherence effect after obtaining measurement outcomes on subsystems b and Eb.
Obviously,we have exploited our model of decoherence effect by beam splitters noise to produce four types of quantum channels.It includes an entanglement that has attenuated amplitudes,which is normal due to the noisy production tool.However,to improve these produced entangled states,we discuss in the next section a proposed model to enhance its quality by applying quasi-ampli fication.
3 Quasi-Ampli fication Model of such Quantum Channels
In this section,we propose to increase the amplitude rate of the produced entangled coherent states that we have generated before.Also,an entanglement improvement is done for the same produced entangled state.For this purpose,we use a 50:50 beam splitter(the re fl ected beam which suffers aπ/2 phase shift).After that,the fidelity of the quasi-ampli fication process is measured to highlight the strength of the protocol.
3.1 Improvement of Ampli fication Rate
Consider the first case of Table 1,when we get the following entangled coherent state:
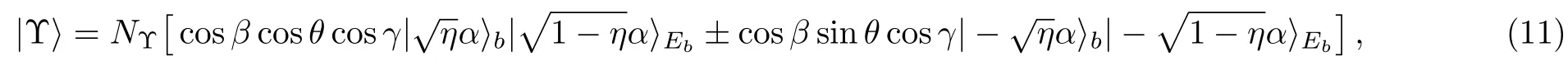
whereNΥis the normalized factor of the recovered state(11).
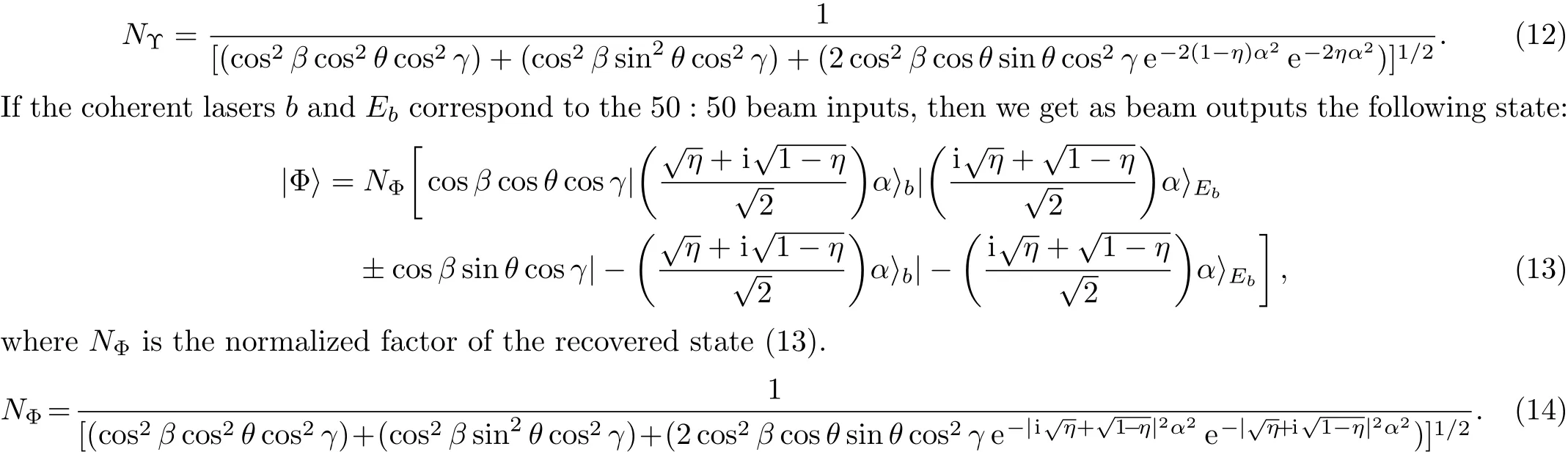
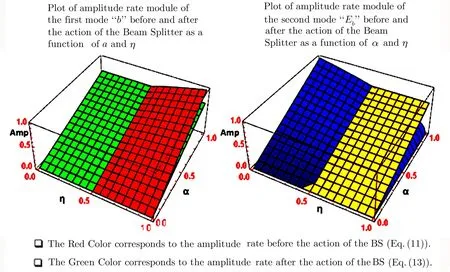
Fig.2 (Color online)Comparative study of the action effect of the Beam Splitter on each mode of the entangled state(11).
We show in Fig.2 that,comparing with the amplitude rate of the modebin Eq.(11),an increasing amplitude rate behavior appears in the modeb,which belongs to the output coherent laser of Eq.(13).
This ampli fication behavior appears especially when the noise rate(the transmission parameter of the used beam splitter in the decoherence model)is 0<η<1/2,whatever theα>0 value.
However,another ampli fication side is obtained otherwise in the modeEbof Eq.(13)when the noise rate of the used decoherence model is 1/2<η<1 during the production of the entangled coherent states.
We mention that with the same process,using the beam splitter as an optical device,we can amplify the other obtained attenuated entangled coherent states in Table 1,as we have proceeded taking the first case as mean example.
3.2 Improvement of Entanglement
Now,to analyze the effect of our quasi-ampli fication scheme on entanglement,we measure the amount of entanglement of the input and the output entangled systems(Eqs.(11)and(13)),by using concurrence.
For this reason,to have orthogonal basis,we apply the following transformations:
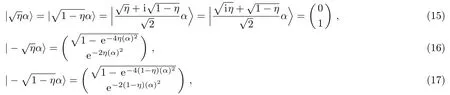
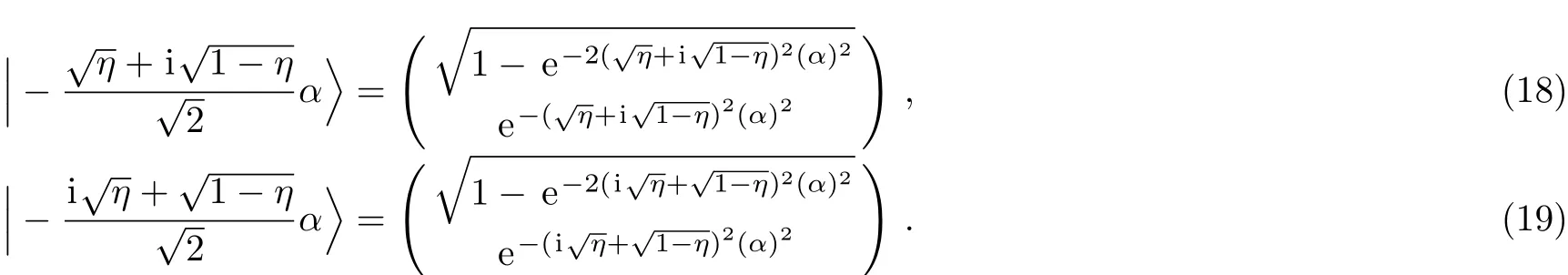
Then,after calculating concurrence[30−32]as an entanglement parameter,we find that for the states(11)and(13),the concurrence depends only on the values ofη,α,andθ.
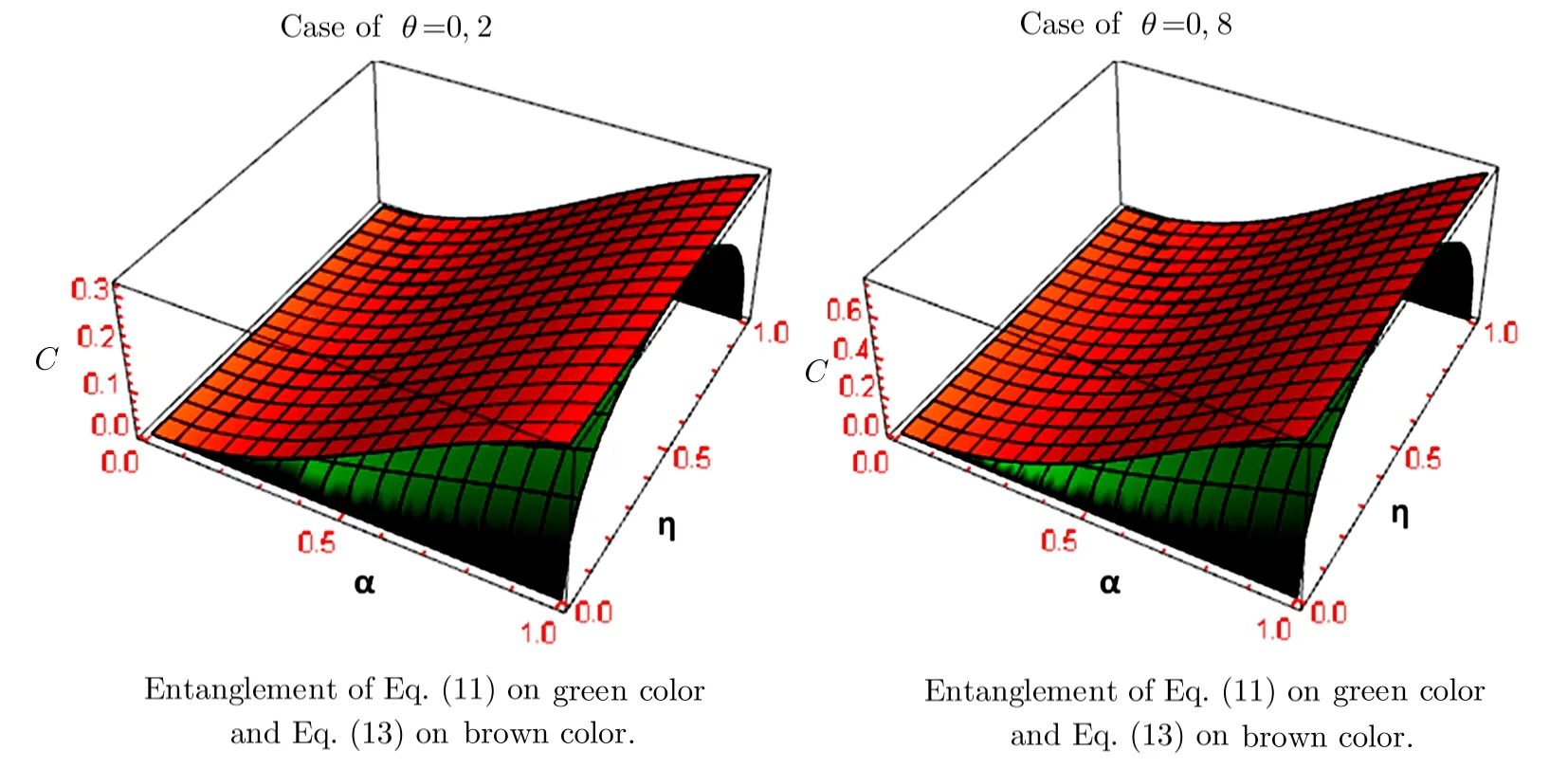
Fig.3 (Color online)Comparative study between entanglement of the state in Eq.(11)and the state in Eq.(13)for two different values of θ.
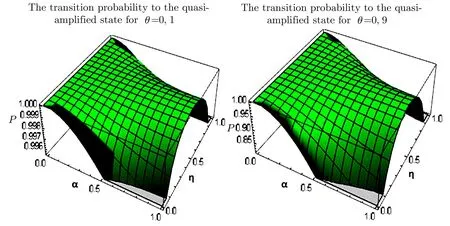
Fig.4 (Color online)The probability of transition from the input state in Eq.(11)to the output state in Eq.(13)for two different values of θ.
After that,we plot in Fig.3 the behavior of entanglement for both states as function ofηandαfor two different values ofθ.Then,it appears clearly from the plot that the entanglement of the state in Eq.(13)after the process of quasi-ampli fication becomes better compared with the entanglement of state in Eq.(11).Also,the entanglement amount increases with the increasing value ofθ.We note that Fig.3 shows that for the output state in Eq.(13),whatever the values ofηthe state keeps its higher entanglement amount,which is not the case for the input state in the extreme values ofη.
3.3 Scheme Probability of Transition to the Quasi-Ampli fied State
To quantify the probability of transition from the input state in Eq.(11)to the output state in Eq.(13).We calculate the probability,which gives the gap between the two states after applying the quasi-ampli fication scheme using the beam splitter.For this reason,we apply the transformations in Eqs.(16)–(19)to the orthogonal basis for both states.After that,we measure the probability.In this context,we find that the probability expression does not depend on the parametersβandγ,but it depends only onα,η,andθ.Indeed,we get for this probability,the corresponding behavior in Fig.4.It seems clearly from Fig.4 that the probability of transition to the quasi-ampli fied state reaches maximum values when we use low values ofθ.
4 Discussion and Conclusion
Signal of separate single coherent states are interacted with a beam splitters in the vacuum mode of chosen transmission parameterη.This proposed model causes an amplitude damping and photon losses.However,we exploit positively the decoherence effect of the model to produce an attenuated quantum channels.After that,to eliminate the amplitude attenuation that are caused by the noise effect,in such a way that its phase variance will be reduced,we propose an improvement model of the entanglement such as the amplitude rate.
Indeed,after using a beam splitter applied on the two modes of the entangled coherent state,we have succeeded to increase the entanglement amount of the produced entangled state as it is shown in Fig.3.Also,according to the noise rate valueηand our need as it is shown in Fig.2,we have succeeded to increase the amplitude rate of one chosen optical light mode among the two modes.Then,we can control the noise rate value to amplify a single mode that we have chosen according to our need and our applications.It seems obviously that our model ampli fies just one mode of the produced entangled coherent states instead of two modes ampli fication.This fact is the strong point of our model especially in the Quantum Key Distribution applications(QKD).In other words,to avoid the threats of untrusted channels,which come from the attenuation,we can complicate the eavesdropping attacks during the continuous variables QKD,by controlling the legitimate channel modes to decrease the degradation of the key rate.In this context,we can imagine that the eavesdropper will not have any idea about which mode of the channel is ampli fied by the trusted users(the sender and the receiver),because only them who control the target mode in the process of ampli fication.So,the probability of attacks success by the untrusted user will be reduced.
We notice that the quasi-ampli fication phase enhance the amplitude rate of our chosen mode in the entangled coherent light such as the entanglement amount.However,the best achieved increase of the entanglement amount is done when we use higher values of the parameterθ.Although,the probability of transition from the produced attenuated entangled state to the quasi-ampli fied state takes a good values when we use a low values ofθ.Consequently,our scheme increases the amplitude rate,the entanglement amount with higher fidelity,but for reaching the maximum efficiency and higher improvement it is clearly recommended to use an intermediate values ofθ.
[1]S.R fi fiand M.El Baz,Appl.Math.Inf.Sci.9(2015)1199.
[2]S.R fi fiand M.El Baz,Int.J.Theor.Phys.(2015),DOI 10.1007/s10773-015-2556-8.
[3]T.C.Ralph,A.Gilchrist,G.Milburn,et al.,Phys.Rev.A 68(2003)042319.
[4]A.P.Lund,T.C.Ralph,and H.L.Haselgrove,Phys.Rev.Lett.100(2008)030503.
[5]J.Joo,W.J.Munro,and T.Spiller,Phys.Rev.Lett.107(2011)083601.
[6]N.Sangouard,et al.,J.Opt.Soc.Am.B 27(2010)A137.
[7]J.B.Brask,et al.,Phys.Rev.Lett.105(2010)160501.
[10]S. R fi fi, Int. J. Theor. Phys. 55 (2016) 4553,DOI:10.1007/s10773-016-3078-8.
[12]Y.M.Zhang,et al.,Phys.Rev.A 88(2013)043832.
[13]J.Kim,et al.,Opt.Commun.337(2015)7982.
[14]S.R fi fiand M.El Baz,Quantum Inf.Process.14(2015)6781,DOI:10.1007/s11128-014-0827-6.
[15]D.S.Simon,G.Jaeger,and A.V.Sergienko,Phys.Rev.A 89(2014)012315.
[16]J.D.Ross,et al.,Phys.Rev.Lett.114(2015)120505.
[21]T.C.Ralph,Phys.Rev.A 84(2011)022339.
[22]R.Wickert,N.K.Bernardes,and P.van Loock,Phys.Rev.A 81(2010)062344.
[23]S.Glancy,H.M.Vasconcelos,and T.C.Ralph,Phys.Rev.A 70(2004)022317.
[25]R.Wickert and P.van Loock,Phys.Rev.A 89(2014)052309.
[26]I.Derkach,C.Vladyslav Usenko,and R.Filip,Phys.Rev.A 93(2016)032309.
[27]Y.Yao,et al.,Phys.Lett.A 375(2011)3762.
[28]M.Lassen,et al.,Phys.Rev.Lett.111(2013)180502.
[30]S.R fi fi,F.Siyouri,M.El Baz,and Y.Hassouni,J.Korean Phys.Society 9(2015)1199.
[31]F.Siyouri,S.R fi fi,M.El Baz,and Y.Hassouni,Commun.Theor.Phys.65(2016)447.
[32]S.R fi fiand F.Siyouri,Found.Phys.46(2016)1461,DOI:10.1007/s10701-016-0024-9.
 Communications in Theoretical Physics2018年3期
Communications in Theoretical Physics2018年3期
- Communications in Theoretical Physics的其它文章
- A First-Principles Study on the Vibrational and Electronic Properties of Zr-C MXenes∗
- Cole-Hopf Transformation Based Lattice Boltzmann Model for One-dimensional Burgers’Equation∗
- Thermally Radiative Rotating Magneto-Nano fl uid Flow over an Exponential Sheet with Heat Generation and Viscous Dissipation:A Comparative Study
- Application of Connection in Molecular Dynamics
- Wilsonian Renormalization Group and the Lippmann-Schwinger Equation with a Multitude of Cuto ffParameters∗
- Higgs and Bottom Quarks Associated Production at High Energy Colliders in the Littlest Higgs Model with T-Parity∗
