Application of Connection in Molecular Dynamics

Xin Sun(孙鑫)

Department of Physics and State Key Laboratory of Surface Physics,Fudan University,Shanghai 200433,China

Collaborative Innovation Center of Advanced Microstructure,Nanjing 210093,China

1 Introduction

In molecule,since nuclei are much heavier than electrons,they are considered as classical particle,this is semi-quantum molecular dynamics.The electronic states in molecule are time-dependent superpositions of all the eigenstates,and the electron distribution is changing with the time,this is dynamical evolution.At the same time,the nuclear motion makes the base vectors of the eigenstates continuously varying,and it indirectly induces additional evolution,it is kinematical evolution.

Recent years,the semi-quantum molecular dynamics,especially the Ehrenfest dynamics,have got further progress,[1−4]where the dynamical evolution can be expressed analytically,and its calculation is transparent.However,the kinematical one depends on complicated numerical calculation,[5−7]which causes some confusions.It is needed to establish an analytic formula to express the kinematical evolution,then all the results become de finite.This paper will provide one approach based on the connection in the geometry to derive such an expression.

A molecule consists ofNnuclei andMelectrons,the coordinates of nuclei areand that of electrons are.Rdetermines the con figuration and shape of the molecule.

The electronic Hamiltonian is Hilbert space.

2 Formulation

The time-dependent Schrödinger equation is

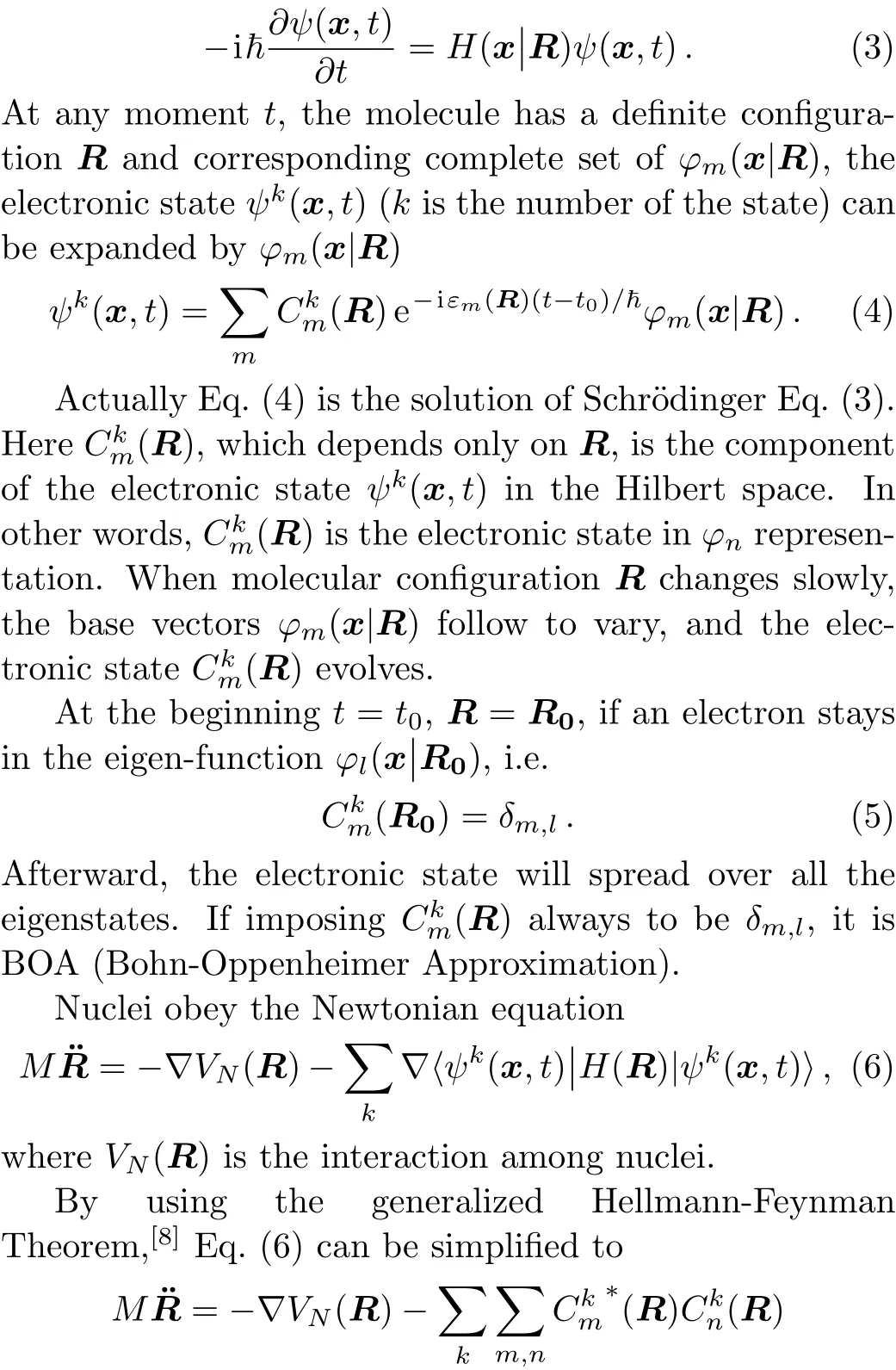
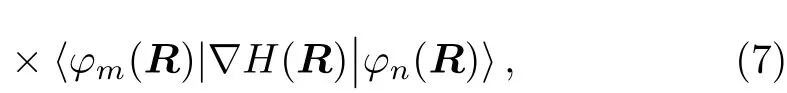
By solving the combined equations of Schrödinger Eq.(3)and Newtonian Eq.(7),both the electronic statesand nuclear motioncan be obtained.Since nuclear motion is much slower than that of electrons,a practical method to solve these combined equations is the iteration approach step by step,each step takes a short time interval ∆t. In solving the Schrödinger Eq.(3),withincan be fixed and Eq.(3)becomes equation,it is the dynamical evolution caused by the phase change. The second partcomes from the transformation of base vectorit is the kinematic evolution.

The rest problem is how to calculate the matrixA primary method is numerical calculation,and such method needs a lot of computer work.As usual,heavy numerical calculation may cause uncertainty,one is energy shift. If we can derive an analytic expression for the kinematic evolutionit is desirable.This goal can be achieved by using the connection of fiber bundle.The details are presented in the following.

3 Connection of Fiber Bundle

The change from con figurationis a deformation operatorwhich includes unit elementinverse elementD−1(i,j)=D(j,i),multiplicationassociativity of productsHere,the multiplication has a restriction:two operators can multiply only they are connected.With such multiplication,the deformation operators form a special group,and the deformation groupD(i,j)can be represented in terms of matrix,based on the Hamiltonian(1).

In base spaceR,at any point,a linear Hilbert space with the base vectorscan be attached,it is a fiber bundle.

During the deformation fromthe bases are transformed fromSinceare complete set,can be expanded in terms of

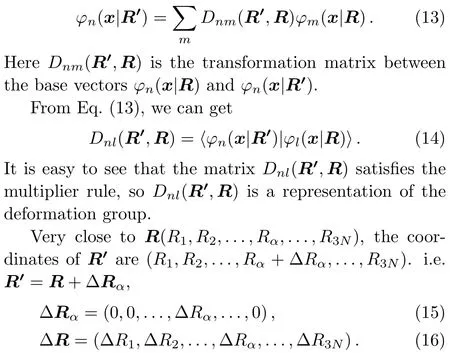
The change rate of the transformation matrixin the componentRαis

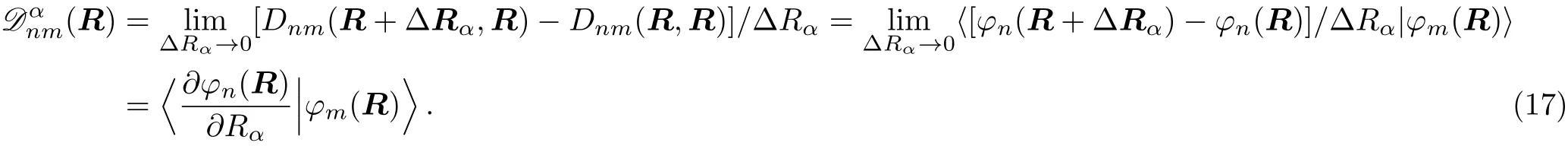
In geometry,this ratedemonstrates the orientation correlation between neighboring base vectors of fiber bundles.Here,in the molecule,it is the connection of deformation.In base spaceR,is a vector with the component indexα.In the Hilbert space of fiber bundle,is a tensor with the indexes(n,m).

By the way,in algebra,is the in finitesimal generator of the representation

By using the perturbation theory,we can get

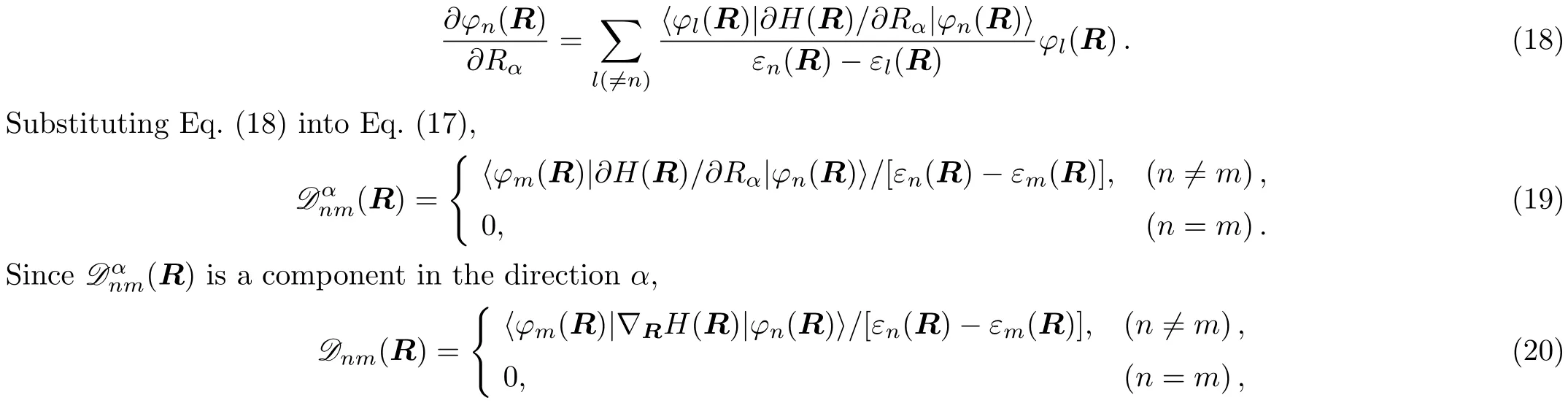
is the vector itself with 3Ncomponents(α=1,2,...,3N).is the connection of molecule deformation.It is notable that the main part of the connectionis the gradient matrixwhich has been got in Newtonian Eq.(7).

By usingfrom Eq.(17),we can get

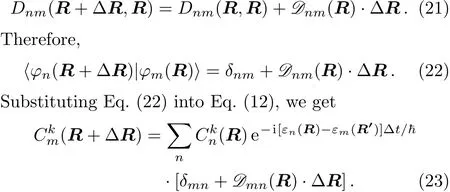
In Eq.(23),the last termis the kinematic evolution,which has been analytically expressed by the connection(Eq.(20))of the fiber bundle,and original heavy numerical calculation is avoided.If neglecting the connection the electronic state would not be able to spread over different eigenfunctions,that is the BOA.

Finally,by solving combined equations(7)and(23),the evolutions of electronic stateand the nuclear con figurationR(t)can be determined.

Polymers are chain-like molecules.Since they are onedimensional systems,the polymers have prominent selftrapping,which is a typical deformation effect.The selftrapping produces many novel phenomena in polymers,such as photoinduced spin- fl ipping of charge carries and charge- fl ipping of spin carries.The Ehrenfest dynamics has been used to study these processes.[6−7]But these works have a problem,that their numerical calculations are very heavy,even getting some uncertainty.The connection of fibre bundle can be used to reduce the numerical calculation and make results transparent.

4 Conclusion

Molecule is a physical model of the fiber bundle,which can be used to build analytic expression for molecular dynamics and simplify numerical calculation.

Acknowledgements

The author would like to thank Professor R.B.Tao,Professor Y.S.Wu,Mr.Y.S.Zhang and Mr.D.Y.Jiang for their helpful discussions.

[1]S.Stafström,Chem.Soc.Rev.39(2010)2484.

[2]A.P.Hors field,et al.,J.Phys.Condens.Matter.16(2004)3609.

[3]A.Johansson and S.Stafström,Phys.Rev.Lett.86(2001)3602.

[4]Z.An,C.Q.Wu,and X.Sun,Phys.Rev.Lett.93(2004)216407.

[5]Z.Sun and S.Stafström,J.Chem.Phys.135(2011)074902.

[6]J.Dong,W.Si,and C.Q.Wu,J.Chem.Phys.144(2016)144905.

[7]B.Di,S.Yang,Y.Zhang,et al.,J.Phys.Chem.C 117(2013)18675.

[8]X.Sun,Chin.Phys.Lett.33(2016)123601.