离轴径向偏振高斯光束的非傍轴传输特性
倪 波, 郭利娜, 吴泳波, 唐志列*
(1.华南师范大学物理与电信工程学院, 广州 510006; 2.广东技术师范学院电子与信息学院, 广州 510665)
离轴径向偏振高斯光束的非傍轴传输特性
倪波1, 郭利娜2, 吴泳波1, 唐志列1*
(1.华南师范大学物理与电信工程学院, 广州 510006; 2.广东技术师范学院电子与信息学院, 广州 510665)
基于矢量瑞利-索末菲衍射积分,研究了离轴径向偏振高斯光束的非傍轴传输特性,推导了离轴径向偏振高斯光束在自由空间中非傍轴传输的解析表达式,并与傍轴的情况进行了对比.研究表明:f参数、离轴系数和传输距离对径向偏振高斯光束的非傍轴传输特性有着重要的影响,而且,传输距离较远,离轴径向偏振光束的光斑向光轴靠拢,表现出较强的离轴修复能力.这些结论在多束离轴激光束进行光束合成和光束整形的研究中具有重要意义.
离轴径向偏振光束; 离轴量;f参数; 矢量瑞利-索末菲衍射积分; 非傍轴传输特性
径向偏振光束具有沿光轴对称的偏振分布以及中空的圆环形光束结构,在光束传输和大数值孔径聚焦过程中,具有更独特的优点.例如:径向偏振光通过大数值孔径透镜聚焦可以产生比线偏振光更小的光斑,有效地提高成像系统的空间分辨率[1-2].此外,聚焦的径向偏振光束可以产生比线偏振光更大的梯度力,不产生轴向的散射力在光学捕捉中有重要应用[3-5].因此,径向偏振光束的产生和传输引起了研究人员的极大关注[6-11]. 将径向偏振光和贝塞尔高斯光束的无衍射特性结合起来,在实验上可获得径向偏振无衍射光束[12].研究部分相干径向偏振光束的自修复特性表明,径向偏振贝塞尔高斯光束具有比线偏振贝塞尔高斯光束更好的自修复能力[13]. 径向偏振光束也被扩展到部分相干光领域.
当光束的光斑尺寸很小(与波长相近)或远场发散角很大,傍轴理论则不再有效,需要用更为严格的矢量波动方程理论来研究非傍轴光束的行为.非傍轴光束可以通过半导体激光器或大数值孔径聚焦系统产生.利用矢量瑞利-索末菲衍射积分法研究表明,径向偏振光束在自由空间和经圆形孔中具有非傍轴传输特性[14-16].而在实际光学系统中由于受到外部因素和系统结构等因素的影响,径向偏振光束的中心轴线往往与光学系统光轴有一定偏离[17].另一方面,实际工作中,通常使用多束离轴激光束进行光束合成,因此对离轴偏振光束在非傍轴领域的研究显得很有必要[18].本文基于矢量瑞利-索末菲衍射积分公式,对离轴径向偏振TEM01模式光束在自由空间中的非傍轴传输特性进行了系统研究,并与傍轴的情况进行了对比.
1 理论分析
在直角坐标系中,离轴径向偏振TEM01模式光束在z=0平面上可表示为[19]:
[(x0-a)i+(y0-b)j],
(1)
其中,w0为径向偏振光束在x、y轴方向上的束腰宽度,a、b为x、y轴方向上的离轴参数,i、 j分别为x、y轴方向的单位矢量.在x、y轴方向上:
Ex(x0,y0,0)=
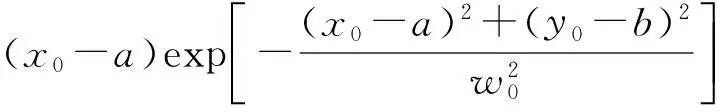
(2)
Ey(x0,y0,0)=
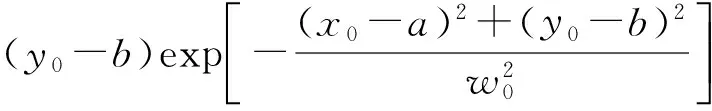
(3)
(4)
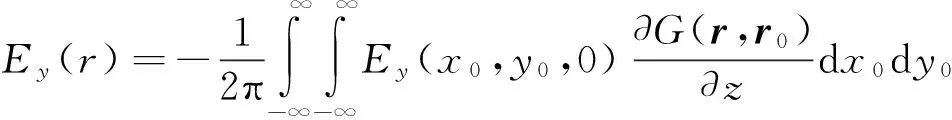
(5)
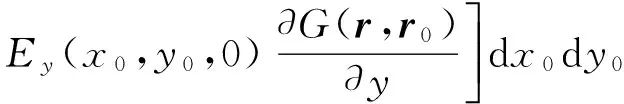
(6)
其中r0=x0i+y0j,r=xi+yj+zk,k为z方向的单位矢量,而G(r,r0)可表示为:
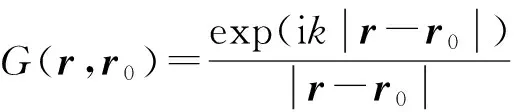
(7)
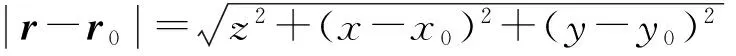
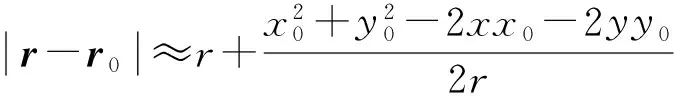
(8)
将式(7)、(8)带入式(6),可得瑞利-索末菲衍射积分的非傍轴近似形式:
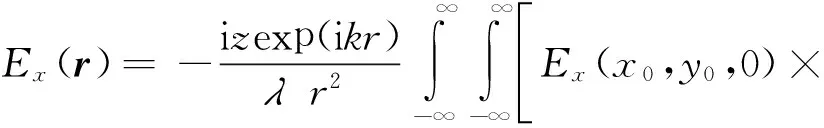
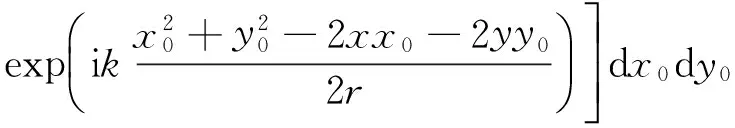
(9)
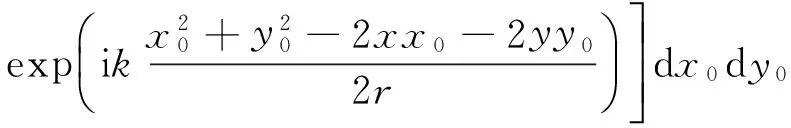
(10)
Ey(x0,y0,0)(y-y0))×
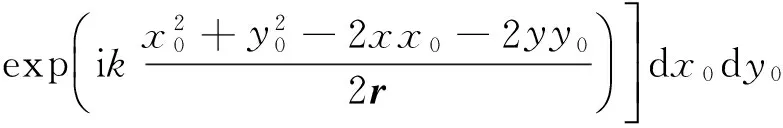
(11)
将式(2)、(3)带入式(11),经过积分可得非傍轴情况下的光场解析表达式[21]:
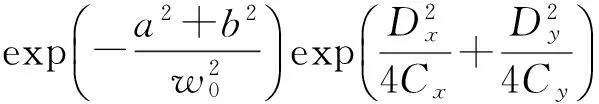
(12)
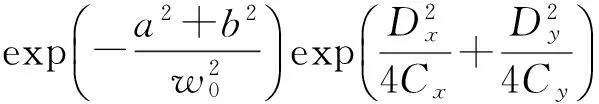
(13)
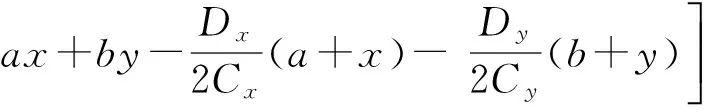
(14)
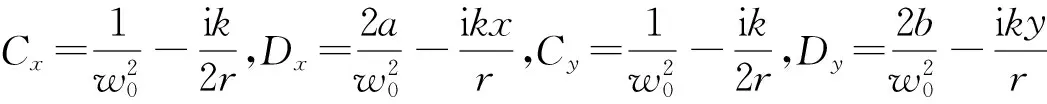
式(14)描述了径向偏振离轴高斯光束在自由空间的非傍轴传输规律,它对远场和近场都适用,令a=0,b=0, 则其表示非离轴的径向偏振光束的非傍轴传输表达式,这和文献[14]1230的式(16)~(18)一致,是本文的主要解析结果.
在远场情况下,式(8)可以进一步写为:
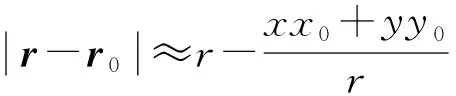
(15)
将式(2)、(3)、(7)、(15)代入式(6),经过积分可得远场条件的解析表达式:
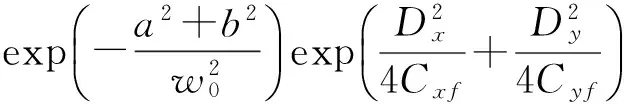
(16)
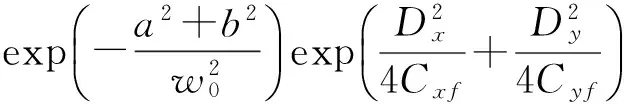
(17)
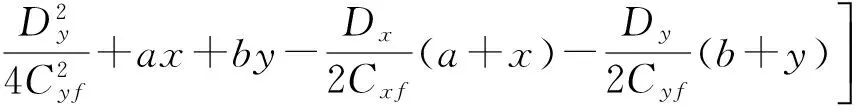
(18)
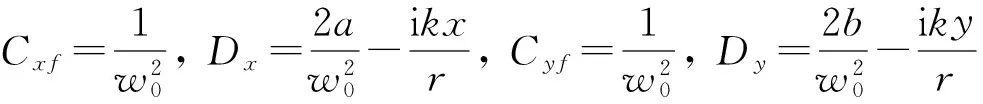
对于傍轴光束,将式(12)~(14)和式(16)~(18)的exp(ikr)的r作傍轴近似:
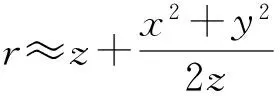
(19)
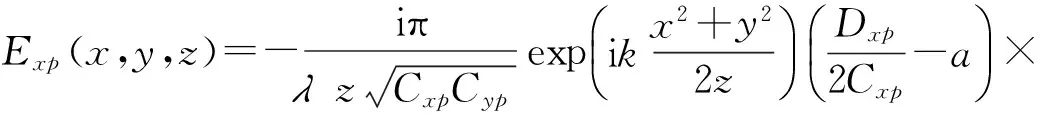
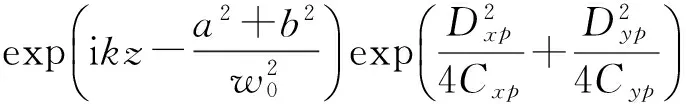
(20)
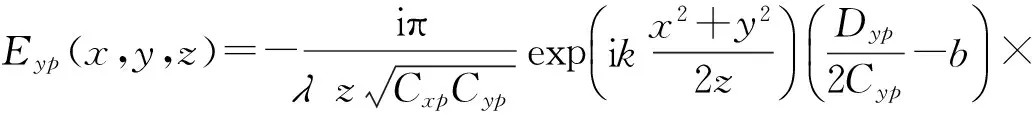
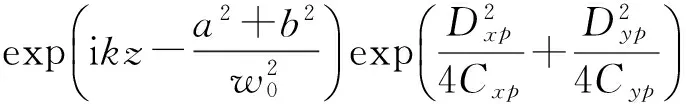
(21)
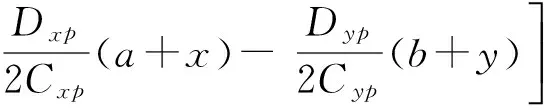
(22)

令a=0,b=0,则式(20)~(22)表示径向偏振光束的傍轴传输表达式,和文献[22]中的式(26)和(29)的计算结果一致.

对非傍轴解析式(12)~(14)中的关键项进行如下计算:
(23)
(24)
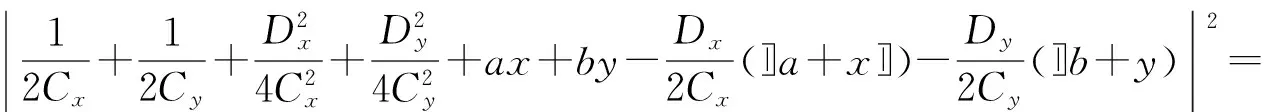
(25)
其中,f=1/kw0,*为复共轭.
由式(23)可知横向光场分布Ix+Iy在x=a,y=b处始终为0,结合式(24),由于的存在当传输距离z越大,Ix+Iy的分布越接近圆环状,其相应的圆心越靠近(a,b),而当z较小时,Ix+Iy、Iz的分布呈现出不规则的形状,即出现畸变,并且在(0,b)处的光强要比(2a,b)处的强,可得出此时圆环上的最大光强将出现在偏移量相反方向.同理从式(25)可以看出,Iz在中心(a,b)处的光强不为0,结合式(24)可知,当z较小时式(24)对Iz的影响较大,当z较大时式(25)对Iz的影响较大,因此随着z的增大,Iz的分布会呈现出从圆斑到圆环的变化.从式(23)和式(25)不难看出,参数f越小Iz对Inp的影响越小.
对于傍轴解析表达式(20)~(22)中的关键项只需要将式(23)~(25)中的r用z替换即可.
(26)
(27)
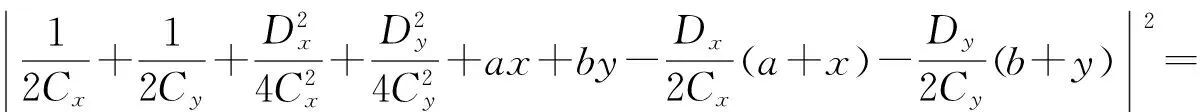
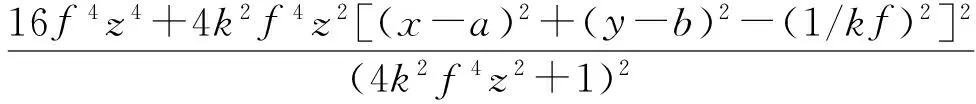
(28)
对比式(23)~(25)和式(26)~(28),发现式(23)~(25)中存在4k2f4r2(r2=x2+y2+z2)项,当f越大,傍轴光强和非傍轴的差别越大,而z越大傍轴和非傍轴的差别越小.
2 结果与讨论
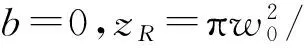
图1表明,当a=0时,Ip、Inp、Ix+Iy和Iz的光斑分布呈中心对称分布,而且Inp和Ip没有差别,此时非傍轴径向偏振高斯光束的特性可以用傍轴近似来分析.随着a从0增加到4λ的过程中,Ip(x,y,zR)与Inp(x,y,zR)的差别逐渐增加,这说明了离轴量导致了光束的非傍轴性,此时傍轴近似不能很好地说明离轴径向偏振光束的特性,因此,非傍轴近似是必须的. 而且随着a从0逐渐变化至4λ过程中,Ip、Inp、Ix+Iy和Iz的光斑分布偏离光轴,Ip、Inp、Ix+Iy和Iz的光斑中心沿x轴偏移原点的距离随着a的增加而增加;而且Inp(x,y,zR)、Ix+Iy(x,y,zR)失去对称性,但仍为圆环状,光强最大值出现在圆环右边,a越大圆环上光强最小值越小.图1D~N表明,a从0变化至4λ的过程中,Ip(x,y,zR)与Iz(x,y,zR)未有出现明显的畸变.
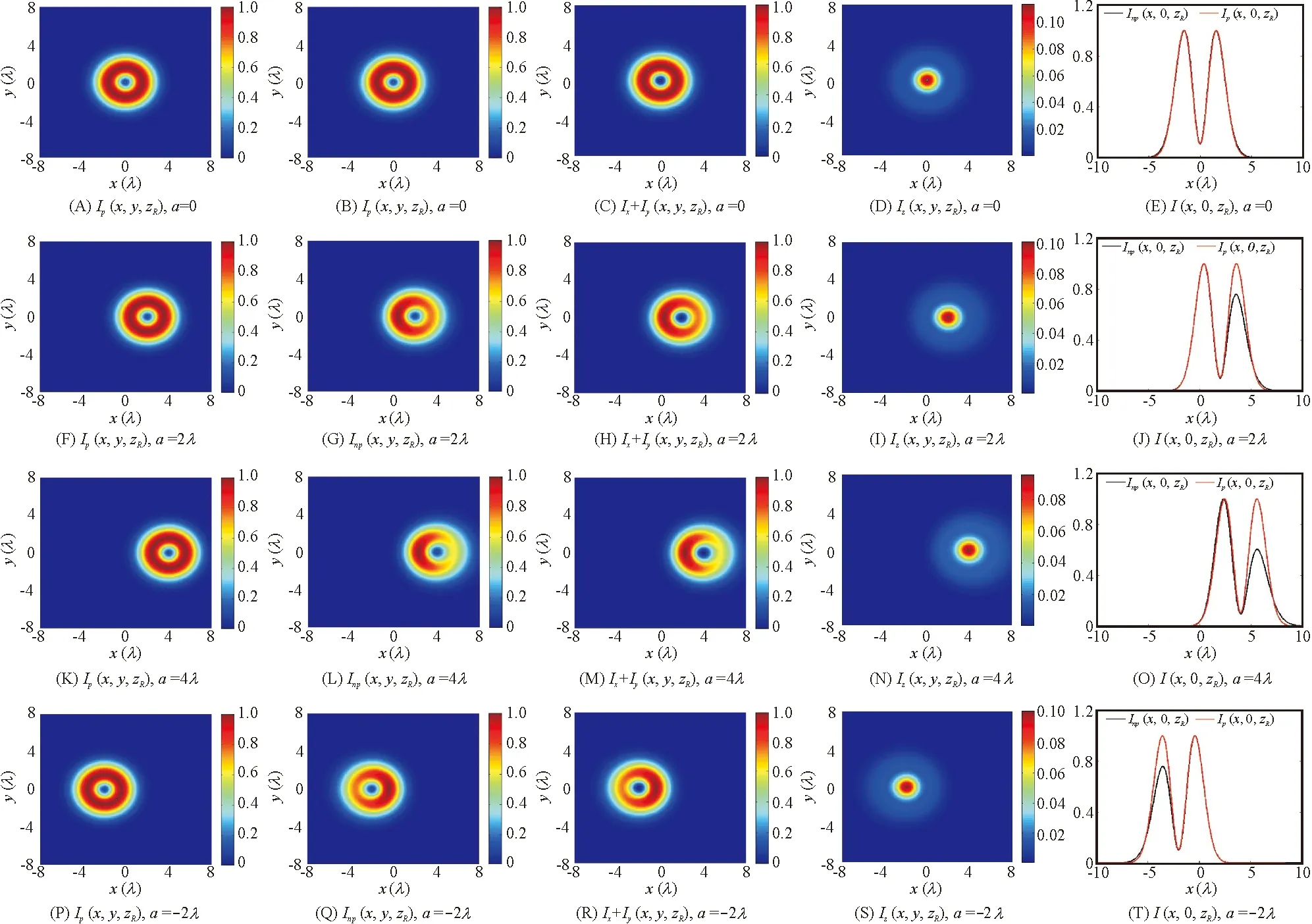
图1 Ip、Inp、Ix+Iy和Iz的分布随离轴量a的模拟图及其x轴向分布曲线(f=0.1, z=zR)
Figure 1Simulated diagrams andxaxial distribution curves ofIp,Inp,Ix+IyandIzvarying with off-axis coefficienta(f=0.1,z=zR)
图2表示在z=10zR处,Ip、Inp、Ix+Iy和Iz的归一化光强分布.其中,f=0.1,a=0、2λ、4λ、-4λ.在z=10zR处,随着a从0增加到4λ的过程中,Ip与Inp差别很小,当离轴量a小于4λ,Ip与Inp差别可忽略,表明在传输距离较远处,离轴量a对光束的非傍轴性的影响减弱,在离轴量很小,非傍轴径向偏振高斯光束的特性可以用傍轴近似来分析.而且在z=10zR处,Ip、Inp、Ix+Iy、Iz的光强分布仍具有对称性,Ip、Inp、Ix+Iy、Iz的光斑分布向光轴靠拢,这说明,传输距离较远时,离轴径向偏振光束的表现出较强的离轴修复能力.
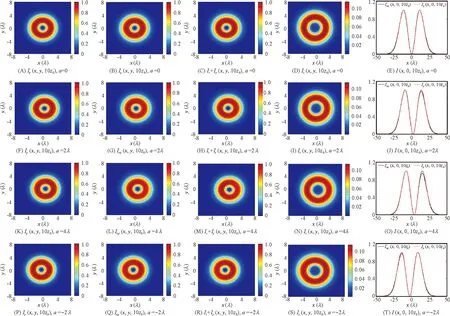
图2 Ip、Inp、Ix+Iy和Iz的分布随离轴量a的模拟图及其x轴向分布曲线(f=0.1,z=10zR)
图3和图4表明,当f=0.1、a=0时,Inp、Ix+Iy、Iz存在差别,因为随着f参数的增加,即光束的发散性增强,导致光束的非傍轴效应增强,从而导致傍轴光强和非傍轴的光强差异增大.此外,在a从0逐渐变化至λ的过程中,Inp和Ip的差别进一步增大,而且Inp、Ix+Iy、Iz沿x轴正方向偏移原点较小距离并出现畸变,a越大,光斑偏移原点距离越大,畸变越严重.但随着传输距离z的增加,光斑向光轴靠拢,光斑畸变逐渐减小,光斑的变化呈现出规律性.
f参数、离轴量a和传输距离共同决定着离轴径向偏振光束的非傍轴传输特性(图1~4).f越大,传输距离z越小,离轴量a越大,Ip和Inp的差异越大,光束的非傍轴效应越强.此外,f参数、传输距离z和离轴量a对非傍轴离轴径向偏振光束的光斑演化起着重要的影响,通过改变f参数、离轴量a和传输距离,可以调节离轴径向偏振光束的光斑分布.
3 结论
对离轴径向偏振TEM01模式光束在自由空间中的非傍轴传输做了详细研究,推导了离轴径向偏振光束在自由空间中非傍轴传输的解析表达式,并根据解析表达式分析了非傍轴离轴径向偏振光束传播特性.离轴径向偏振光束在远场以及傍轴传输可作为本文的2种特例.数值结果表明:f参数、离轴参数a和传输距离z共同决定离轴径向偏振光束的非傍轴行为,它们对光强的分布影响很大,而且对光强分布的影响不同.随着f参数的增大,傍轴和非傍轴的差异增加.随着离轴量a的增加,傍轴和非傍轴的光斑分布偏离光轴而且发生畸变.但随着传输距离z的增加,傍轴和非傍轴的差异减小,光斑畸变减小,光强分布向光轴靠拢,表现出较好的离轴修复能力,其模拟结果和理论分析一致.研究结果可用在非傍轴径向偏振光束的光束合成和光束整形方面.
图3Ip、Inp、Ix+Iy和Iz的分布随离轴量a的模拟图及其x轴向分布曲线(f=0.5,z=zR)
Figure 3Simulated diagrams andxaxial distribution curves ofIp,Inp,Ix+IyandIzvarying with off-axis coefficienta(f=0.5,z=zR)
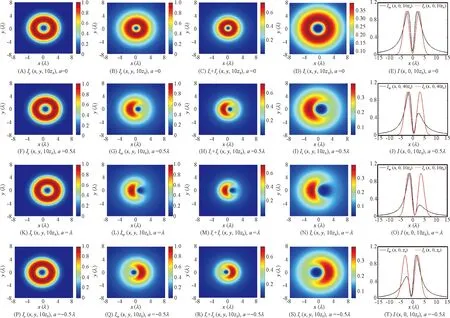
图4 Ip、Inp、Ix+Iy和Iz的分布随离轴量a的模拟图及其x轴向分布曲线(f=0.5,z=10zR)
[1]KANO H. Excitation of surface-plasmon polaritons by a focused laser beam[J]. Journal of the Optical Society of America B, 1998, 15(4):1381-1386.
[2]KOUYOU W, NOBUHIRO H, HIROSHI K. Optimized measurement probe of the localized surface plasmon microscope by using radially polarized illumination[J]. Applied Optics, 2007, 46(22):4985-4990.
[3]KUGA T, TORII Y, SHIOKAWA N, et al. Novel optical trap of atoms with a doughnut beam[J]. Physical Review Letters, 1997, 78(25):4713-4716.
[4]GAHAGAN K T, SWARTZLANDER G A. Simultaneous trapping of low-index and high-index micro particles observed with an optical-vortex trap[J]. Journal of the Optical Society of America B,1999,16(4):533-537.
[5]ZHAN Q W. Trapping metallic Rayleigh particles with radial polarization[J]. Optics Express, 2004, 12(15):3377-3382.
[6]LI J L,UEDA K, MUSHA M, et al. Radially polarized and pulsed output from passively Q-switched Nd:YAG ceramic microchip laser[J]. Optics Letters, 2008, 33(22):2686-2688.
[7]ZHAN Q W. Cylindrical vector beams: from mathematical concepts to applications[J]. Advances in Optics & Photonics, 2009, 1(1):1-57.
[8]GROSJEAN T, COURJON D, SPAJER M. An all-fiber device for generating radially and other polarized light beams[J]. Optics Communications, 2002, 203(1/2):1-5.[9]林惠川,刘辉,蒲继雄. 腔外相干叠加产生径向偏振光[J]. 中国激光,2009,36(s1):251-256.LIN H C,LIU H,PU J X. Extra cavity coherent superposition for generation of radially polarized beam[J].Chinese Journal of Lasers,2009,36(s1):251-256.
[10]张艳丽,李小燕,朱健强. 矢量偏振光束的产生及其高数值孔径聚焦性质[J]. 中国激光,2009,36(1):129-133.
ZHANG Y L,LI X Y,ZHU J Q. Generation and focusing property with high-numerical aperture lens of vectorial polarized beam[J]. Chinese Journal of Lasers,2009,36(1):129-133.
[11]黄金堂,韦玮雷,张源, 等. 利用C切钒酸钇晶体产生轴对称偏振光[J]. 光学学报,2010,30(2):557-561.
HUANG J T, WEI W L, ZHANG Y, et al. Generation of cylindrical vector beams by use of C-cut YVO4crystal[J]. Acta Optica Sinica, 2010,30(2):557-561.
[12]孙顺红,林惠川,崔省伟,等. 径向偏振无衍射光束的产生及其传输特性研究[J]. 中国科学:物理学,力学,天文学,2012,42(10):1022-1028.
SUN S H,LIN H C,CUI S W, et al. Generation and pro-pagation characteristics of the radially polarizednon-diffracting beam[J].Scientia Sinica Physica:Mechanica & Astronomica,2012,42(10):1022-1028.
[13]WU G, WANG F, CAI Y. Generation and self-healing of a radially polarized Bessel-Gauss beam[J]. Physical Review A, 2014, 89(4):8821-8822.
[14]DENG D. Nonparaxial propagation of radially polarized light beams[J]. Journal of the Optical Society of America B, 2006, 23(6):1228-1234.
[15]阎杰,鲁拥华,王沛,等. 径向偏振光聚焦光斑研究[J]. 光学学报,2010,30(12):3597-3603.YAN J,LU Y H, WANG P, et al. Study of focal spot of radially polarized beam[J].Acta Optica Sinica,2010,30(12):3597-3603.
[16]GUO L N,TANG Z L,WANG J. Non-paraxial propagation of cylindrical vector vortex beams in the far-field[J]. Chinese Physics Letter,2014, 31(7):85-89.
[17]WEI M D, CHANG K C, LIN T. Azimuthally and radially polarized off-axis lasers[J]. SPIE Newsroom, 2013,doi:10.1117/2.1201310.005143.[18]高曾辉,吕百达. 矢量非傍轴离轴高斯光束的传输[J]. 物理学报,2005,54(11):5144-5148.
GAO Z H, LV B D. Propagation of vectorial off-axis Gaussian beams beyond the paraxial approximation[J]. Acta Physica Sinica, 2005,54(11):5144-5148.
[19]李杨,朱竹青,王晓雷,等. 离轴椭圆矢量光场传输中的光斑演变[J]. 物理学报,2015,64(2):Art 024204,8pp.
LI Y, ZHU Z Q, WANG X L, et al. Propagation evolution of the off-axis ellipse vector beam[J]. Acta Physica Sinica, 2015,64(2): Art 024204,8pp.
[20]LUNEBURG R K. Mathematical theory of optics[J]. American Journal of Physics, 1966, 34(1):320.
[21]ABRAMOWITZ M, STEGUN I, MCQUARRIE D A. Handbook of mathematical functions[J]. American Journal of Physics, 1966, 34(2):177.
[22]RICCARDO B, MASSIMO S. Nonparaxial propagation of spirally polarized optical beams[J]. Journal of the Optical Society of America:A Optics Image Science & Vision, 2004, 21(10):2032.
【中文责编:成文英文责编:肖菁】
Nonparaxial Propagation Properties of Off-Axis Radially Polarized Beams
NI Bo1, GUO Lina2, WU Yongbo1,TANG Zhilie1*
(1.School of Physics and Telecommunication Engineering, South China Normal University, Guangzhou 510006, China;2.School of Electronics and Information, GuangDong Polytechnic Normal University, Guangzhou 510665, China)
Based on the vectorial Rayleigh-Sommerfeld diffraction formula, the analytical expressionons for nonparaxial off-axis radially polarized Gaussian beams propagating in free space are derived. The nonparaxial propagation properties of off-axis radially polarized Gaussian beams are studied, and compared with the corresponding paraxial results. It is shown that the f parameter, off-axis coefficient and propagation distance play important roles in the nonparaxial propagation properties of the off-axis radially polarized Gaussian beams. Moreover, when the propagation distance is farther, the off-axis radially polarized beams exhibit better off-axis healing property.
off-axis radially polarized beams; off-axis coefficient;fparameter; vectorial Rayleigh-Sommerfeld diffraction integral; nonparaxial propagation property
2015-09-19《华南师范大学学报(自然科学版)》网址:http://journal.scnu.edu.cn/n
国家自然科学基金项目(61178086,11404067);中国博士后科学基金项目(2015M570473)
唐志列, 教授, Email: tangzhl@scnu.edu.cn.
O436.1
A
1000-5463(2016)03-0075-07

