A Framework for Semantic Similarity Estimation in Formal Concept Analysis

JIANG Yuncheng, LI Pu, Akram AFTAB

(School of Computer Science, South China Normal University, Guangzhou 510631, China)



A Framework for Semantic Similarity Estimation in Formal Concept Analysis

JIANG Yuncheng*, LI Pu, Akram AFTAB

(School of Computer Science, South China Normal University, Guangzhou 510631, China)

To realize the semantic similarity estimation for Formal Concept Analysis (FCA) concepts or concept lattices, the formal contexts of FCA are extended into semantic cases by using the concepts of Description Logics (DLs) to act as the attributes of formal contexts, that is, a kind of semantic representation for formal contexts is presented using domain ontologies (DL knowledge bases). Furthermore, a framework for semantic similarity estimation of FCA concepts and concept lattices by using DL reasoning (i.e., ontology reasoning) is proposed based on the semantic representation for formal contexts. The framework ensures that the semantic similarity measures resulting from instantiations fulfill fundamental properties such as symmetry and equivalence invariance.

formal concept analysis; semantic similarity; description logics

Chinese library classification：TP391Document code：AArticle ID: 1000-5463(2016)03-0044-09

Formal Concept Analysis (FCA) has been introduced by WILLE[1]in 1982 for analyzing and structuring a domain of interest[1-2]. It is not only a method for data analysis and knowledge representation, but also a formal formulation for concept formation and learning[3]. In fact, FCA is a conceptual clustering technique that formalizes the concept of ‘concept’ as established in the international standard ISO 704 (a concept is considered as a unit of thought constituted of two parts: its extent and its intent[1-2]).

FCA starts with the notion of a formal context specifying, which objects have what attributes. From a semantics point of view, a formal context is an information system which contains values 0 or 1[3]. It is based on the perspective that a concept has two constituent parts: its extent, which consists of all objects belonging to the concept, and its intent, which comprises all attributes shared by the objects. An important notion in FCA is thus a formal concept, which is a pair consisting of a set of objects (the extents) and a set of attri-butes (the intents) such that the intent consists of exactly those attributes that the objects in the extent have in common, and the extent contains exactly those objects that share all attributes in the intent. All concepts associated with the formal context form a complete lattice called the concept lattice.

As pointed out by ALQADAH and BHATNAGAR[4], one shortcoming of FCA is the large number of formal concepts that typically arise in dense datasets hindering typical tasks such as rule generation and visualization. To overcome this shortcoming, it is important to develop formalisms and methods to segment, categorize and cluster formal concepts. The first step in achieving these aims is to define suitable similarity and dissimilarity measures of formal concepts. A similarity measure of formal concepts is used for estimating the degree of similarity between two formal concepts. Seve-ral researchers like ALQADAH and BHATNAGAR[4], BELOHLAVEK[5], TADRAT et al.[3], and FORMICA[6-8]have worked on similarity measures of formal concepts in FCA.

It is worth noting that all these studies mentioned above in similarity measures do not consider semantic representation of attributes of formal contexts (or formal concepts, concept lattices). Thus, the approaches of measuring the similarity between FCA concepts mentioned above cannot use the implicit knowledge between attributes deduced from explicitly represented knowledge (i.e., attributes). That is, the existing methods of similarity measures of FCA concepts only make use of the explicitly represented attributes of formal contexts (or formal concepts). It is easy to know that the attributes in formal contexts are very simple. Each attribute is only a word or a term, and expressive (or complex) attributes are not considered in formal contexts. Similarly to the parameters of soft sets[9-11], the attributes of formal contexts have not semantics from a semantic point of view. Therefore, the existing methods of similarity measures of FCA concepts cannot eva-luate similarity of FCA concepts at the semantic level.

It is well known that ontologies provide a formal specification of a shared conceptualization. Thanks to initiatives such as the Semantic Web, which brought the creation of thousands of domain ontologies, ontologies have been extensively exploited in knowledge-based systems[12]. The Web Ontology Language which comprises three sublanguages of increasing expressive power: OWL Lite, OWL DL and OWL Full, and its revision OWL 2, are well-known languages for ontology modeling. Nowadays, properties and semantics of ontology constructs mainly are determined by Description Logics (DLs)[13], which can be used to represent the terminological knowledge of an application domain in a structured and formally well-understood way. DL systems provide their users with inference services that deduce implicit knowledge from the explicitly represented knowledge.

To assess similarity between FCA concepts at the semantic level, in this paper we will propose a framework for semantic similarity estimation of FCA concepts (or concept lattices) by using DL reasoning (i.e., ontology reasoning) that can deduce implicit knowledge from the explicitly represented knowledge.

1　Preliminaries

1.1Description Logics

C∷=·|A|CD|r.CwhererNRandC,Ddenote arbitrary εL-concepts.

An interpretationI=(ΔI, •I) consists of a domain of interpretationΔI, and an interpretation function •Imapping every atomic conceptAto a subset ofΔIand every atomic roleRto a subset ofΔI×ΔI. The top-concept · is mapped toΔI. The interpretation function •Iis extended to complex concepts of εL as follows:(CD)I=CI＿DIand (r.C)I={xΔI|yΔI,x,yrI∧yCI}.

We callA=Ca concept definition andACa primitive concept definition. A finite set of (possibly primitive) concept definitions is a TBox TB. A concept nameAis called a primitive name of TB, iff it does not occur on the left-hand side of any concept axiom in TB. The set of all primitive names in denoted asNB.

1.2Formal Concept Analysis

Definition 3A formal concept (or FCA concept) of the formal contextK=(G,M,J) is a pair (A,B) withAíG,BíM,A′=BandB′=A. We callAthe extent andBthe intent of the formal concept (A,B). B(G,M,J) (or B(K)) denotes the set of all formal concepts of the formal contextK=(G,M,J), Int(K) and Ext(K) denote the sets of intents and extents of all formal concepts of the formal contextK=(G,M,J), respectively.

We have the following properties: if (G,M,J) is a context,A,A1,A2íGare sets of objects andB,B1,B2íMare sets of attributes, then:(1)A1íA2ííB2ííA″,BíB″; (3)A′=A‴,B′=B‴; and (4)AíB′BíA′A×BíJ.

2　Semantic Representation of Formal Contexts Based on DLs

2.1Semantic Representation of Formal Contexts

Definition 5LetK=(G,M,J) be a formal context, whereG={a1,…,am},M={C1,…,Cn}. Suppose that DO=〈RB,TB〉 is a domain ontology (i.e., DL-ontology) expressed in εLH, where TB is an unfoldable TBox, andΣis the set of all εLH-concepts of TB in DO (denoted byC(εLH,DO)), i.e.,Σ=C(εLH, DO). IfMíΣ, then 〈K,DOAB〉 is called as a se-mantic representation ofKw.r.t. DO, where DOAB=〈RB,TB,AB〉, AB={Ci(aj)|ajG,CiM,(aj,Ci)J}.

Clearly, if we only consider the definition of semantic representation of formal contexts, we can use an arbitrary (decidable) description logic. The semantic representation of several formal contexts may also be defined as follows: LetK1=(G1,M1,J1),…,Kn=(Gn,Mn,Jn) be some formal contexts, whereG1={a11,…,a1m},…,Gn={an1,…,anm},M1={C11,…,C1m},…,Mn={Cn1,…,Cnm}. Suppose that DO=〈RB,TB〉 is a domain ontology (i.e., DL-ontology) expressed in εLH, where TB is an unfoldable TBox, andΣis the set of all εLH-concepts of TB in DO, i.e.,Σ=C(εLH, DO). IfMiíΣ(1≤i≤n), then 〈K1…Kn,DOAB〉 is called as a semantic representation ofK1,…,Knw.r.t. DO, where DOAB=〈RB,TB,AB〉,AB={Cij(akl)|aklG1…Gn,CijM1…Mn,(akl,Cij)J1…Jn}.

The εLH-ontology of a semantic representation 〈K,DOAB〉 ofKw.r.t. DO uses an open-world semantics. The formal context of a semantic representation has a closed-world semantics. In fact, we only use open-world assumption in subsumption reasoning of DO=〈RB,TB〉. In formal contexts of FCA and AB of εLH-ontology of a semantic representation,we require closed-world knowledge about objects, thus, from a DL viewpoint we may use a model as a closed-world representation of objects.

The algorithm of constructing a semantic representation is as follows.

Algorithm 1Construct the semantic representation of formal context

Input: a formal contextK=(G,M,J), whereG={a1,…,am},M={C1,…,Cn}

Output: a semantic representation 〈K,DOAB〉 ofKw.r.t. DO, where DOAB=〈RB,TB,AB〉

(1) 〈RB,TB,AB〉:=φ,i.e.,RB:=φ,TB:=φ, and AB:=φ;

(5) RB:=RIA(role(TB)), DO:=〈RB,TB〉;

(7) return 〈K,DOAB〉.

2.2Conflict Management

Definition 6LetK=(G,M,J) be a formal context, DO=〈RB,TB〉 be a domain ontology (i.e., DL-ontology) expressed in εLH, and 〈K,DOAB〉 be the semantic representation ofKw.r.t. DO. There exists a conflict(C1,C2,a) inKw.r.t. DO iff both of the following conditions hold:

To implement the conflict resolution of a formal context (i.e., obtain a correct context), we have to find all conflicts in formal context. The approach is as follows:

Algorithm 2Find all conflicts in formal context (i.e., conflict detection algorithm)

Input: a formal contextK=(G,M,J) whereG={a1,…,am},M={C1,…,Cn}, a semantic representation 〈K,DOAB〉 ofKw.r.t. DO where DO=〈RB,TB〉

Output: The set conflicts(K,DO) of all conflicts inKw.r.t. DO

conflicts(K,DO):=φ

for all attributes {C1,…,Cn} inMdo

for all objects {a1,…,am} inGdo

if (1) there existCiandCj(1≤i,j≤n) such that DOCiCj, and

endfor

endfor

Now we give the method to conflict resolution for formal contexts.

Algorithm 3Remove all conflicts for formal context (i.e., conflict resolution algorithm)

Input: a formal contextK=(G,M,J), whereG={a1,…,am},M={C1,…,Cn}

Output: a correct formal contextK′=(G,M,I) which does not include conflicts

(1)I:=J;

(2) use Algorithm 1 to obtain a semantic representation 〈K,DOAB〉 ofK;

(3) utilize Algorithm 2 to get the set conflicts(K,DO) of all conflicts inKw.r.t. DO;

(5) returnK′=(G,M,I).

3　Semantic Representation of Formal Contexts Based on DLs

3.1Semantic Similarity for Formal Concepts

The mathematical metric space is a pair (D,d), where D is the domain of objects anddis the distance functiond:D×D →+{0} able to compute distances between any pair of objects from D. From a normalized metric space (D,d), we can define a similarity functions: D ×D →[0,1] by definings(X,Y)=1-d(X,Y) for allX,YD. Formally

(1)s(X,Y)=1X=Yidentity of indiscernible,

(2)s(X,Y)=s(Y,X) symmetry,

(3)1+s(X,Y)≥s(X,Z)+s(Z,Y) triangle inequality.

Definition 8LetK1=(G1,M1,J1),…,Kn=(Gn,Mn,Jn) be some formal contexts. Given any two formal concepts (EX1,IN1) and (EX2,IN2) of the same formal contextKi(or different formal contextsKi,Kj), a similarity measure sim between (EX1,IN1) and (EX2,IN2), denoted as sim((EX1,IN1),(EX2,IN2)), is a function:

sim: B(Gi,Mi,Ji)×B(Gi,Mi,Ji)→[0,1]

(or sim: B(Gi,Mi,Ji)×B(Gj,Mj,Jj)→[0,1])

such that sim((EX1,IN1),(EX2,IN2))=sim((EX2,IN2),(EX1,IN1)).

Now we present simcon, a framework for similarity measures for formal concepts (i.e., FCA concepts) based on extent similarity and intent similarity.

Definition 9LetK1=(G1,M1,J1),…,Kn=(Gn,Mn,Jn) be some formal contexts. Given any two formal concepts (EX1,IN1) and (EX2,IN2) of the same formal contextKi(or different formal contextsKi,Kj), the similarity of EX1and EX2, denoted as simext(EX1,EX2), is a function:

simext: Ext(Ki)×Ext(Ki)→[0,1]

(or simext: Ext(Ki)×Ext(Kj)→[0,1])

such that simext(EX1,EX2)=S(EX1,EX2), whereSis the Jaccard index, Sorenesen coefficient, or Symmetric difference.

According to the properties of Jaccard index, Sorenesen coefficient, or Symmetric difference[4]249, we know that the similarity of extents of FCA concepts satisfies the property of symmetry, i.e., simext(EX1,EX2)=simext(EX2,EX1).

To implement semantic similarity measures for FCA concepts, we have to use the similarity measures for DL concepts. In this paper we will use the approaches presented in References [14-15] to measure similarity of DL concepts because the framework provides the flexibility to adjust measures to specifics of the modeled domain.

Definition 10Let DO=〈RB,TB〉 be a domain ontology (i.e.,DL-ontology) expressed in εLH,K1=(G1,M1,J1),…,Kq=(Gq,Mq,Jq) be some formal contexts, and 〈K1…Kq,DOAB〉 be a semantic representation ofK1,…,Kqw.r.t. DO. Given two setsM1={C1,C2,…,Cm} andM2={D1,D2,…,Dn} (m≤n) of attributes (i.e., εLH-concepts) of the same formal contextKi(or different formal contextsKi,Kj), if there is a mappingf:M1→M2such that

(2)Ck≠Clf(Ck)≠f(Cl),

Now we present simint, a similarity measure for intents of FCA concepts. Similarly to the framework for DL concepts[14-15], simint also uses unfoldable TBox.

If two intents IN1and IN2are logical equivalent w.r.t. DO (i.e., IN1≡DOIN2), then we should have simint(IN1,IN2)=1 from a semantics point of view. Since IN1≡DOIN2iff IN1DOIN2and IN2DOIN1(see Definition 10), so we can define simint by extending similarity measure for DL concepts[14-15]. Formally, for any two intents IN1and IN2,

simint(IN1,IN2)=

simintd(IN1,IN2)simintd(IN2,IN1),

where simintd(IN1,IN2) stands for directed similarity of IN1and IN2, and is defined as simintd(IN1,IN2)=1 iff IN2DOIN1, andis a fuzzy connector such as boundedt-norms, the Dice’s connector, or the average introduced in References [14-15]. The definition of fuzzy connector is as follows:

Definition 11[14]63A fuzzy connector is an opera-tor on the interval [0,1],:[0,1]×[0,1]→[0,1] such that for allx,y[0,1] the following properties are true:

• commutativity:xy=yx,

• equivalence closed:xy=1x=y=1,

• weak monotonicity:x≤y1x≤1y,

• bounded:xy=0x=0 ory=0, and

Now we present the definition of simintd. The notion of simintdpresented below is based on maximum weighted matching problem in bipartite graphs[6-7].

∀k,l≠h}.

Definition 13Let DO=〈RB〉 be a domain ontology expressed in εLH,K1=(G1,M1,J1),…,Kq=(Gq,Mq,Jq) be some formal contexts, and 〈K1…Kq,DOAB〉 be a semantic representation ofK1,…,Kqw.r.t. DO. Given any two formal concepts (EX1,IN1) and (EX2,IN2) of the same formal contextKi(or different formal contextsKi,Kj), where IN1={C1,C2,…,Cm} and IN2={D1,D2,…,Dn}, the directed similarity of IN1and IN2, denoted as simintd(IN1,IN2), is the function simintd: Int(K)×Int(K)→[0,1], and is defined as follows:

simid(Ci,Dj)=

where:

(1)thefunctionρ:C(εLH)→P(NA) is defined in Section 1.1,

(2)A is a boundedt-conorm,

(3)the functiong:NA→+is a weighting function,

(4)the functionp:(NC×NC)(NR×NR)→[0,1] is a primitive measure,

Definition 14[14]60A functiong:NA→+is called a weighting function. The functiongdef:NA→+with for allC′NA,gdef(C″)=1, is called the default weighting function.

Definition 15[14]55A functionp:(NC×NC)(NR×NR)→[0,1] with the properties that for allA,BNCandr,s,tNR

•p(A,B)=1A=B,

•p(r,s)=1sr,

•sRBrp(r,s)>0, and

•tRBsp(r,s)≤p(r,t),

is called a primitive measure.

Therefore, for any two formal concepts (EX1,IN1) and (EX2,IN2) of the same formal contextKi(or different formal contextsKi,Kj), we have that the simi-larity simint(IN1,IN2) of IN1and IN2is as follows, where IN1={C1,C2,…,Cm} and IN2={D1,D2,…,Dn}:

simint(IN1,IN2)=

simintd(IN1,IN2)

Theorem 1Let DO=〈RB〉 be a domain ontology expressed in εLH,K1=(G1,M1,J1),…,Kq=(Gq,Mq,Jq) be some formal contexts, and 〈K1…Kq,DOAB〉 be a semantic representation ofK1,…,Kqw.r.t. DO. For any formal concepts (EX1,IN1),(EX2,IN2), and (EX3,IN3) of the same formal contextKi(or different formal contextsKi,Kj,Kk),

(1)simint(IN1,IN2)=simint(IN2,IN1), i.e., simint fulfills symmetry;

(2)if IN1≡DOIN2, then we have that simint(IN1,IN3)=simint(IN2,IN3), i.e., simint fulfills equivalence invariance.

Now we present the similarity simcon of two formal concepts by using extent similarity (i.e.,simext) and intent similarity (i.e., simint).

Definition 16Let DO=〈RB〉 be a domain ontology expressed in εLH,K1=(G1,M1,J1),…,Kq=(Gq,Mq,Jq) be some formal contexts, and 〈K1…Kq,DOAB〉 be a semantic representation ofK1,…,Kqw.r.t. DO. For any two formal concepts (EX1,IN1) and (EX2,IN2) of the same formal contextKi(or different formal contextsKi,Kj), the similarity of (EX1,IN1) and (EX2,IN2), denoted as simcon((EX1,IN1),(EX2,IN2)), is defined as follows:

simcon((EX1,IN1),(EX2,IN2))=

simext(EX1,EX2)*w+simint(IN1,IN2)*(1-w),

wherewis a weight such that 0≤w≤1, that can be established by the user to enrich the flexibility of the method.

Definition 17Let DO=〈RB〉 be a domain ontology expressed in εLH,K1=(G1,M1,J1),…,Kq=(Gq,Mq,Jq) be some formal contexts, and 〈K1…Kq,DOAB〉 be a semantic representation ofK1,…,Kqw.r.t. DO. For any formal conceptsP1=(EX1,IN1) andP2=(EX2,IN2) of the same formal contextKi(or different formal contextsKi,Kj), if EX1=EX2and IN1≡DOIN2, then we say thatP1andP2are logical equiva-lent with respect to DO (denoted byP1≡DOP2).

Theorem 2Let DO=〈RB〉 be a domain ontology expressed in εLH,K1=(G1,M1,J1),…,Kq=(Gq,Mq,Jq) be some formal contexts, and 〈K1…Kq,DOAB〉 be a semantic representation ofK1,…,Kqw.r.t. DO. For any formal conceptsP1=(EX1,IN1),P2=(EX2,IN2), andP3=(EX3,IN3) of the same formal contextKi(or different formal contextsKi,Kj,Kk),

(1)simcon(P1,P2)=simcon(P2,P1), i.e., simcon fulfills symmetry;

(2)ifP1≡DOP2, then we have that simcon(P1,P3)=simcon(P2,P3), i.e., simcon fulfills equivalence invariance.

From Theorem 2 we know that the similarity simcon of formal concepts is a similarity measure, i.e., simcon satisfies the condition (symmetry) of Definition 8. In addition, simcon also fulfills some additional property (equivalence invariance).

3.2Semantic Similarity for Concept Lattices

sim: ConLat×ConLat →[0,1]

such that

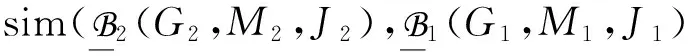
Now we present simlat, a framework for similarity measures for concept lattices based on the similarity of formal concepts.

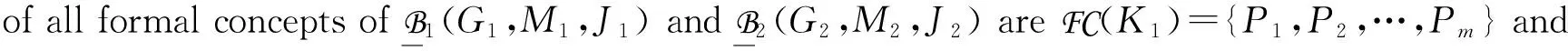
CS(FC(K2),FC(K1))={{〈Q1,P1〉,…,

∀h=1,…,m, andQh≠Qk,Ph≠Pl,∀k,l≠h}.

Definition 20Let DO=〈RB〉 be a domain ontology (i.e., DL-ontology) expressed in εLH,K1=(G1,M1,J1) andK2=(G2,M2,J2) be two formal contexts, and 〈K1K2,DOAB〉 be a semantic representation ofK1andK2w.r.t. DO.,, is the function simlat:ConLat×ConLat →[0,1], and is defined as follows:

Definition 21Let DO=〈RB〉 be a domain ontology expressed in εLH,K1=(G1,M1,J1) andK2=(G2,M2,J2) be two formal contexts, and 〈K1K2,DOAB〉 be a semantic representation ofK1andK2w.r.t. DO.y. If there is a bijective mappingf:FC(K1)→FC(K2) such that ∀PiFC(K1), there existsQj).

Theorem 3Let DO=〈RB〉 be a domain ontology expressed in εLH,K1=(G1,M1,J1),…,Kq=(Gq,Mq,Jq) be some formal contexts, and 〈K1…Kq,DOAB〉 be a semantic representation ofK1,…,Kqw.r.t. DO.y. Then

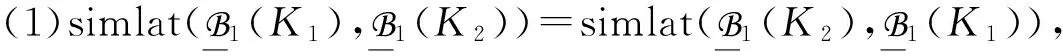
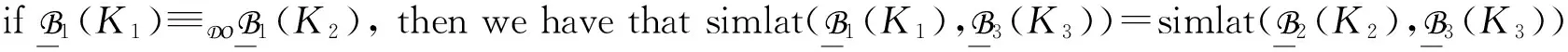
From Theorem 3 we know that the similarity simlat of concept lattices is a similarity measure, i.e., simlat satisfies the condition (symmetry) of Definition 18. In addition, simlat also fulfills some additional property (equivalence invariance).

4　Conclusion

FCA is not only a method for data analysis and knowledge representation, but also a formal formulation for concept formation and learning. DLs are a family of knowledge representation languages which can be used to represent the terminological knowledge of an application domain in a structured and formally well-understood way. In this paper, we propose a framework for semantic similarity estimation of FCA concepts or concept lattices by using DL reasoning (i.e., ontology reasoning).

[1]WILLE R. Restructuring lattice theory: an approach based on hierarchies of concepts[C]∥RIVAL I. Ordered Sets.Netherlands: Springer, 1982.

[2]GANTER B, WILLE R. Formal concept analysis: mathematical foundations[M]. Heidelberg: Springer, 1999.

[3]TADRAT J, BOONJING V, PATTARAINTAKORN P. A new similarity measure in formal concept analysis for case-based reasoning[J]. Expert Systems with Applications, 2012, 39(1): 967-972.

[4]ALQADAH F, BHATNAGAR R. Similarity measures in formal concept analysis[J]. Annals of Mathematics and Artificial Intelligence, 2011, 61(3): 245-256.

[5]BELOHLAVEK R. Similarity relations in concept lattices[J]. Journal of Logic and Computation, 2000, 10(6): 823-845.

[6]FORMICA A. Ontology-based concept similarity in formal concept analysis[J]. Information Sciences, 2006, 176 (18): 2624-2641.

[7]FORMICA A. Concept similarity in formal concept analysis: an information content approach[J]. Knowledge-Based Systems, 2008, 21(1): 80-87.

[8]FORMICA A. Similarity reasoning for the semantic web based on fuzzy concept lattices: an informal approach[J]. Information Systems Frontiers, 2013, 15(3): 511-520.

[9]HERAWAN T, DERIS M M. A soft set approach for association rules mining[J]. Knowledge-Based Systems, 2011, 24(1): 186-195.

[10]JIANG Y C, TANG Y, CHEN Q, et al. Semantic operations of multiple soft sets under conflict[J]. Computers & Mathematics with Applications, 2011, 62(4): 1923-1939.

[11]JIANG Y C, TANG Y, CHEN Q, et al. Extending soft sets with description logics[J]. Computers & Mathematics with Applications, 2010, 59(6): 2087-2096.

[12]SANCHEZ D, BATET M, ISERN D, et al. Ontology-based semantic similarity: a new feature-based approach[J]. Expert Systems with Applications, 2012, 39(9): 7718-7728.

[13]BAADER F, CALVANESE D, MCGUINNESS D, et al. The description logic handbook: theory, implementation and applications[M]. 2nd ed. New York: Cambridge University Press, 2007.

[14]LEHMANN K. A framework for semantic invariant similarity measures for εLH concept descriptions[D].Dresden: Dresden University of Technology, 2012.

[15]LEHMANN K, TURHAN A. A framework for semantic-based similarity measures for εLH-concepts[C]∥CERRO L F, HERZIG A, MENGIN J. Logics in Artificial Intelligence. Heidelberg: Springer, 2012: 307-319.

【中文责编：庄晓琼英文责编：肖菁】

2015-10-05《华南师范大学学报(自然科学版)》网址：http://journal.scnu.edu.cn/n.

国家自然科学基金项目(61272066)；教育部新世纪优秀人才支持计划项目(NCET-12-0644)；广州市科技计划项目(2014J4100031)

蒋运承，教授，Email: ycjiang@scnu.edu.cn.

一种面向形式概念分析的语义相似度计算框架

蒋运承*， 李璞， Akram AFTAB

(华南师范大学计算机学院，广州 510631)

为了计算形式概念分析的形式概念或概念格的语义相似度，利用描述逻辑概念作为形式背景的特征属性对形式概念分析的形式背景进行语义扩展，即利用领域本体(描述逻辑知识库)提出了形式背景的一种语义表示方法．在此基础上，基于形式背景的语义表示，利用描述逻辑推理(即本体推理)给出了一种面向形式概念分析的形式概念或概念格语义相似度计算框架，并且证明了实例化该架构所得到的语义相似度计算方法满足对称性和等价不变性等基本性质．

形式概念分析； 语义相似度； 描述逻辑