资产增长效应与市场有效性——基于风险因素的实证分析

刘兰兰，姚树洁，2

(1.诺丁汉大学,英国 诺丁汉 NG7 2RD；2.重庆大学 经济与工商管理学院，重庆　400044)



资产增长效应与市场有效性
——基于风险因素的实证分析

刘兰兰1，姚树洁1，2

(1.诺丁汉大学,英国 诺丁汉 NG7 2RD；2.重庆大学 经济与工商管理学院，重庆400044)

以1998年至2015中国A股上市公司为研究对象，考察了Fama-French五因子模型对资产增长效应的解释能力。研究发现，投资增长风险因子对组合收益率的分布有显著影响，Fama-French五因子模型可以解释资产增长效应。除了市值规模因子和投资增长因子外，其他因子对股票横截面收益的预测能力并不显著。基于此，探讨影响资产价格变动的风险因子，并建立适当的资产定价模型，有利于改善中国股市的资源配置功能。

资产增长效应；投资组合；资产定价模型；风险因子

一、研究问题

股票收益率的可预测性是现代金融研究的核心问题之一。近年来，大量文献针对公司资产、投资规模的变化对未来股票收益率的影响展开了研究。理论研究方面，根据Tobin的Q投资理论，公司投资的目标是通过最优化的决策来实现股票市值的最大化[1]。基于此理论，Cochran证明，公司投资水平的变化反映了其未来贴现率或产出水平的变化，最优化的投资意味着投资期末所获得的边际效益的贴现值至少等于其投资期初的边际成本[2]。换言之，投资回报率应大于等于资本市场上的贴现率。实证研究方面，学者们主要针对公司资产负债表规模的变化与股票预期收益的相关性进行了探讨。例如，Cooper等发现了“资产增长效应”，即公司总资产的增长与股票预期收益呈负相关关系，资产扩张速度快的公司未来股票收益反而较低[3]。

目前，国内外学者对资产增长效应的存在性已基本达成共识。Watanabe等验证了该效应在42个国际股票市场中的存在性，并且发现基于该效应的多空套利策略可获得约6.4%的年化超额收益[4]。然而，学术界对于该现象的解释至今还存在争议。这些研究大致分为四个方面：(1)基于行为金融理论的错误定价解释；(2)基于Q投资理论的边际投资收益解释；(3)基于实物期权理论的风险因素解释；(4)以及基于有效市场理论的资产定价解释。此外，从针对中国A股市场上资产增长效应的研究看，黄迈和董志勇[5]、林祺[6]证明了公司资产增长对股票横截面收益的预测能力，并从Q理论、套利限制等角度来解释该效应，指出中国资本市场有效性不足。

本文主要考察了资产定价模型对于中国资产增长效应的解释能力。Fama指出，市场有效性的检验需要考量现有的资产定价模型是否是衡量股票收益风险的适当标准[7]。受理论及实证研究证据的启发，Fama和French[8]等提出的Fama-French五因子模型中，将投资增长率作为了新的风险因子。结果显示，改善后的定价模型对美国市场股票收益率的解释能力有所增强。本文尝试将Fama-French五因子模型应用于中国股票市场，从时间序列及横截面两个维度分析了该模型对于资产增长效应的解释能力，考察了投资增长因子的定价效果，为中国股票市场异象的检验提供了可借鉴的分析视角及实证证据。

二、文献综述

(一)国外市场有关资产增长效应的实证结果

资产增长效应最早是由Cooper等提出，证实了公司总资产规模的变化能够预测股票的未来收益。以1968年到2003年美国非金融类上市公司为样本，Cooper等发现总资产增长率最高的投资策略组合在接下来一年内的股票收益反而最低。他们的研究还探讨了基于资产增长效应的多空套利策略的盈利能力。具体而言，通过买入高资产增长公司的股票，并同时卖空低资产增长公司的股票，投资者所持有的等权重投资组合可产生约19.5%的年化超额收益。

为解释这一发现，Cooper等检验了资产增长效应是否源于公司资产负债表某一个或几个项目的变化，如现金、非现金资产、固定资产、设备或其他长期资产。实证结果表明，各项目的变化并不能很好地解释总资产增长率与预期收益之间的负相关关系。此外，总资产增长率对横截面收益的预测性要强于其他变量，如市值规模、账面市值比、股票动量等。同样地，Lipson等比较了七个衡量公司资产、投资水平变化的指标，证明总资产增长率可以有效地“吸收”其他指标对美国股票横截面收益的预测能力[9]。Yao等以1981-2007年9个亚太国家和地区上市公司为样本，发现了普遍资产增长效应，且在印度股票市场上最为显著[10]。

除了总资产增长率，大量文献从其他角度就公司资产、投资水平对股票收益的影响展开了研究，众多经济变量如资本支出率、净资产增长率、股本变动率等均被证明与股票预期收益呈负相关关系。例如，Xing以资本支出/账面价值比为衡量公司投资水平变化的指标，发现投资增长效应对股票收益的预测能力相较于价值效应更稳健[11]。

(二)资产增长效应的成因

1.错误定价

目前，在探讨资产增长效应成因的相关文献中，“错误定价”是受关注度最高的解释之一。这些文献主要从投资者行为偏差和有限套利理论的角度对资产增长效应进行了验证，并对市场有效性提出质疑。最早提出该效应的Cooper等发现，高资产增长的公司在扩张前几年内的经营业绩要明显好于扩张后的业绩。因此，投资者对公司过往业绩的“过度反应”使股票价格被高估，进而引发了错误定价。公司在大规模资产扩张后，股票收益率呈现为负值，这其实是市场对于其股价被高估的一种矫正。

第二个解释是有关管理者“过度投资”和投资者“反映不足”的假设。Titman等以超额资本支出为变量，从管理者建立“企业帝国”动因的角度，考察了对公司投资支出以及股票收益的影响[12]。该研究发现，在管理者拥有较高自由裁量权的公司以及敌意并购多发的时期内，超额资本支出与股票收益的负相关性更为显著。这说明投资者往往低估了管理者在公司扩张时期的意图，进而引发了错误定价。

Lam和Wei从第三种角度探讨了错误定价对资产增长效应的解释效果，即“有限套利”理论。该理论认为即使存在股价高估或低估的情况，由于信息不对称、交易成本的存在，使得理性投资者的套利行为不能够有效地将股价“纠正”回到合理的水平[13]。Lipson等以股票的特质波动率风险(Ivol)作为衡量有限套利的变量，发现套利策略所产生的超额收益仅存在于特质波动率风险高的样本，也就是套利成本较高的样本。

2.Q投资理论

Tobin指出，企业的投资行为由股票的市场价值与资产的重置价值之比，即Q值决定。当Q值大于1时，说明企业投入的资本量小于资本存量，这时企业可增加资本投入量，反之亦然。随后，Cochrane建立了一个基于Q投资理论的资产定价模型，证明贴现率与投资水平负相关。该模型的理论基础在于企业的边际Q值并不等于平均Q值，而是随投资边际成本(公司的资本成本，亦即投资者的期望收益率)的变化而变化。一般来说，当投资者的预期收益较低时，公司的资本成本越低，边际Q值越高，因而投资支出也就越高。

Li和Zhang指出，在无摩擦的资本市场条件下，不存在融资约束问题，各公司在资本市场上融资的成本基本相同。然而在现实的资本市场中，由于信息不对称的存在，不同公司的投资成本亦有所不同[14]。他们的理论模型显示，当公司的投资成本增加时，其投资的投入量对股票期望收益变化的弹性也就越大。基于此，Li和Zhang以1968年到2008年美国股市非金融行业上市公司为样本，检验了融资约束对投资—收益负向关系的影响。然而，实证结果与假设并不相符，说明该理论不能很好地解释资产增产效应。Yao等对亚太国家股票市场的研究发现，过度依赖银行融资以及金融系统的脆弱性是解释资产增长效应的最主要因素，这一结论与Q理论的论述相一致。

3.实物期权理论

与前文所论述的两种解释方式相比，基于实物期权理论的文献相对较少。Berk等提出，企业资产的价值是由现有资产以及可以行使投资机会的实物期权组成[15]。Carlson等将实物期权理论应用于公司投资行为的实证检验中，发现公司资产的系统性风险是随时间变化的。当公司执行实物期权并进行投资时，整个公司未来现金流以及资产价值的不确定性将有所降低，风险的降低将使公司的股票预期收益下降[16]。因此，他们证明实物期权理论可以用来解释公司投资增产和股票收益的负相关关系。

4.资产定价模型

根据资产定价模型的假设，投资者是厌恶风险的，因而收益与风险正相关。尽管大量文献证明，资产增长效应显著存在于规模小、特质波动率风险高、融资约束程度高的投资组合中，但是这些研究忽视了对于多空套利策略所产生的超额收益率的解释。

为了考察投资、盈利等非风险的变量与股票收益的相关性，Fama和French以股利贴现模型为理论基础，并结合相关的实证研究，提出了新的五因子模型。这一模型在Fama和French[17]所提出的三因子模型的基础上，增加了两个新的风险因子：盈利能力因子(RMW)以及投资增长因子(CMA)。Fama和French的结果表明，五因子模型对于个股收益率的差异、预期收益的横截面方差的解释能力均优于三因子模型以及CAPM模型。其中，投资增长因子代表股票的投资增长溢价，对于市值规模*投资增长交叉分组的25组投资组合的收益有很强的解释能力，且仅有1组的CMA回归系数显著异于零。此外，Hou等[18]也探讨了将三因子模型中的价值因子(HML)换成投资因子(I/A)和净资产回报率因子(ROE)的可行性，发现新的四因子模型对动量异象、投资异象以及盈利异象的解释能力要强于三因子模型以及卡哈特[19]四因子模型。

(三)中国股票市场资产增长效应的存在性及解释

尽管中国资本市场发展的历史较短，但是大量文献已经对资本市场的有效性开展了深入研究并取得了一定进展。资产增长效应作为广受国外金融文献关注的金融异象，已有国内学者就该效应在中国股票市场的存在性以及成因进行了验证。

叶建华和周铭山以2000年到2009年A股上市公司为样本，发现总资产增长率与股票横截面收益正相关，并显著存在于市值规模较大的样本中。该结论与美国等股票市场的研究结果相悖[20]。黄迈和董志勇则检验了1996年到2011年上市公司的收益率与资产、投资水平之间的相关性，发现总资产增长率、经股本变动率和投资增长率均对股票横截面收益有显著的负向影响[5]。赵胜民、闫红蕾、张凯[21]，以及周骆、张德礼[22]都应用了Fama-French五因子分析法对中国A股市场进行了实证研究，他们的研究结果证明这个实证方法是比较有效的。该研究还探讨了市值规模、资产负债率等衡量融资约束的变量对于资产增长效应的影响，结果证明融资约束在一定程度上可以解释中国股票市场上的资产增长效应。林祺通过对资产增长效应成因的检验，考察了中国资本市场的有效性。该研究以1996年到2011年上市公司为样本，发现中国股票市场的资产增长效应主要源于市场的信息不对称以及投资者非理性，而并非源于风险溢价。

三、研究设计

(一)样本选择

本文的初始研究样本为1998-2015年中国A股市场的所有上市公司。在此基础上，本文遵循以往文献中的筛选方法对样本进行了以下处理：(1)鉴于金融行业公司财务报表的差异性以及行业监管的特殊性，剔除了金融行业的上市公司；(2)为了保证财务信息披露的充分性，剔除了上市时间短于两年的数据；(3)为了消除异常值的影响，对除股票收益之外的连续变量变量进行了1%分位及99%分位的winsorize处理。在经过上述处理后，最终的年度观测值为23 460。本文实证研究所使用的数据包括上市公司年度财务数据以及股票月度交易数据，均来自于国泰安CSMAR数据库。

(二)变量描述

1.总资产增长率

总资产增长率体现了一个公司整体规模的变化情况。因此，本文采用该变量作为衡量公司资产、投资水平变化的核心变量。遵循Cooper等所采用的方法，公司i在每年t的总资产增长率可表示为：

(1)

其中，TA为资产负债表中的资产总计项目。

2.其他控制变量

本文所采用的控制变量包括：市值规模(MV)、账面市值比(BM)、盈利能力(OP)以及资本性支出(CAPX)。其中MV是指流通市值，即股票月收盘价与流通股数的乘积；BM为市净率的倒数，即公司在t年末所有者权益合计值除以当年12月的流通市值；OP为经营利润，即营业利润与所有者权益合计值之比；CAPX为公司在t年末的资本支出与上年总资产之比,其中，资本支出计算公式为：经营租赁所支付的现金+购建固定资产、无形资产和其他长期资产所支付的现金-处置固定资产、无形资产和其他长期资产而收回的现金净额。

(三)投资组合的构造

Black等最早采用投资组合(portfolio)的方法来检验CAPM模型对于股票横截面收益的解释能力[23]。与个股检验相比，投资组合分析在一定程度上消除了不同股票收益的异质性，因而降低了异常值的影响。

为了检验资产增长与投资组合收益率分布的关系，本文借鉴了Fama和French构造投资组合的方法。具体而言，每年t的6月底，我们将样本内的所有公司按照其上一财年末的总资产增长水平进行排名，然后依照排名的十分位将公司平均分为10组。本文研究中还考虑了将样本分为五组的情况并进行了检验，结果与十分组基本一致，故不在正文中列出。投资组合“1”包含的是资产增长最少的公司，而组合“10”则包含资产增长最高的公司。每个投资组合的持有期为12个月，从t年的7月初至t+1年的6月底，并在每年6月底依照新的财务数据重新构造投资组合。

依照Fama和French的方法，本文所使用的财务数据与股票收益率数据之间有6个月的间隔期，这主要是为了确保投资者在构造投资组合之前可以获得公司的财务信息。中国上市公司的会计年度采用日历年度制，一个财年是从每年的1月1日到12月31日。一般来说，中国上市公司的财务年度报告时间为每个财年结束的4个月左右。

除了10个投资组合的收益率之外，本文的研究重点在于检验公司资产增长所包含的信息是否给投资者提供了套利机会。通过构造一个多空套利策略组合(L-H)，即买入并持有低增长公司股票的同时，卖空高增长公司的股票，我们将检验该组合经风险调整后的收益率是否显著异于0。若该组合超额收益率为0且显著，则否定了资产增长效应的存在性。

(四)投资组合收益率的计算

在计算组合收益率时，本文采用了等权重加权(EW)和市值加权(VW)两种计算方法。具体来说，每个投资组合的月度收益率等于该组合内单只股票的月收益率与其对应权重乘积的加和。在12个月的持有期内，投资组合的收益率则等于每个月度收益率的平均值。

Liu和Strong指出，在计算“买入并持有”的投资组合收益率时，传统的方法假定每只股票的权重在持有期内保持不变(即1/12)[24]。然而，随着持有期内股票价格的变化，每只股票在每个月所产生的收益对于该组合的贡献也在变化，每个月带给投资者的财富并不相同。因此，传统的组合收益率计算方法并不符合实际情况，存在一定的偏差。依照Liu和Strong提出的持有期收益率分解法，本文在计算投资组合12个月持有期内的收益率时做了以下调整。

(2)

(3)

其中，投资组合在第1个月的收益率算法与传统方法一致，在第2-12月，将依照每只股票在持有期间对组合收益率的贡献对其权重wi进行调整。这一方法更真实地反映了投资者在持有一个投资组合时每个月财富的变化情况。

(五)研究模型

1.Fama-French五因子模型

近年来，大量国内学者考察了Fama-French三因子模型在中国股票市场的适应性，并普遍使用该模型来检验市场异象。研究发现，Fama-French三因子模型并不能很好地解释时间序列的资产增长投资组合收益率。基于此，本文采用了Fama-French五因子模型作为风险衡量的基准，回归模型如下：

(4)

其中，γp为投资组合P从1998年7月到2015年6月期间的月度收益率；γf为无风险利率，即月度化的一年定期储蓄利率；MKT为市场因子，即A股流通市值加权指数的月度收益率与无风险利率之差；SMB为市值规模因子；HML为价值因子；RMW为盈利能力因子；CMA为投资增长因子；β为时间序列回归后得出的各风险因子的系数；αFFS则是投资组合的超额收益率。

按照Fama和French的方法，本文采用2*3的交叉分组方式构造风险因子：首先，将A股市场上的所有股票按市值规模的中位数分为大规模(B)和小规模(S)两组；其次，以30百分位和70百分位为标准，将股票分为高价值(H)和低价值(L)、高盈利(R)和低盈利(W)、高增长(A)和低增长(C)；最后，按照市值*价值、市值*盈利、市值*投资增长进行交叉分组后，逐月计算市值加权的高/低组合收益率的差值，并将所得出的价差作为相应风险因子。

2.Fama-Macbeth横截面分析

为了进一步验证风险因子的显著性，本文采用了Fama和Macbeth[21]所提出的横截面回归方法对股票收益率的可预测性进行估计。具体而言，横截面回归分析分为以下两步。

第一步：每个月进行一次横截面回归，回归模型如下：

(5)

其中，被解释变量为样本中单只股票的月度收益率减去无风险利率，解释变量β为单只股票所在投资组合的风险因子的贝塔系数(公式4)。横截面分析所得出的回归系数γ则为5个风险因子的载荷。

第二步：将样本期内N个时间序列风险因子载荷进行平均，并使用t检验来考察其显著性，如：

(6)

四、实证分析

这一节就资产增长投资组合收益率的分布、时间序列回归、横截面回归的实证结果进行探讨。

(一)基本检验

本文首先考察了按总资产增长率分组的10个投资组合的公司基本面，结果如表1所示。

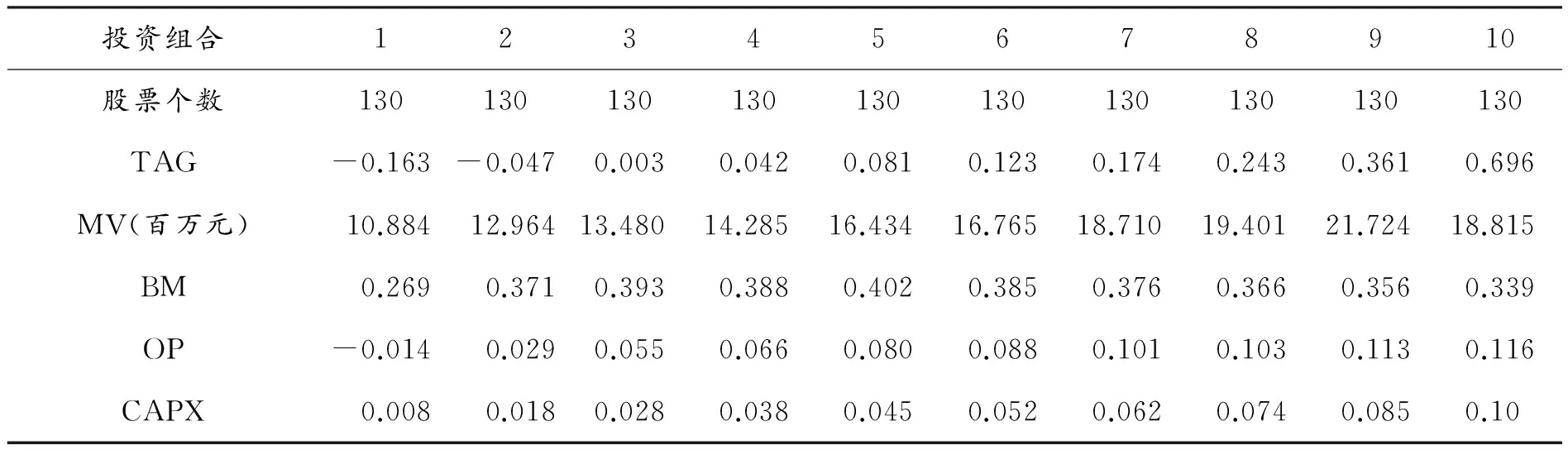
表1　资产增长投资组合基本特征

其中，表1中第一行列出了投资组合中所包含的股票数量，第二行至第六行列出了各组合公司的基本面情况，为每年度各变量中位数的平均值。具体看，资产增长投资组合在每个持有期内的股票个数约为130只。总资产增长率(TAG)从组合1到组合10单调递增，且增长趋势与美国市场数据保持一致。此外，资产增长低的公司为规模最小、账面价值最低、利润率最低以及资本支出最少的公司。相对而言，资产增长高的公司基本面相对良好，且规模较大、盈利能力强以及资本支出最多。然而，随着总资产增长率的上升，各投资组合的账面市值比变化趋势并不明显，意味着价值因子并不是衡量资产增长投资组合风险的适当标准。

(二)投资组合的收益率

表2报告了10个投资组合的收益率分布情况。其中A表提供了等权重加权收益率(EW)和分解后的等权重加权收益率(Decomposed EW)，B表提供了市值加权收益率(VW)和分解后的等权重加权收益率(Decomposed VW)。如A表所示，从资产增长最低的组合“1”到资产增长最高的组合“10”，等权重的月均收益率从2.078%单调递减至1.540%，呈现资产增长越高，收益率越低的趋势。同时，低增长和高增长套利组合的收益率之差(H-L)为0.539%，且在1%的水平上显著异于0(t=2.59)。这一数值约为Cooper等所报告的美股市场上的收益率数值(1.04%)的一半。此外，分解后的等权重投资组合的收益率有所降低，说明调整后的权重考虑了每个持有期内的调整成本。在使用市值加权法计算收益率时，H-L组合的收益率为0.431%，且显著程度有所下降(t=2.01)，这说明市值规模与资产增长投资组合收益率的分布存在一定相关性。

表2　资产增长投资组合毛收益率均值(百分比)

注：***和*分别表示检验值在1%、5%和10%的水平上显著；括号内为t统计量。

(三)时间序列回归

为了进一步验证中国股票市场是否存在资产增长效应，本文使用时间序列分析模型考察了风险调整后的组合收益率的表现。本节中所采用的收益率为分解后的等权重加权的收益率(Decomposed EW)。表3报告了使用CAPM、Fama-French三因子模型及五因子模型进行时间序列回归后得到的投资组合超额收益率α。从A表中可以看出，CAPM和Fama-French三因子回归所得到的套利组合(H-L)的超额收益率分别为0.483%、0.321%，且均在5%的水平上显著异于0。而在Fama-French五因子回归中，该套利组合的收益率在经济学意义上和统计意义上均不显著，这说明加入盈利因子或投资因子后的五因子模型能够很好地解释不同投资组合间的收益率差异。

表4列出了时间序列回归得到的风险因子系数及各模型的自由度调整系数。在CAPM回归中(表A)，10个资产增长投资组合的MKT系数均显著为正，且低增长公司对市场风险的敏感度要高于高增长公司。然而H-L套利组合MKT系数仅在10%的水平上显著，表明市场风险因子不能解释资产增长投资组合收益率的变化规律。在Fama-French三因子回归中(表B)，市值规模因子和价值因子对H-L套利组合收益率均有显著的解释作用。但是，10个资产增长投资组合的HML系数均为负值，主要是由于这些投资组合的平均账面市值比较小，价值因子对其收益率的解释能力有限。

在加入盈利因子和投资增长因子后(表C)，仅有投资增长因子可以解释H-L套利组合的收益率(βCMA=1.107，t=8.24)。此外，资产增长越小的投资组合，具有越大CMA系数，说明其高收益率与高资产增长风险溢价有关。从各模型修正后的R2看，Fama-French五因子模型对投资组合收益率的拟合度亦优于其他两个资产定价模型。

表3　风险调整后的资产增长投资组合超额收益率均值(百分比)

注：***和*分别表示检验值在1%、5%和10%的水平上显著；括号内为t统计量。

表4　资产定价模型风险因子系数

注：***和*分别表示检验值在1%、5%和10%的水平上显著；括号内为t统计量。

(四)横截面回归

本节采用Fama-Macbeth横截面分析方法,考察投资风险因子CMA对中国A股股票横截面收益的变动的解释作用。表5报告了Fama-French三因子和五因子的载荷，亦即因子的风险溢价。若资本增长因子CMA是影响资本资产价格变动的风险因子，那么其载荷应当为正值且显著异于0。

从A表可以看出，规模因子对股票横截面收益的预测能力要强于其他因子，投资增长因子的载荷为0.328，处于边缘显著水平(t=1.72)。由于中国股市样本中的股票数量是随时间递增的，因此在前端样本期的估计值标准差要大于后段。基于此，B表中列出了按每个月样本股票数量加权的因子载荷。在考虑了股票数量的变化后，规模因子和投资增长因子载荷的显著性有所增强，其他因子的解释能力几乎不存在。此外，表5的回归结果进一步确认了Fama-French五因子模型的解释能力比三因子模型有所提高。

表5　Fama-Macbeth横截面回归结果

五、结论与建议

本文研究了中国A股市场资产增长效应的存在性，重点考察了资产定价模型的解释作用。本文的实证结果表明：(1)在不考虑风险调整的前提下，中国A股市场存在资产增长效应，即公司资产增长与预期收益率呈负相关。(2)Fama-French五因子模型，尤其是投资增长风险，可以很好地解释资产增长投资组合股票收益率的差异。(3)规模因子和投资增长因子对中国A股横截面收益的预测能力在统计意义上显著，其他因子则不存在显著的预测能力。

本文的研究成果揭示了Fama-French五因子模型在中国股票市场的适用性，对于中国资产定价的适当方法的探索及市场效率的提高具有重要的借鉴意义。从实证研究的角度看，大量文献证明了中国股票市场存在异象，并对市场有效性提出了质疑。目前，对于影响中国资产价格变动的共同因子，学术界尚无定论。本文尝试应用了新的定价模型，并指出了中国股市存在规模风险和资产增长风险，为进一步探讨中国股票市场的有效性具有启示意义。从政策建议的角度看，中国股市资源配置功能的改善更需要对于股票定价因素的深入分析，找出适当的风险衡量方法。

[1]TOBIN J.A general equilibrium approach to monetary theory[J].Journal of Money Credit & Banking,1969,1(1):15-29.

[2]COCHRANE J H.Production-based asset pricing and the link between stock returns and economic fluctuations[J].Journal of Finance,1991,46(1):209-37.

[3]COOPER M J,GULEN H,SCHILL M J.Asset growth and the cross-section of stock returns[J].Journal of Finance,2008,63(4):1609-1651.

[4]WATANABE A,XU Y,YAO T,et al.The asset growth effect:Insights from international equity markets [J].Journal of Financial Economics,2013,108(2):529-563.

[5]黄迈,董志勇.Q理论、融资约束与资产增长异象[J].经济科学,2012(3):50-60.

[6]林祺.资本市场效率与资产增长异象——最优投资效应假说vs.错误定价假说[J].经济学(季刊),2016(2):767-796.

[7]FAMA E F.Efficient capital markets:II[J].Journal of Finance,1991,46(46):1575-617.

[8]FAMA E F,FRENCH K R.A five-factor asset pricing model[J].Journal of Financial Economics,2015,116(1):1-22.

[9]LIPSON M L,MORTAL S,SCHILL M J.On the scope and drivers of the asset growth effect[J].Journal of Financial & Quantitative Analysis,2009,46(6):1651-1682.

[10]YAO T,YU T,ZHANG T,et al.Asset growth and stock returns:Evidence from Asian financial markets[J].Pacific-Basin Finance Journal,2010,19(1):115-139.

[11]XING Y.Interpreting the value effect through the Q-theory:An empirical investigation[J].Review of Financial Studies,2008,21(4):1767-1795.

[12]TITMAN S,WEI K C J,XIE F.Capital investments and stock returns in Japan[J].Journal of Financial & Quantitative Analysis,2004,39(4):677-700.

[13]LAM F Y E C,WEI K C J.Limits-to-arbitrage,investment frictions,and the asset growth anomaly[J].Journal of Financial Economics,2011,102(1):127-149.

[14]LI D,ZHANG L.Does Q-theory with investment frictions explain anomalies in the cross section of returns?[J].Journal of Financial Economics,2010,98(2):297-314.

[15]BERK J B,GREEN R C,NAIK V.Optimal investment,growth options,and security returns[J].Nber Working Papers,1995,54(5):1553-1607.

[16]CARLSON M,FISHER A,GIAMMARINO R.Corporate investment and asset price dynamics:Implications for the cross-section of returns[J].Journal of Finance,2004,59(6):2577-2603.

[17]FAMA E F,FRENCH K R.Common risk factors in returns on stocks and bonds[J].Journal of Financial Economics,1993,33(1):3-56.

[18]HOU K,XUE C,ZHANG L.Digesting Anomalies:An investment approach[J].Social Science Electronic Publishing,2012,28(3).

[19]CARHART M M.On Persistence in mutual fund performance[J].Journal of Finance,1997,52(1):57-82.

[20]叶建华,周铭山.有限套利能否解释A股市场资产增长异象[J].南开管理评论,2013,16(1):41-48.

[21]赵胜民,闫红蕾,张凯.Fama-French五因子模型比三因子模型更胜一筹吗——来自中国A股市场的经验证据[J].南开经济研究,2016(2):41-59.

[22]周骆,张德礼.中国股票市场的有效性实证研究——基于Fama-French五因子模型[J].经营管理者,2016(2):16-16.

[23]JENSEN M C,BLACK F,SCHOLES M S.The capital asset pricing model:Some empirical tests[J].Social Science Electronic Publishing,1972,94(8):4229-4232.

[24]LIU W,STRONG N.Biases in decomposing holding-period portfolio returns[J].Review of Financial Studies,2008,21(5):2243-2274.

[25]FAMA E F,MACBETH J D.Risk,return,and equilibrium:Empirical tests[J].Journal of Political Economy,1973,81(3):607-636.

(责任编辑傅旭东)

Asset growth effect and market efficiency:An empirical analysis of risk factors

LIU Lanlan1,YAO Shujie1,2

(1.The University of Nottingham,Nottingham UK NG7 2RD; 2.School of Economics and Business Administration,Chongqing University,Chongqing 400044,P.R.China)

Using the sample of Chinese listed A-shares from 1998 to 2015,this article investigates the explanatory power of Fama-French five factor model in explaining the asset growth effect.Empirical results show that the model has strong power in explaining the effect,and the investment risk factor is priced.Among the five factors,only the size factor and the investment factor are predictive for forecasting A-share’s cross-sectional stock returns.Based on these findings,we find the investigation of risk factors and appropriate asset pricing models are vital for improving the resource allocation function of Chinese Stock Market.

asset growth effect; efficient market; asset pricing model; risk factors

10.11835/j.issn.1008-5831.2016.05.004

欢迎按以下格式引用：刘兰兰，姚树洁.资产增长效应与市场有效性——基于风险因素的实证分析[J].重庆大学学报(社会科学版),2016(5):34-42.

Format:LIU Lanlan,YAO Shujie.Asset growth effect and market efficiency:An empirical analysis of risk factors[J].Journal of Chongqing University:Social Science Edition,2016(5):35-42.

2016-09-05

刘兰兰，英国诺丁汉大学金融与风险专业博士(全额奖学金)，主要从事资产定价、证券投资策略及金融市场微结构分析研究,E-mail:164302749@qq.com。

姚树洁(1960-)，男，广东人，重庆大学经济与工商管理学院教授，重庆市首席专家(经济学)，长江学者特聘教授，复旦大学和西安交通大学特聘讲座教授，诺丁汉大学当代中国学学院创建院长,经济学教授，全英中国专业团体联和会副主席,联合国开发计划署和世界银行经济顾问，著名华裔经济学家，主要从事经济发展、贫困缩减等研究。

F830.91

A

1008-5831(2016)05-0034-09