浅析高中数学课堂的有效构建

周　华

(江苏省启东市吕四中学，226241)



浅析高中数学课堂的有效构建

周华

(江苏省启东市吕四中学，226241)

自新课标实施以来,很多学校的教师都对高中数学课堂有效构建进行了有益的探索.但是，不容否认的是,当前不少课堂仍然处于低效甚至无效状态.怎样构建有效课堂?笔者认为,最根本的原因还在于课堂教学中以学生为本的理念没有得到有效体现．这里，笔者结合自己的教学实践,在尊重学生主体地位的基础上,重点就高中数学课堂有效构建的具体策略进行探讨,供参考．

一、从激发兴趣出发创设情境

课堂导入,时间虽短,但是却能直接影响课堂教学的效果．所以，教师需要重视课堂导入,尽可能创设情境,搭建平台,激发学生内心参与欲望,从而有效提升课堂效率．但是，不少老师从高考角度和高中学生年龄实际考虑,认为学生自学能力强,因而对于课堂导入不够重视,往往开门见山,直奔主题，这种观点是片面的．

案例1针对等差数列的求和公式这一内容,笔者没有按照常规,而是从有关高斯小时候的数学故事入手.对“1+2+3+…+100=？”这一道题,高斯几分钟就能算完，“你们算算看,这道题的结果是多少?”这里，笔者“故弄玄虚”．学生很快回答:“5 050!”“是的,你们都熟悉,具体算法很简单,即101×50=5 050．”于是笔者话锋一转,接着说:“你们看着很简单,但是对于七八岁的小学生不简单,因为这里运用了等差数列求和理念．现在我们就来推导公式,尝试用理论来解决问题,你们来试试,与高斯比一比,怎样?”学生思维被激活,自然热情高涨,参与欲望强烈.这时，教师可以适时给学生安排下面的练习:

(1)前n个奇数的和:1+3+5+…+(2n-1)=______;

(2)前n个偶数的和:2+4+6+…+2n=______.

借助这两道题,让学生从高斯故事中借鉴方法,从而寻找其中数学方法以及其中蕴含规律,从而有效激发学生求知欲望,为学生进一步学习和教学活动的有效开展提供了有利条件．

二、从个性实用出发夯实目标

对于课堂教学目标,很多老师往往结合课标,追求大而全,造成这样的教学目标,看似正确,但是要求模糊,而且之间跨度大,很难在一节课中能够让学生做到．所以,要真正制定出符合课堂实际的个性目标,教师就必须吃透教材,尤其是对概念的内涵与外延更需要有深入的了解.当然，作为课堂主体学生更需要重点关注,才能真正制定出符合课堂教学实际需要的目标．

解析对于本题,可以从临界法与第二定义入手．临界法比较常用,而第二定义则可以作为一种补充给学生拓展,而这需要学生能够对第二定义有所了解．这里,临界法可以作为基础目标,要求所有学生都能掌握,而第二定义则可以作为提升目标,要求学有余力的学生能够掌握．

解法1(临界法)

取M,A(右顶点)两点重合时的情况:

由题意MF1=2AA′，得

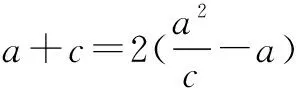
注意临界法出现多解现象需要注意逐一验证．

解法2(第二定义)

由椭圆第二定义，得MF1=e·MM1.

又由题意得MF1=2MM2，

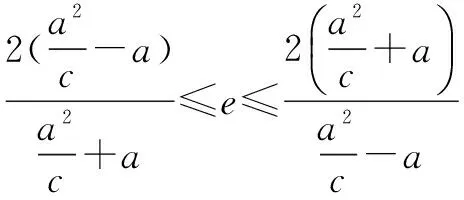
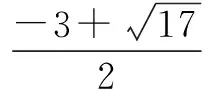
对于有效课堂来说,前提是能够让所有学生都能掌握基础性目标,然后才能推促部分学有余力的学生通过努力，达到提升性目标．

三、从课堂实践出发优化模式

对于高中数学来说,其教学过程具有高度抽象性与概括性,因而课堂有效模式需要教师主动践行,并具有一定的创造性,其实践过程必须有具体操作性．不同的课堂必须有不同的教学模式,下面笔者结合实践重点介绍几种模式:

1.情境体验模式

很多教师认为,高中学生已经不需要兴趣激发,其实这是一种误导．学生的自主性以及内在能动性,能够有效提高课堂效率．教师要在课堂上尽可能关注学生情感因素,通过改善活动过程给学生提供平台,创设情境,并能形成呼应．这种模式一般分为“情境——活动——体验”三个环节．

2.过程体验模式

对于这种模式来说,强调学生主体地位,强调学生的参与意识,主要是在教学过程中构建具有实践性和具有教育意义的活动．其基本特征是小组合作学习模式．

3.探究体验模式

对于高中教学来说,主要有两种模式,一种是学生被动接受,一种是主动探究．虽然它们之间各有千秋,但是不容否认的是探究体验教学模式更能符合当前教学趋势．这种教学模式,主要是以学生对知识的重组以及运用为着力点,采用学生自主探究的形式,着重培养学生创新精神,以适应社会发展需要．这种模式一般在概念以及定理规律等复习教学中运用．

4.互动体验模式

课堂互动是当前课堂教学一个重要环节.其教学模式一般主要是激励学生自主参与,继而通过学生之间多元互动,引发学生结合自主、合作、探究等学习方式实现共同提高．这里教师需要在课堂上强化指点,能够与学生多元互动实现有机渗透,从而推促学生对数学内容的理解,学生在与他人交流过程中不断完善自己的认识,加深对文本内容的理解.这样的模式在教学中既能发挥集体作用,又能彰显个性特征,从而有效提高课堂效率．

四、从良好习惯出发关注细节

细节决定成败．良好的学习习惯对于学生终身学习来说,具有非常重要的意义．要培养学生在课堂上养成良好习惯,前提是引导学生关注其学习细节．比如，当学生完成一个题目证明后,应当就解题过程中的困惑,以及收获进行反思．这种习惯的培养往往很多时候比学生掌握一个概念更为重要，教师要在课堂教学中注意引导．

案例3如图2，在四棱锥P-ABCD中,AB⊥AD,CD⊥AD,PA⊥面ABCD,PA=AD=CD=2AB=2,M为PC中点,BM∥面PAD,在∆PAD内找一点N,使MN⊥面PBD.

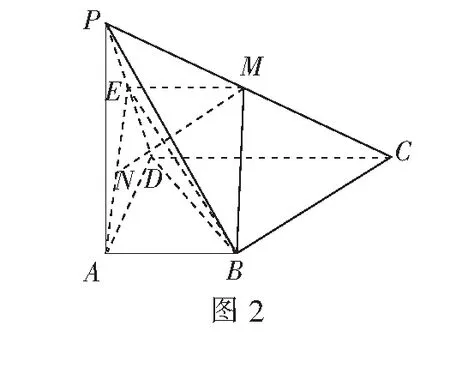
分析对于空间几何证明题来说,很多学生都会想到作辅助线,采用常规做法,由直线或者平面垂直的方式进行判断．其实在教学中采用空间向量知识点来解决,更为简单形象．可以在给出的垂直和边具体长度等已知条件入手,建立空间直角坐标系,写出坐标,这样整个解题过程就会非常清晰．容易想到只要取PD中点E,连结AE,再取AE中点N,以下证明MN⊥面PBD.

证明点A为原点，以DA为x轴,AB为y轴,AP为z轴建立空间直角坐标系，则

A(0,0,0)，P(0,0,2)，B(0,1,0)，

C(-2,2,0)，D(-2,0,0)，

M(-1,1,1)，E(-1,0,1)，

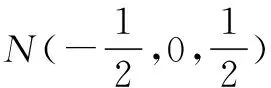
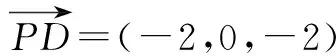
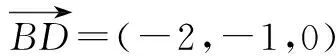
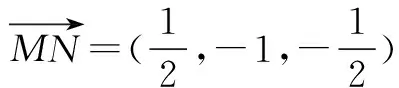
于是有

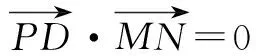
又PD交BD于点D,PD、BD⊂面PBD，

所以MN⊥面PBD.

对于解题过程来说,思路比方法更为重要．教师在教学中要引导学生进行思维发散,而这需要让学生能够从学习细节入手,并且把关注这些细节成为一种解题习惯,而这恰恰也是课堂有效举措之一．

总而言之,针对高中数学有效课堂构建,一方面需要结合学科特征,在吃透目标以及教本内容的基础上进行设计;另一方面也需要充分考虑学生主体地位,能够根据学生接受能力进行设计．当然，在课堂教学中,有效构建的策略还有很多,不过无论何种策略,关键一点就是,必须着眼于学生的终身发展,这是根本．