Hydrodynamic interactions of water waves with a group of independently oscillating truncated circular cylinders

Xiaohui Zeng·Min Shi·Shanlin Huang



RESEARCH PAPER

Hydrodynamic interactions of water waves with a group of independently oscillating truncated circular cylinders

Xiaohui Zeng1·Min Shi1·Shanlin Huang1

In thisstudy，we examine the waterwave radiation by arrays of truncated circular cylinders.Each cylinder can oscillate independently in any rigid oscillation mode with a prescribed amplitude，including translational and rotational modes such as surge，sway，heave，pitch，roll，and their combinations.Based on the eigenfunction expansion and Graf’s addition theorem for Bessel functions，we developed an analytical method that includes the effects of evanescent modes in order to analyze such arrays of cylinders.To investigate the effects of several influential factors on convergence，our objective is to dramatically reduce the number of tests required and determine the influencing relationshipsbetween truncation number and convergence behavior for different factor combinations.We use the orthogonal test method to fulfill the objective.Lastly，we present our results regarding the effects of evanescent modes on hydrodynamic coefficients.

Radiation·Water wave·Arrays of truncated circular cylinders oscillating independently·Translational oscillation·Rotational oscillation

1　Introduction

In recent years，various offshore floating structures designed for the exploitation of space and ocean resources have drawn increasing attention.These structures mainly comprise a sin-gle circular cylinder or an array of circular cylinders，such as deep-sea platforms，floating bases for wind power devices，or wave power extraction devices with oscillating cylinders［1-6］.

✉ Xiaohui Zeng

zxh@imech.ac.cn

1Key Laboratory for Mechanics in Fluid Solid Coupling Systems，Institute of Mechanics，Chinese Academy of Sciences，Beijing 100190，China

Many studies have focused on the hydrodynamic interactions between cylinders in waves，using numerical and analyticalmethods.Forexample，Wang etal.［7］investigated radiation by a group ofcylindersusing a finite-element-based numerical method.Zhou et al.［8］investigated the nonlinear radiated waves generated by a floating structure in forced motion by using a higher-order boundary element method（HOBEM）.Babarit［9］investigated the energy absorption problem in both regular and irregular waves，and considered wave interactions in arrays of two surging or heaving cylinders，whose hydrodynamic coefficientswere calculated using the boundary element method（BEM）.In addition，Williams et al.［10，11］used a modified plane-wave approach to investigate the diffraction and radiation problems associated with an array of truncated circular cylinders.Furthermore，Kagemoto and Yue［12］presented an accurate algebraic method（including the interactions of evanescent waves）for multiple bodies by combining and extending the matrix method and the multiple-scattering concept，based on the diffraction characteristics of the isolated member.Also，Linton and Evans［13］developed an exact theory for wave diffraction by vertical circular cylinders and achieved a major simplification.Additionally，Yilmaz［14］obtained analytical solutions for the wave scattering and radiation of truncated cylinders using the accurate algebraic method developed by Kagemoto and Yue［12］.Moreover，Siddorn and Eatock Taylor［15］also used an exact algebraic method to study radiation and diffraction in an array of cylinders oscillating independently.Then，Chatjigeorgiou［16］investigated wave diffraction by arrays of truncated elliptical cylin-ders subjected to regular waves and presented an analytical solution.and Guillot［22］examined the feasibility ofan intelligentsensor fusion to estimate on-line surface finish and dimensional deviations with the orthogonal arrays used for experiments planning.In addition，Green et al.［23］applied orthogonal arrays to conjoint analysis in marketing.Also，Lee et al.［24］used an iterative optimization algorithmwith orthogonal arrays in discrete space for structure design.The feasibility of a method that combines orthogonal experiment theory with the finite element method（FEM）was discussed by Wang et al.［25］，who used this method to compute and evaluate the three dimensional（3-D）natural stress field.In view of the high efficiency of orthogonal design in reducing the number of required tests or computations，we use this method in this study to investigate the effect of different influentialfactors（e.g.，oscillation mode and waterdepth）on convergence behaviors and to identify primary and secondary factors.Using the orthogonal test method，with a relatively small amount of calculation，we can identify how the numberofitemsretained in the expansion affects the convergence behavior in circumstances with different parameter combinations.Accordingly，we can then develop more reasonable calculation procedures for other cases.

In this study，we classify arrays of floating cylinders into two categories.The first is an“array of cylinders with no relative motion”（hereafter referred to as the“C1 array”）because the connection between the cylinders is so strong that the cylinders can be regarded as being rigidly connected as a whole.The second array category is an“array of cylinders with relative motions”（hereafter referred to as the“C2 array”）because there isno rigid connection between the component members and each component member can oscillate independently.
Studies of the hydrodynamic interactions between cylinders have mainly focused on the“C1 array，”and there are relatively few studies of the“C2 array”（especially using analytical methods）.Published results for the“C2 array”are mainly concerned with concrete examples in which each cylinder oscillates in translational modes（i.e.，surge，sway，heave）rather than there being an array of cylinders oscillating independently in rotational modes（i.e.，roll or pitch），let alone in multiple modes that include both translation and rotation.Asmore and more“C2 array”characteristicsemerge in new offshore structures，further investigation is merited regarding the hydrodynamic interactions of“C2 array”oscillations with multiple modes，including both translation and rotation.Therefore，in this study，we investigate water wave radiation and diffraction by the“C2 array”in the context of linear wave theory.
With respect to computation，the infinite series in equations must be truncated，so it is important to determine the appropriate number of terms retained in the expansion after truncation with lessthan about1%error.An isolated cylinder does not require much computation to obtain the appropriate truncation number by trial and error.However，it would be onerous and time consuming to do so for an array of cylinders，because the hydrodynamic problems are much more complex and there are more factors influencing convergence behavior.For the same reasons，it is very hard to obtain explicit mathematical expressions to analyze convergence behavior.If convergence were to be examined by trial and error for cases involving different factors，the costs would be prohibitive.Therefore，another alternative must be sought to determine the relationships between different influential factors and convergence behaviors.In this study，we adopted the orthogonal test method to determine these relationships.
The orthogonal test（experimental design）method is an efficient testing strategy for identifying the relationships between influential factors and the test index，as well as for differentiating the primary from the secondary factors in fewer trials.Since the 1940s，this method has been adopted by industry and academia［17-21］，and has found worldwide applications.There are many examplesofthe successful application of the orthogonal design.For example，Azouzi

2　Solutions for velocity potentials

Due to the axial symmetry of a circular cylinder，the yaw motion introduces no hydrodynamic forces in a perfect fluid. Therefore，only five modes-surge，sway，heave，roll，and pitch-are considered in this study.

The radius and draught of an isolated truncated cylinder are a and h，respectively，and the water depth is d.The fluid is divided into two regions（core and exterior），as depicted in Fig.1.

Figure 2 shows the six oscillation modes of a single truncated circular cylinder.

The array（Fig.3）consists of N verticaltruncated circular cylinders.We employ a right-handed Cartesian space fixed coordinate system XOY with the plane xoy coinciding with the still-water level（SWL），and the positive z-axis pointing vertically upwards.The coordinate of the origin Oiof each cylinderin the overallcoordinate system is（xi，yi）.The radius of each cylinder is ai，i=1，2，...，N.The local cylin-drical coordinate system Oiriθiz is centered on the origin of each cylinder.The coordinate of the origin Ojof cylinder j in the cylindrical coordinate system centered on the origin Oiof cylinder i is（Lij，αij，z），i，j=1，2，...，N.

Fig.1 Sketch of a single truncated circular cylinder

Fig.2 Array of truncated cylinders and six oscillation modes

Fig.3 Local cylindrical coordinate system for an array of truncated circular cylinders

Assuming that the fluid is inviscid and incompressible and that the flow is irrotational，we can employ the potential theory.We can consider the linear steady-state oscillations since the wave steepness and amplitudes of motion are small enough.Therefore，physical quantities such as the velocity potentials and displacements are periodic functions of time with angular frequency ω0.Then，the total velocity potential can be written as the product of the space and time factors，as follows

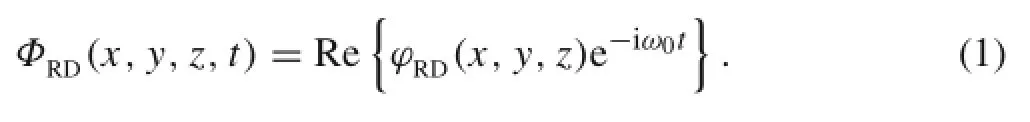
The potential ϕRDfor an array of cylinders with independent prescribed motions is the sum of the radiation and scattering potentials，which can be written as

The velocity potential in a linear water wave problem can be decomposed into the incident potential（due to environmental waves or other sources，such as waves emanating from other cylinders due to wave diffraction or radiation），diffraction potential（fixed cylinder but an incident wave），and radiation potential（oscillating cylinder without incident wave）.For the problem considered in this study，is the diffraction potentialofcylinder j；isthe radiation potential of cylinder j；with-the sum ofthe potentialofwaves emanating from othercylinders（i=1，2，...，N，except cylinder j）due to wave diffraction and radiation-acting as the incident potential on cylinder j.

The instantaneous displacement of cylinder i in smallamplitude periodic oscillation with angular frequency ω0is

where ζ（i）srepresents the oscillation amplitude of mode s for cylinder i.The corresponding velocity is

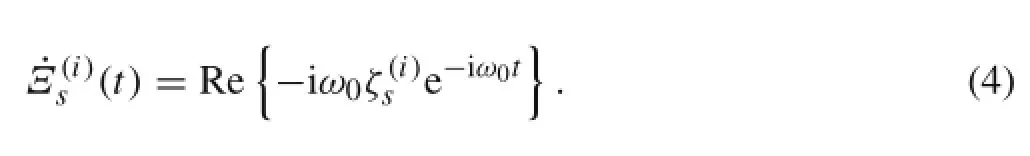
When cylinder i oscillates independently with amplitude ζ（i）sin mode s，the corresponding radiation potential is

According to the impermeable condition on the body surface，the normal velocity of the cylinder is equal to that ofthe adjacent fluid，and the equation is written as

Suppose the coordinate of the centroid of the cylinder isAs shown in Fig.1，the fluid domain is divided into two regions:the core region and exteriorregion.The radiation potentialsfor the exterior region and thefor the core region satisfy the impermeability conditions on the body surface，as follows

Apart from the body surface conditions，the velocity potentials for the exterior and core regions must satisfy Laplace’s equation，the free-surface condition，the seabed condition，and the radiation condition atinfinity，respectively，as follows

where Hm=Jm+iYmis an m-th-order Hankel function of the first kind.Jmand Ymare m-th-order Bessel functions of the first and the second kinds，respectively.Kmis a modified Bessel function of the second kind.

The wave number k0and the angular frequency ω0satisfy the usual dispersion relation

The eigenvalues kn（n=1，2，…）are the positive real roots of the following equations

In Eq.（10），Z0（z）and Zn（z）are expressed asin Eq.（13）can be solved using Eq.（A1）in the appendix

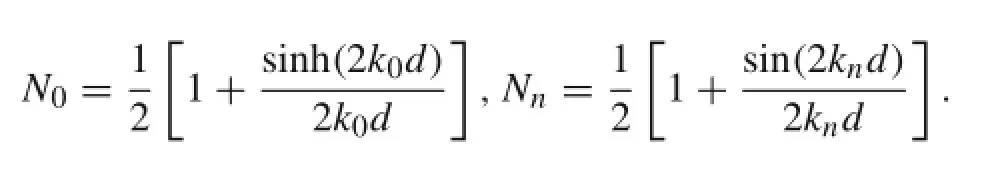
Equation（10）can be expressed in matrix form as

where“D-E”is short for“diffraction-exterior region”andrepresents the column vector of the partial radiation waves in the exterior region of cylinder i（except for the amplitude，the function form ofradiation and diffraction partial waves are the same in the exterior region，so we adopt the notationfor both radiation and diffraction partial waves in this paper）.

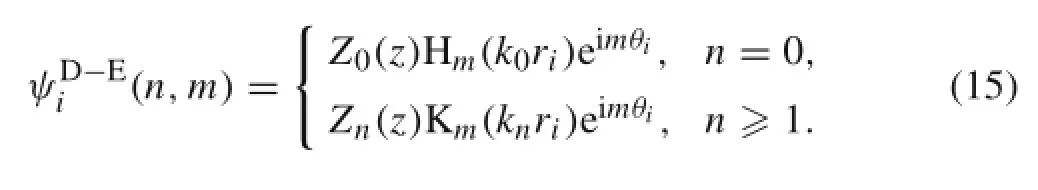
Using Graf’s addition theorem for the Bessel functions（valid for rj＜Rij）and replacing l by-l，Eq.（15）is rewritten as

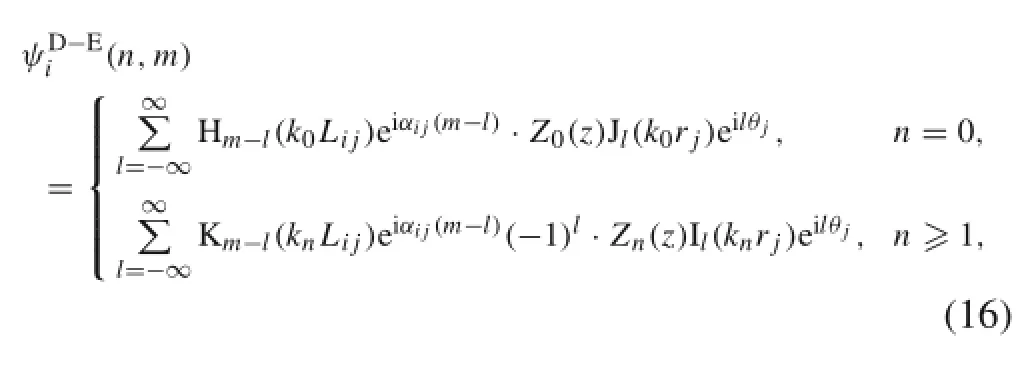
where Ilis the l-th-ordermodified Besselfunction ofthe first kind and Eq.（16）can be expressed in matrix form as

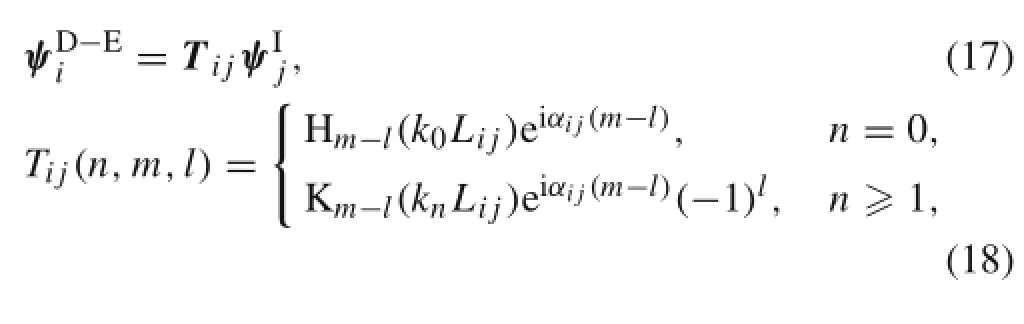
ψIjis an n0（2l0+1）column vector representing incident partial-wave functions written as

The diffraction potentialofthe exteriorregion in the vicinity of cylinder i，which is generated from radiation waves emanating from other cylinders，is

and its matrix form is

where ARiis an unknown column vector of n0（2m0+1） elements，and each element is，representing the amplitudes of the partial diffraction waves in the exterior region caused by cylinder oscillations.

The total incident potential in the vicinity of cylinder j is the sum ofthe radiation potentials caused by the independent oscillation ofother N-1 cylinders and the diffraction potentials due to the hydrodynamic interactionsbetween cylinders，as follows

For cylinder j，the diffraction potential（Eq.（21））and the totalincidentpotentialϕIj（Eq.（22））can be connected by the diffraction transfer matrixin the exterior region as

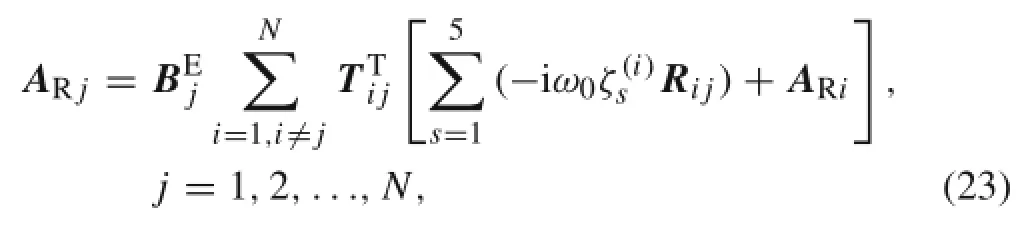
Given the prescribed amplitudeand the knownand Risvalues，the unknown vector ARj（n，m）can be solved from Eq.（23）.

Thus，the total exterior potential in the vicinity of cylinder j as each cylinder oscillates in different modes（s= 1，2，3，4，5）is obtained as

The total core potential of cylinder j is

C0mand Cnmin Eq.（26）are obtained from Eq.（A1）in the appendix.in Eq.（25）is the column vector of the partial-wave functions in the core regionin Eq. （25） is the diffraction transfer matrix for cylinder j in its core region， representing the amplitudes of the partial diffraction waves caused by unit-amplitude partial incident waves，which can also be found in the appendix.

Therefore，we obtain the velocity potential adjacent to cylinder j as each cylinder simultaneously oscillates with independent amplitudeIn Eq.（24），is the velocity potential for the exterior region in the vicinity of cylinder j.In Eq.（25），is the velocity potential for the core region of cylinder j.

3　Hydrodynamic forces and moments

Then，we can obtain the horizontal hydrodynamic forceson cylinder j as each cylinder oscillates in different modes

The verticalhydrodynamic forceon cylinder j is

where Sbis the side surface of a cylinder，with unit normal vector written as=（-cosθj，-sinθj，0）；Sbhis the bottom surface，with unit normal vector=（0，0，1）.

4　Comparisons and verifications

Fig.4 1-4 heave-heave and heave-surge.a Real parts.b Imaginary parts

Fig.5 Comparisons of hydrodynamic coefficients in pitch mode between present study and that of Ali and Khalil［26］.a Added mass.b Damping coefficients

Based on the method developed in the preceding sections，we wrote a computer program and then verified the program priorto performing furthercalculationsforthe hydrodynamic interactions between truncated circular cylinders in an array with some oscillating cylinders.

Note that Siddorn and Eatock Taylor［15］provided an example of the hydrodynamic interactions of an array of cylinders caused by one cylinder oscillating in translational mode with a prescribed amplitude.We then compared the results of our study with those of Siddorn and Eatock Taylor（Fig.14 in Ref.［15］），as shown in Fig.4a and b，in which the circularand square points denote the results of Siddorn and Eatock Taylor［15］，and the solid and dashed-dotted lines denote the results of our study.Using the nomenclature adopted by Siddorn and Eatock Taylor［15］，i-j designates interactions between cylinders i and j.Forexample，the label 1-4 heave-surge refers to the heave force on cylinder 1 due to unit surge velocity of cylinder 4.We observe good agreement，as the results of our study and Ref.［15］are almost identical，with maximum differences of 0.2%.

We also compared the results from this study with those from previous studies using the numerical method（3-D source-sink method）from Ali and Khalil［26］.For the cases shown in Fig.5a and b，the square and triangular points denote the results of Ali and Khalil［26］and the solid lines denote the results of this study.Comparisons of the results of this study with those of Ali and Khalil（Fig.14 in Ref.［26］）are shown in Fig.5a and b，respectively.For the cases shown in Fig.5a and b，there are three cylinders，andrefers to the pitch moment on cylinder 2 due to the unit pitch velocity of cylinder 1.We can see that the variation trends of the present and reference studies are identical，with the majority of differences in the results ranging from 0.2%to 9.9%.The numerical 3-D source-sink method was adopted in Ref.［26］and the accuracy of their results is dependent on many factors（such as the mesh discretization）.The results of our study agree well with those of Ref.［26］.

5　Investigations of truncation number using orthogonal test method

For an array of truncated cylinders，there are many factors that can affect convergence behavior，such as column number，column spacing，oscillation mode，water depth，draught，and wave number，and the appropriate truncated number（corresponding to convergent results）for different factorcombinations also differs.Itis very difficultto obtain explicit mathematical expressions suitable for an analysis of convergence.The trial-and-error examination of convergence for cases with different factor combinations would involve prohibitive costs.Therefore，we introduce the orthogonal test method in this study，which investigates（with a minimum number of tests）the relationships of influence between different influential factors and convergence behaviors，and identifies the primary and secondary factors.In this section，we present concrete examples for an array consisting of four cylinders placed at the vertices of a square.

For this study，we use the mixed-level orthogonal array L50（510×101），where L denotes a Latin square，50 is the numberoflevelcombinations，510indicates thatthere are ten factors and five levels per factor，and 101indicates that there is one factor that has ten levels.

After carrying out the tests according to the orthogonal array，we analyzed the data using a direct analytical method known as range analysis.The range（generally denoted by R）is the maximum average numerical difference of each factorateach level.Because the factors have differentlevels，a conversion coefficient is needed（generally denoted by d）. Then the formula of the revised range（denoted by R´A）is，where rAisthe frequency ofoccurrence of factor A in one column according to each level.Thus the primary and secondary factors can be analyzed by comparing the sizes of R´A.Table 1 shows the conversion coefficient d for different levels.

The influence of differentfactors（oscillation mode，water depth，draught，column spacing，and wave number）and theircombinationson convergence mustbe comprehensively investigated.In the array，the wave numberhas ten levels and other factors have five，respectively.Table 2 shows the factors，which are dimensionless，as well as their levels.

Once the factorsand theirlevels in the corresponding position are filled in the orthogonal array，then the calculation is carried outaccording to the orthogonalarray（here，we selectcolumns 1，2，4，7，and 11 in the orthogonal array）.We note that to investigate the convergence of the results，we compare the results solved from smallertruncation items（m=6，n=25，p=25）with those from large enough truncation items（m=6，n=60，p=60）.Before introducing the orthogonal test method to determine the appropriate truncated number，we performed many calculations by trial and error，and the resultsshow thatthere is almostno difference if the value of m is greaterthan 6.The maximum errorbetween m=6 and m=7 is about 0.0002%in the region of interest，so 6 is a sufficient value for m.The orthogonal array and calculation results are listed in Table 3.With the same truncation items，cases with large percentage errors require moretruncation items to achieve the same convergence accuracy，which means a slower convergence rate.

Table 1 Conversion coefficients

Table 2 Factors and their levels

Table 3 Orthogonal array and calculation results

Table 3 continued

Fig.6 Index fluctuation when k0a changes

We drew the following diagrams after processing the data in Table 3，since it is easier to observe from a diagram the index fluctuation when each factor’s level changes.

Figures 6-10 illustrate the mean error of each factor over the range ofcorresponding levels，respectively.Taking Fig.6 as an example，itwas drawn by calculating the mean value of the results（percentage error）at each level in the k0a column of Table 3.The above figures show that the convergence rate of a case with smaller wave numbers is significantly faster than that with larger wave numbers；the convergence rate ofthe case in surge or sway mode is faster than those in heave and rotational modes；the convergence rate of a case with a column spacing of 15a is much faster than cases with other column spacings in the defined range；the convergence rate increases significantly by increasing the draught-to-waterdepth ratio.

Fig.7 Index fluctuation when a ii changes

Fig.8 Index fluctuation when L/a changes

Fig.9 Index fluctuation when d/a changes

Fig.10 Index fluctuation when h/d changes

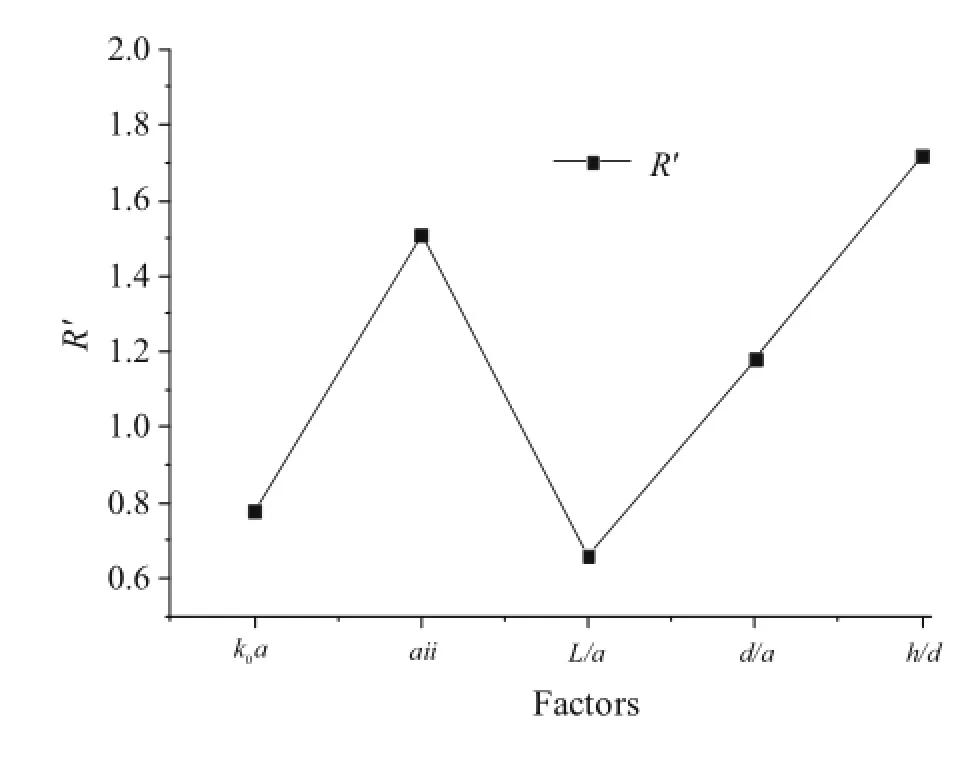
Fig.11 Primary and secondary factors

The range R of each factor can be obtained by processing the data in Figs.6-10，which helps to further analyze the primary and secondary factors.Since the wave-number level differsfromthatoftheothers，wecalculatedtherevisedrange R´to compare each factor’s effect on the index.

Figure 11 indicates that both the oscillation mode and the ratio of the draught to water depth have greater influence on the convergence rate than wave number and column spacing do.

Next，we designed a test case in which four cylinders are located at the vertexes of a square，with column spacing 5a，and water depth 20a，to verify the rule given above.First，we investigated the surge and pitch modes for a ratio of draught to water depth of 0.1，and then for the surge mode for ratios of 0.1 and 0.6.

WecanobservefromFig.12a-cthattheoscillationmodes andthedraught-to-water-depthratiohavearemarkableinfluence on the convergence rate；the convergence rate of the surge mode is faster than the pitch mode；the convergence rates of cases in which the draught-to-water-depth ratio is 0.6 are faster than those with the ratio 0.1.

Thus far，there is no effective way to properly estimate the truncated indices apart from trial and error.The above rule simplifies the investigation of convergence in the cases discussedbelow.Basedontheconclusionsdrawninthissection，cases with rotational modes or smaller ratios of draught to water depth should be given priority when investigating truncated features.If the value of some truncated items in the above cases satisfies the precision requirement，then the same value will satisfy cases with higher convergence rates，such as those with translational modes or larger ratios of the draught to water depth.As such，there is no need to perform trials for every case with different parameter combinations，which improves efficiency and saves a lot of time.

6　Results for several cases and discussion

6.1Hydrodynamic coefficients:the effects of evanescent modes

As mentioned above，there are some solutions available for arrays of circular cylinders that use large-spacing approximation，neglecting the evanescent modes in the velocity potential of emanating waves.In this study，the solutions include evanescent modes.Therefore，the effects of evanescent modes on the hydrodynamic interactions can be evaluated.In this subsection，we use two different algorithms to calculate the hydrodynamic forces of an array of cylinders: one includes evanescent modes and the other does not.Then we demonstrate the effects of evanescent modes by comparing the two sets of results.

6.1.1Two cylinders

First，we recalculated the hydrodynamic coefficients for two cylinders（case 1 in Williams and Abul-Azm［11］，where cylinder 1 oscillates and cylinder 2 is fixed）.Then，we compared the two sets of results（including and without evanescent modes）with that using a modified plane-wave techniquebasedonalarge-spacingapproximation（Williams and Abul-Azm［11］），as shown in Figs.13 and 14.

In Figs.13a，b and 14a，b，the triangular points denote the results of Williams and Abul-Azm［11］，the solid lines denotetheresultsofthisstudythatincludeevanescentmodes，and the dashed lines denote the results of this study without evanescent modes.refers to the real/imaginary partof the hydrodynamic force in the k-direction on cylinder i due to oscillation in the s-mode of cylinder j.

Fig.12 Test case results.a Oscillation modes of surge and pitch.b h/d of 0.1 and 0.6.c Oscillation modes of surge and pitch，h/d of 0.1 and 0.6

Fig.13 Comparisons ofhydrodynamic coefficients on cylinder1 between the presentstudy（including and withoutevanescentmodes）and Williams and Abul-Azm［11］，L=3a.a Added mass.b Damping coefficients

We can see that the results without evanescent modes are in good agreement with those of Williams and Abul-Azm［11］，which are based on a large-spacing approximation. For the damping coefficient，the two sets of results（including and without evanescent modes）in this study nearly coincide with each other.However，there are evident differences in the solutions of added mass for results including or without evanescent modes，especially for added mass on cylinder 2，which reveals the effects of evanescent modes.

6.1.2Array consisting of five circular cylinders:four in a straight line，the other on a perpendicular bisector of the line

Next，we investigated a cylinder array consisting of five truncated circularcylinders with a specialgeometry configuration，as shown in Fig.15.The configuration of the cylinder array is symmetric about the x-axis.The shaded and hollow circles in Fig.15 denote oscillating and fixed cylinders，respectively.

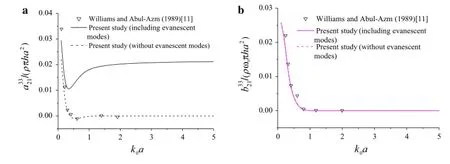
Fig.14 Comparisonsofhydrodynamic coefficientson cylinder2 between the presentstudy（including and withoutevanescentmodes）and Williams and Abul-Azm［11］L=3a.a Added mass.b Damping coefficients

Fig.15 Geometric configuration of cylinders and oscillation forms: cylinder 1 oscillates while others remain still

In Fig.15，we see thatcylinder 1 oscillates in surge，heave or pitch mode，and the others remain still.We calculated the hydrodynamic coefficients of cylinders 1 and 3，including and without evanescent modes，with a water depth d= 20a，draught h=10a，and column spacings L=2.4a，3a，5a.The results are shown in Figs.16-21，where“cylinder 1/3-x/z/pitch-direction（cylinder 1 surge/heave/pitch and 2，3，4，5 fixed）”represents the hydrodynamic coefficients of cylinder 1/3 in the x/z/pitch-direction as cylinder 1 oscillates in surge/heave/pitch mode while othercylinders remain still.

In Figs.16-21，the solid and hollow symbols，respectively，representthe two setsofresults（including and without evanescent modes）for the hydrodynamic coefficients of cylinder 1 or 3 for the configurations shown in Fig.15 with column spacings L=2.4a，3a，and 5a.Figures 16a，b and 17a，b，respectively，show the added mass and damping coefficients of cylinders 1 and 3 in the x-direction as cylinder 1 oscillates in surge mode.Figures 18a，b and 19a，b，respectively，show the added mass and damping coefficients of cylinders 1 and 3 in the z-direction as cylinder 1 oscillates in heave mode.Figures 20a，b and 21a，b，respectively，show the added mass and damping coefficients of cylinders 1 and 3 in the pitch-direction as cylinder 1 oscillates in pitch mode.

Fig.16 Hydrodynamic coefficients of cylinder 1-x-direction（cylinder 1 surge and 2，3，4，5 fixed）.a Added mass.b Damping coefficients

Fig.17 Hydrodynamic coefficients of cylinder 3-x-direction（cylinder 1 surge and 2，3，4，5 fixed）.a Added mass.b Damping coefficients

Fig.18 Hydrodynamic coefficients of cylinder 1-z-direction（cylinder 1 heave and 2，3，4，5 fixed）.a Added mass.b Damping coefficients

Fig.19 Hydrodynamic coefficients of cylinder 3-z-direction（cylinder 1 heave and 2，3，4，5 fixed）.a Added mass.b Damping coefficients

We can see from Figs.16-21 that there are evident differences between the two sets of solutions for added mass（including or without evanescent modes），especially for cylinder 3.The differences increase with a decrease in column spacing.This reveals the effects of the evanescent modes.When the column spacing is L=2.4a，when the cylinder is oscillating in surge mode，the maximum difference between the two sets ofsolutions forthe added mass for cylinder1 is23%，and the maximum difference forcylinder3 is 147%.Forpitch mode（with the same column spacing），the differences are even greater than those of the surge or heave mode.It appears that the effects of the evanescent modes are more pronounced for cases in which the cylinder oscillates in rotational mode than in translationalmode；and these effects are more significant for a fixed cylinder.When the cylinders are located close together，no matter which oscillation mode is considered，the effect of evanescent modes on the added mass is significant and should not be neglected. However，even if the cylinders are located close together，there is little effect by the evanescent modes on the damping coefficients.

Fig.20 Hydrodynamic coefficients of cylinder 1-pitch-direction（cylinder 1 pitch and 2，3，4，5 fixed）.a Added mass.b Damping coefficients

Fig.21 Hydrodynamic coefficients of cylinder 3-pitch-direction（cylinder 1 pitch and 2，3，4，5 fixed）.a Added mass.b Damping coefficients

6.2Array consisting of six circular cylinders:five arranged at the vertices of a regular pentagon inscribed in a circle and the sixth at the center of the circle Another geometric configuration investigated in this paper is an array of six truncated circular cylinders，five of which are arranged at the vertices of a regular pentagon inscribed in a circle and the sixth at the center of the circle，as shown in Fig.22，with d=20a，h=10a，and L=5a.

For this situation，cylinder 1 oscillates in surge mode，cylinders 2 and 5 in rolland pitch modes，cylinders 3 and 4 in heave mode，and cylinder6 remainsstill.Cylinder2 oscillates in phase（in antiphase）with cylinder 5 in the pitch（roll）-direction.The prescribed amplitudes of the oscillation are

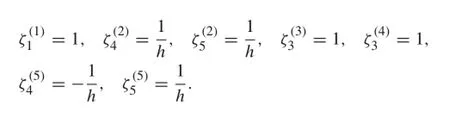
For ζ（j）s，j represents the cylinder number and s the oscillation mode，with j=1，2，3，4，5，and s=1，2，3，4，5.

Fig.22 Geometric configuration of six cylinders

The hydrodynamic pressure distributions on each cylinder at different depths are shown in Fig.23a-f，where A represents wave amplitude.We can see that the pressure distributions of cylinder 2（3）and those of cylinder 5（4）are symmetric with respect to the x-axis because of the symmetry of the geometric configuration and oscillation modes. For the same reason of symmetry，the curves of the pressure distributions on cylinder 1（6）are self-symmetric about the x-axis.

Fig.23 Pressure distributions on each cylinder for oscillation situation in subsection 6.2.a Cylinder 1.b Cylinder 2.c Cylinder 3.d Cylinder 4. e Cylinder 5.f Cylinder 6

7　Conclusions

In this study，we investigated the hydrodynamic interactions ofarrays oftruncated circularcylinders with relative motions（“C2 arrays”）in which each cylinder can oscillate independently in any rigid oscillation mode（including translational and rotational modes，such as surge，sway，heave，pitch，roll，and their combinations）with an arbitrarily prescribed amplitude，including evanescent modes.In addition，we used the orthogonal test method to investigate the effects of several factors influencing convergence in different combinations，and assessed the significances of these different factors.The results illustrate the effects of evanescent modes on hydrodynamic coefficients.Our conclusions are summarized as follows

（1）The calculation results reveal that in the hydrodynamic features of an array of cylinders，as each cylinder oscillates in various modes，there are significant differences in values and variation rules.It appears that the effects of evanescent modes are more pronounced for cases in which the cylinder oscillates in rotational mode than those that oscillate in translational mode；such effects are more pronounced for the fixed cylinder in the array. When the cylinders are located in close proximity，no matter which oscillation mode is considered，the effect ofthe evanescentmodes on the added mass is significant and should not be neglected.However，even if the cylinders are located in close proximity，there is little effect of the evanescent modes on the damping coefficients.

（2）We employed the orthogonal test method in this study，which can dramatically reduce the number of required tests，and we obtain the relationships between different influential factors and convergence behaviors for different factor combinations.The main results can be summarized as follows:the oscillation mode and draught-to-water depth ratio have more significant effects on the convergence rate than wave number and column spacing do；the convergence rates of cases in surge or sway mode are faster than those in heave and rotational modes；the convergence rate increases with a rise in the draught-to-water-depth ratio.The above resultscan play an importantrole in improving efficiency in obtaining convergentresults when analyzing arrays of circular cylinders in various arrangements and oscillation modes.

Acknowledgments The project was supported by the National Natural Science Foundation of China（Grants 11072246，51490673）and the National Basic Research Program（973 Program）of China（Grant 2014CB046801）.

Appendix

The unknown radiation coefficientscan be solved from the equation set

The expressions of the known coefficients in Eq.（A1a，A1b）are

The diffraction transfer matrices of the truncated single cylindersare obtained following the proceduregiven in Kagemoto and Yue［12］，the elements of（or）are the amplitude ofthe q-th（or p-th）partialwave ofthe diffraction potential due to a single unit-amplitude incidence of mode n on cylinder j，which are listed below

The element Tij（n，m，l）in Eq.（A7d）is as follows

1.Falcão，A.F.O.:Wave energy utilization:A review of the technologies.Renew.Sustain.Energy Rev.14，899-918（2010）

2.Eriksson，M.，Waters，R.，Svensson，O.，et al.:Wave power absorption:Experiments in open sea and simulation.J.Appl.Phys.102，084910（2007）

3.Dong，Y.-Q.:Wave Loads and Response of the Oil-extraction Platform in Deep Ocean.Tianjin University Press，Tianjin（2005）（in Chinese）

4.Zeng，X.-H.，Li，X.-W.，Liu，Y.，etal.:Nonlineardynamic responses oftension leg platform with slack-tauttether.China Ocean Eng.23，37-48（2009）

5.Zeng，X.-H.，Shen，X.-P.，Wu，Y.-X.:Governing equations and numerical solutions of tension leg platform with finite amplitude motion.Appl.Math.Mech.Engl.Edition 28，37-49（2007）

6.Zeng，X.-H.，Yu，Y.，Zhang，L.，et al.:A new energy-absorbing device formotion suppression in deep-sea floating platforms.Energies 8，111-132（2015）

7.Wang，C.-Z.，Mitra，S.，Huang，H.-C.，etal.:Finite elementanalysis of second order wave radiation by a group of cylinders in the time domain.J.Hydrodyn.25，348-361（2013）

8.Zhou，B.-Z.，Ning，D.-Z.，Teng，B.，et al.:Fully nonlinear modeling of radiated waves generated by floating flared structures.Acta Mech.Sin.30，667-680（2014）

9.Babarit，A.:Impact of long separating distances on the energy production of two interacting wave energy converters.Ocean Eng.37，718-729（2010）

10.Williams，A.N.，Demirbilek，Z.:Hydrodynamic interactions in floating cylinder arrays-I:Wave scattering.Ocean Eng.15，549-583（1988）

11.Williams，A.N.，Abul-Azm，A.G.:Hydrodynamic interactions in floating cylinder arrays-II:Wave radiation.Ocean Eng.16，217-263（1989）

12.Kagemoto，H.，Yue，D.K.P.:Interactions among multiple threedimensional bodies in water waves:an exact algebraic method.J. Fluid Mech.166，189-209（1986）

13.Linton，C.M.，Evans，D.V.:The interaction of waves with arrays of vertical circular cylinders.J.Fluid Mech.215，549-569（1990）

14.Yilmaz，O.:Hydrodynamic interactions of waves with group of truncated vertical cylinders.J.Waterw.Port Coast.Ocean Eng. 124，272-279（1998）

15.Siddorn，P.，Eatock Taylor，R.:Diffraction and independent radiation by an array of floating cylinders.Ocean Eng.35，1289-1303（2008）

16.Chatjigeorgiou，I.K.:The hydrodynamics of arrays of truncated elliptical cylinders.Eur.J.Mech.B/Fluids.37，153-164（2013）

17.Rao，C.R.:Factorial experiments derivable from combinatorial arrangements of arrays.R.Stat.Soc.（Suppl.）9，128-139（1947）

18.Taguchi，G.:Performance analysis design.Int.J.Prod.Res.16，521-530（1978）

19.The Orthogonal Test Method Authoring Group:Orthogonal Test Method.National Defence Industry Press，Beijing（1976）

20.Fang，K.-T.，Ma，C.-X.:Orthogonal and Uniform Test Design.Sciense Press，Beijing（2001）

21.Hedayat，A.S.，Sloane，N.J.A.，Stufken，J.:OrthogonalArrays:Theory and Application.Springer，New York（1999）

22.Azouzi，R.，Guillot，M.:On-line prediction of surface finish and dimensionaldeviation in turning using neuralnetwork based sensor fusion.Int.J.Mach.Tools Manuf.37，1201-1217（1997）

23.Green，P.E.，Krieger，A.M.，Wind，Y.:Thirty yearsofconjointanalysis:reflections and prospects.Interfaces 31，56-73（2001）

24.Lee，K.H.，Yi，J.W.，Park，J.S.，et al.:An optimization algorithm using orthogonal arrays in discrete design space for structures. Finite Elem.Anal.Des.40，121-135（2003）

25.Wang，T.，Zhou，X.-Q.，Tian，S.-B.，et al.:Numerical simulation method for rock natural stress field of a valley and its application based on orthogonal experiments.Rock Soil Mech.24，831-835（2003）

26.Ali，M.T.，Khalil，G.M.:On hydrodynamic interaction between several freely floating vertical cylinders in waves，In:Proceeding of the 24th International Conference on Offshore Mechanics and Arctic Engineering（2005）

27.Yilmaz，O.，Incecik，A.，Barltrop，N.:Wave enhancement due to blockage in semisubmersible and TLP structures.Ocean Eng.28，471-490（2001）

7 September 2015/Revised:29 January 2016/Accepted:10 March 2016/Published online:20 July 2016

©The Chinese Society of Theoretical and Applied Mechanics；Institute of Mechanics，Chinese Academy of Sciences and Springer-Verlag Berlin Heidelberg 2016