基于拉格朗日下界求解的炼钢-连铸生产调度方法

韩大勇，唐秋华，张利平，张启敏，2

（1.武汉科技大学机械自动化学院，湖北武汉，430081；2.武汉钢铁集团鄂城钢铁有限责任公司，湖北鄂州，436002）

基于拉格朗日下界求解的炼钢-连铸生产调度方法

韩大勇1，唐秋华1，张利平1，张启敏1，2

（1.武汉科技大学机械自动化学院，湖北武汉，430081；2.武汉钢铁集团鄂城钢铁有限责任公司，湖北鄂州，436002）

为提高炼钢-连铸生产效率，以加权总完工时间、作业等待惩罚总和最小化为目标，基于时间索引建立数学规划模型。在证明原问题、松弛问题、对偶问题三者最优解关系基础上，将机器容量约束松弛到目标函数中，运用次梯度算法求原问题下界，得到各炉次的开始时间序列。为消除松弛解中的有向环，采用融入启发式规则的列表调度，按照机器可用性优先原则，将炉次均衡地指派到各个加工机器上。利用GAMS/Cplex软件对18个调度算例进行测试运算，结果表明以较少的计算代价可以得到令人满意的近优解，因此本文提出的基于拉格朗日下界求解的方法对炼钢-连铸生产调度问题是可行的和有效的。

炼钢-连铸；生产调度；拉格朗日松弛算法；对偶问题；次梯度方法；启发式规则

钢铁生产系统涉及因素多、工序复杂，而炼钢-连铸过程是其中的关键环节之一。该生产过程包括一组有序的作业，每一个作业都需要按照一定的操作顺序经历三个主要生产阶段，即炼钢、精炼和连铸，并且每个作业都有规定的操作时间和优先级。从生产管理的角度来看，炼钢-连铸阶段的主要特点为:在生产过程中钢水需要保持在一定温度以上；在连铸阶段必须按浇次进行成批连续加工；需要考虑工件的运输时间、连铸和热轧工序之间的紧密衔接。考虑上述特点，可把炼钢-连铸生产调度视为具有工件（即炉次）驻留时间受限、最后阶段成批连续加工（即连浇连铸）、准时完工等特殊要求的混合流水车间调度问题。

围绕炼钢-连铸生产调度问题，已有研究主要分为三大类:智能算法、启发式算法、基于数学规划的精确算法和近似算法。Atighehchian等［1］通过蚁群算法进行炉次指派和排序，形成粗调度方案，再利用非线性规划求解算法消除粗调度中的设备冲突，形成可行调度方案。该方法计算效率较高，可面向实际应用，但当第一阶段产生的粗调度不够理想时，第二阶段的优化空间就有限。刘光航等［2］提出一个基于混合整数规划模型的设备冲突解消启发式方法，利用最优线性规划来求解。Tang等［3-4］采用以拉格朗日松弛法为基础的近似算法求解炼钢-连铸生产调度整数规划模型，该方法通过对时间变量均匀离散化来建立近似模型，提高了求解效率。

根据计算复杂性理论，大多数调度问题都属于NP难问题，而炼钢-连铸调度问题更是一种特殊的混合流水车间调度问题，使用精确的求解算法和全局优化算法（如分支定界法）在多项式时间范围内很难求得最优解。相反，研究近似算法或针对具体问题的特殊性调度方案更具有现实意义。事实上，很多调度问题存在特殊的数学结构，若能有效利用，可极大降低求解的计算复杂度。拉格朗日松弛算法针对一些具有可分解性的特殊结构，通过对难约束松弛以及对松弛问题分解，将原问题转化为较易处理的子问题或局部问题。基于拉格朗日松弛原理，Tanaka等［5］提出一种分支定界算法求解并行机调度问题，每个分支的界便是由拉格朗日松弛法生成的下界解。Mellouli等［6］设计一种列生成（column generation）方法，用于解决带有完工时间总加权和的并行机调度问题。Chang等［7］融合拉格朗日松弛和网络流方法求解带有交货期的流水车间调度问题，即首先松弛机器能力约束，然后利用网络流求解松弛问题，最后利用优先因子法构造了一个生成可行解的启发式方法。Nishi等［8］采用切片生成（cut generation）的拉格朗日松弛法求解带有总权重拖期的混合流水车间调度问题，所得拉格朗日下界有很大改善。在现有生产调度优化中求解拉格朗日对偶问题主要采用次梯度算法，但该算法本身有许多不足，主要包括收敛条件过于严格和求解效率低。针对求解效率低的不足，研究人员已提出了多种改进方法，如序列求解［9］、对松弛策略进行调整［10］、引入神经网络算法［11］等；针对收敛条件过于严格的问题，目前主要解决办法是采用最大迭代次数或最大运行时间作为终止条件。

用格朗日松弛算法解决调度问题主要有3个步骤:构造拉格朗日算法模型并进行解耦，更新拉格朗日乘因子，构造可行调度方案。针对炼钢-连铸生产调度问题，在已有拉格朗日松弛问题求解方法的基础上，本文拟着重进行以下两方面的工作:①进一步剖析次梯度算法，研究在拉格朗日子问题求解时影响结果的关键性因素——次梯度的迭代策略；②基于拉格朗日松弛方法所求得的原问题解的下界，构造出较优的可行解生成模型，并用启发式方法完成求解。

1　炼钢-连铸生产调度模型

1.1问题描述

炼钢-连铸生产调度主要涉及炼钢、精炼和连铸三个阶段，如图1所示。炼钢阶段接受来自高炉的铁水，通过转炉或电弧炉将冶炼好的铁水或废钢转换为钢水；炼钢结束后将钢水注入钢包，并转运到精炼设备中进一步调整钢水的温度和成分；精炼后的钢水被运送到指定的连铸机，连浇连铸后形成板坯。在此过程中，运送钢水的每个钢包被称为一个炉次或“工件”，是炼钢-连铸的最小生产单元；在同一台连铸机上连续浇铸的炉次集合被称为一个浇次，是炼钢-连铸的最大生产单元。每个炉次需按照上述工艺顺序依次经过三个阶段，每个阶段可能存在一台或多台并行的生产设备。

图1　炼钢-连铸生产工艺流程Fig.1 Process flow of steelmaking-continuous casting production

假定:①各炉次在每个阶段的处理时间已知；②在调度开始时所有的机器均为可用状态；③同一阶段每台机器性能相同，且不考虑因机器故障所引起的生产中断或停线。

因此，炼钢-连铸生产调度可以描述为:炉次j沿着指定的工艺路线经过i个阶段，每个阶段具有u台相同机器（u≥1），且至少有一个阶段的机器数大于1；在最后一个阶段以浇次为单位连续作业。

1.2模型构造

模型中的符号说明:j表示炉次，j=1，2，…，n；l表示浇次，l=1，2，…，B；i表示加工阶段，i=1，2，…，s；k表示作业的时间点，k=1，2，…，K。

已知参量:bl表示浇次l中的作业总数；mi表示各阶段机器数量；Pij表示作业j在i阶段的处理时间；Sij表示作业j在i阶段中的机器上处理前的机器准备时间；wj表示作业j的权重；rij表示作业j在i阶段完成后的等待时间的惩罚系数；alf表示浇次l中的第f个作业，f=1，2，…，bl。

决策变量:Cij（连续变量），为作业j在阶段i处理的完成时间；δijk（0-1变量），如果炉次j在时间点k时位于阶段i进行处理，则δijk=1，否则δijk=0。

目标函数（包含两部分）:第一部分是总加权完成时间，以控制生产效率；第二部分为总拖期或提前惩罚，以保证准时交货。

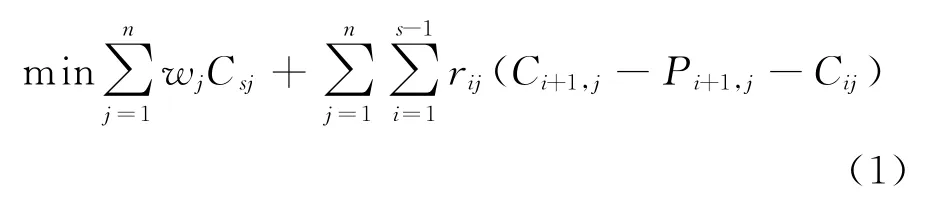
机器能力约束:同一时刻在i阶段上加工的炉次总数不大于i阶段上的机器数；同一炉次j必须在前一阶段完成后才能进入下一阶段。

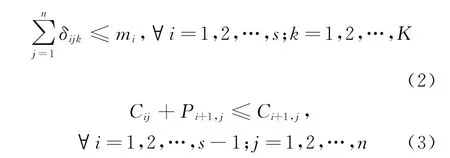
浇次连铸工艺约束:在最后一个阶段，同一浇次内各炉次需按照事先给定的炉次顺序连续无间断地加工。

机器加工无中断约束:如果炉次j被分配在事件点k加工，直到炉次j被加工完，机器才能停工。

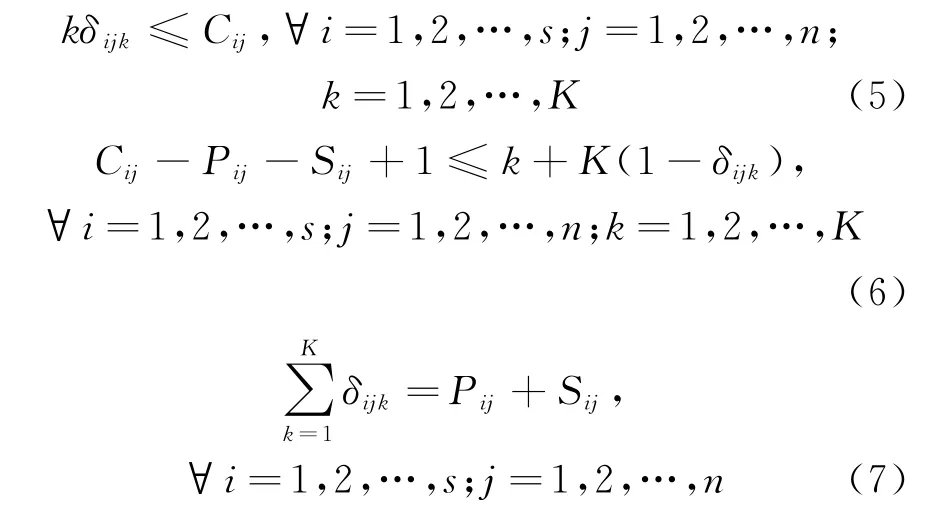
联立式（1）～式（7）即可形成炼钢-连铸生产调度数学模型。

2　拉格朗日下界求解

由前面的分析可知，以炼钢-连铸实际生产为基础所构造的混合整数规划模型难以求解。为简化模型求解同时又要获得最优解，这里引入拉格朗日松弛算法。具体策略是:将模型中的难约束松弛为目标函数的一部分，减少原问题约束条件，构造其对偶问题并进行求解。这里求得的解为原问题解的下界，利用拉格朗日松弛求取该下界的方法称为拉格朗日下界求解。

2.1拉格朗日对偶解的较优性分析

由于约束条件松弛，原问题的属性被改变，解空间增大，所求拉格朗日松弛问题的最优解不一定是原问题的最优解，在原问题中甚至不一定可行。

为更好地接近原问题的最优解，常用拉格朗日对偶问题的对偶解来代替拉格朗日松弛问题的解。以下利用对偶理论相关知识，对拉格朗日对偶问题的解的优越性进行论述和证明。

假定线性规划问题（IP）的简化形式为:

可得到其对应的松弛问题（LP）:

以及对偶问题（LD）:

引理 若混合整数线性规划松弛问题存在可行解，则有ZLP≤ZLD≤ZIP。

证明:混合整数线性规划问题的解集是有限的离散点的集合，记为Q=｛x|Bx≤d，x∈Z+｝，可验证凸包Con（Q）为凸集。

由

得到

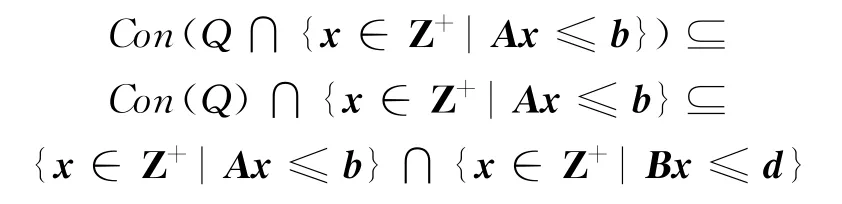
若拉格朗日对偶问题的目标值ZLD有界，则:

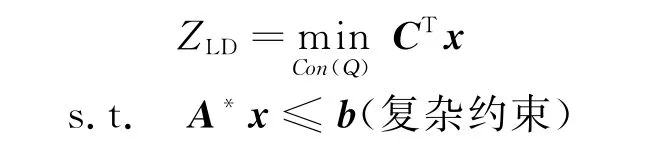
即ZLD=min｛CTx|Ax≤b，x∈Con（Q）｝。

所以有:ZLP≤ZLD≤ZIP。证毕。

上述逻辑关系还可进一步用图2表示。由此可以判断，为找到与原问题解更为接近的解，可在拉格朗日松弛基础上，进一步进行拉格朗日对偶转化。

图2　原问题解、松弛解与对偶解的关系Fig.2 Relationship between original solution，relaxation solution and dual solution

2.2拉格朗日松弛

在传统松弛法框架下，可以充分利用问题结构特征对不容易处理的约束引入拉格朗日乘子进行松弛，使其在应用时有很大的灵活性，能够适应复杂多变的约束类型。这里引入非负的拉格朗日乘子μ，将资源析取约束式（2）松弛到目标函数，得到拉格朗日松弛问 题（LR）的目标函数，如式（8）所示。

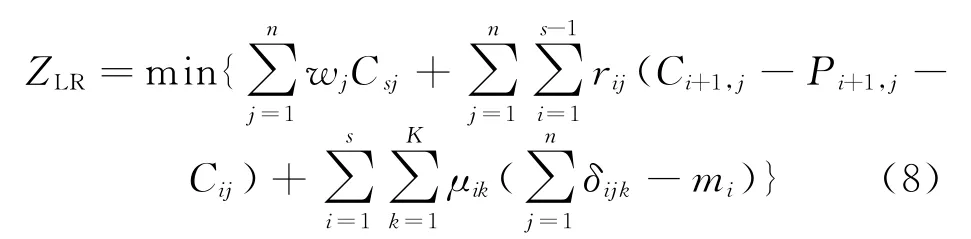
拉格朗日乘子非负约束:

联立式（3）～式（6）、式（8）～式（9），共同形成拉格朗日松弛问题。

由式（8）及其所包含的变量和参数性质不难看出，ZLR可以分解为含未知变量的部分ZLR1以及常量部分ZLR2，即

其中

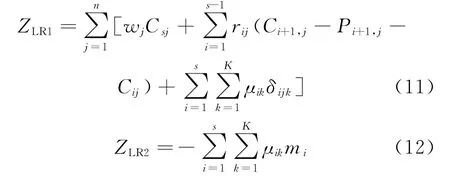
2.3拉格朗日对偶

将拉格朗日松弛问题视作原问题，且其最优化方向为最小化，根据对偶定理，其对偶问题则为最大化问题，相应的目标函数为:

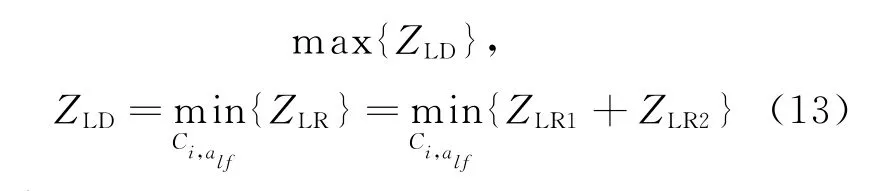
到此为止，在拉格朗日松弛算法的架构下，将原来的炼钢-连铸调度问题转化成较易处理的对偶问题。通过数学结构特征分析可知，在此模型中耦合了所有浇次的机器能力约束松弛。为使问题易于求解，松弛约束式（2），解除浇次之间的耦合关系。将松弛问题划分成一组独立的容易求解的浇次级子问题，每一个子问题对应一个浇次。因而在求解时主要考虑的是单个浇次和独立浇次内的调度子问题。在各子问题间以及子问题与原问题间起协调作用的是拉格朗日乘子。

从式（10）可以看到，等式右边包含两部分，对于任一给定的拉格朗日乘子，第二项为常数，第一项是对所有浇次的求和。而且，式（3）～式（6）都正好对应一个浇次内的炉次约束，因此LD问题是可以被分解为浇次级子问题的。以第l个子问题为例:

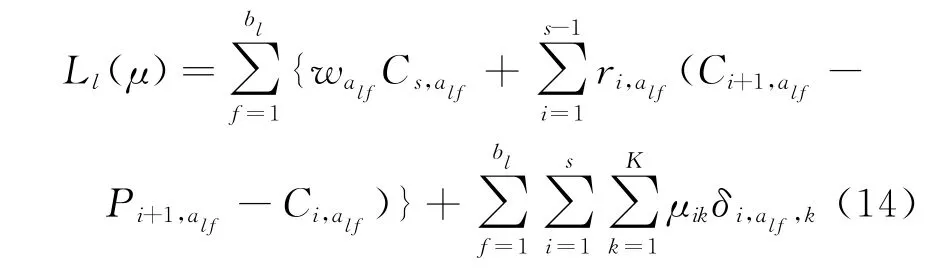
于是，LD问题可转化为:

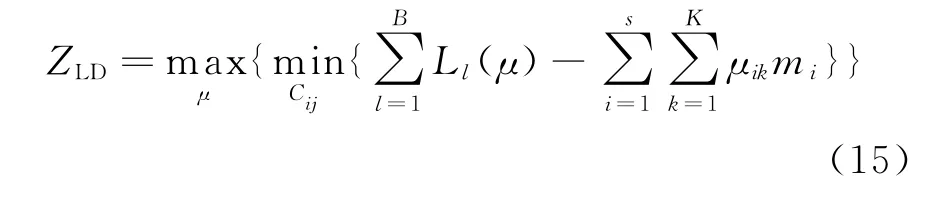
2.4次梯度算法更新拉格朗日乘子

次梯度算法是求解对偶问题较为有效的方法，其与非线性规划梯度下降的思想相同。拉格朗日对偶问题是希望松弛问题的下界尽可能大，于是可按照松弛下界的上升方向逐渐逼近对偶问题的最优上界值。

由连续函数的性质，可以推导并证明在其极点处的超平面方程，即

式中:gik表示次梯度。

采用次梯度算法更新拉格朗日乘子的基本思路是:对给定的拉格朗日乘子，分别计算出松弛解和次梯度的值，并判断松弛解的最优性，如果不满足条件则以这个次梯度方向为上升方向寻求松弛解上界。次梯度算法具体步骤如下:

步骤1 任意选择一个初始拉格朗日乘子μ1，令h=1。

步骤2 对μh，计算其次梯度gh。若满足迭代终止原则，则认为获得最优解，停止迭代，否则按照下面的迭代法则更新拉格朗日乘子μh。

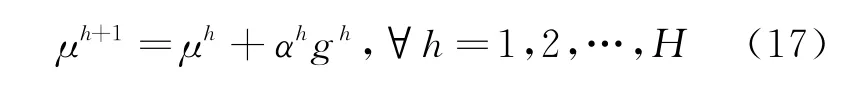
式中:αh为迭代的步长；H为最大迭代次数。

式中:λ为调整系数，0＜λ＜2，一般根据经验取值；L*为当前所能得到的最好解；Lh为每次迭代之后的实际值。

迭代终止原则为:

（1）gh=0，这是理论上的最理想状态。

（2）在实际问题中，还可以设置最大迭代次数H。

（3）对拉格朗日乘子和松弛解按变化率设置条件。在连续多次迭代中，如果拉格朗日乘子或松弛解的变化率ε小于给定的某一趋于0的值，可认为取得最优解。

针对不同的问题，根据计算的方便和条件特殊性等约束，可以选择以上任意一种迭代终止条件，或者综合运用。本文选择迭代终止原则（3），即在迭代过程中，当LR实际值的变化率小于一个预先设定的较小的正整数ε时，就认为近似取得最优解。

3　基于拉格朗日下界的可行解生成方法

3.1可行解生成问题分析

在拉格朗日松弛算法框架下求解对偶问题，可获得炉次的机器分配结果。然而，由于松弛了机器容量约束，导致不同炉次在同一台设备上加工有可能冲突，即同一台设备上的所有炉次加工顺序之间可能会出现有向环。

例如，松弛解有可能出现如下情况:对于在第1阶段的3个加工炉次（炉次1、2、3），其指派变量的解为炉次1、2和3安排在机器1上，顺序变量的解为炉次1先于炉次2加工、炉次2先于炉次3加工和炉次3先于炉次1加工。此情形下的加工顺序明显出现矛盾。

上述问题被简称为列表调度问题。为了消除有向环，可通过前一阶段的顺序变量确定所有炉次的加工顺序；然后按照机器优先可用性原则，将炉次均衡地指派到各个加工机器上，确定每个阶段每个炉次的加工设备以及每炉次在各个阶段的开始加工时间。

3.2基于混合整数线性规划的可行解构造模型

针对炼钢-连铸生产调度问题，大多数数学建模方法是采用大M法或析取规划方法。其中，大M法采用一个足够大的常数（通常是生产周期）来表示设备能力极限约束，即多个工件不能同时在一台设备上加工。该方法简单易懂，但其数值大小直接影响求解过程的稳定性，而且其松弛解的质量较差。基于析取规划的数学建模方法［12］可避免上述数值计算问题，但对设备能力约束的表示较为复杂，同时也增加了求解的难度。

根据采用拉格朗日下界求解方法得到的顺序变量，可构建如下混合整数线性规划模型，来解决列表调度问题。

符号说明:MAX为一个极大数；决策变量Si，k，t表示阶段i中机器t的第k个任务的开始加工时间；决策变量Zi，j，k，t为0-1变量，如果炉次j在阶段i的机器t上位于时间点k进行处理，则Zi，j，k，t=1，否则Zi，j，k，t=0；yi，j，j′为0-1变量，如果在同一阶段上作业j先于作业j′加工，则yi，j，j′=1，否则yi，j，j′=0。

目标函数:最小化炉次在机器上的处理开始时间，即

机器及炉次分配约束:每个炉次在任一阶段必须且只能分配到一个机器的一个时间点k，即

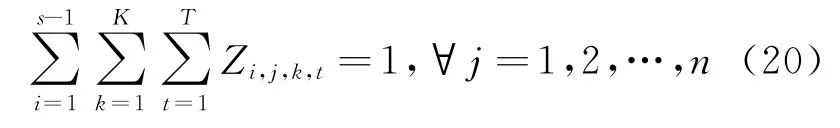
最多有一个炉次被分配到任一机器t的一个时间点，即

当前的时间点不能被分配，除非它前面的时间点已经被分配，即

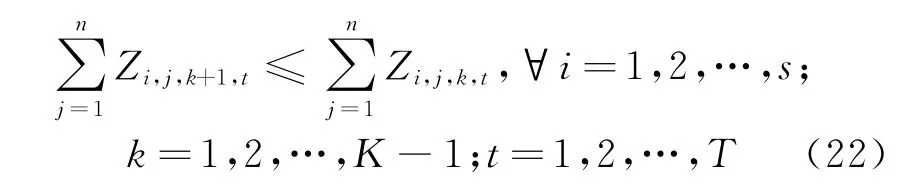
浇次内约束:如果炉次j和j′事先安排为同一浇次内的两个炉次，那么两炉次在最后阶段必须分配在同一个机器上，即

加工连续性约束:如果炉次j被分配到机器t的时间点k，则机器t不能停工直到炉次j被加工完。由于缓冲器有缓冲能力，且存储时间不确定，故以下式（24）和式（25）中的符号“≥”表示了该时间的不确定性。

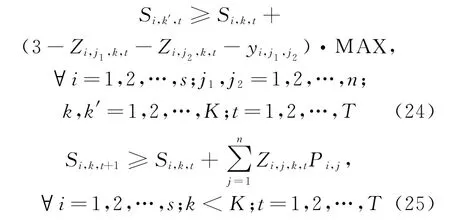
唯一性约束:为消除有向环，同一阶段各炉次的排序必须唯一，即

联立式（19）～式（27）即可构造一个简单的列表调度数学模型，该模型可采用GAMS/Cplex软件进行求解。

3.3可行解启发式快速生成

对于小规模调度问题，采用上述方法可较容易地获得最优可行解，而针对大规模案例时，为了能快速获得最优解，本文提出一个融入列表调度思想的启发式算法。在加工的第一阶段，按照拉格朗日松弛问题解的升序得到一个初始炉次加工序列，基于最早结束优先规则修正第二阶段的解，同时进行机器分配，依此类推，得到连铸阶段的炉次加工序列和机器分配。该算法的具体步骤如下:

步骤1 由拉格朗日松弛解可得到每个加工炉次在阶段i上的开始时间sti，j，作为一个初始列表。

步骤2 依据初始列表，将所有元素按升序排列，确定每个阶段i上的工作排序Ti。

步骤3 Ti（m）表示Ti中的第m个元素，令j=argj∈Ω｛sti，j=stTi（m），j｝，其中Ω表示作业集合，更新机器t的所有分配炉次集合，所分配炉次数加1。

步骤4 如果m≤n，转至步骤3；否则，令i=i+1，转至步骤5。

步骤5 如果i＜s，返回步骤2；否则，转至步骤6。

步骤6 输出机器指派变量值。

4　算例分析

4.1实验数据

利用GAMS 23.8/Cplex软件对上述拉格朗日算法进行编程，并在Intel（R）Core（TM）i3-2120 CPU@3.30 GHz主频、4 GB内存、Windows 7/32位操作系统环境下运行。将最大迭代数50设为停止条件。针对每种问题规模随机产生几组不同数据，利用这些下界数据的平均性能来验证算法求解的有效性。

虽然本文算法能求解不同阶段有不同机器数的调度问题，但为了简化实验数据，这里假设每阶段的机器数均为2（3个阶段共6台机器），并随机产生炉次总数s∈｛4，8，12，18，24，30，36，40，48｝、浇次总数bl∈｛2，3，4，5，6，8｝，工件权重设置相同且为1。

针对不同参数的组合随机产生18个算例，如表1所示，表中同时列出经过多次迭代后得到的拉格朗日下界。

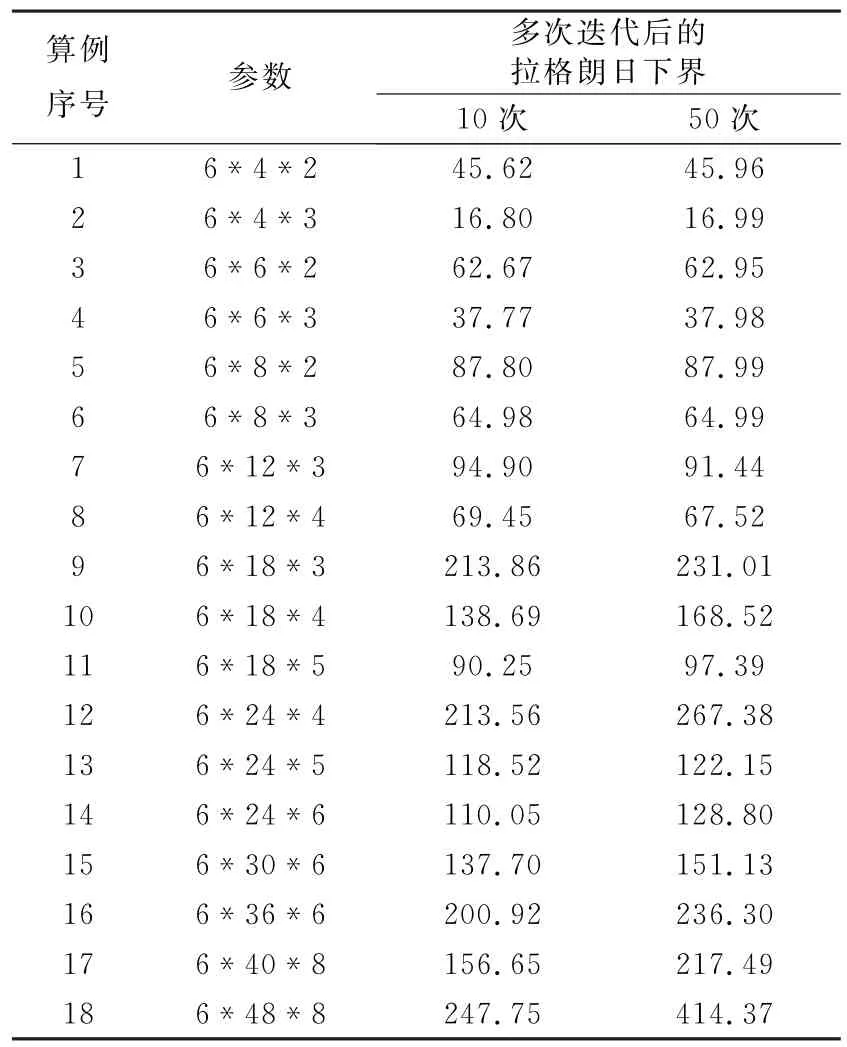
表1　实验数据Table 1 Experimental data

4.2解的有效性分析

以包含三个浇次的简单算例（算例2）为代表，进一步完成可行解的构造，其中三个浇次｛1，2，3｝分别包含有炉次｛1，2｝，｛3｝，｛4｝。表2列出了每个炉次在三个阶段的处理时间，各炉次的加权惩罚系数w均为1。在拉格朗日松弛问题的求解基础上利用启发式方法构造可行解，得到可行方案的甘特图，如图3所示。

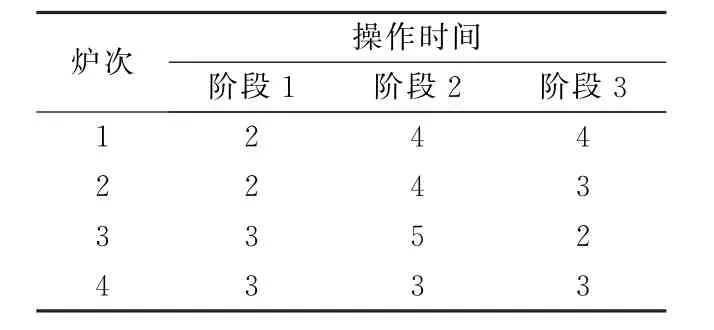
表2　各炉次在不同阶段的操作时间Table 2 Operation times of all furnaces at different stages

图3　可行方案的甘特图Fig.3 Gantt chart of the feasible scheme

由GAMS23.8/Cplex程序运行情况可知，该问题一共产生了141个离散变量、30个连续变量、3775个线性方程，通过10次迭次获得最优解（图3）。该结果表明，利用拉格朗日启发式算法可以获得较好的解甚至最优解。

4.3拉格朗日下界分析

从计算所得到的拉格朗日下界（见表1）来看，每个浇次内预先设定的炉次分配对问题的下界有较大影响。如表1中的算例7和算例8，针对相同的炉次数（12）和机器数（6），算例7采取3浇次，算例8采用4浇次，结果得到的拉格朗日下界有很大区别，其中浇次数较小的案例所得下界值较优。同时，算法中炉次数和浇次数等参数值较大时，会影响算法的收敛性，使得对偶问题很难收敛到最优值。

另外，从程序的运行时间和迭代次数来看，结合次梯度优化的拉格朗日松弛算法在迭代前期收敛速度较快，但随着迭代次数的增加，收敛速度会有所减缓。

5　结语

本文建立了炼钢-连铸生产调度的0-1整数规划模型，求解时将非线性的目标函数转化成线性的，通过松弛资源析取约束来解除连续变量和整数变量之间的耦合关系，将松弛问题分解成两个容易求解的子问题。在构造问题的可行解时基于传统的启发式思想，建立新的混合整数线性规划列表调度模型，并利用GAMS/Cplex软件求解得到较优解。进一步的研究将重点考虑在更短时间内取得更大规模问题的下界，以提高算法的求解效率。

［1］Atighehchian A，Bijari M，Tarkesh H.A novel hybrid algorithm for scheduling steel-making continuous casting production［J］.Computers and Operations Research，2009，36:2450-2461.

［2］刘光航，李铁克.炼钢-连铸生产调度模型及启发式算法［J］.系统工程，2002，20（6）:44-48.

［3］Tang Lixin，Luh P B，Liu Jiyin，et al.Steel-making process scheduling using Lagrangian relaxation［J］.International Journal of Production Research，2002，40（1）:55-70.

［4］Tang Lixin，Liu Jiyin，Rong Aiying，et al.A mathematical programming model for scheduling steelmaking-continuous casting production［J］.European Journal of Operational Research，2000，120: 423-435.

［5］Tanaka S，Araki M.A branch-and-bound algorithm with Lagrangian relaxation to minimize total tardiness on identical parallel machines［J］.International Journal of Production Economics，2008，113:446-458.

［6］Mellouli R，Kacem I，Sadfi C，et al.Lagrangian relaxation and column generation-based lower bounds for the Pm，hj1scheduling problem［J］. Applied Mathematics and Computation，2013，219: 10783-10805.

［7］Chang S-C，Liao D-Y，Hsieh F-S，et al.Flow shop scheduling by a Lagrangian relaxation and network flow approach［C］//Proceedings of the 29th IEEE Conference on Decision and Control.Honolulu，Hawail，1990:122-124.

［8］Nishi T，Hiranaka Y，Inuiguchi M.Lagrangian relaxation with cut generation for hybrid flowshop scheduling problems to minimize the total weighted tardiness［J］.Computers and Operations Research，2010，37:189-198.

［9］Chen Haoxun.A sequential Lagrangian relaxation approach to job shop scheduling［J］.控制理论与应用，1995，12（6）:752-757.

［10］Chen Haoxun，Chu Chengbin，Proth J-M.An improvement of the Lagrangean relaxation approach for job shop scheduling:a dynamic programming method［J］.IEEE Transactions on Robotics and Automation，1998，14（5）:786-795.

［11］Luh P B，Zhao Xing，Wang Yajun，et al.Lagrangian relaxation neural networks for job shop scheduling［J］.IEEE Transactions on Robotics and Automation，2000，16（1）:78-88.

［12］Xuan Hua，Tang Lixin.Scheduling a hybrid flowshop with batch production at the last stage［J］. Computers and Operations Research，2007，34: 2718-2733.

［责任编辑 尚 晶］

Lagrangian lower bound solution based method for steelmaking-continuous casting production scheduling

Han Dayong1，Tang Qiuhua1，Zhang Liping1，Zhang Qimin1，2
（1.College of Machinery and Automation，Wuhan University of Science and Technology，Wuhan 430081，China；2.Echeng Iron and Steel Co.，Ltd.，Wuhan Iron and Steel Corporation，Ezhou 436002，China）

To improve the production efficiency of steelmaking-continuous casting，a mathematical programming model is established based on time index with the objective of minimizing the sum of weighted completion time and waiting punishment.with the relationship between the optimal solutions of original problem，relaxation problem and dual problem proved，the machine capacity constraints are relaxed to the objective function，and the sub-gradient method is employed to seek the lower bound of the original problem，then the start time sequence of all ladles is obtained.To eliminate the directional ring in the relaxation solution，a list scheduling method integrated with heuristic rules is used and all ladles are evenly assigned to the machines according to the priority principle of machine availability.Eighteen scheduling examples are calculated by GAMS/Cplex software.The results show that satisfactory near optimal solution can be achieved at less computing cost.So the proposed method based on Lagrangian lower bound solution is feasible and effective to solve the steelmaking-continuous casting production scheduling problem.

steelmaking-continuous casting；production scheduling；Lagrangian relaxation algorithm；dual problem；sub-gradient method；heuristic rule

TF087；TP29

A

1674-3644（2016）05-0353-08

2016-04-06

国家自然科学基金资助项目（51275366，51305311）；中国博士后科学基金资助项目（2013M542073）；高等学校博士学科点专项科研基金课题（博导类）（20134219110002）.

韩大勇（1990-），男，武汉科技大学硕士生.E-mail:1223408932@qq.com

唐秋华（1970-），女，武汉科技大学教授，博士生导师.E-mail:tangqiuhua@wust.edu.cn